深度优先搜索(dfs)题目合集
深度优先搜索(dfs)题目合集
- 全排列问题 dfs原理和模版
- 深度优先搜索原理(纯个人理解)
- 参考程序
- dfs通用模版
- 素数环
- 组合的输出 剪枝+新dfs模版
- 参考程序
- 新的dfs模版
- 自然数的拆分 利用形参进行回溯
全排列问题 dfs原理和模版
P1706 全排列问题 - 洛谷 | 计算机科学教育新生态
深度优先搜索原理(纯个人理解)
和循环做对比:
两层循环嵌套的情况下,假设内层循环运行到一半时我不想运行了,我想把外层循环的状态往回拨(例如for循环一般用一个进度标记变量i表示循环进度,修改i的值用以控制循环)重新开始。
但是直接终止内层循环的话,即使修改外层循环的循环进度,也无法回到外层循环之前的状态,或者说需要付出巨大的条件。
我们知道,递归是函数调用自己本身。底层有专门的寄存器记录当前函数的进度,当函数递归时,在函数所在的栈空间会生成一个和自己一样的函数先执行,新生成的函数执行完了,会回到原来的函数原来的进度继续进行。
利用这个特性,我们用递归代替外层的循环,内部再用一个循环,这样内层循环运行到一半不想运行了,直接退出当前函数,回到上一层函数发生递归的语句后,继续运行。这样做的最大好处是可以以非常低的成本回到之前的状态。
这种利用递归和栈的特性实现的枚举方式被称作**深度优先搜索(depth first search,简称dfs)**算法。
例如这题枚举全排列,假设枚举到1,2,3时,输出123,然后3的空位让出来,3后面没有数字了,回到2,2的后面还有一个3,于是有了1,3;再到第三个空位,此时有1,2可以用,1之前用过了,就把2放上去,于是就有了132。
利用这个思路,即可完成全排列的枚举。而这个思路也是dfs的通用思路。
用这个算法时一定要想清楚状态,以及回来(书上和资料上叫回溯)的时候,哪些状态要还原,哪些不还原。例如这里1之前用过了,后面就不能用了,等之前的用完了才能用。
参考程序
#include<stdio.h>int flag[10];
int ans[10],p;//深度优先搜索
void dfs(int n,int depth){if(depth>n){int i=0;for(i=1;i<=n;i++){printf("%5d",ans[i]);}printf("\n");return;}int i=1;for(i=1;i<=n;i++){if(flag[i]==1)continue;flag[i]=1;//标记状态,下层枚举时跳过这层 ans[++p]=i;//记录答案 dfs(n,depth+1);//前往下一层 --p;//回溯 flag[i]=0;//回到之前的状态}
}int main() {int n;scanf("%d",&n);dfs(n,1);return 0;
}
但这个算法的时间复杂度一般都是平方甚至是指数级,若递归太深还会导致栈溢出。所以dfs也有很大的局限性。为了降低复杂度和减少栈溢出,有很多技巧(有的大佬称之为剪枝)可以进行,后面有刷到相关的题就提一下。
dfs通用模版
模拟两层循环的dfs模版:
void dfs(int depth, 其他参数){//depth用于标记递归深度,可以没有if(depth太深不给往下走了或其他情况){整理状态;return;}if(其他情况(如果有的话,虽然可以放在一个if里处理)){整理状态;return;}//...for(初始情况;是否枚举完了所有情况;){if(情况1不符合条件)continue;if(情况2不符合条件)continue;//...标记状态;处理当前情况;dfs(depth+1,其他参数);将标记的状态回溯到原来的样子;}
}
个人更喜欢用这个,因为在比赛的环境下,自己并不能一下子想到所有不符合条件的情况或状态,所以用这个模版的话想到一个添加一个,也不用修改之前的判断。
当然,模版并不唯一,只要能理解整个思路,以及整理好实际问题的所有状态,就能用dfs解决问题。
素数环
2110:【例5.1】素数环
参考程序:
#define _CRT_SECURE_NO_WARNINGS 1/*
http://ybt.ssoier.cn:8088/problem_show.php?pid=2110
*/#include<iostream>
#include<cmath>
#define endl "\n"
using namespace std;bool flag[31] = { 0 };
int n = 0;
int ans[31] = { 0 };//数据范围不超过30,所以数组开31个空间bool prime(int x) {//判断素数if (x == 2)return true;if (x < 2)return false;int i = 2;while (i <= sqrt(x) && x % i != 0)i++;if (x % i == 0)return false;return true;
}inline int judg(int x) {//防止数据越界if (x > n)return 1;if (x < 1)return n;return x;
}void dfs(int depth) {if (depth == n+1) {//所有空位都填满了flag[0] = true;return;}for (int i = 1; i <= n; i++) {if (flag[i])//这个数字用过continue;//上一个空填有数字,并且i和那个数字的和不是素数if (ans[judg(depth - 1)] != 0 && !prime(i + ans[judg(depth - 1)]))continue;if (ans[judg(depth + 1)] != 0 && !prime(i + ans[judg(depth + 1)]))continue;ans[depth] = i;flag[i] = true;dfs(depth + 1);if (!flag[0]) {//如果凑齐了一个环,就不回溯,等所有递归解除回到main函数flag[i] = false;ans[depth] = 0;}}
}int main()
{cin >> n;dfs(1);for (int i = 1; i <= n; i++)cout << ans[i] << ' ';return 0;
}
组合的输出 剪枝+新dfs模版
1317:【例5.2】组合的输出
剪枝的一个例子。
举1为根结点的树的例子,画红圈的都是不要的结点,应该剪去。

参考程序
剪去结点的方法很多,比如在内层循环中作判断:
#include<iostream>
#include<cstdio>
using namespace std;int n, r, num[101];
bool vis1[101] = { 0 };
void dfs1(int dep)
{if (dep == r + 1){for (int i = 1; i < dep; i++)printf("%3d", num[i]);printf("\n");return;}for (int i = 1; i <= n; i++){if (!vis1[i]&&i>num[dep-1])//这层递归填进去的答案比上一层大{vis1[i] = 1;num[dep] = i;dfs1(dep + 1);vis1[i] = 0;}}
}int main()
{cin >> n >> r;dfs1(1);return 0;
}
或者对内部的循环的枚举范围进行限制:
#include<iostream>
#include<cstdio>
using namespace std;int n, r, num[101];
bool vis1[101] = { 0 };
void dfs1(int dep) {if (dep == r + 1) {for (int i = 1; i < dep; i++)printf("%3d", num[i]);printf("\n");return;}//从上一层的最大数开始枚举,很不错的剪枝 for (int i = num[dep - 1] + 1; i <= n; i++) {if (!vis1[i]) {vis1[i] = 1;num[dep] = i;dfs1(dep + 1);vis1[i] = 0;}}
}int main() {cin >> n >> r;dfs1(1);return 0;
}
可以的话尽量用第2种思路,第2种思路直接规避掉了很多不必要的判断。
新的dfs模版
void dfs(int depth, 其他参数){//depth用于标记递归深度,可以没有if(depth太深不给往下走了或其他情况){整理状态;return;}if(其他情况(如果有的话,虽然可以放在一个if里处理)){整理状态;return;}//...for(初始情况;是否枚举完了所有情况;){if(符合条件){标记状态;处理当前情况;dfs(depth+1,其他参数);将标记的状态回溯到原来的样子;}}
}
自然数的拆分 利用形参进行回溯
1318:【例5.3】自然数的拆分
例如这个样例:
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4
后面输出的数都不比前面的小,又都能保证全部加起来等于7。
所以用到上题的剪枝。
参考程序:
#ifndef _CRT_SECURE_NO_WARNINGS
#define _CRT_SECURE_NO_WARNINGS 1
#endif
#include<iostream>
using namespace std;
int ans[101] = { 0 };
int total = 0;void dfs(int depth, int n, int sum, int ls) {if (sum == 0) {++total;cout << n << "=";for (int i = 1; i < ans[0]; i++)cout << ans[i] << "+";cout << ans[ans[0]] << endl;return;}if (depth > n || sum < 0)return;for (int i = ls; i < n; i++) {ans[++ans[0]] = i;//没有明显的条件限制dfs(depth + 1, n, sum - i, i);--ans[0];//回溯}
}int main() {int n = 0;cin >> n;dfs(1, n, n, 1);return 0;
}
发现参考程序可以进一步被优化。例如n作为全局变量,sum记录枚举的数的和,当递归到下一层时,sum+i作为实参传递给下一层,回来之后,sum还是sum。
因为sum是形参,可以理解为局部变量,局部变量出了自己的作用域就用不了了,而每层递归的形参和上层递归的关系只有上层递归传值给这层递归。利用这个原理,可以实现自动回溯。
#ifndef _CRT_SECURE_NO_WARNINGS
#define _CRT_SECURE_NO_WARNINGS 1
#endif
#include<iostream>
using namespace std;
int ans[101] = { 0 };
int total = 0;
int n = 0;void dfs(int depth, int sum) {if (sum > n)return;if (sum == n) {cout << n << "=";for (int i = 1; i < depth - 1; i++)cout << ans[i] << "+";cout << ans[depth - 1] << endl;return;}for (int i = ans[depth - 1]; i < n; i++) {ans[depth] = i;dfs(depth + 1, sum + i);}
}int main() {cin >> n;ans[0] = 1;dfs(1, 0);return 0;
}
相关文章:

深度优先搜索(dfs)题目合集
深度优先搜索(dfs)题目合集 全排列问题 dfs原理和模版深度优先搜索原理(纯个人理解)参考程序dfs通用模版 素数环组合的输出 剪枝新dfs模版参考程序新的dfs模版 自然数的拆分 利用形参进行回溯 全排列问题 dfs原理和模版 P1706 全…...
性能监控利器:Ubuntu 22.04 上的 Zabbix 安装与配置指南
简介 今天我们来聊聊如何在 Ubuntu 22.04 上安装和配置 Zabbix。我们会用到 PostgreSQL 作为数据库后端,Nginx 作为 Web 服务器,并用 Let’s Encrypt SSL 证书来保驾护航。 什么是 Zabbix? Zabbix 是一个开源的网络监控和管理解决方案&…...

性能测试的宏观分析:全面提升系统表现的关键
在当今快速发展的软件行业中,系统性能的优劣直接影响用户体验和业务成功。性能测试作为确保系统高效运行的重要环节,其方法和策略不断演进。其中,宏观分析作为一种全面评估系统性能的手段,日益受到关注。本文将深入探讨宏观分析在…...
ctfshow
1,web21 Basic认证采用Base64加密方式,Base64解码字符串发现是 用户名:密码 的格式进行Base64编码。 密码shark63 2,web22 用 子域名扫描器 扫出flag.ctf.show拿到flag,但这个域名已经没了所以就直接交的官方提供的flag。 3,web23 这段PHP代码是一个简单…...

【分享一个vue指令】鼠标放置提示指令v-tooltip
描述 自定义指令 v-tooltip mounted(el, binding):当元素被挂载到DOM上时,这个钩子会被调用。 el 是指令绑定的元素,binding 包含了指令的值,即 binding.value,这里是 clickOutside 字符串。tooltip 变量用于存储创建…...

掌握 Spring 事务管理:深入理解 @Transactional 注解
在业务方法上使用Transactional开启声明式事务时,很有可能由于使用方式有误,导致事务没有生效。 环境准备 表结构 CREATE TABLE admin (id bigint(20) unsigned NOT NULL AUTO_INCREMENT,username varchar(255) DEFAULT NULL,password varchar(255) …...

字符三角形
字符三角形 C语言代码C语言代码Java语言代码Python语言代码 💐The Begin💐点点关注,收藏不迷路💐 给定一个字符,用它构造一个底边长5个字符,高3个字符的等腰字符三角形。 输入 输入只有一行, …...

【LLM】一文学会SPPO
博客昵称:沈小农学编程 作者简介:一名在读硕士,定期更新相关算法面试题,欢迎关注小弟! PS:哈喽!各位CSDN的uu们,我是你的小弟沈小农,希望我的文章能帮助到你。欢迎大家在…...

如何通过ChatGPT提高自己的编程水平
在编程学习的过程中,开发者往往会遇到各种各样的技术难题和学习瓶颈。传统的学习方法依赖书籍、教程、视频等,但随着技术的不断发展,AI助手的崛起为编程学习带来了全新的机遇。ChatGPT,作为一种强大的自然语言处理工具,…...

NVR管理平台EasyNVR多品牌NVR管理工具的流媒体视频融合与汇聚管理方案
随着信息技术的飞速发展,视频监控已经成为现代社会安全管理和业务运营不可或缺的一部分。无论是智慧城市、智能交通、还是大型企业、校园安防,视频监控系统的应用都日益广泛。NVR管理平台EasyNVR,作为功能强大的流媒体服务器软件,…...

python之使用django框架开发web项目
本问将对django框架在python的web项目中的使用进行介绍,有不对之处,烦请指正。 首先使用创建一个django工程(本示例中使用pycharm2024+python3.12),名称和项目保存路径根据自己的需要自行修改,新手直接默认本机环境就好(关于conda将会另开一篇进行讲解。),最后点击cre…...

ChatGPT 桌面版发布了,如何安装?
本章教程教大家如何进行安装。 一、下载安装包 官网地址地址:https://openai.com/chatgpt/desktop/ 支持Windows和MacOS操作系统 二、安装步骤 Windows用户下载之后,会有一个exe安装包,点击运行安装即可。 注意事项,如果Windows操…...

ubuntu 配置 多个 git 客户端 账户
Git配置两个或多个账户 https://blog.csdn.net/mainking2003/article/details/134711865 git 提交 不用输入用户名、密码的方法(GIT免密提交) https://blog.csdn.net/wowocpp/article/details/125797263 git config 用法 https://blog.csdn.net/blueb…...

React Native的界面与交互
React Native (RN) 是一个由 Facebook 开发的开源框架,用于构建跨平台的移动应用程序。它允许开发者使用 JavaScript 和 React 来创建原生 iOS 和 Android 应用。RN 的出现极大地简化了移动应用的开发过程,使得开发者可以更快速、更高效地构建高质量的应…...

autogen+ollama+litellm实现本地部署多代理智能体
autogen 是一个专门为大语言模型 (LLMs) 驱动的自治代理 (autonomous agents) 设计的 Python 库,由 Microsoft 开发和维护。它通过高度模块化和可扩展的架构,支持用户快速构建和运行多代理系统,这些代理可以在没有明确人类干预的情况下协作完成复杂任务。AutoGen 支持以最少…...
InstantStyle容器构建指南
一、介绍 InstantStyle 是一个由小红书的 InstantX 团队开发并推出的图像风格迁移框架,它专注于解决图像生成中的风格化问题,旨在生成与参考图像风格一致的图像。以下是关于 InstantStyle 的详细介绍: 1.技术特点 风格与内容的有效分离 &a…...
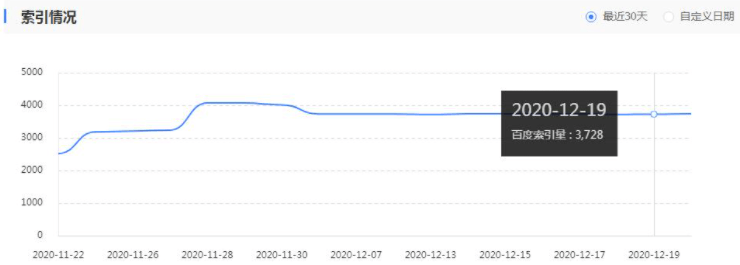
百度主动推送可以提升抓取,它能提升索引量吗?
站长在建站SEO的时候,需要用到百度站长平台(资源平台)的工具,在站长工具中【普通收录】-【资源提交】-【API提交】这个功能,对网站的抓取进行一个提交。 这里估计很多站长就有疑问,如果我主动推送…...

A045-基于spring boot的个人博客系统的设计与实现
🙊作者简介:在校研究生,拥有计算机专业的研究生开发团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹 赠送计算机毕业设计600…...

JavaEE 【知识改变命运】02 多线程(1)
文章目录 线程是什么?1.1概念1.1.1 线程是什么?1.1.2 为什么要有线程1.1.3 进程和线程的区别1.1.4 思考:执行一个任务,是不是创建的线程或者越多是不是越好?(比如吃包子比赛)1.1.5 ) Java 的线程…...
)
Pytorch使用手册-Transforms(专题四)
Transforms(变换) 在 PyTorch 数据处理中的重要性和使用方法,特别是如何通过 torchvision.transforms 模块对数据进行预处理和变换,使其适合用于训练机器学习模型。以下是具体的内容解读: 什么是 Transforms? 数据通常在收集后并非直接适合用于训练机器学习模型,需要通…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
