对撞双指针(七)三数之和
15. 三数之和
给你一个整数数组
nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
首先利用双指针思想进行寻找合适的三个数,再利用set进行去重。
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();set<vector<int>> res;sort(nums.begin(), nums.end());for(int i = n-1; i > 1; i--){int c = nums[i];int temp = 0-c;int left = 0, right = i-1;while(left < right){if(nums[left] + nums[right] < temp)left++;else if(nums[left] + nums[right] > temp)right--;else{res.insert({nums[left], nums[right], c});left++;}}}vector<vector<int>> ret;for(auto it : res){ret.push_back(it);}return ret;}
};离谱……………………

对于去重的方法有进一步优化

将c从右向左固定:
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();vector<vector<int>> ret;sort(nums.begin(), nums.end()); 1、排序for(int i = n-1; i > 1; ){int c = nums[i];int temp = 0-c;int left = 0, right = i-1;while(left < right) 2、此处使用双指针思想{if(nums[left] + nums[right] < temp)left++;else if(nums[left] + nums[right] > temp)right--;else{ret.push_back({nums[left], nums[right], c});int flag = nums[left++];while(left<right && nums[left] == flag) left++; 3、对于去重操作的优化①flag = nums[right--];while(left<right && nums[right] == flag)right--;}}i--; 4、去重的优化②while(i>1 && nums[i+1] == nums[i]) // 把whlie写错成if调试半天才发现i--;}return ret;}
};将c从左向右固定
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();sort(nums.begin(), nums.end()); // 1、排序vector<vector<int>> ret;for(int i = 0; i < n; ){if(nums[i] > 0) break; // 2、作一个小优化,如果左边数大于零则无法满足和为0int left = i+1, right = n-1;int target = -nums[i];while(left < right) // 3、双指针进行寻找{int sum = nums[left] + nums[right];if(sum < target) left++;else if(sum > target) right--;else{ret.push_back({nums[i], nums[left++], nums[right--]});while(left < right && nums[left] == nums[left-1])left++; // 当left位置重复时,left后移while(left < right && nums[right] == nums[right+1])right--; // 当right位置重复时,right左移}}i++;while(i < n && nums[i]==nums[i-1])i++;}return ret;}
};相关文章:

对撞双指针(七)三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组…...
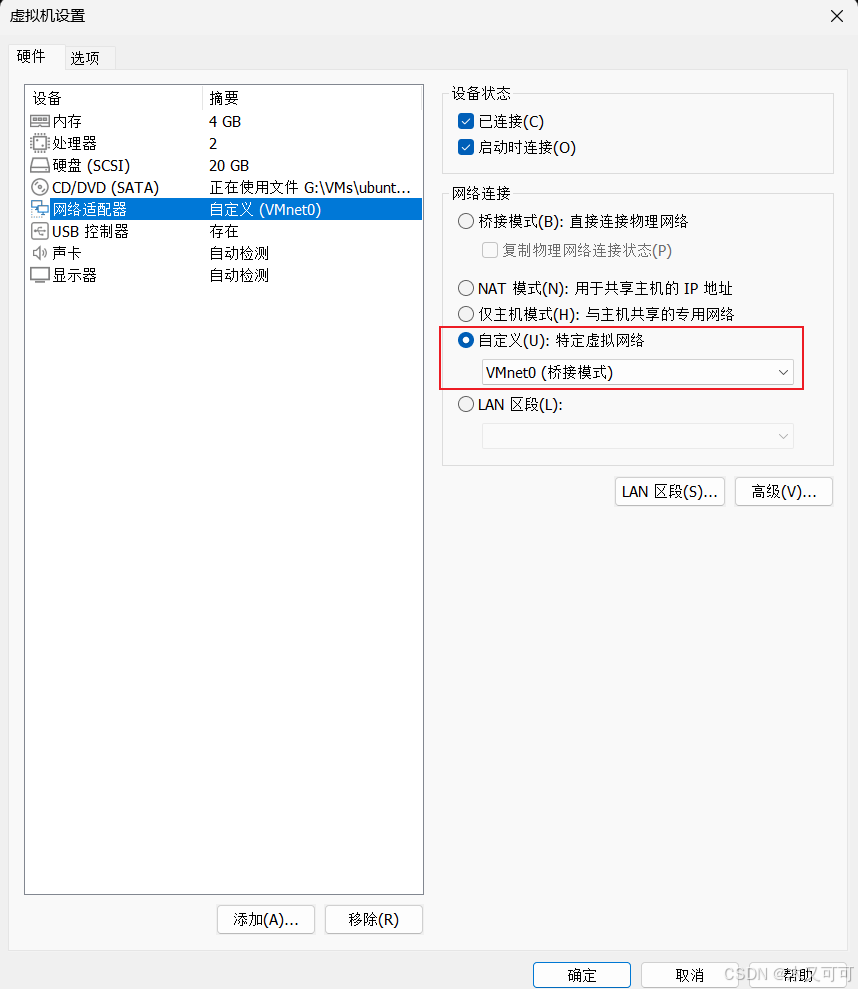
【Ubuntu24.04】服务部署(虚拟机)
目录 0 背景1 安装虚拟机1.1 下载虚拟机软件1.2 安装虚拟机软件1.2 安装虚拟电脑 2 配置虚拟机2.1 配置虚拟机网络及运行初始化脚本2.2 配置服务运行环境2.2.1 安装并配置JDK172.2.2 安装并配置MySQL8.42.2.3 安装并配置Redis 3 部署服务4 总结 0 背景 你的服务部署在了你的计算…...

timm库加载的模型可视化
在深度学习中,模型的可视化有助于了解模型的结构和层级关系。以下是几种方式来可视化使用 timm 库加载的模型: 打印模型结构 torch.nn.Module 的子类(包括 timm 的模型)可以通过 print() 查看其结构:import timm# 加…...

服务限流、降级、熔断-SpringCloud
本文所使用的组件:Nacos(服务中心和注册中心)、OpenFeign(服务调用)、Sentinel(限流、降级)、Hystrix(熔断) 项目结构: service-provider:提供服…...
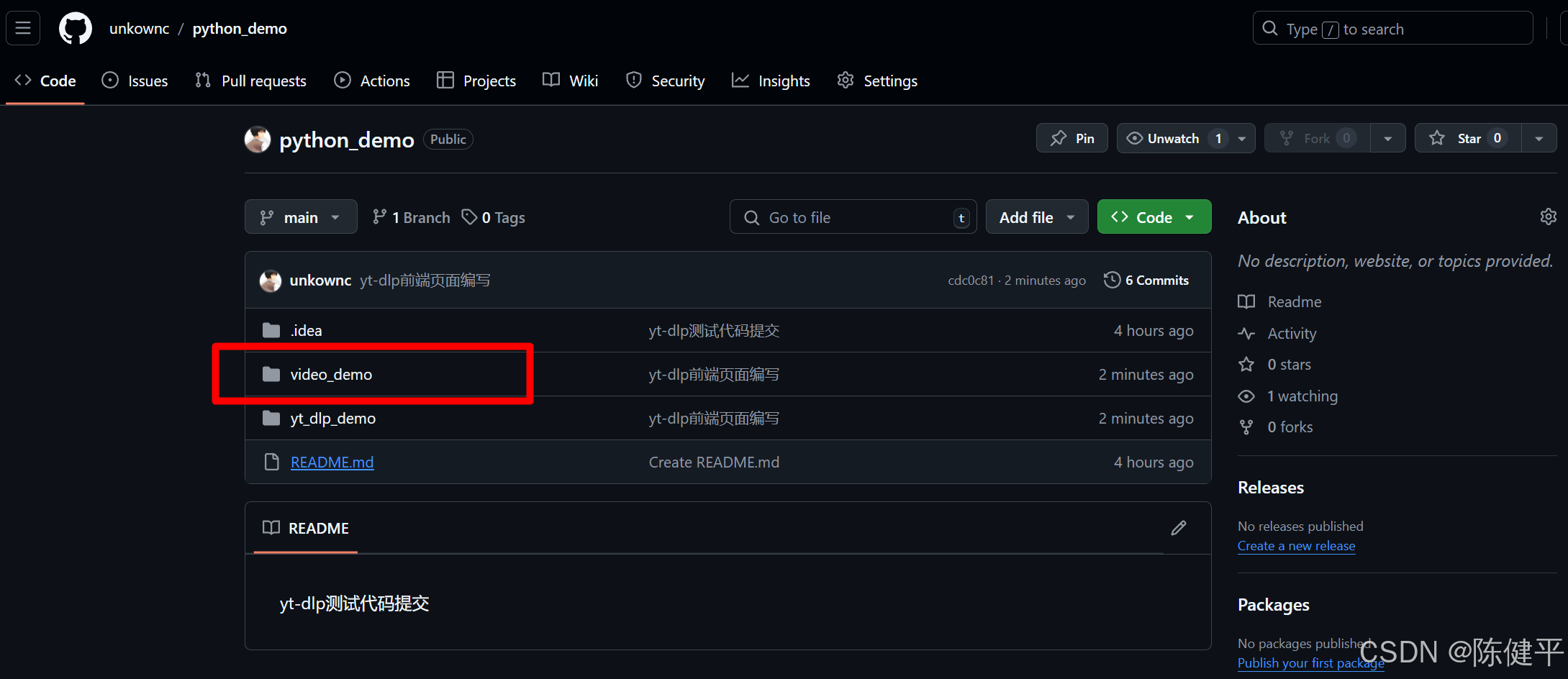
2024最新YT-DLP使用demo网页端渲染
2024最新YT-DLP使用demo网页端渲染 前提摘要1.使用python的fastapi库和jinjia2库进行前端渲染2.代码实现1)目录结构2)代码style.cssindex.htmlresult.htmlmain.pyrun.py 3)运行测试命令端运行 3.项目下载地址 前提摘要 2024最新python使用yt…...

《第十部分》1.STM32之通信接口《精讲》之IIC通信---介绍
经过近一周的USART学习,我深刻体会到通信对单片机的重要性。它就像人类的手脚和大脑,只有掌握了通信技术,单片机才能与外界交互,展现出丰富多彩的功能,变得更加强大和实用。 单片机最基础的“语言”是二进制。可惜&am…...
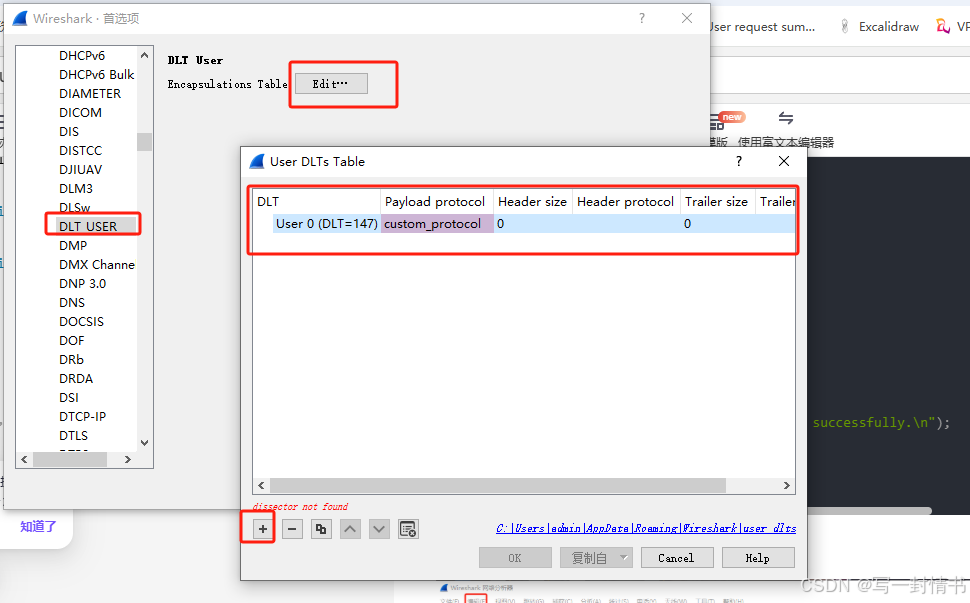
wireshark使用lua解析自定义协议
wireshark解析自定义协议 1.自定义的lua放入路径2.修改init.lua2.1 开启lua2.2 init.lua文件最后加入自己的lua文件位置,这里需要确保与自己的文件名相同 3.编写lua4.编写c抓包5.wireshark添加自定义协议如何加调试信息 1.自定义的lua放入路径 一般是自己软件的安装…...
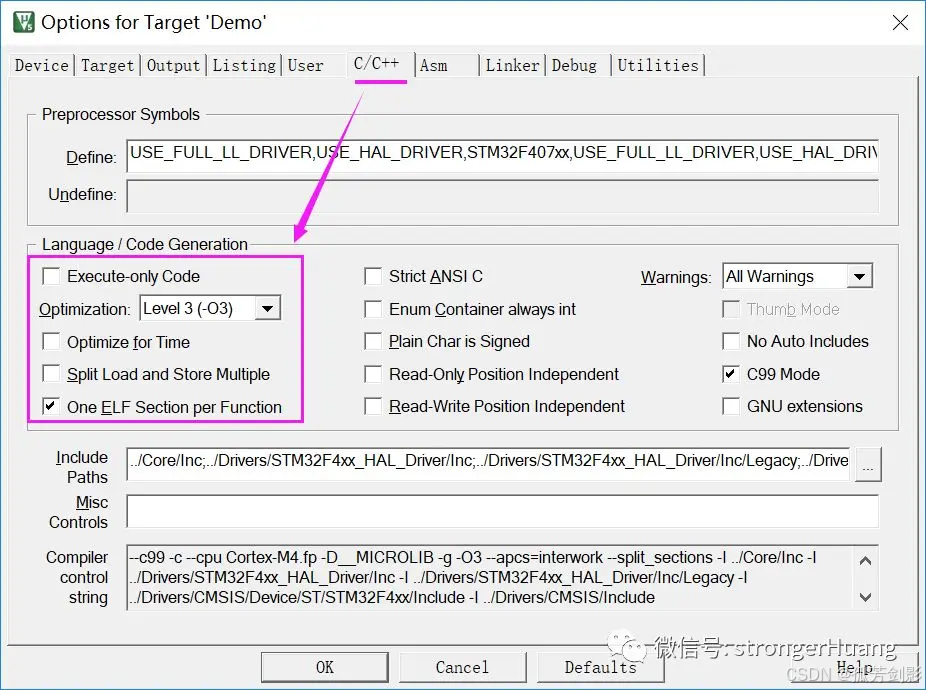
(Keil)MDK-ARM各种优化选项详细说明、实际应用及拓展内容
参考 MDK-ARM各种优化选项详细说明、实际应用及拓展内容 本文围绕MDK-ARM优化选项,以及相关拓展知识(微库、实际应用、调试)进行讲述,希望对你今后开发项目有所帮助。 1 总述 我们所指的优化,主要两方面: 1.代码大小(Size) 2.代码性能(运行时间) 在MDK-ARM中,优…...
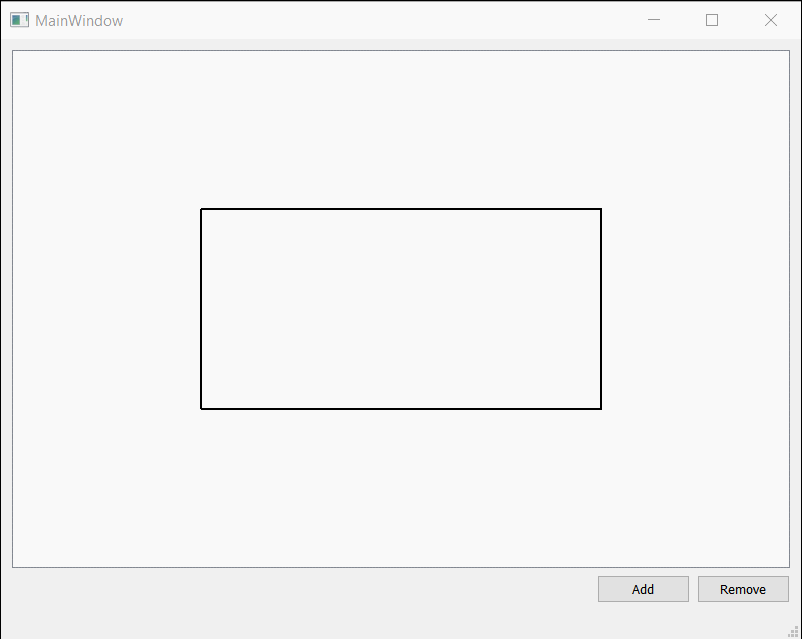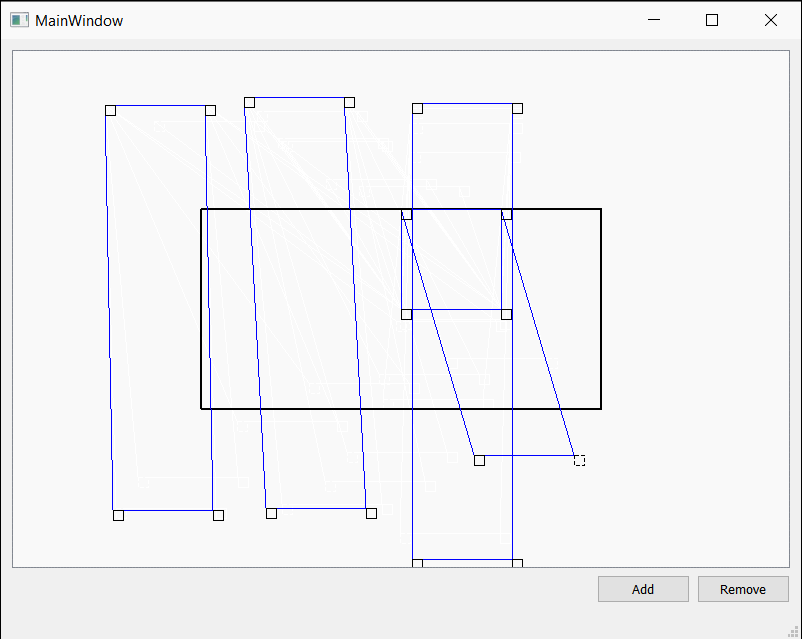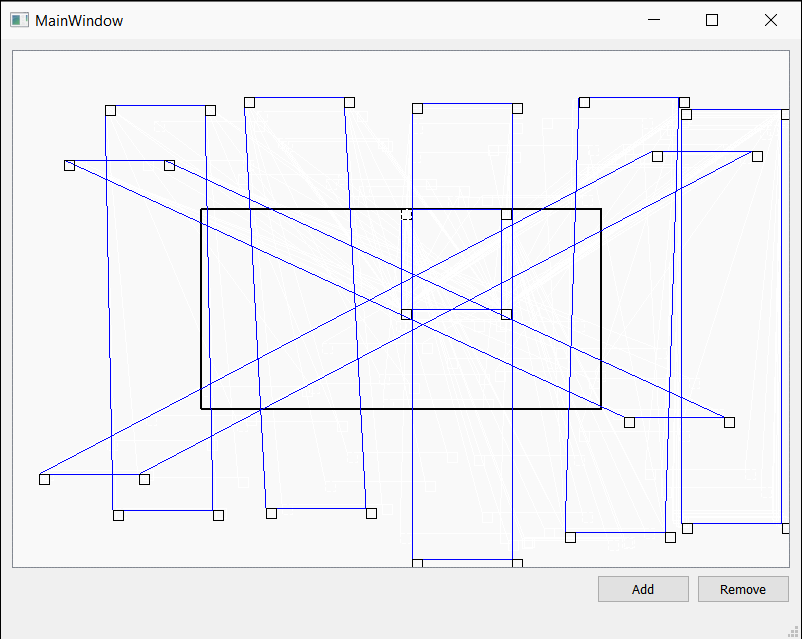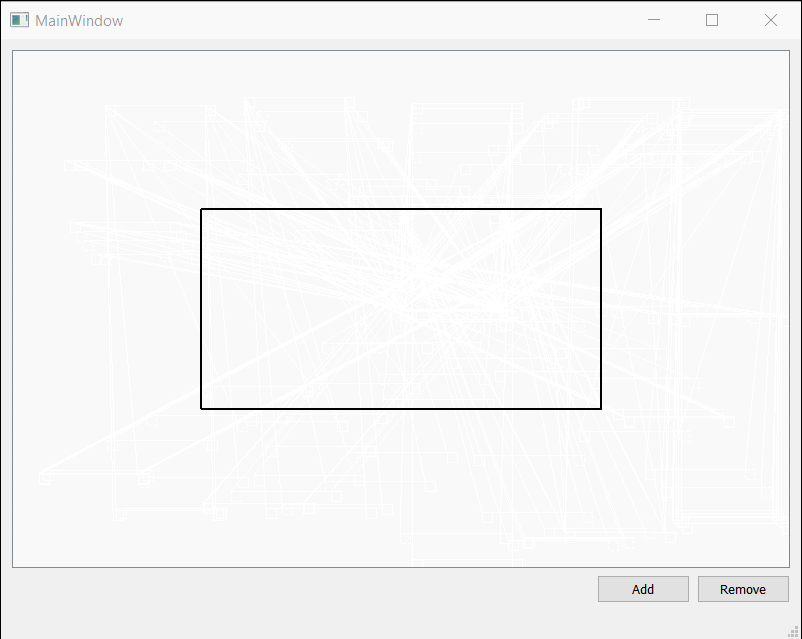
Qt实现可拖拽的矩形
之前项目上需要用Qt来绘制可拖拽改变形状的矩形。看了Qt Graphics相关的内容,虽然对Qt怎么添加图元的有了些了解,但是具体如何实现拖拽效果,一时也没有什么好的想法。还好网上有人分享的例子,很受启发。后来又回顾了一下这部分的代…...
,B服务器下载A服务器文件(下载))
CentOS:A服务器主动给B服务器推送(上传),B服务器下载A服务器文件(下载)
Linux:常识(bash: ip command not found )_bash: ip: command not found-CSDN博客 rsync 中断后先判断程序是否自动重连:ps aux | grep rsync 查看目录/文件是否被使用(查询线程占用):lsof /usr/local/bin/mongodump/.B_database1.6uRCTp 场景:MongoDB中集合非常大需要…...

Oracle 执行计划查看方法汇总及优劣对比
在 Oracle 数据库中,查看执行计划是优化 SQL 语句性能的重要工具。以下是几种常用的查看执行计划的方法及其优劣比较: 1. 使用 EXPLAIN PLAN FOR 和 DBMS_XPLAN.DISPLAY 方法 执行 EXPLAIN PLAN FOR 语句: EXPLAIN PLAN FOR SELECT * FROM …...

TCL大数据面试题及参考答案
Mysql 索引失效的场景 对索引列进行运算或使用函数:当在索引列上进行数学运算、函数操作等,索引可能失效。例如,在存储年龄的列上建立了索引,若查询语句是 “SELECT * FROM table WHERE age + 1 = 20”,这里对索引列 age 进行了加法运算,数据库会放弃使用索引而进行全表扫…...
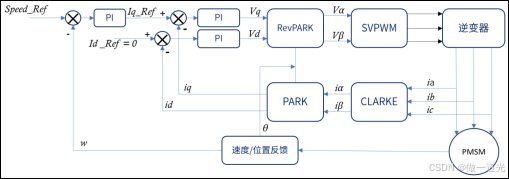
九、FOC原理详解
1、FOC简介 FOC(field-oriented control)为磁场定向控制,又称为矢量控制(vectorcontrol),是目前无刷直流电机(BLDC)和永磁同步电机(PMSM)高效控制的最佳选择…...
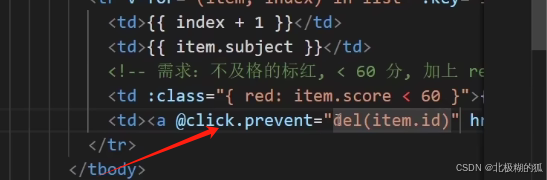
vue页面成绩案例(for渲染表格/删除/添加/统计总分/平均分/不及格显红色/输入内容去首尾空格trim/输入内容转数字number)
1.使用v-if 和v-else 完成<tbody>标签的条件渲染 2.v-for完成列表渲染 3.:class完成分数标红的条件控制 删哪个就传哪个的id,基于这个id去过滤掉相同id的项,把剩下的项返回 a标签的默认点击事件会跳转 这里要禁止默认事件 即使用click.provent 就…...
STM32编程小工具FlyMcu和STLINK Utility 《通俗易懂》破解
FlyMcu FlyMcu 模拟仿真软件是一款用于 STM32 芯片 ISP 串口烧录程序的专用工具,免费,且较为非常容易下手,好用便捷。 注意:STM32 芯片的 ISP 下载,只能使用串口1(USART1),对应的串口…...

Centos使用docker搭建Graylog日志平台
日志管理系统有很多,比如ELK,Graylog,LokiGrafanaPromtail 适用场景: 1.如果需求复杂,服务器资源不受限制,推荐使用ELK(Logstash Elasticsearch Kibana)方案; 2.如果需求仅是将…...

自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例
Kafka:分布式消息系统的核心原理与安装部署-CSDN博客 自定义 Kafka 脚本 kf-use.sh 的解析与功能与应用示例-CSDN博客 Kafka 生产者全面解析:从基础原理到高级实践-CSDN博客 Kafka 生产者优化与数据处理经验-CSDN博客 Kafka 工作流程解析:…...

【SQL】【数据库】语句翻译例题
SQL自然语言到SQL翻译知识点 以下是将自然语言转化为SQL语句的所有相关知识点,分门别类详细列出,并结合技巧说明。 1. 数据库操作 创建数据库 自然语言:创建一个名为“TestDB”的数据库。 CREATE DATABASE TestDB;技巧:识别**“创…...

linux基本命令2
7. 文件查找和搜索 (继续) find — 查找文件 find /path/to/search -name "file_name" # 根据名称查找文件 find /path/to/search -type f # 查找所有普通文件 find /path/to/search -type d # 查找所有目录 find /path/to/search -name "*.txt" # 查找…...

Spring Boot项目集成Redisson 原始依赖与 Spring Boot Starter 的流程
Redisson 是一个高性能的 Java Redis 客户端,提供了丰富的分布式工具集,如分布式锁、Map、Queue 等,帮助开发者简化 Redis 的操作。在集成 Redisson 到项目时,开发者通常有两种选择: 使用 Redisson 原始依赖。使用 Re…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
