二叉树路径相关算法题|带权路径长度WPL|最长路径长度|直径长度|到叶节点路径|深度|到某节点的路径非递归(C)
带权路径长度WPL
二叉树的带权路径长度(WPL)是二叉树所有叶节点的带权路径长度之和,给定一棵二叉树T,采用二叉链表存储,节点结构为

其中叶节点的weight域保存该节点的非负权值,设root为指向T的根节点的指针,设计求WPL的算法
算法思想
![![[Pasted image 20241120144005.png]]](https://i-blog.csdnimg.cn/direct/80410ce82be74fc4bd3ef4a2e5c54c6e.png)
方法1,树中全部叶节点的带权路径长度之和
采用递归思想
二叉树的WPL值 = 树中全部叶节点的带权路径长度之和 = 根节点左子树中全部叶节点的带权路径长度之和 + 根节点右子树中全部叶节点的带权路径长度之和
叶节点的带权路径长度 = 该节点的weight域的值 x 该节点的深度
设根节点的深度为0,若某节点的深度为d,其子节点的深度为d+1
递归过程中,如果遍历到叶节点,返回该节点的带权路径长度,否则返回其左右子树的带权路径长度之和
先遍历5,d是0,不是叶子节点,递归3和7,d为1,3不是叶子节点,7是叶子节点,返回1x7,再递归1和4,d为2,都是叶子节点,返回1x2和4x2,所以WPL为2+8+7=17
typedef struct node
{int weight;struct node *left, *right;
}BTNode;// 传入根节点,调用递归函数,初始深度d为0
int WPL(BTNode* root)
{return WPL1(root, 0);
}// 传入节点和该节点的深度
int WPL1(BTNode* root, int d)
{// 如果该节点是叶子节点,返回该叶子节点的weightxd,也就是带权路径长度if (root->left == NULL && root->right == NULL)return (root->weight * d);// 否则递归该节点的左孩子和右孩子,子节点的深度为根节点的深度+1elsereturn (WPL1(root->left, d + 1) + WPL1(root->right, d + 1));
}
WPL1是一个递归函数,用来计算从当前节点开始的WPL
最长路径长度
给定一个二叉树的root,返回最长的路径的长度,这个路径中的每个节点具有相同值。这条路径可以经过也可以不经过根节点。两个节点之间的路径的长度由它们之间的边数表示
算法思想
符合要求的左子树路径最大长度leftpath,符合要求的右子树路径最大长度rightpath,最后的路径长度为当前路径,与rightpath+leftpath最大值,注意全局变量的初始化位置
![![[Pasted image 20241120204702.png]]](https://i-blog.csdnimg.cn/direct/6101162aeda3439981c9d844eb823c47.png)
第一层
递归计算root的左右孩子的最长单向路径
右节点存在且与当前节点值相等,都是5
rightpath = right+1
![![[Pasted image 20241120205655.png]]](https://i-blog.csdnimg.cn/direct/4f9eaa5118cc403eaee55bd1f05a9944.png)
第二层
right是右节点的DFS返回的值;
递归计算这个节点的左右孩子的最长单向路径,
同样右节点存在且与当前值相等,都是5
rightpath = right+1
![![[Pasted image 20241120205727.png]]](https://i-blog.csdnimg.cn/direct/e4fd2071c1c74cf3a7a8d08d1820641a.png)
第三层
right是右孩子返回的值,
递归左右孩子,为空,返回0
left和right都是0,path也是0,最后返回0
返回第二层
right是0,rightpath是1,path更新为1,返回1
返回第一层
right是1,rightpath是2,path更新为2,返回2
int path; // 全局变量,用于存储当前发现的最长路径长度
// 返回两个正数中的较大值
int Max(int a, int b)
{return a >= b ? a : b;
}
// 递归地计算以root为根的子树中,以相同节点值构成的最长路径
int DFS(BTNode* root)
{// 如果当前节点为空,返回0,因为没有路径if (root == NULL)return 0;int left;int right;int leftpath = 0;int rightpath = 0;// 递归计算左子树和右子树的最长单向路径// left是左子树的最长路径,right是右子树的最长路径left = DFS(root->left);right = DFS(root->right);// 如果左节点存在且与当前节点值相等,最长路径+1if ((root->left) && (root->left->val == root->val))leftpath = left + 1;// 如果右节点存在且与当前节点值相等,最长路径+1if ((root->right) && (root->right->val == root->val))rightpath = right + 1;// leftpath+rightpath,当前节点处的最长路径的长度,经过当前节点// 更新pathpath = Max(path, leftpath + rightpath);// 返回从当前节点向下延伸的最长单项路径,用于供上层节点继续计算return Max(leftpath, rightpath);
}
int longestUnivaluePath(BTNode* root)
{if (root == NULL)return 0;path = 0;DFS(root);return path;
}
直径长度
给定一个二叉树,计算它的直径长度。一棵二叉树的直径长度是任意两个节点路径长度中的最大值。这条路径可能穿过也可能不穿过根节点
算法思想
递归求得节点的左子树的最大深度和右子树的最大深度,相加便是经过该节点的直径,遍历每个节点,更新最大值便可得到该二叉树的最大直径。
- 写出一个求树的最大深度的函数
- 递归调用这个函数,求得每个节点的左子树最大深度和右子树最大深度,相加
![![[Pasted image 20241120211158.png]]](https://i-blog.csdnimg.cn/direct/b2d4b55abb60467e99bc1844b2579886.png)
第一层
将rootA传入depth求深度,传入sum记录直径
递归计算左右子树B和C的深度
第二层
B继续递归左右子树的深度,D和F
C为叶子节点,没有左右孩子,left和right为0,new也就是直径为1,sum更新为1,返回深度为1
第三层
D为叶子节点,new为1,sum还是1,返回深度为1
F为叶子节点,new为1,sum还是1,返回深度为1
返回第二层
B,的left和right都是1,B的new也就是直径是3,sum更新为3,返回深度为2
返回第一层
A,left为2,right为1,new也就是直径为4,sum更新为4,返回深度为3
最后sum=4,返回sum-1 = 3
// 返回两个整数中的较大值
int max(int a, int b)
{return a > b ? a : b;
}// 递归计算二叉树的深度,同时更新全局变量记录直径
int depth(BTNode* root, int* sum)
{// 如果当前节点为空,返回深度为0if (root == NULL)return 0;// 左子树的最大深度int left = depth(root->left, sum);// 右子树的最大深度int right = depth(root->right, sum);// 经过根节点的直径,左子树最大深度与右子树最大深度之和int new = left + right + 1;// 更新sum,记录到目前为止的最大直径*sum = max(*sum, new);// 返回该节点深度的最大值,等于左右子树的最大深度+1return max(left, right) + 1;
}int dimeterBT(BTNode* root)
{if (root == NULL)return 0;int sum = 0;depth(root, &sum);// 返回sum-1,将节点数转换为边数作为直径的定义return sum - 1;
}
到叶节点路径
给你一个二叉树的根节点root,按任意顺序,返回所有从根节点到叶子节点的路径
算法思想
深度优先遍历二叉树,要考虑当前节点以及它的孩子节点,如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点
如果当前节点是叶子节点,则在当前路径末尾添加该节点后就得到了从根节点到叶子节点的路径
![![[Pasted image 20241121142757.png]]](https://i-blog.csdnimg.cn/direct/9e5a14b776004c8ab8408556c5f180d5.png)
将根节点的值1,入到stack深度下标的位置上,深度为0
![![[Pasted image 20241121142855.png]]](https://i-blog.csdnimg.cn/direct/0c19256cc8f84b758628a799ad6aa4c5.png)
有左右孩子,先递归左孩子,深度+1=1
2,入栈
![![[Pasted image 20241121143227.png]]](https://i-blog.csdnimg.cn/direct/0c0f771434fc49e98537689d76aec65f.png)
有右孩子,递归右孩子,5入栈,depth为2
![![[Pasted image 20241121143316.png]]](https://i-blog.csdnimg.cn/direct/978fd63157fd4c59b8e9ef04175f2820.png)
这时候左右孩子节点都为空
将1->2->5的路径保存
- 动态分配一个字符串缓冲区tmp。用于存储当前路径的字符串
1001是缓冲区的长度 - len=0,记录路径字符串的当前长度,即字符串的写入位置,起始为0,表示字符串从头开始写入
- 遍历当前路径中的所有节点值,即stack;使用sprintf追加到路径字符串tmp中
- 添加叶节点值,在路径字符串的末尾,添加当前叶子节点的值
- 将路径字符串存储到结果数组
返回1节点,递归右孩子3,深度为1,入栈,会覆盖掉2,变成3
// 定义二叉树节点结构
typedef struct node
{ int val; struct node* left; struct node* right;
} BTNode; // 辅助函数:递归生成路径
void generatePaths(BTNode* root, char** paths, int* returnSize, int* stack, int depth)
{ if (root == NULL) return; // 将当前节点加入路径栈 stack[depth] = root->val; // 如果是叶子节点,生成路径字符串 if (root->left == NULL && root->right == NULL) { // 分配路径字符串 char* tmp = (char*)malloc(1001); int len = 0; // 构建路径字符串 for (int i = 0; i < depth; i++) { len += sprintf(tmp + len, "%d->", stack[i]); } // 添加叶子节点值 sprintf(tmp + len, "%d", root->val); // 将路径存储到结果数组 paths[(*returnSize)++] = tmp; return; } // 递归遍历左、右子树 generatePaths(root->left, paths, returnSize, stack, depth + 1); generatePaths(root->right, paths, returnSize, stack, depth + 1);
} // 主函数:生成所有路径
char** binaryTreePaths(BTNode* root, int* returnSize)
{ // 分配结果数组 char** paths = (char**)malloc(sizeof(char*) * 1001); *returnSize = 0; // 路径栈 int stack[1001]; // 调用递归函数 generatePaths(root, paths, returnSize, stack, 0); return paths;
}
- binaryTreePaths,输入:root,二叉树的根节点,returnSize,用来返回路径数量
- 返回paths,存储路径字符串的数组
- paths是一个指针数组,用来存储每条路径的字符串
- stack用来记录当前节点的路径值
- generatePaths用来来递归生成路径
generatePaths
- 如果节点root为NULL,直接返回,(递归退出条件)
- 将当前节点的值存入栈
stack[depth]中 - depth表示当前路径的深度
处理叶子节点 - 创建字符串,遍历路径栈stack,通过sprintf拼接路径值,将路径字符串的结果保存在paths中
- 增加路径数量returnSize
遍历左右子树 - 如果当前节点不是叶子节点,遍历递归左子树和右子树
- 子树深度为depth+1
深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点形成树的一条路径,最长路径的长度为树的深度
9
算法思想
如果二叉树为空,深度为0,如果二叉树只有根节点,深度为1
如果二叉树的根节点只有左子树,深度为左子树的深度+1
如果二叉树的根节点只有右子树,深度为右子树的深度+1
如果二叉树的根节点既有既有左子树又有右子树,深度为左右子树深度最大者+1
int maxDepth(BTNode* root)
{if (root == NULL)return 0;// 当前节点的左子树的深度int Lenleft = maxDepth(root->left);// 当前节点的右子树的深度int Lenright = maxDepth(root->right);// 返回左右子树的深度的较大者+1return Lenleft > Lenright ? Lenleft+1 : Lenright+1;
}
到某节点的路径非递归
假设二叉树采用链式存储结构进行存储,root为根节点,p为任意给定节点
求从根节点到p之间路径的非递归算法
算法思想
采用后序非递归遍历二叉树,栈中保留从根节点到当前节点的路径上的所有节点
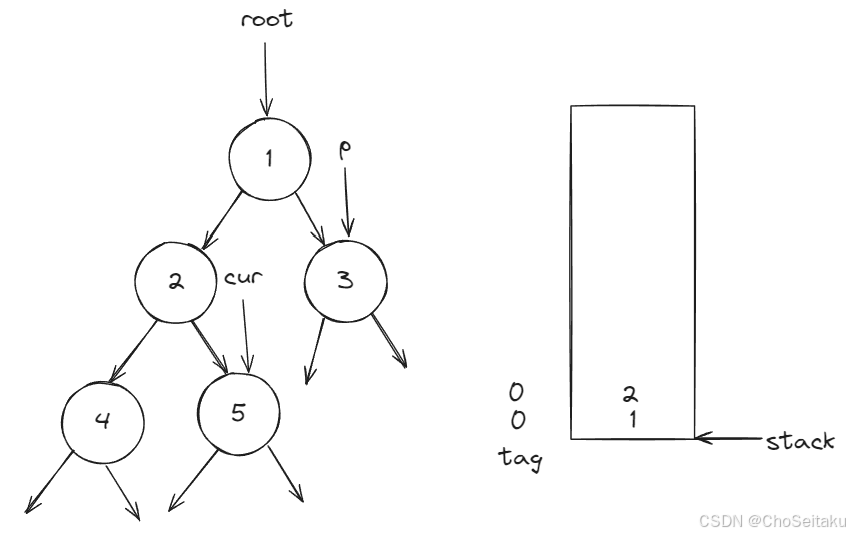
![![[Pasted image 20241121145246.png]]](https://i-blog.csdnimg.cn/direct/8baa34419ff5451ab3a3ef24500e1c54.png)
- cur是当前遍历的节点
- s是栈,用来存储当前节点及其祖先节点,用于后续回溯
- tag数组用于标记每个节点的左右子树是否已经被访问
- top用来表示栈的当前高度
while循环用于实现二叉树的深度优先遍历,只要当前节点不为空或者栈不为空就继续
while循环表示从当前cur节点开始,一直往左遍历,直到没有左子树为止
每次访问一个节点,将该节点入栈,并设置tag为0,表示其右子树未被访问
如果当前节点cur就是p,就打印从根节点到p的路径,通过s栈表示
由于p是3节点,将1,2,4,入栈
![![[Pasted image 20241121150425.png]]](https://i-blog.csdnimg.cn/direct/a38580d5c4034ba5a3e5a9e98fee80a1.png)
处理右子树,检查tap里的数据,如果右子树被访问过,就弹出该节点,跳过所有已经完全访问过的节点
如果该节点的右子树未被访问,就会进入右子树进行遍历,
遍历4节点的右子树,tag置为1,节点为空,直接返回
![![[Pasted image 20241121150742.png]]](https://i-blog.csdnimg.cn/direct/f0799c61e5c74b2baf56a41c7bd95f31.png)
这是循环过来,4被访问过,出栈
![![[Pasted image 20241121150805.png]]](https://i-blog.csdnimg.cn/direct/36e00d17fe6d49d294b87e6dd52c067e.png)
再遍历2的右节点,
![![[Pasted image 20241121150827.png]]](https://i-blog.csdnimg.cn/direct/572aabc311e049828a8b2db44fe2d7a1.png)
// 查找从根节点到指定节点p的路径
void Path(BTNode* root, BTNode* p)
{if (root == NULL || p == NULL)return;BTNode* cur = root;// 存储节点路径的栈int s[MaxSize];// 栈的当前高度int top = 0;// 标记左右子树是否访问过int tag[MaxSize] = {0};while (cur || top > 0){// 向左走直到最左叶子节点while (cur){// 将当前节点入栈s[++top] = cur;// 标记为未访问右子树tag[top] = 0;// 找到目标节点pif (cur == p){printf("从根节点到p节点的路径为\n");for (int i = 1; i <= top; i++){printf("%d", s[i]->data);if (i < top)printf("->");printf("\n");return;}}// 继续遍历左子树cur = cur->left;}// 如果当前节点的左子树遍历完,回溯到父节点while (top > 0 && tag[top] == 1)// 出栈top--;// 访问右子树if (top > 0){// 访问当前节点的右子树cur = s[top];// 进入右子树cur = cur->right;// 标记右子树已访问tag[top] = 1;}}
}
相关文章:
二叉树路径相关算法题|带权路径长度WPL|最长路径长度|直径长度|到叶节点路径|深度|到某节点的路径非递归(C)
带权路径长度WPL 二叉树的带权路径长度(WPL)是二叉树所有叶节点的带权路径长度之和,给定一棵二叉树T,采用二叉链表存储,节点结构为 其中叶节点的weight域保存该节点的非负权值,设root为指向T的根节点的指针,设计求W…...

前端:JavaScript (学习笔记)【2】
目录 一,数组的使用 1,数组的创建 [ ] 2,数组的元素和长度 3,数组的遍历方式 4,数组的常用方法 二,JavaScript中的对象 1,常用对象 (1)String和java中的Stri…...

[面试]-golang基础面试题总结
文章目录 panic 和 recover**注意事项**使用 pprof、trace 和 race 进行性能调试。**Go Module**:Go中new和make的区别 Channel什么是 Channel 的方向性?如何对 Channel 进行方向限制?Channel 的缓冲区大小对于 Channel 和 Goroutine 的通信有…...
【案例】泛微.齐业成助力北京中远大昌汽车实现数电票全流程管理
中远大昌统一发票共享平台上线三个多月以来,实现: 5000份 60000元 发票开具 成本节约 客户简介及需求分析 北京中远大昌汽车服务有限公司(以下简称“中远大昌”)成立于2002年,是中远海运集团所属香远(北…...

微软安全文章合集
说明:文章来自微软很多年前旧帖,有用的部分拿去,没用的就忽略吧,另外提一句,微软会清理文章,很多我收藏的帖子都无法查看了,所以收藏的最好办法是,用word复制粘贴下来保存到云盘&…...
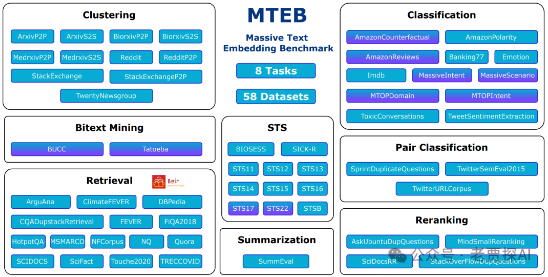
自然语言处理: RAG优化之Embedding模型选型重要依据:mteb/leaderboard榜
本人项目地址大全:Victor94-king/NLP__ManVictor: CSDN of ManVictor git地址:https://github.com/opendatalab/MinerU 写在前面: 笔者更新不易,希望走过路过点个关注和赞,笔芯!!! 写在前面: 笔者更新不易,希望走过路…...

鸿蒙主流路由详解
鸿蒙主流路由详解 Navigation Navigation更适合于一次开发,多端部署,也是官方主流推荐的一种路由控制方式,但是,使用起来入侵耦合度高,所以,一般会使用HMRouter,这也是官方主流推荐的路由 Navigation官网地址 个人源码地址 路由跳转 第一步-定义路由栈 Provide(PageInfo) pag…...

C#构建一个简单的循环神经网络,模拟对话
循环神经网络(Recurrent Neural Network, RNN)是一种用于处理序列数据的神经网络模型。与传统的前馈神经网络不同,RNN具有内部记忆能力,可以捕捉到序列中元素之间的依赖关系。这种特性使得RNN在自然语言处理、语音识别、时间序列预…...

Linux上安装单机版Kibana6.8.1
1. 下载安装包 kibana-6.8.1-linux-x86_64.tar.gz 链接:https://pan.baidu.com/s/1b4kION9wFXIVHuWDn2J-Aw 提取码:rdrc 2. Kibana启动不能使用root用户,使用ES里创建的elsearch用户,进行赋权: chown -R elsearch:els…...
短视频矩阵矩阵,矩阵号策略
随着数字媒体的迅猛发展,短视频平台已经成为企业和个人品牌推广的核心渠道。在这一背景下,短视频矩阵营销策略应运而生,它通过高效整合和管理多个短视频账号,实现资源的最优配置和营销效果的最大化。本文旨在深入探讨短视频矩阵的…...
Rust 力扣 - 2266. 统计打字方案数
文章目录 题目描述题解思路题解代码题目链接 题目描述 题解思路 这题可以先求按了多少次相同连续的按钮,所有的连续相同按钮表示的方案数的乘积就是本题答案 我们的关键问题就转换成了按n个连续相同按钮表示的方案数 设f(i)表示按i个连续相同按钮表示的方案数 如…...
【大数据技术与开发实训】携程景点在线评论分析
景点在线评论分析 题目要求实验目标技术实现数据采集获取所有相关景点页面的 URL获取所有相关景点对应的 poiId 及其他有用信息通过 poiId 获取所有景点的全部评论数据采集结果 数据预处理景点信息的数据预处理查看数据基本信息缺失值处理 用户评论的数据处理缺失值处理分词、去…...

46.坑王驾到第十期:vscode 无法使用 tsc 命令
点赞收藏加关注,你也能住大别墅! 一、问题重现 上一篇帖子记录了我昨天在mac上安装typescript及调试的过程。今天打开vscode准备开干的时候,发现tsc命令又无法使用了,然后按照昨天的方法重新安装调试后又能用了,但是关…...

postman 调用 下载接口(download)使用默认名称(response.txt 或随机名称)
官网地址:https://www.postman.com 介绍 Postman 是一款流行的 API 开发和测试工具,用于发送 HTTP 请求、测试接口、调试服务器响应以及进行 API 文档管理。它支持多种请求类型(如 GET、POST、PUT、DELETE 等),并且功能…...

单片机_简单AI模型训练与部署__从0到0.9
IDE: CLion MCU: STM32F407VET6 一、导向 以求知为导向,从问题到寻求问题解决的方法,以兴趣驱动学习。 虽从0,但不到1,剩下的那一小步将由你迈出。本篇主要目的是体验完整的一次简单AI模型部署流程&#x…...

对撞双指针(七)三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组…...
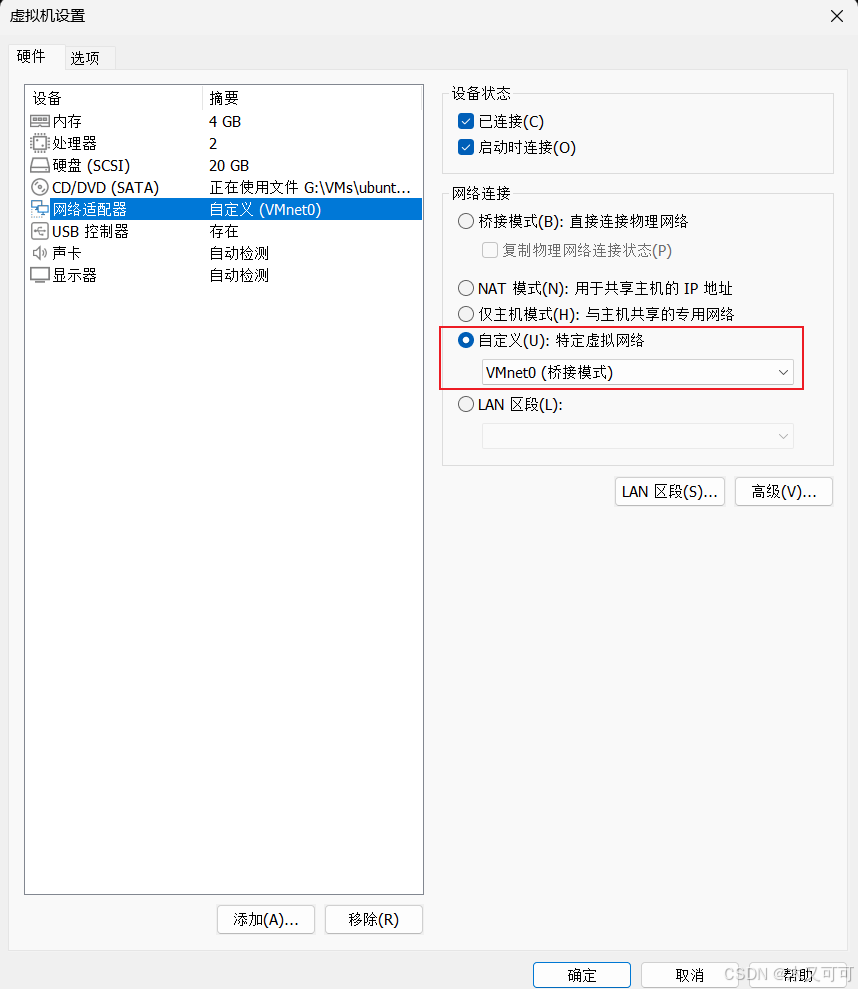
【Ubuntu24.04】服务部署(虚拟机)
目录 0 背景1 安装虚拟机1.1 下载虚拟机软件1.2 安装虚拟机软件1.2 安装虚拟电脑 2 配置虚拟机2.1 配置虚拟机网络及运行初始化脚本2.2 配置服务运行环境2.2.1 安装并配置JDK172.2.2 安装并配置MySQL8.42.2.3 安装并配置Redis 3 部署服务4 总结 0 背景 你的服务部署在了你的计算…...

timm库加载的模型可视化
在深度学习中,模型的可视化有助于了解模型的结构和层级关系。以下是几种方式来可视化使用 timm 库加载的模型: 打印模型结构 torch.nn.Module 的子类(包括 timm 的模型)可以通过 print() 查看其结构:import timm# 加…...

服务限流、降级、熔断-SpringCloud
本文所使用的组件:Nacos(服务中心和注册中心)、OpenFeign(服务调用)、Sentinel(限流、降级)、Hystrix(熔断) 项目结构: service-provider:提供服…...
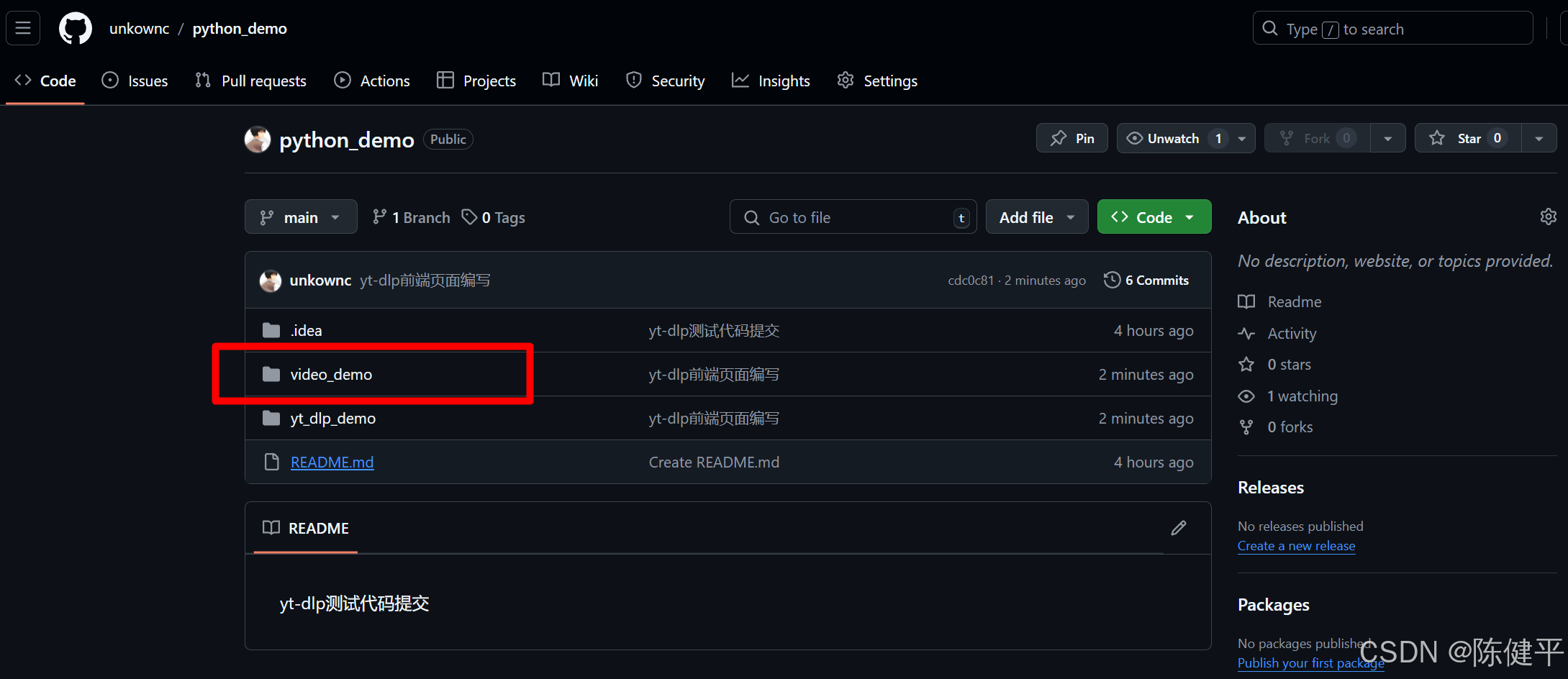
2024最新YT-DLP使用demo网页端渲染
2024最新YT-DLP使用demo网页端渲染 前提摘要1.使用python的fastapi库和jinjia2库进行前端渲染2.代码实现1)目录结构2)代码style.cssindex.htmlresult.htmlmain.pyrun.py 3)运行测试命令端运行 3.项目下载地址 前提摘要 2024最新python使用yt…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...
