算法笔记:并查集
一、什么是并查集
并查集的逻辑结构是一个包含N个元素的集合,如图:

我们将各个元素划分为若干个互不相交的子集,如图:

二、并查集的基本操作
(一)初始化
初始化可以先将每个子集指向自己
//初始化int [] un=new int[10];for (int i = 0; i < un.length; i++) { //先使得每个子集指向子集un[i]=i;}
(二)Find操作
返回指定索引的根
//并查集查询public int find(int x){if (un[x]==x){ //如果当前并查集指向自己 那么直接返回当前值即可return x;}else { //如果不指向自己 则代表有可能有指向链 那么就递归寻找 直到找到最终的根节点return find(un[x]);}}
(三)Union操作
●合并操作即将一个根指向另一个指定节点
//合并 也就是使得i指向jpublic void merge(int i,int j){un[find(i)]=find(j); // un[find(i)] 是指 如果i索引 有指向其他节点的话 那么肯定要遍历到最终指向的父节点 然后将父节点与指定索引值合并 没有指向的话那么就是直接使得当前位置i指向j}(四)Union操作(路径压缩)
//合并(压缩路径)public int union(int x){if (un[x]==x){ //代表此时已经是跟节点return x;}else {un[x]=union(un[x]); //使得每一个节点都指向该父节点 比如1—>2—>3 3是最终根节点 那么这样写的最终效果就是 1->3 2—>3 3->3return un[x]; //返回父节点}}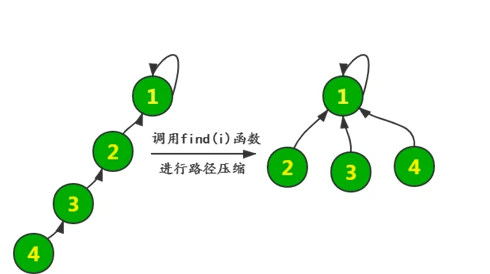

相关文章:

算法笔记:并查集
一、什么是并查集 并查集的逻辑结构是一个包含N个元素的集合,如图: 我们将各个元素划分为若干个互不相交的子集,如图: 二、并查集的基本操作 (一)初始化 初始化可以先将每个子集指向自己 //初始化int []…...

密码系统设计实验3-2
文章目录 《密码系统设计》实验实验项目实验三 密码模块实现4-6 学时实践要求(30 分) 《密码系统设计》实验 实验项目 实验序号实验名称实验学时数实验目的实验内容实验类型学生学习预期成果实验三密码模块实现6基于商用密码标准的密码模块的实现实现简…...
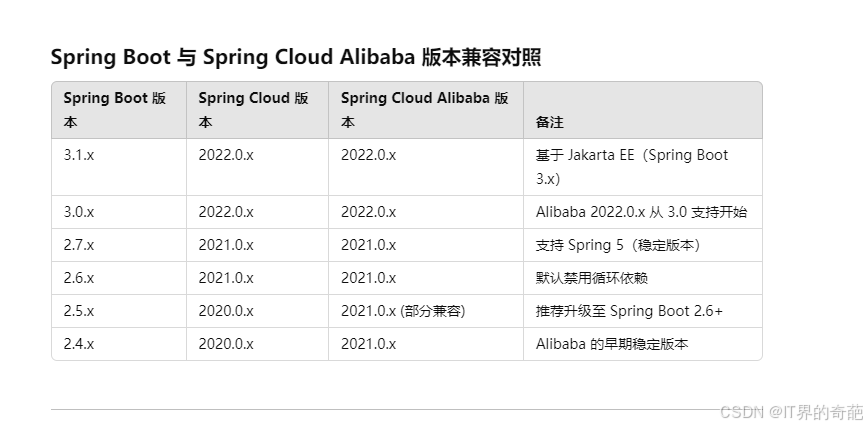
Spring Boot 与 Spring Cloud Alibaba 版本兼容对照
版本选择要点 Spring Boot 3.x 与 Spring Cloud Alibaba 2022.0.x Spring Boot 3.x 基于 Jakarta EE,javax.* 更换为 jakarta.*。 需要使用 Spring Cloud 2022.0.x 和 Spring Cloud Alibaba 2022.0.x。 Alibaba 2022.0.x 对 Spring Boot 3.x 的支持在其发行说明中…...

SVD 奇异值分解
SVD 是一种矩阵分解和降维的算法,通过分解矩阵找到奇异值,奇异值越大代表特征越重要。公式如下 A U Σ V T A U \Sigma V^T AUΣVT U : 左矩阵 ( m \times m ) Σ \Sigma Σ: 对角奇异值矩阵V:右矩阵( n \times n ) Sklearn 实现 S…...

C++设计模式-享元模式
动机(Motivation) 在软件系统采用纯粹对象方案的问题在于大量细粒度的对象会很快充斥在系统中,从而带来很高的运行时代价——主要指内存需求方面的代价。如何在避免大量细粒度对象问题的同时,让外部客户程序仍然能够透明地使用面向对象的方式来进行操作…...

AI加持,华为全屋智能品牌升级为“鸿蒙智家”
1.传统智能家居的困境:从便利到繁琐 近年来,智能家居因其便捷性和科技感受到消费者的青睐。然而,随着用户需求的多样化,传统智能家居的弊端逐渐显现: 设备连接复杂,品牌间兼容性不足,用户不得不…...

洛谷刷题之p1631
序列合并 题目入口 题目描述 有两个长度为 N N N 的单调不降序列 A , B A,B A,B,在 A , B A,B A,B 中各取一个数相加可以得到 N 2 N^2 N2 个和,求这 N 2 N^2 N2 个和中最小的 N N N 个。 输入格式 第一行一个正整数 N N N; 第二…...

uniapp前端开发,基于vue3,element plus组件库,以及axios通讯
简介 UniApp 是一个基于 Vue.js 的跨平台开发框架,旨在通过一次开发、编译后运行在多个平台上,如 iOS、Android、H5、以及小程序(微信小程序、支付宝小程序、百度小程序等)等。UniApp 为开发者提供了统一的开发体验,使…...
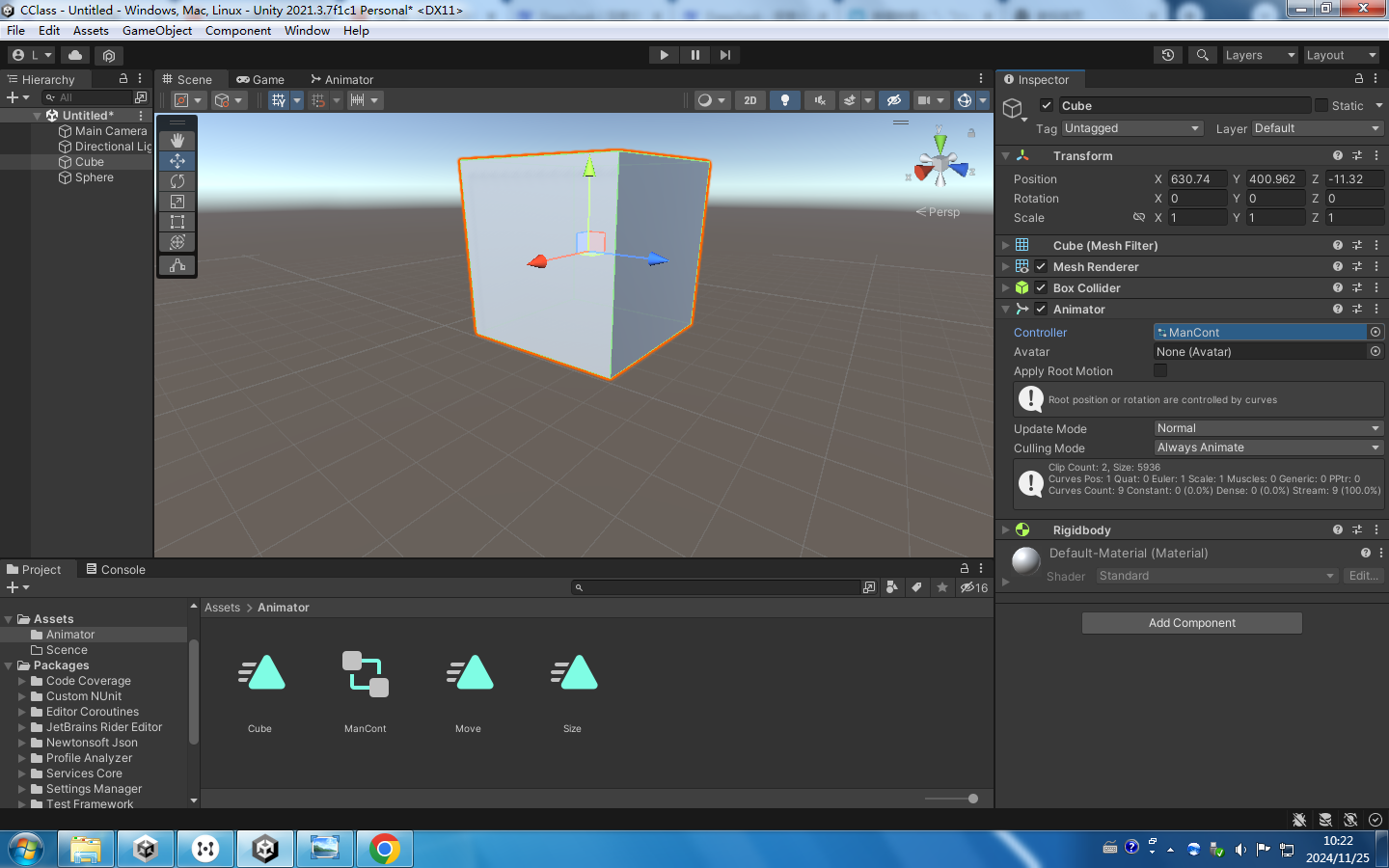
在Unity中实现物体动画的完整流程
在Unity中,动画是游戏开发中不可或缺的一部分。无论是2D还是3D游戏,动画都能为游戏增添生动的视觉效果。本文将详细介绍如何在Unity中为物体添加动画,包括资源的准备、播放组件的添加、动画控制器的创建以及动画片段的制作与调度。 1. 准备动…...

【云计算网络安全】解析 Amazon 安全服务:构建纵深防御设计最佳实践
文章目录 一、前言二、什么是“纵深安全防御”?三、为什么有必要采用纵深安全防御策略?四、以亚马逊云科技为案例了解纵深安全防御策略设计4.1 原始设计缺少安全策略4.2 外界围栏构建安全边界4.3 访问层安全设计4.4 实例层安全设计4.5 数据层安全设计4.6…...

【Andriod ADB基本命令总结】
笔者工作当中遇到安卓机器的数据访问和上传,特来简单总结一下常用命令。 1、ADB命令简介与安装 简介: ADB (Android Debug Bridge) 是一个强大的命令行工具,用于与 Android 设备进行交互,常用于开发、调试、测试以及设备管理等操作。它是 Android 开发工具包(SDK)的一部…...

ChatGPT如何辅助academic writing?
今天想和大家分享一篇来自《Nature》杂志的文章《Three ways ChatGPT helps me in my academic writing》,如果您的日常涉及到学术论文的写作(writing)、编辑(editing)或者审稿( peer review)&a…...

Day 27 贪心算法 part01
贪心算法其实就是没有什么规律可言,所以大家了解贪心算法 就了解它没有规律的本质就够了。 不用花心思去研究其规律, 没有思路就立刻看题解。 基本贪心的题目 有两个极端,要不就是特简单,要不就是死活想不出来。 学完贪心之后再去看动态规划,就会了解贪心和动规的区别。…...

使用Python实现目标追踪算法
引言 目标追踪是计算机视觉领域的一个重要任务,广泛应用于视频监控、自动驾驶、机器人导航、运动分析等多个领域。目标追踪的目标是在连续的视频帧中定位和跟踪感兴趣的物体。本文将详细介绍如何使用Python和OpenCV实现一个基本的目标追踪算法,并通过一…...

某科技研发公司培训开发体系设计项目成功案例纪实
某科技研发公司培训开发体系设计项目成功案例纪实 ——建立分层分类的培训体系,加强培训跟踪考核,促进培训成果实现 【客户行业】科技研发行业 【问题类型】培训开发体系 【客户背景】 某智能科技研发公司是一家专注于智能科技、计算机软件技术开发与…...

如何通过高效的缓存策略无缝加速湖仓查询
引言 本文将探讨如何利用开源项目 StarRocks 的缓存策略来加速湖仓查询,为企业提供更快速、更灵活的数据分析能力。作为 StarRocks 社区的主要贡献者和商业化公司,镜舟科技深度参与 StarRocks 项目开发,也为企业着手构建湖仓架构提供更多参考…...

Linux V4L2框架介绍
linux V4L2框架介绍 V4L2框架介绍 V4L2,全称Video for Linux 2,是Linux操作系统下用于视频数据采集设备的驱动框。它提供了一种标准化的方式使用户空间程序能够与视频设备进行通信和交互。通过V4L2接口,用户可以方便地实现视频图像数据的采…...

【前端】JavaScript 中 arguments、类数组与数组的深入解析
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: 前端 文章目录 💯前言💯什么是 arguments 对象2.1 arguments 的定义2.2 arguments 的特性2.3 使用场景 💯深入了解 arguments 的结构3.1 arguments 的内部结构arguments 的关键属性…...

Android 布局菜单或按钮图标或Menu/Item设置可见和不可见
设置可见和不可见 即 设置 显示和隐藏;是双向设置;什么情况显示,什么情况隐藏分判断的条件 它不同于删除和屏蔽,删除和屏蔽,覆盖是单向的,不可逆转的。它间接等于单向的隐藏!!&…...

|| 与 ??的区别
?? : 空值合并运算符, 用于在左侧操作数为 null 或 undefined 时返回右侧操作数 let name null // null 或者 undefinedlet defaultName defaultNamelet displayName name ?? defaultNameconsole.log(displayName) // defaultName || : 逻辑或,…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
