【机器学习】解构概率,重构世界:贝叶斯定理与智能世界的暗语
文章目录
- 条件概率与贝叶斯定理:深入理解机器学习中的概率关系
- 前言
- 一、条件概率与贝叶斯定理
- 1.1 条件概率的定义与公式
- 1.1.1 条件概率的定义
- 1.1.2 条件概率的实例讲解
- 1.2 条件概率的性质与法则
- 1.2.1 链式法则
- 1.2.2 全概率公式
- 1.2.3 贝叶斯定理的推导
- 1.3 贝叶斯定理详解
- 1.3.1 贝叶斯定理的定义
- 1.3.3 贝叶斯定理的图示说明
- 1.4 朴素贝叶斯分类器
- 1.4.1 朴素贝叶斯的基本原理
- 1.4.2 朴素贝叶斯分类流程
- 1.4.3 朴素贝叶斯的实际应用案例
- 1.4.4 朴素贝叶斯分类器的Python实现
- 1.5 贝叶斯方法在机器学习中的优势与挑战
- 1.5.1 贝叶斯方法的优势
- 1.5.2 贝叶斯方法的挑战
- 二、贝叶斯方法的实际应用
- 2.1 医学检测中的贝叶斯定理
- 2.1.1 先验概率与后验概率
- 2.1.2 检测的准确性
- 2.1.3 应用贝叶斯定理
- 2.1.4 Python代码示例
- 2.2 机器学习中的贝叶斯方法
- 2.2.1 朴素贝叶斯分类器
- 2.2.2 贝叶斯网络
- 2.2.3 贝叶斯优化
- 2.2.4 贝叶斯方法在回归中的应用
- 2.3 贝叶斯方法的扩展与变种
- 2.3.1 多类别朴素贝叶斯
- 2.3.2 高斯朴素贝叶斯
- 三、贝叶斯方法的优势与挑战
- 3.1 贝叶斯方法的优势
- 3.2 贝叶斯方法的挑战
- 四、小结与展望
条件概率与贝叶斯定理:深入理解机器学习中的概率关系
💬 欢迎讨论:在阅读过程中有任何疑问,欢迎在评论区留言,我们一起交流学习!
👍 点赞、收藏与分享:如果你觉得这篇文章对你有帮助,记得点赞、收藏,并分享给更多对机器学习感兴趣的朋友!
🚀 开启概率之旅:条件概率与贝叶斯定理是理解数据关系与模型推断的关键工具。让我们一起探索这些概率概念,揭示机器学习中的隐秘逻辑。
前言
在机器学习的世界中,概率论不仅是数学的一个分支,更是理解数据分布、评估模型性能和进行决策的基石。前两篇博客中,我们分别介绍了线性代数入门和概率论入门,为大家奠定了坚实的数学基础。今天,我们将深入探讨条件概率与贝叶斯定理,这些概念在实际应用中至关重要,特别是在分类、预测和决策模型中。
无论你是刚踏入机器学习领域的小白,还是希望巩固基础的学习者,这篇文章都将帮助你全面理解条件概率与贝叶斯定理的核心概念和实际应用。通过通俗易懂的解释和丰富的实例,我们将一起揭开这些概率工具在机器学习中的奥秘。
一、条件概率与贝叶斯定理
1.1 条件概率的定义与公式
在机器学习中,条件概率帮助我们理解在已知某些信息的情况下,事件发生的概率。
1.1.1 条件概率的定义
条件概率(Conditional Probability)是指在已知某一事件发生的条件下,另一个事件发生的概率。用数学语言表示为:
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P(A|B) = \frac{P(A \cap B)}{P(B)} P(A∣B)=P(B)P(A∩B)
其中:
- P ( A ∣ B ) P(A|B) P(A∣B) 表示在事件 B B B 已经发生的条件下,事件 A A A 发生的概率。
- P ( A ∩ B ) P(A \cap B) P(A∩B) 表示事件 A A A 和事件 B B B 同时发生的概率。
- P ( B ) P(B) P(B) 表示事件 B B B 发生的概率。
1.1.2 条件概率的实例讲解
让我们通过一个简单的例子来理解条件概率。
例子:假设一个袋子中有5个红球和3个蓝球。我们随机抽取一个球,并且抽到蓝球的概率是:
P ( 蓝球 ) = 3 8 P(\text{蓝球}) = \frac{3}{8} P(蓝球)=83
现在,假设我们知道抽到的球是蓝球,求它也是大号球的概率。假设袋子中有2个大号蓝球和1个小号蓝球。那么:
P ( 大号蓝球 ∣ 蓝球 ) = P ( 大号蓝球 ∩ 蓝球 ) P ( 蓝球 ) = 2 8 3 8 = 2 3 P(\text{大号蓝球}|\text{蓝球}) = \frac{P(\text{大号蓝球} \cap \text{蓝球})}{P(\text{蓝球})} = \frac{\frac{2}{8}}{\frac{3}{8}} = \frac{2}{3} P(大号蓝球∣蓝球)=P(蓝球)P(大号蓝球∩蓝球)=8382=32
这意味着在已知抽到蓝球的条件下,抽到大号蓝球的概率是 2 3 \frac{2}{3} 32。
1.2 条件概率的性质与法则
条件概率不仅仅是一个单独的概念,它还具有许多重要的性质和法则,这些都是理解更复杂概率关系的基础。
1.2.1 链式法则
链式法则描述了多个事件联合发生的概率,公式如下:
P ( A ∩ B ) = P ( A ∣ B ) ⋅ P ( B ) = P ( B ∣ A ) ⋅ P ( A ) P(A \cap B) = P(A|B) \cdot P(B) = P(B|A) \cdot P(A) P(A∩B)=P(A∣B)⋅P(B)=P(B∣A)⋅P(A)
这表明联合概率可以通过条件概率与边际概率的乘积来计算。
例子:假设我们有两个事件:
- A A A:下雨
- B B B:带伞
假设:
- P ( A ) = 0.3 P(A) = 0.3 P(A)=0.3(下雨的概率)
- P ( B ∣ A ) = 0.8 P(B|A) = 0.8 P(B∣A)=0.8(下雨时带伞的概率)
- P ( B ∣ ¬ A ) = 0.2 P(B|\neg A) = 0.2 P(B∣¬A)=0.2(不下雨时带伞的概率)
根据链式法则:
P ( A ∩ B ) = P ( B ∣ A ) ⋅ P ( A ) = 0.8 × 0.3 = 0.24 P(A \cap B) = P(B|A) \cdot P(A) = 0.8 \times 0.3 = 0.24 P(A∩B)=P(B∣A)⋅P(A)=0.8×0.3=0.24
1.2.2 全概率公式
全概率公式用于计算一个事件的概率,该事件可以通过多个互斥且完备的子事件来分解。公式如下:
P ( A ) = ∑ i P ( A ∣ B i ) ⋅ P ( B i ) P(A) = \sum_{i} P(A|B_i) \cdot P(B_i) P(A)=i∑P(A∣Bi)⋅P(Bi)
其中, { B i } \{B_i\} {Bi} 是一组互斥且完备的事件集合。
例子:继续以上雨伞的例子,我们可以计算带伞的总概率 P ( B ) P(B) P(B):
P ( B ) = P ( B ∣ A ) ⋅ P ( A ) + P ( B ∣ ¬ A ) ⋅ P ( ¬ A ) = 0.8 × 0.3 + 0.2 × 0.7 = 0.24 + 0.14 = 0.38 P(B) = P(B|A) \cdot P(A) + P(B|\neg A) \cdot P(\neg A) = 0.8 \times 0.3 + 0.2 \times 0.7 = 0.24 + 0.14 = 0.38 P(B)=P(B∣A)⋅P(A)+P(B∣¬A)⋅P(¬A)=0.8×0.3+0.2×0.7=0.24+0.14=0.38
1.2.3 贝叶斯定理的推导
贝叶斯定理是条件概率的一个重要工具,用于反转条件概率。其公式如下:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
推导过程:
从条件概率的定义出发,
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) 和 P ( B ∣ A ) = P ( A ∩ B ) P ( A ) P(A|B) = \frac{P(A \cap B)}{P(B)} \quad \text{和} \quad P(B|A) = \frac{P(A \cap B)}{P(A)} P(A∣B)=P(B)P(A∩B)和P(B∣A)=P(A)P(A∩B)
将 P ( A ∩ B ) P(A \cap B) P(A∩B)从第二个等式代入第一个等式,得到:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
1.3 贝叶斯定理详解
1.3.1 贝叶斯定理的定义
贝叶斯定理(Bayes’ Theorem)是用来计算在已知某些条件下,一个事件发生的概率。它将先验概率、似然函数和边际概率联系起来。
公式为:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
其中:
- P ( A ∣ B ) P(A|B) P(A∣B):后验概率,在事件 B B B 发生后,事件 A A A 发生的概率。
- P ( B ∣ A ) P(B|A) P(B∣A):似然函数,在事件 A A A 发生的条件下,事件 B B B 发生的概率。
- P ( A ) P(A) P(A):先验概率,事件 A A A 发生的初始概率。
- P ( B ) P(B) P(B):边际概率,事件 B B B 发生的总概率。
1.3.3 贝叶斯定理的图示说明
图中展示了先验概率、似然概率和边际概率如何共同影响后验概率的计算。
1.4 朴素贝叶斯分类器
朴素贝叶斯分类器是一种基于贝叶斯定理的简单而强大的分类算法。它在许多实际应用中表现出色,尤其是在文本分类和垃圾邮件过滤等领域。
1.4.1 朴素贝叶斯的基本原理
朴素贝叶斯分类器基于以下假设:
- 条件独立性假设:在给定类别的条件下,特征之间相互独立。
尽管这一假设在现实中往往不成立,但朴素贝叶斯分类器在许多任务中仍然表现出色,尤其是在高维数据和文本分类中。
1.4.2 朴素贝叶斯分类流程
朴素贝叶斯分类器的分类流程如下:
-
训练阶段:
- 计算每个类别的先验概率 P ( C ) P(C) P(C)。
- 计算在每个类别下,每个特征的条件概率 P ( X i ∣ C ) P(X_i|C) P(Xi∣C)。
-
预测阶段:
- 对于一个新的样本,计算其在每个类别下的后验概率 P ( C ∣ X ) P(C|X) P(C∣X)。
- 选择后验概率最大的类别作为预测结果。
1.4.3 朴素贝叶斯的实际应用案例
垃圾邮件过滤是朴素贝叶斯分类器的经典应用之一。通过分析邮件中的词频,朴素贝叶斯能够有效地区分垃圾邮件和正常邮件。
1.4.4 朴素贝叶斯分类器的Python实现
以下是一个简单的朴素贝叶斯分类器的Python实现,用于判断邮件是否为垃圾邮件。
import numpy as np# 简单的二分类示例
# 特征:是否包含特定词汇(1表示包含,0表示不包含)
# 类别:垃圾邮件(Spam)、非垃圾邮件(Not Spam)# 训练数据
X = np.array([[1, 1], # 邮件1: 包含词汇1和词汇2[1, 0], # 邮件2: 包含词汇1,不包含词汇2[0, 1], # 邮件3: 不包含词汇1,包含词汇2[0, 0] # 邮件4: 不包含词汇1和词汇2
])
y = np.array(['Spam', 'Not Spam', 'Spam', 'Not Spam'])# 计算先验概率
P_Y = {}
classes = np.unique(y)
for c in classes:P_Y[c] = np.sum(y == c) / len(y)# 计算条件概率,使用拉普拉斯平滑
P_X_given_Y = {}
for c in classes:X_c = X[y == c]# (出现次数 + 1) / (总样本数 + 2)P_X_given_Y[c] = (np.sum(X_c, axis=0) + 1) / (len(X_c) + 2)# 预测函数
def predict(x):posteriors = {}for c in classes:posteriors[c] = P_Y[c]for i in range(len(x)):if x[i] == 1:posteriors[c] *= P_X_given_Y[c][i]else:posteriors[c] *= (1 - P_X_given_Y[c][i])return max(posteriors, key=posteriors.get)# 测试预测
test_x = [1, 1] # 测试邮件包含词汇1和词汇2
print(f"预测结果: {predict(test_x)}") # 输出: Spam
代码讲解:
- 训练数据:我们有四封邮件,每封邮件有两个特征,表示是否包含特定词汇。类别标签为
Spam或Not Spam。 - 先验概率:计算每个类别在训练数据中的比例。
- 条件概率:在每个类别下,计算每个特征的条件概率。为了避免零概率问题,我们使用了拉普拉斯平滑。
- 预测函数:对于新邮件,根据先验概率和条件概率计算后验概率,选择后验概率最大的类别作为预测结果。
- 测试预测:对一封包含词汇1和词汇2的新邮件进行预测,结果为
Spam。
1.5 贝叶斯方法在机器学习中的优势与挑战
1.5.1 贝叶斯方法的优势
- 简单高效:朴素贝叶斯分类器计算简单,适用于高维数据,尤其在文本分类中表现优异。
- 处理不确定性:能够结合先验知识,处理不确定性和缺失数据。
- 快速训练与预测:由于模型简单,训练和预测速度非常快,适合实时应用。
1.5.2 贝叶斯方法的挑战
- 条件独立性假设:朴素贝叶斯假设特征之间相互独立,这在实际中往往不成立,可能影响模型性能。
- 对连续特征的处理:朴素贝叶斯通常处理离散特征,对于连续特征需要适当的假设和处理方法,如高斯朴素贝叶斯。
- 先验概率的获取:有时先验概率难以准确获取,尤其是在数据不平衡的情况下。
尽管存在这些挑战,朴素贝叶斯仍然是一种强大的分类工具,特别是在特征较多且独立性较强的应用场景中表现出色。
二、贝叶斯方法的实际应用
2.1 医学检测中的贝叶斯定理
贝叶斯定理在医学检测中有广泛的应用,尤其是在诊断测试的准确性评估中。
2.1.1 先验概率与后验概率
先验概率是指在没有任何检测结果之前,一个人患有某种疾病的概率。例如,某疾病的发病率为1%,即:
P ( Disease ) = 0.01 P(\text{Disease}) = 0.01 P(Disease)=0.01
后验概率是指在获得检测结果之后,一个人患有该疾病的概率。例如,检测结果为阳性时,患病的概率。
2.1.2 检测的准确性
假设一种检测有以下特性:
- 真阳性率(Sensitivity): P ( Pos ∣ Disease ) = 0.99 P(\text{Pos}|\text{Disease}) = 0.99 P(Pos∣Disease)=0.99
- 假阳性率(False Positive Rate): P ( Pos ∣ No Disease ) = 0.05 P(\text{Pos}|\text{No Disease}) = 0.05 P(Pos∣No Disease)=0.05
2.1.3 应用贝叶斯定理
我们想计算,在检测结果为阳性的情况下,实际上患有该疾病的概率 P ( Disease ∣ Pos ) P(\text{Disease}|\text{Pos}) P(Disease∣Pos)。
首先,计算边际概率 P ( Pos ) P(\text{Pos}) P(Pos):
P ( Pos ) = P ( Pos ∣ Disease ) ⋅ P ( Disease ) + P ( Pos ∣ No Disease ) ⋅ P ( No Disease ) = 0.99 × 0.01 + 0.05 × 0.99 = 0.0594 P(\text{Pos}) = P(\text{Pos}|\text{Disease}) \cdot P(\text{Disease}) + P(\text{Pos}|\text{No Disease}) \cdot P(\text{No Disease}) = 0.99 \times 0.01 + 0.05 \times 0.99 = 0.0594 P(Pos)=P(Pos∣Disease)⋅P(Disease)+P(Pos∣No Disease)⋅P(No Disease)=0.99×0.01+0.05×0.99=0.0594
然后,应用贝叶斯定理:
P ( Disease ∣ Pos ) = P ( Pos ∣ Disease ) ⋅ P ( Disease ) P ( Pos ) = 0.99 × 0.01 0.0594 ≈ 0.1667 P(\text{Disease}|\text{Pos}) = \frac{P(\text{Pos}|\text{Disease}) \cdot P(\text{Disease})}{P(\text{Pos})} = \frac{0.99 \times 0.01}{0.0594} \approx 0.1667 P(Disease∣Pos)=P(Pos)P(Pos∣Disease)⋅P(Disease)=0.05940.99×0.01≈0.1667
因此,检测结果为阳性时,该人实际上患有该疾病的概率约为16.67%。
2.1.4 Python代码示例
以下是使用Python计算上述概率的示例代码:
# 定义概率
P_Disease = 0.01
P_NoDisease = 1 - P_Disease
P_Pos_given_Disease = 0.99
P_Pos_given_NoDisease = 0.05# 计算边际概率 P(Pos)
P_Pos = P_Pos_given_Disease * P_Disease + P_Pos_given_NoDisease * P_NoDisease# 应用贝叶斯定理计算 P(Disease|Pos)
P_Disease_given_Pos = (P_Pos_given_Disease * P_Disease) / P_Posprint(f"P(Disease|Pos) = {P_Disease_given_Pos:.4f}") # 输出: P(Disease|Pos) = 0.1667
输出:
P(Disease|Pos) = 0.1667
2.2 机器学习中的贝叶斯方法
贝叶斯方法在机器学习中不仅限于分类任务,还广泛应用于回归、聚类和模型选择等领域。
2.2.1 朴素贝叶斯分类器
朴素贝叶斯分类器基于贝叶斯定理和条件独立性假设,适用于文本分类、垃圾邮件过滤、情感分析等任务。
优势:
- 简单高效,适用于高维数据。
- 在文本分类中表现优异,尤其是词汇独立性假设成立时。
劣势:
- 条件独立性假设在实际中往往不成立,可能影响模型性能。
- 对于连续特征需要适当的处理方法。
应用示例:
垃圾邮件过滤、情感分析、文档分类等。
2.2.2 贝叶斯网络
贝叶斯网络是一种图形模型,用于表示变量之间的条件依赖关系。它在因果推断、决策支持系统和复杂系统建模中有广泛应用。
特点:
- 节点表示变量,边表示条件依赖关系。
- 可以处理不完全数据和缺失值。
- 支持因果推断和概率推断。
应用示例:
医学诊断、故障检测、决策支持系统等。
2.2.3 贝叶斯优化
贝叶斯优化是一种基于贝叶斯统计的优化方法,特别适用于高成本或噪声的目标函数优化,如超参数调优。
特点:
- 通过建立目标函数的概率模型(通常为高斯过程)来选择下一个评估点。
- 能有效减少目标函数的评估次数,节省计算资源。
应用示例:
机器学习模型的超参数调优、神经网络架构搜索等。
2.2.4 贝叶斯方法在回归中的应用
贝叶斯方法也可用于回归任务,通过贝叶斯线性回归等方法,提供预测的不确定性估计。
特点:
- 提供参数的后验分布,能够反映模型的不确定性。
- 可以结合先验知识,提升模型的泛化能力。
应用示例:
预测分析、时间序列预测、金融数据建模等。
2.3 贝叶斯方法的扩展与变种
随着机器学习的发展,贝叶斯方法也不断被扩展和改进,以适应更复杂的应用场景。
2.3.1 多类别朴素贝叶斯
多类别朴素贝叶斯扩展了二分类的朴素贝叶斯分类器,能够处理多个类别的分类任务。
特点:
- 适用于多分类问题,如文本分类中的主题分类。
- 保持了条件独立性假设,计算简单高效。
Python代码示例:
import numpy as np# 多类别朴素贝叶斯示例
# 特征:是否包含特定词汇(1表示包含,0表示不包含)
# 类别:不同主题,如Sports, Technology, Politics# 训练数据
X = np.array([[1, 0, 1], # 主题1: Sports[0, 1, 0], # 主题2: Technology[1, 1, 1], # 主题1: Sports[0, 0, 0], # 主题3: Politics[1, 1, 0] # 主题2: Technology
])
y = np.array(['Sports', 'Technology', 'Sports', 'Politics', 'Technology'])# 计算先验概率
P_Y = {}
classes = np.unique(y)
for c in classes:P_Y[c] = np.sum(y == c) / len(y)# 计算条件概率,使用拉普拉斯平滑
P_X_given_Y = {}
for c in classes:X_c = X[y == c]P_X_given_Y[c] = (np.sum(X_c, axis=0) + 1) / (len(X_c) + 2) # 平滑参数=1, 特征数=3# 预测函数
def predict_multiclass(x):posteriors = {}for c in classes:posteriors[c] = P_Y[c]for i in range(len(x)):if x[i] == 1:posteriors[c] *= P_X_given_Y[c][i]else:posteriors[c] *= (1 - P_X_given_Y[c][i])return max(posteriors, key=posteriors.get)# 测试预测
test_x = [1, 0, 1] # 测试样本
print(f"预测结果: {predict_multiclass(test_x)}") # 输出: Sports
输出:
预测结果: Sports
2.3.2 高斯朴素贝叶斯
高斯朴素贝叶斯适用于连续特征,通过假设特征服从高斯分布,计算条件概率。
特点:
- 适用于连续特征,如身高、体重、温度等。
- 利用高斯分布的概率密度函数计算条件概率。
Python代码示例:
import numpy as np
from scipy.stats import norm# 高斯朴素贝叶斯示例
# 特征:身高(cm),体重(kg)
# 类别:男(Male)、女(Female)# 训练数据
X = np.array([[180, 80], # Male[170, 70], # Female[175, 75], # Male[160, 60], # Female[165, 65], # Female[185, 85] # Male
])
y = np.array(['Male', 'Female', 'Male', 'Female', 'Female', 'Male'])# 计算先验概率
P_Y = {}
classes = np.unique(y)
for c in classes:P_Y[c] = np.sum(y == c) / len(y)# 计算每个类别下特征的均值和标准差
parameters = {}
for c in classes:X_c = X[y == c]parameters[c] = {'mean': np.mean(X_c, axis=0),'std': np.std(X_c, axis=0)}# 预测函数
def predict_gaussian(x):posteriors = {}for c in classes:prior = P_Y[c]likelihood = 1for i in range(len(x)):# 使用高斯分布的概率密度函数计算mean = parameters[c]['mean'][i]std = parameters[c]['std'][i]likelihood *= norm.pdf(x[i], mean, std)posteriors[c] = prior * likelihoodreturn max(posteriors, key=posteriors.get)# 测试预测
test_x = [172, 68] # 测试样本
print(f"预测结果: {predict_gaussian(test_x)}") # 输出: Female
输出:
预测结果: Female
三、贝叶斯方法的优势与挑战
3.1 贝叶斯方法的优势
- 处理不确定性:贝叶斯方法能够自然地处理不确定性,通过后验分布提供预测的置信区间。
- 融合先验知识:可以将先验知识融入模型,提升模型的泛化能力,特别是在数据不足时表现出色。
- 灵活性强:贝叶斯方法适用于各种复杂的模型和数据结构,能够扩展到多种应用场景。
- 模型解释性好:通过后验分布,可以更直观地理解模型参数的分布和关系。
3.2 贝叶斯方法的挑战
- 计算复杂度高:尤其是在高维数据和复杂模型中,计算后验分布可能需要大量的计算资源和时间。
- 先验选择敏感:选择不合适的先验分布可能影响模型性能和结果的准确性。
- 模型假设限制:贝叶斯方法依赖于模型假设,如条件独立性和分布假设,若假设不成立,可能导致偏差。
- 实现复杂:相较于一些简单的机器学习算法,贝叶斯方法的实现和调试更为复杂,尤其是对于非专业人士。
尽管存在这些挑战,随着计算能力的提升和优化算法的发展,贝叶斯方法在机器学习中的应用越来越广泛,并在许多领域取得了显著的成果。
四、小结与展望
今天,我们深入探讨了条件概率和贝叶斯定理,并介绍了朴素贝叶斯分类器在实际应用中的重要性。通过通俗易懂的解释和丰富的实例,我们不仅理解了这些概率工具的基本概念,还掌握了它们在机器学习中的实际应用。
小结:
- 条件概率帮助我们理解在已知某些信息的情况下,事件发生的概率。
- 贝叶斯定理提供了一种根据新证据更新概率的方法,是许多机器学习算法的基础。
- 朴素贝叶斯分类器通过简化的假设,依然在许多实际应用中表现出色。
展望:
在下一篇博客中,我们将进一步介绍统计学基础,包括描述性统计、推断统计等内容,为机器学习中的数据分析和模型评估提供更全面的工具和方法。希望通过不断学习,大家能够建立起坚实的概率和统计学基础,进一步提升在机器学习领域的能力和理解。
以上就是关于【机器学习】解构概率,重构世界:贝叶斯定理与智能世界的暗语的内容啦,各位大佬有什么问题欢迎在评论区指正,或者私信我也是可以的啦,您的支持是我创作的最大动力!❤️

相关文章:

【机器学习】解构概率,重构世界:贝叶斯定理与智能世界的暗语
文章目录 条件概率与贝叶斯定理:深入理解机器学习中的概率关系前言一、条件概率与贝叶斯定理1.1 条件概率的定义与公式1.1.1 条件概率的定义1.1.2 条件概率的实例讲解 1.2 条件概率的性质与法则1.2.1 链式法则1.2.2 全概率公式1.2.3 贝叶斯定理的推导 1.3 贝叶斯定理…...

threejs——无人机概念切割效果
主要技术采用着色器的切割渲染,和之前写的风车可视化的文章不同,这次的切割效果是在着色器的基础上实现的,并新增了很多可调节的变量,兄弟们,走曲儿~ 线上演示地址,点击体验 源码下载地址,点击下载 正文 从图中大概可以看出以下信息,一个由线组成的无人机模型,一个由…...

electron学习笔记(一)
1.创建项目 mkdir myelectron npm init npm install --save-dev electron //安装通过以上命令, 我们就有了一个 electron 的项目 之后, 设置主文件入口 , 添加热启动 nodemon 2. nodemon 的使用和配置 要根目录下添加 nodemon.json 文件,配…...

基于Arduino蹲便器的自动清洁系统(论文+源码)
1系统整体设计 经过上述的方案分析,最终确定了Arduino UNO开发板为核心,结合蓝牙模块,舵机,电磁阀,红外传感器,步进电机,舵机等硬件设备来构成整个控制系统,整体框图如图2.1所示。其…...

【JavaWeb后端学习笔记】使用HttpClient发送Http请求
使用HttpClient发送Http请求需要在项目中导入相关依赖: <dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.5.13</version> </dependency>1、 HttpClient…...

2024告别培训班 数通、安全、云计算、云服务、存储、软考等1000G资源分享
大类有:软考初级 软考中级 软考高级 华为认证 华三认证: 软考初级: 信息处理技术员 程序员 网络管理员 软考中级: 信息安全工程师 信息系统监理师 信息系统管理工程师 嵌入式系统设计时 数据库系统工程师 电子商务设…...
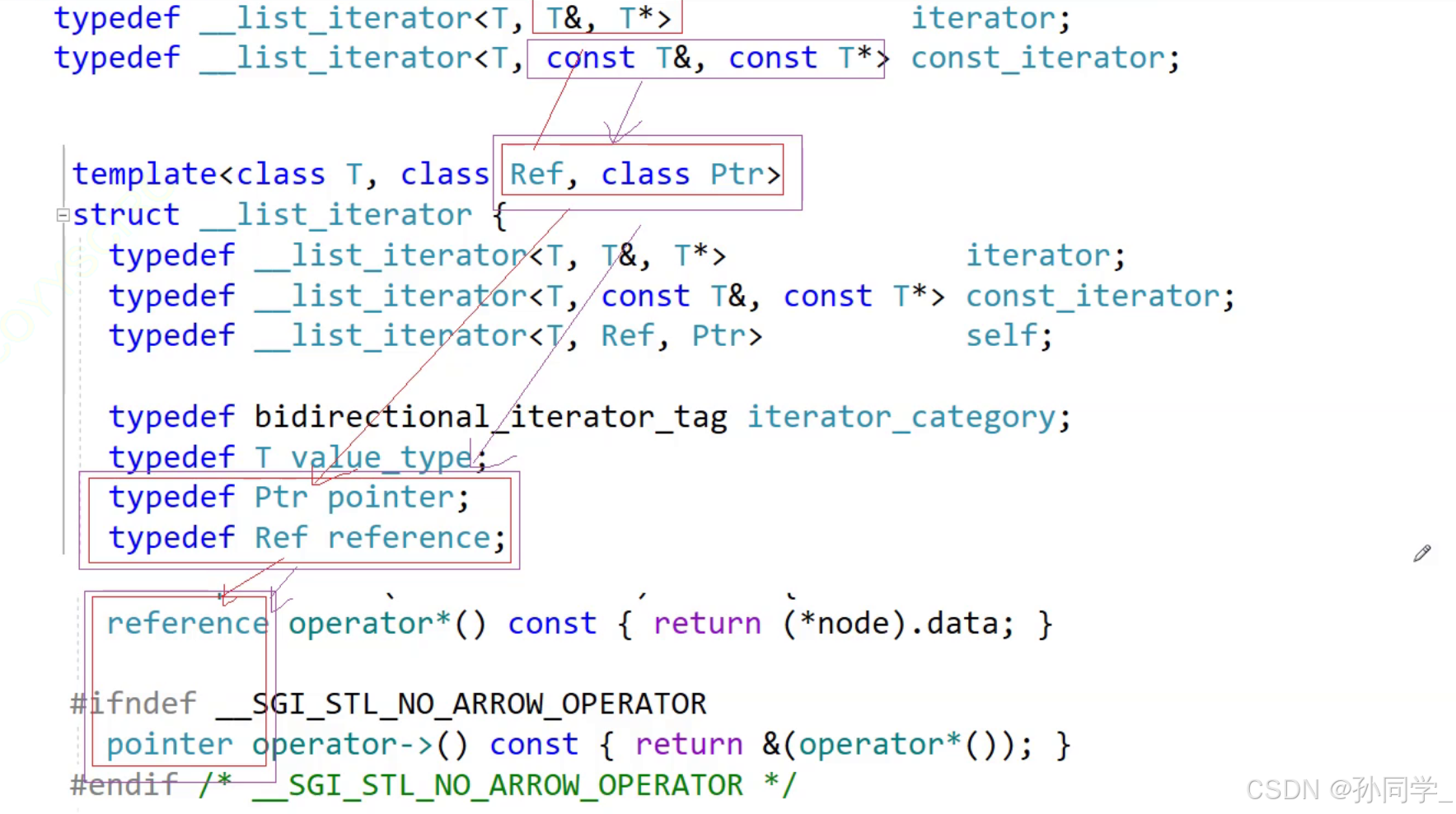
【C++】- 掌握STL List类:带你探索双向链表的魅力
文章目录 前言:一.list的介绍及使用1. list的介绍2. list的使用2.1 list的构造2.2 list iterator的使用2.3 list capacity2.4 list element access2.5 list modifiers2.6 list的迭代器失效 二.list的模拟实现1. list的节点2. list的成员变量3.list迭代器相关问题3.1…...

基于streamlit搭简易前端页面
前端小白第一次用streamlit搭简易页面,记录一下。 一些tips 每次与页面进行交互,如点击按钮、上传文件等,streamlit就会重新运行整个页面的所有代码。如果在页面渲染前需要对上传文件做很复杂的操作,重新运行所有代码就会重复这…...

Harmony Next开发通过bindSheet绑定半模态窗口
示例概述 Harmony Next开发通过bindSheet绑定半模态窗口 知识点 半模态窗口父子组件传值 组件 LoginComponent Component struct LoginComponent {// Prop 父子单项绑定值Prop message:string // Link 父子双向绑定值Link userName:stringLink password:stringLink isSh…...

YOLOv11改进,YOLOv11添加DLKA-Attention可变形大核注意力,WACV2024 ,二次创新C3k2结构
摘要 作者引入了一种称为可变形大核注意力 (D-LKA Attention) 的新方法来增强医学图像分割。这种方法使用大型卷积内核有效地捕获体积上下文,避免了过多的计算需求。D-LKA Attention 还受益于可变形卷积,以适应不同的数据模式。 理论介绍 大核卷积(Large Kernel Convolu…...

【51单片机】矩阵按键快速上手
51单片机矩阵按键是一种在单片机应用系统中广泛使用的按键排列方式,特别适用于需要多个按键但I/O口资源有限的情况。以下是对51单片机矩阵按键的详细介绍: 一、矩阵按键的基本概念 定义:矩阵按键,又称行列键盘,是…...

一文说清:git reset HEAD原理
1 使用add命令,将文件添加到暂存区 命令如下: 对比结果如下: 2 使用reset HEAD命令 如下: 结果对比如下: 忽略logs目录下的内容。 发现只是修改了index暂存区的内容。删掉了原来添加到暂存区的对象ID&#x…...

【前端面试题】书、定位问题、困难
看过什么书 《JavaScript 高级程序设计(第 4 版)》(作者:Matt Frisbie) 这是一本深入学习 JavaScript 语言的经典书籍。它详细地涵盖了 JavaScript 的高级特性,包括原型链、闭包、异步编程等复杂概念。以闭…...

WADesk 升级 Webpack5 一些技术细节认识5和4的区别在哪里
背景 升级过程中发现有很多新的知识点,虽然未来可能永远都不会再遇到,但是仍然是一次学习的好机会,可以让自己知道,打包软件的进化之路,和原来 Webpack 4 版本的差异在哪里。 移除的依赖记录 babel/register: 在 Nod…...

学习 Dockerfile 常用指令
学习 Dockerfile 常用指令 在构建 Docker 镜像时,Dockerfile 文件是一份至关重要的配置文件,它定义了构建镜像的所有步骤。通过在 Dockerfile 中使用不同的指令(命令),我们可以控制镜像的构建过程、设置环境、指定执行…...

day11 性能测试(3)——Jmeter 断言+关联
【没有所谓的运气🍬,只有绝对的努力✊】 目录 1、复习 2、查看结果树 多个http请求原因分析 3、作业 4、Jmeter断言 4.1 响应断言 4.1.1 案例 4.1.2 小结 4.2 json断言 4.2.1 案例 4.2.2 小结 4.3 断言持续时间 4.3.1 案例 4.3.2 小结 4.…...

ES6中的map和set
Map JS的数据对象(Obejct),本质上是键值对的集合(Hash结构),但是传统上只能用字符串当作键(一定程度上对其的使用有限制) 比如下面代码 const data {} const element document.…...

UE5中实现Billboard公告板渲染
公告板(Billboard)通常指永远面向摄像机的面片,游戏中许多技术都基于公告板,例如提示拾取图标、敌人血槽信息等,本文将使用UE5和材质节点制作一个公告板。 Gif效果: 网格效果: 1.思路 通过…...

泊松编辑 possion editing图像合成笔记
开源地址: GitHub - kono-dada/Reproduction-of-possion-image-editing 掩码必须是矩形框...

#渗透测试#漏洞挖掘#红蓝攻防#SRC漏洞挖掘
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
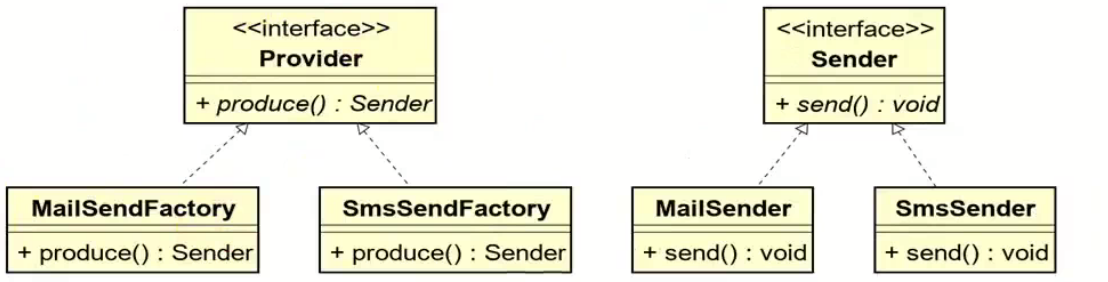
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
