蓝桥杯——竞赛省赛国赛题分享
目录
一.[蓝桥杯 2013 省 AB] 错误票据
代码如下:
二.[蓝桥杯 2024 省 Java B] 报数游戏
代码如下:
讲解:
三.[蓝桥杯 2014 国 C] 拼接平方数
代码如下:
四.三步问题(递归,上台阶)
代码1(不用递归)
代码2(使用递归)
该代码特色:
往期回顾:
一.[蓝桥杯 2013 省 AB] 错误票据


代码如下:
代码如下:
#include <stdio.h>
int main()
{int n = 0, i = 0, j = 0;int g[10005];scanf("%d", &n);while (scanf("%d", &g[i]) != EOF){i++;}int len = i;
//冒泡排序for (i = 0; i < len - 1; i++){for (j = i + 1; j < len; j++){if (g[i] > g[j]){int t = g[i];g[i] = g[j];g[j] = t;}}}int ans1 = 0, ans2 = 0;for (i = 0; i < len; i++){if (g[i + 1] - g[i] == 2)ans1 = g[i] + 1;if (g[i] == g[i + 1])ans2 = g[i];}printf("%d %d", ans1, ans2);return 0;
}
虽然是二维数组,但是可以看成一维,
题解中冒泡排序是解答关键!!!!!!
二.[蓝桥杯 2024 省 Java B] 报数游戏

代码如下:
int gcd(int a, int b)
{long long temp;long long temp1;long long n ;while (b != 0){n = a % b;temp = a;a = b;b = temp;temp1 = b;b = n;n = temp1;}return a;
}
int main()
{long long n = 0;n = 20*24/gcd(20, 24);long long m = 202420242024 / 10*n;long long i = 0;while (i<5){if (m % 20 == 0 || m % 24 == 0){i++;}m ++;}m--;printf("%lld", m);return 0;
}
讲解:
先通过gcd函数(辗转相除法)求出最大公约数,再利用公式a * b / gcd(a, b)求出最小公倍数,20 和 24 的最小公倍数是 120。
这意味着每 120 个数里,是 20 或 24 倍数的数有一定规律且数量是固定的。在区间[1, 120]内,是 20 倍数的数有120 / 20 = 6个(分别是 20、40、60、80、100、120),是 24 倍数的数有120 / 24 = 5个(分别是 24、48、72、96、120),但其中 120 重复计算了一次,所以在每 120 个数里,满足条件的数共有6 + 5 - 1 = 10个。
- 批量计算
利用这个规律,可以批量跳过一些区间来快速逼近第 202420242024 个符合要求的数。比如,已经知道每 120 个数里有 10 个符合要求的数,那么可以先计算出完整的 “120 个数区间” 的个数,即202420242024 / 10 = 20242024202(这里只取整数部分)个这样的区间。
这意味着前面已经处理了20242024202 * 120 = 2429042904240个数,此时还剩下一定数量的数要继续找,可以通过202420242024 % 10算出还需要在后续区间里找几个符合要求的数(余数为 4,表示还需要找 4 个)。
然后从2429042904240 + 1开始继续按顺序找剩下的数,直到找到 4 个符合要求的数为止,这样相比逐个数字去判断是否符合要求,可以大大减少循环次数,节省时间。
细节问题!!!:
循环结束m--;当i符合条件的时候,m会又自增一下。
虽然要再找4个,但是要i<5,因为开始进入一定符合但是不能算起始那个,因此要循环五次
三.[蓝桥杯 2014 国 C] 拼接平方数

代码如下:
#include <stdio.h>
#include <math.h>
#include <stdlib.h>// 计算数字的位数
int slen(int n)
{int len = 0;while (n > 0){n = n / 10;len++;}return len;
}// 判断一个数是否为拼接平方数
int is_spliced_square(int num)
{int len = slen(num);for (int split_pos = 1; split_pos < len; split_pos++){// 分割数字为两部分int part1 = num / (int)pow(10, split_pos);int part2 = num % (int)pow(10, split_pos);// 排除 0、00 等无效数字情况if (part1 == 0 || part2 == 0){continue;}int part1_sqrt = (int)sqrt((double)part1);int part2_sqrt = (int)sqrt((double)part2);if (part1_sqrt * part1_sqrt == part1 && part2_sqrt * part2_sqrt == part2){return 1;}}return 0;
}int main()
{int a = 0;int b = 0;int i1 = 0;int i2 = 0;if (scanf("%d%d", &a, &b) != 2){printf("输入格式有误,请重新输入两个整数\n");return 1;}// 遍历区间内的所有数字进行判断并输出for (int i = a; i <= b; i++){i1 = (int)sqrt(i);if (i1 * i1 != i){continue;}else{if (is_spliced_square(i)){printf("%d\n", i);}}}return 0;
}(注意:拼接平方数首先自己得是平方数!!!)
四.三步问题(递归,上台阶)
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
提示:
- n范围在[1, 1000000]之间
核心思想:
当 n > 3 时,进入这个 for 循环,从 i = 4 开始,逐步计算上 i 阶楼梯的走法数量。
递推关系的核心在于 a = (s1 + s2 + s3) % 1000000007; 这一行。对于上 i 阶楼梯(i > 3),最后一步可能是走了 1 阶(那么前面 i - 1 阶的走法数量就是 s1)、走了 2 阶(前面 i - 2 阶的走法数量是 s2)或者走了 3 阶(前面 i - 3 阶的走法数量是 s3),根据加法原理,上 i 阶楼梯的总走法数量就是上 i - 1 阶、i - 2 阶、i - 3 阶楼梯走法数量之和,即 s1 + s2 + s3。同时,为了满足题目对结果取模的要求,这里直接对相加的结果取模 1000000007 后赋值给 a,a 就代表上 i 阶楼梯的走法数量(取模后)。
代码1(不用递归)
int waysToStep(int n){long long int s1=1,s2=2,s3=4,a=0,b,c;if(n<=3){switch(n){case 1:a=s1;break;case 2:a=s2;break;case 3:a = s3;break;}}else{for(int i=4;i<=n;i++){a = (s1+s2+s3)%1000000007;b = s3;s3 = a;c = s2;s2 = b;s1 = c;}}return a;}代码2(使用递归)
#include <stdio.h>
#include <stdlib.h>// 定义一个足够大的数组用于存储已经计算过的结果,避免重复计算,初始化为 -1 表示未计算过
long long int memo[1000001];// 递归函数结合记忆化来计算上n阶楼梯的走法数量,取模操作按照题目要求进行
long long int waysToStep(int n) {if (n == 1) return 1;if (n == 2) return 2;if (n == 3) return 4;// 如果已经计算过该值,直接返回存储的结果,避免重复计算if (memo[n]!= -1) return memo[n];long long int result = (waysToStep(n - 1) + waysToStep(n - 2) + waysToStep(n - 3)) % 1000000007;// 将计算结果存储到备忘录数组中memo[n] = result;return result;
}
int main() {// 初始化memo数组为 -1,表示都未计算过for (int i = 0; i < 1000001; i++) {memo[i] = -1;}int n = 61;long long int ways = waysToStep(n);printf("上 %d 阶楼梯的走法数量(取模后)为:%lld\n", n, ways);return 0;
}
该代码特色:
数组的记忆使用避免了代码重复运算
1. 为什么会出现重复计算(以纯递归情况分析)
在不使用数组进行优化的纯递归解决 “三步问题” 的过程中,存在大量重复的子问题计算。例如,当我们要计算 waysToStep(5) 时,按照递归关系:
隐藏过程
long long int result = (waysToStep(4) + waysToStep(3) + waysToStep(2)) % 1000000007;
需要先去计算 waysToStep(4),而计算 waysToStep(4) 时又会按照它的递归关系:
隐藏过程
long long int result = (waysToStep(3) + waysToStep(2) + waysToStep(1)) % 1000000007;
再次去计算 waysToStep(3) 和 waysToStep(2) 以及 waysToStep(1)。注意这里的 waysToStep(3) 和 waysToStep(2) 在计算 waysToStep(5) 时已经计算过一次了,但是纯递归的方式没办法记住这个结果,所以就会重复地去调用函数计算它们。
同样地,在后续计算更大的 n 值时,像 waysToStep(2) 和 waysToStep(3) 这样的基础子问题会被反复地计算很多很多次,随着 n 的增大,这种重复计算的次数会急剧增加,导致效率变得极低,白白浪费了很多计算资源。
(1)memo 数组的定义和初始化
首先,定义了一个数组 memo 来存储已经计算过的结果,代码如下:
展开过程
这里把 memo 数组的每个元素初始化为 -1,是为了表示对应位置(也就是对应 n 值)的上楼梯走法数量还没有被计算过,后续通过判断元素的值是否为 -1 就能知道是否需要重新计算。
(2)在递归计算过程中的使用
在 waysToStep 函数内部,每次要进行递归计算之前,会先检查 memo 数组中对应位置的值,代码如下:
隐藏过程
if (memo[n]!= -1) return memo[n];
这行代码的意思是,如果 memo[n] 的值不等于 -1,那就说明之前已经计算过了上 n 阶楼梯的走法数量,并且已经把结果存储在了 memo[n] 这个位置,此时就不需要再去重复地通过递归调用计算了,直接返回 memo[n] 存储的结果就行,这样就避免了重复计算已经算过的子问题。
而当发现 memo[n] 是 -1,也就是还没有计算过时,才会按照正常的递归关系去计算上 n 阶楼梯的走法数量,计算完之后,会把结果存储到 memo[n] 中,方便下次再遇到同样的 n 值时直接获取,代码如下:
隐藏过程
long long int result = (waysToStep(n - 1) + waysToStep(n - 2) + waysToStep(n - 3)) % 1000000007;
memo[n] = result;
return result;
通过这样的方式,在整个递归调用的过程中,对于每个 n 值,最多只需要计算一次其对应的上楼梯走法数量,后续再次需要这个值时,直接从 memo 数组中获取,大大减少了不必要的计算,提高了代码的执行效率,尤其是当 n 的值比较大或者频繁调用 waysToStep 函数时,这种优化效果会更加明显。
往期回顾:
C语言——结构体(超详解)-CSDN博客
C语言——判断输入字符串是否合法代码分享-CSDN博客
C语言——字符串指针变量与字符数组(易错分析)-CSDN博客
C语言——习题练习(一)-CSDN博客
C语言——海龟作图(对之前所有内容复习)_海龟图c语言-CSDN博客
C语言函数递归经典题型——汉诺塔问题_汉诺(hanoi)塔问题-CSDN博客
C语言算法经典基础题型——求一个数的回文数(两种方法)_c语言编程题回文数-CSDN博客
相关文章:

蓝桥杯——竞赛省赛国赛题分享
目录 一.[蓝桥杯 2013 省 AB] 错误票据 代码如下: 二.[蓝桥杯 2024 省 Java B] 报数游戏 代码如下: 讲解: 三.[蓝桥杯 2014 国 C] 拼接平方数 代码如下: 四.三步问题(递归,上台阶) 代码…...

企业内训|阅读行业产品运营实战训练营-某运营商数字娱乐公司
近日,TsingtaoAI公司为某运营商旗下数字娱乐公司组织的“阅读行业产品运营实战训练营”在杭州落下帷幕。此次训练营由TsingtaoAI资深互联网产品专家程靖主持。该公司的业务骨干——来自内容、市场、业务、产品与技术等跨部门核心岗位、拥有8-10年实战经验的中坚力量…...

低空无人机产教融合技术详解
低空无人机产教融合技术是将无人机技术与教育、产业深度融合的一种新型教育模式,旨在培养既具备理论知识又具备实践能力的无人机专业人才。以下是对这一技术的详细解析: 一、产教融合的背景与意义 1. 背景: 随着无人机技术的快速发展&#…...

springboot中Controller内文件上传到本地以及阿里云
上传文件的基本操作 <form action"/upload" method"post" enctype"multipart/form-data"> <h1>登录</h1> 姓名:<input type"text" name"username" required><br> 年龄…...

Chrome 132 版本开发者工具(DevTools)更新内容
Chrome 132 版本开发者工具(DevTools)更新内容 一、使用 Gemini 调试 Network、Source 和 Performance Chrome 131 可以使用 Gemini 调试 CSS,现在可以调试更多模块了 与元素面板中的右键菜单类似,要打开 AI 辅助面板并开始与 …...

使用Python从阿里云物联网平台获取STM32温度数据
在物联网(IoT)应用中,设备数据的采集与监控至关重要。本文将详细介绍如何使用Python从阿里云物联网平台获取STM32设备的温度数据。我们将从已有的Java代码出发,逐步将其转换为Python,并处理在过程中遇到的问题…...

Spring Boot 声明式事务
Spring Boot中的声明式事务管理主要通过Transactional注解来实现。以下是Transactional注解的一些关键用法和特性: 1. 启用事务管理 在Spring Boot应用中使用Transactional注解之前,需要在启动类或者配置类上添加EnableTransactionManagement注解来启用事…...

websocket 局域网 webrtc 一对一 多对多 视频通话 的示例
基本介绍 WebRTC(Web Real-Time Communications)是一项实时通讯技术,它允许网络应用或者站点,在不借助中间媒介的情况下,建立浏览器之间点对点(Peer-to-Peer)的连接,实现视频流和&am…...

uniapp-微信小程序调用摄像头
1.uniapp中的index.vue代码 <template><view class"content"><view class"container"><!-- 摄像头组件 --><camera id"camera" device-position"front" flash"off" binderror"onCameraErr…...

鸿蒙学习笔记:用户登录界面
文章目录 1. 提出任务2. 完成任务2.1 创建鸿蒙项目2.2 准备图片资源2.3 编写首页代码2.4 启动应用 3. 实战小结 1. 提出任务 本次任务聚焦于运用 ArkUI 打造用户登录界面。需呈现特定元素:一张图片增添视觉感,两个分别用于账号与密码的文本输入框&#…...

无人机航测系统技术特点!
一、无人机航测系统的设计逻辑 无人机航测系统的设计逻辑主要围绕实现高效、准确、安全的航空摄影测量展开。其设计目标是通过无人机搭载相机和传感器,利用先进的飞行控制系统和数据处理技术,实现对地表信息的全方位、高精度获取。 需求分析࿱…...

《算法ZUC》题目
判断题 ZUC算法LFSR部分产生的二元序列具有很低的线性复杂度。 A.正确 B.错误 正确答案A 单项选择题 ZUC算法驱动部分LFSR的抽头位置不包括( )。 A.s15 B.s10 C.s7 D.s0 正确答案C 单项选择题 ZUC算法比特重组BR层主要使用了软件实现友好的…...

配置flutter 解决andriod studio报错 no device selected
flutter配置好后 明明下载好了模拟器 但是在andriod studio 找不到设备 显示no devices 这个时候需要我们配置一下flutter关联的android sdk的路径和文件夹 就可以解决了 flutter config --android-sdk 自己android studio的路径 这样配置就可以解决了~...

docker搭建Redis集群及哨兵(windows10环境,OSS Cluster)
一、基本概念 Redis:即 "Remote DIctionary Server" ,翻译为“远程字典服务器”。从字面意义上讲,它指的是一个远程的字典服务,意味着它是一个可以远程访问的服务,主要用于存储键值对(key-value pairs&…...
)
信息化基础知识——数字政府(山东省大数据职称考试)
大数据分析应用-初级 第一部分 基础知识 一、大数据法律法规、政策文件、相关标准 二、计算机基础知识 三、信息化基础知识 四、密码学 五、大数据安全 六、数据库系统 七、数据仓库. 第二部分 专业知识 一、大数据技术与应用 二、大数据分析模型 三、数据科学 数字政府 大数…...
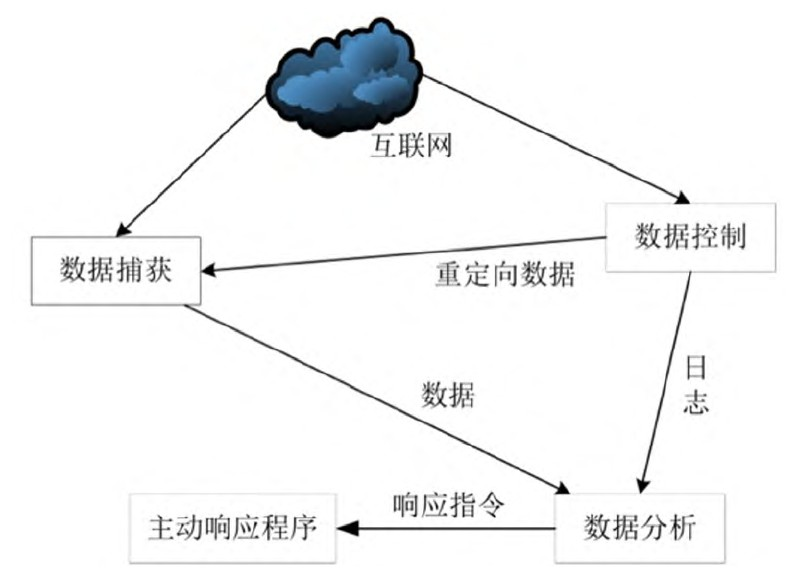
信息安全实训室网络攻防靶场实战核心平台解决方案
一、引言 网络安全靶场,作为一种融合了虚拟与现实环境的综合性平台,专为基础设施、应用程序及物理系统等目标设计,旨在向系统用户提供全方位的安全服务,涵盖教学、研究、训练及测试等多个维度。随着网络空间对抗态势的日益复杂化…...

Nginx主要知识点总结
1下载nginx 到nginx官网nginx: download下载nginx,然后解压压缩包 然后双击nginx.exe就可以启动nginx 2启动nginx 然后在浏览器的网址处输入localhost,进入如下页面说明nginx启动成功 3了解nginx的配置文件 4熟悉nginx的基本配置和常用操作 Nginx 常…...

PySide6程序框架设计
pyside6有一个优点自动适配高分辨ui pyqt5需要自己写这部分逻辑 1、主程序代码 DINGSHI01Main.py # -*- coding: utf-8 -*- import sys,time,copy from PySide6.QtWidgets import QWidget,QApplication from PySide6.QtCore import Qt from PySide6 import QtCore, QtGui, Q…...

「九」HarmonyOS 5 端云一体化实战项目——「M.U.」应用云侧开发云数据库
1 立意背景 M. 代表 “我”,U. 代表 “你”,这是一款用于记录情侣从相识、相知、相恋、见家长、订婚直至结婚等各个阶段美好记忆留存的应用程序。它旨在为情侣们提供一个专属的空间,让他们能够将一路走来的点点滴滴,如初次相遇时…...

记录:virt-manager配置Ubuntu arm虚拟机
virt-manager(Virtual Machine Manager)是一个图形用户界面应用程序,通过libvirt管理虚拟机(即作为libvirt的图形前端) 因为要在Linux arm环境做测试,记录下virt-manager配置arm虚拟机的过程 先在VMWare中…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
