HCIA-Access V2.5_4_1_1路由协议基础_IP路由表
大型网络的拓扑结构一般会比较复杂,不同的部门,或者总部和分支可能处在不同的网络中,此时就需要使用路由器来连接不同的网络,实现网络之间的数据转发。
本章将介绍路由协议的基础知识、路由表的分类、静态路由基础与配置、VLAN间路由的原理。
你可以带着这些问题来学习:
什么是路由?如何配置静态路由?
目标
学完本课程后,你将能够:
- 了解路由协议的基础知识;
- 了解路由的分类;
- 掌握静态路由基础与配置;
- 掌握VLAN间路由的原理
在大型网络中,一般会配置动态路由协议,而接入网通常是部署在网络边缘,一般只只需要配置静态路由。
什么是路由?

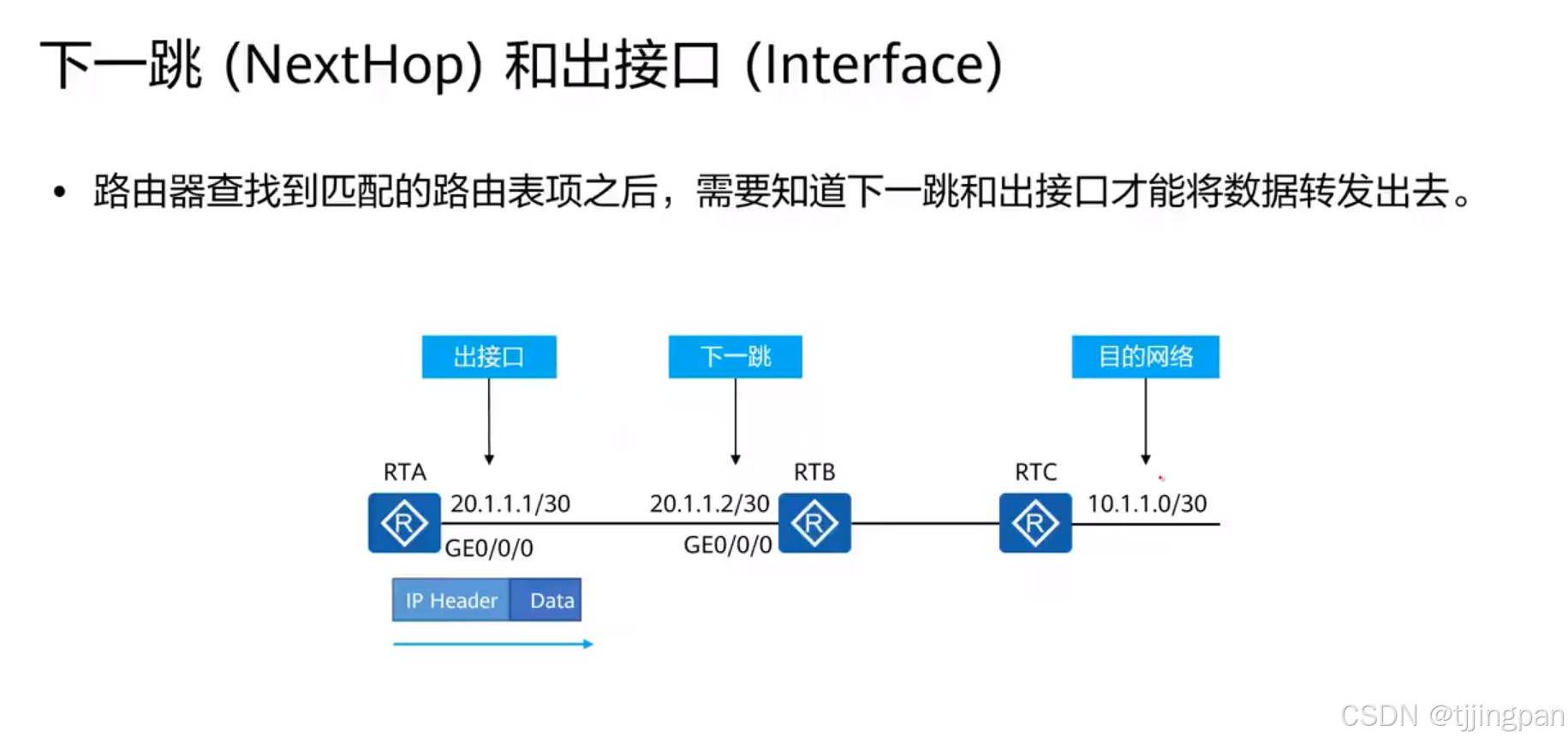
什么是路由呢? 路由就是指导IP报文发送的路径信息,指导IP报文如何从源端转发到目的地,如图,这个主机和这个主机想要远程通信,它可以通过上面这条路径转发到目的地,也可以通过中间这条链路发到目的地,也可以通过下面这条链路转发到目的地,那么路由器怎么走呢,这个时候就依靠路由表,路由器就会根据路由表来进行数据包的一个转发,同样,路由器也会根据自己的算法,选择一条它认为最优的路径,放在自己的IP路由表里面。
IP路由表

什么是路由表,它其实就是一张地图,告诉了我们如何去往目的地,那么里面具体包含了哪些参数,首先第一个就是目的地掩码,路由器收到报文之后就会查目的IP,看看有没有在我的路由表里面存在,如果存在就就可以进行转发,如果不存在,那么这个时候我就直接丢弃报文;第二个就是协议,这个就是路由的来源,这个路由条目可以是静态路由配置的,也可以是OSPF或者是RIP学习到的。它到底是通过哪一种路由协议学习到的,我们会在这边进行标识,第三个就是优先级,一般静态路由它的协议优先级是60,而RIP是100,OSPF是10,当然这个参数各个厂家是不一样的,这里说的是华为设备的优先级;第4个参数Cost值就是去往目的地需要的开销是多少,它会选择Cost值小的放在自己的路由表中;还有Flags,它会有两个参数,一个是R,一个是D,那么D代表它会把这条路由条目放入转发表中,按照这一条路由条目实现数据的一个转发,接着就是一下跳,那么就是去往目的地对端路由的接口地址;最后一个就是出接口,标识的你要去往目的地,应该从本地的哪一个接口转发出去,
路由的来源(Protocol)

最长匹配原则

路由优先级(Preference)

路由的度量(Metric)

下一跳(NextHop) 和出接口(Interface)
相关文章:

HCIA-Access V2.5_4_1_1路由协议基础_IP路由表
大型网络的拓扑结构一般会比较复杂,不同的部门,或者总部和分支可能处在不同的网络中,此时就需要使用路由器来连接不同的网络,实现网络之间的数据转发。 本章将介绍路由协议的基础知识、路由表的分类、静态路由基础与配置、VLAN间…...
Spring IOC 和 AOP的学习笔记
Spring框架是java开发行业的标准 Spring全家桶 Web:Spring Web MVC/Spring MVC、Spring Web Flux 持久层:Spring Data / Spring Data JPA 、Spring Data Redis 、Spring Data MongoDB 安全校验:Spring Security 构建工程脚手架ÿ…...

二七(vue2-03)、生命周期四个阶段及八个钩子、工程化开发和脚手架、组件注册、拆分组件
1. 生命周期 1.1 生命周期四个阶段 <!-- Vue生命周期:一个Vue实例从 创建 到 销毁 的整个过程。生命周期四个阶段:① 创建 ② 挂载 ③ 更新 ④ 销毁1.创建阶段:创建响应式数据2.挂载阶段:渲染模板3.更新阶段:修改…...

[树] 最轻的天平
问题描述 天平的两边有时不一定只能挂物品,还可以继续挂着另一个天平,现在给你一些天平的情况和他们之间的连接关系,要求使得所有天平都能平衡所需物品的总重量最轻。 一个天平平衡当且仅当“左端点的重量 \times 左端点到支点的距离 …...

Linux udev介绍使用
udev udev配置文件匹配键和赋值键操作符解释示例修改udev配置U盘自动挂载Usb卸载SD卡挂载SD卡卸载 udev配置文件 /etc/udev/udev.conf 这个文件通常很短,他可能只是包含几行#开头的注释,然后有几行选项: udev_root“/dev/” udev_rules“/…...
)
单片机:实现节日彩灯(附带源码)
本项目的目标是通过编程实现几个常见的彩灯效果,包括: 流水灯效果(从左到右或从右到左)闪烁效果(所有灯同时闪烁)渐变效果(灯光从亮到灭,再从灭到亮)定时切换颜色效果&a…...

流程引擎Activiti性能优化方案
流程引擎Activiti性能优化方案 Activiti工作流引擎架构概述 Activiti工作流引擎架构大致分为6层。从上到下依次为工作流引擎层、部署层、业务接口层、命令拦截层、命令层和行为层。 基于关系型数据库层面优化 MySQL建表语句优化 Activiti在MySQL中创建默认字符集为utf8&…...

【爬虫一】python爬虫基础合集一
【爬虫一】python爬虫基础合集一 1. 网络请求了解1.1. 请求的类型1.2. 网络请求协议1.3. 网络请求过程简单图解1.4. 网络请求Headers(其中的关键字释义):请求头、响应头 2. 网络爬虫的基本工作节点2.1. 了解简单网络请求获取响应数据的过程所涉及要点 1. 网络请求了…...

any/all 子查询优化规则的原理与解析 | OceanBase查询优化
背景 在通常情况下,当遇到包含any/all子查询的语句时,往往需要遵循嵌套执行的方式,因此其查询效率较低。Oceanbase中制定了相应的any/all子查询优化规则,能够能够识别并优化符合条件的any/all子查询,从而有效提升查询…...

ECharts 饼图:数据可视化的重要工具
ECharts 饼图:数据可视化的重要工具 引言 在数据分析和可视化的领域,ECharts 是一个广受欢迎的开源库。它由百度团队开发,用于在网页中创建交互式图表。ECharts 提供了多种图表类型,包括柱状图、折线图、散点图等,而饼图则是其中最常用的一种。本文将深入探讨 ECharts 饼…...

第10章:CSS最佳实践 --[CSS零基础入门]
代码组织 在CSS开发中,良好的代码组织和最佳实践对于项目的可维护性和扩展性至关重要。以下是两个示例,展示了如何遵循CSS最佳实践来组织代码。 示例 1: 使用 BEM(Block Element Modifier)命名法 BEM 是一种用于提高 CSS 可读性…...

怎么在idea中创建springboot项目
最近想系统学习下springboot,尝试一下全栈路线 从零开始,下面将叙述下如何创建项目 环境 首先确保自己环境没问题 jdkMavenidea 创建springboot项目 1.打开idea,选择file->New->Project 2.选择Spring Initializr->设置JDK->…...

递归读取指定目录下的文件
序言 需要读取sftp服务器上符合指定的文件名正则的文件列表,目前想到的最好的办法就是递归。 我这里引入的依赖是: <!-- jsch-sftp连接 --><dependency><groupId>com.jcraft</groupId><artifactId>jsch</artif…...

【模型压缩】原理及实例
在移动智能终端品类越发多样的时代,为了让模型可以顺利部署在算力和存储空间都受限的移动终端,对模型进行压缩尤为重要。模型压缩(model compression)可以降低神经网络参数量,减少延迟时间,从而实现提高神经…...

常用的JVM启动参数有哪些?
大家好,我是锋哥。今天分享关于【常用的JVM启动参数有哪些?】面试题。希望对大家有帮助; 常用的JVM启动参数有哪些? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 JVM(Java Virtual Machine)启…...

Curvelet 变换与FDCT
Curvelet变换 Curvelet变换 是一种多尺度、多方向的信号分析工具,专门用于处理具有各向异性特征的信号,例如边缘和曲线。与传统的傅里叶变换和小波变换相比,Curvelet变换能够更精确地表示信号中的曲线特征,因此在图像处理、地震数据分析、医学成像等领域得到了广泛应用。 …...
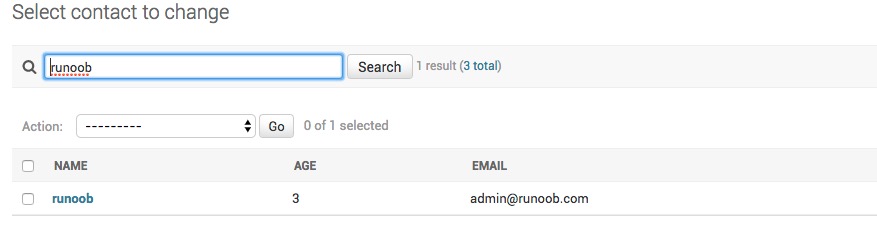
Django Admin 管理工具
Django 提供了基于 web 的管理工具。 Django 自动管理工具是 django.contrib 的一部分。你可以在项目的 settings.py 中的 INSTALLED_APPS 看到它: /HelloWorld/HelloWorld/settings.py 文件代码: INSTALLED_APPS ( django.contrib.admin, django.co…...

Android笔记【19】
具体示例 run: val result someObject.run {// 这里可以使用 thisthis.someMethod() }let: val result someObject?.let {// 这里使用 itit.someMethod() }with: val result with(someObject) {// 这里使用 thissomeMethod() }apply: val obj SomeClass().apply {// 这里使…...
矩阵在资产收益(Asset Returns)中的应用:以资产回报矩阵为例(中英双语)
本文中的例子来源于: 这本书,网址为:https://web.stanford.edu/~boyd/vmls/ 矩阵在资产收益(Asset Returns)中的应用:以资产回报矩阵为例 在量化金融中,矩阵作为一种重要的数学工具,被广泛用于描述和分析…...

Docker 中如何限制CPU和内存的使用 ?
在容器化的动态世界中,Docker 已经成为构建、部署和管理容器化的关键工具应用。然而,Docker 的效率在很大程度上取决于资源管理得有多好。设置适当的内存和 CPU 限制对于优化 Docker 性能至关重要,确保每个容器在不使主机负担过重的情况下获得…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
