全脐点曲面当且仅当平面或者球面的一部分
S 是全脐点曲面当且仅当 S 是平面或者球面的一部分。 S_\text{ 是全脐点曲面当且仅当 }{S_\text{ 是平面或者球面的一部分。}} S 是全脐点曲面当且仅当 S 是平面或者球面的一部分。
证:
充分性显然,下证必要性。
若 r ( u , v ) r(u,v) r(u,v)是全脐点曲面,设其在 ( u , v ) (u,v) (u,v)处的主曲率为 k ( u , v ) k(u,v) k(u,v),则有 L = k E , M = k F , N = k G L=kE,M=kF,N=kG L=kE,M=kF,N=kG。
则 k = L / E k=L/E k=L/E是光滑的,并且
⟨ n u + k r u , r u ⟩ = − L + k E = 0 \langle n_u+kr_u,r_u\rangle=-L+kE=0 ⟨nu+kru,ru⟩=−L+kE=0
⟨ n u + k r u , r v ⟩ = − M + k F = 0 ⟨ n u + k r u , n ⟩ = 0 \begin{aligned}&\langle n_u+kr_u,r_v\rangle=-M+kF=0\\&\langle n_u+kr_u,n\rangle=0\end{aligned} ⟨nu+kru,rv⟩=−M+kF=0⟨nu+kru,n⟩=0
从而 n u + k r u = 0 n_u+kr_u=0 nu+kru=0,同理 n v + k r v = 0 n_v+kr_v=0 nv+krv=0。
两式求偏导数再相减,得到 k v r u − k u r v = 0 k_vr_u-k_ur_v=0 kvru−kurv=0,从而 k u = k v = 0 k_u=k_v=0 ku=kv=0,从而 k k k是常值函数。
分两种情况讨论
1. k = 0 k=0 k=0,则带入上式看出 n n n是常向量,从而 S S S是平面;
2. k ≠ 0 k\neq0 k=0,则 a : = n + k r a:=n+kr a:=n+kr是常向量,则 ∣ r − a k ∣ = ∣ k n ∣ = 1 ∣ k ∣ |r-\frac ak|=|\frac kn|=\frac1{|k|} ∣r−ka∣=∣nk∣=∣k∣1。从而 S S S是半径为 1 ∣ k ∣ \frac1{|k|} ∣k∣1的球面的一部分。
相关文章:

全脐点曲面当且仅当平面或者球面的一部分
S 是全脐点曲面当且仅当 S 是平面或者球面的一部分。 S_\text{ 是全脐点曲面当且仅当 }{S_\text{ 是平面或者球面的一部分。}} S 是全脐点曲面当且仅当 S 是平面或者球面的一部分。 证: 充分性显然,下证必要性。 若 r ( u , v ) r(u,v) r(u,v)是…...

CSS学习记录18
CSS渐变 CSS渐变您可以显示两种或多种指定颜色之间的平滑过渡。 CSS定义了两种渐变类型: 线性渐变(向下/向上/向左/向右/对角线)径向渐变(由其中心定义) CSS线性渐变 如需创建线性渐变,您必须至少两个色…...

实验13 C语言连接和操作MySQL数据库
一、安装MySQL 1、使用包管理器安装MySQL sudo apt update sudo apt install mysql-server2、启动MySQL服务: sudo systemctl start mysql3、检查MySQL服务状态: sudo systemctl status mysql二、安装MySQL开发库 sudo apt-get install libmysqlcli…...
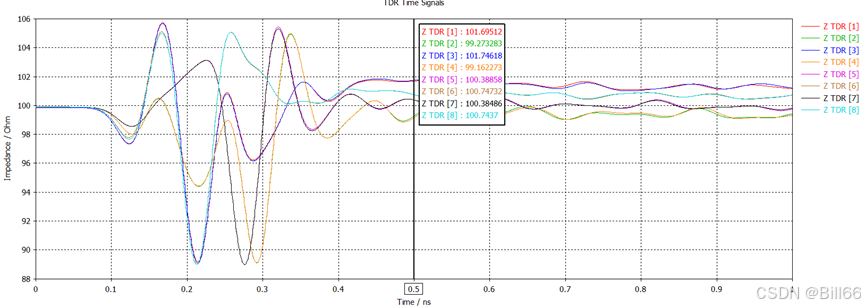
90度Floating B to B 高速连接器信号完整性仿真
在180度 B to B Connector 信号完整性仿真时,不会碰到端口设置不方便问题,但在做90度B to B Connector信号完整性仿真时就会碰到端口设置问题。如下面的90度B to B Connector。 公座 母座 公母对插后如下: 客户要求改Connector需符合PCI-E3.…...
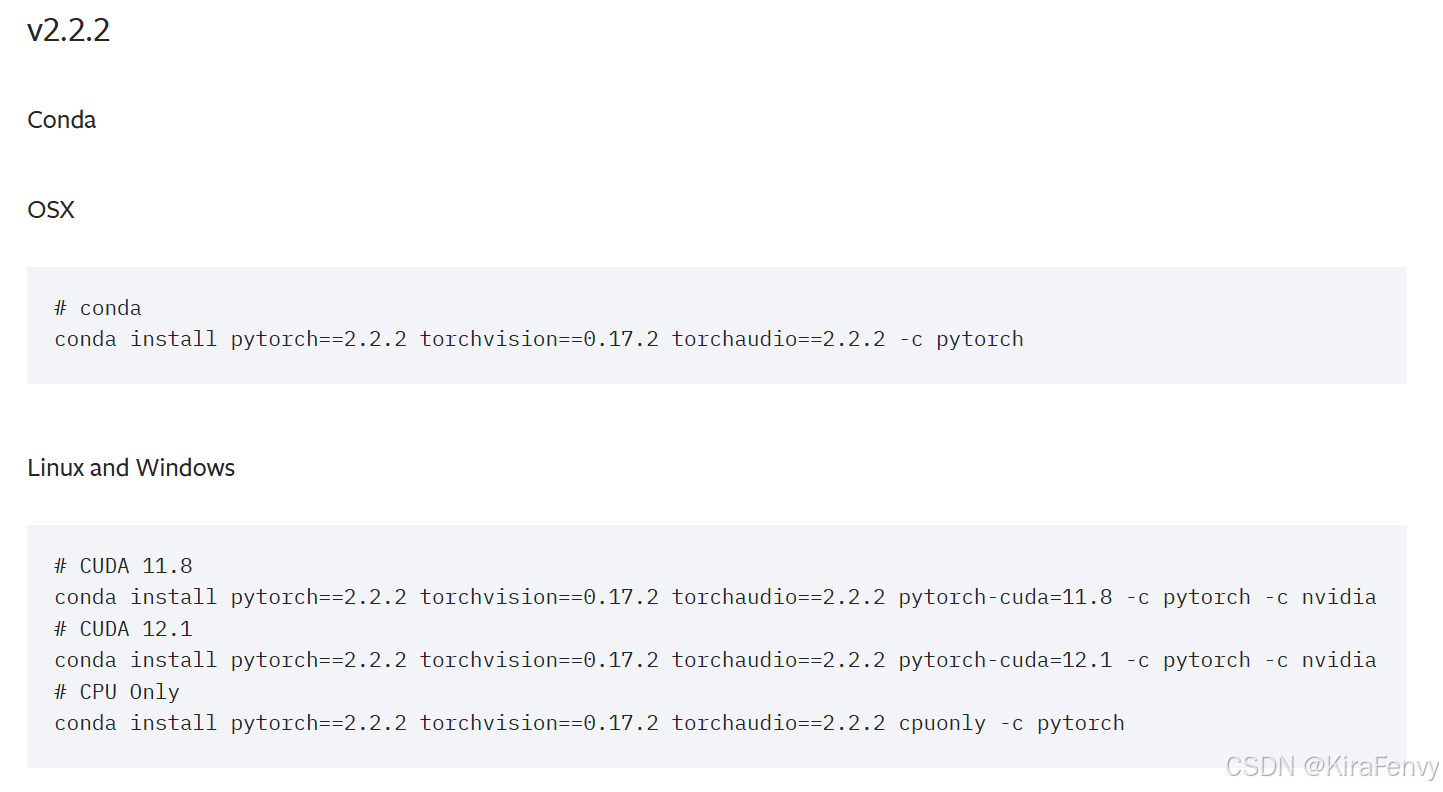
【踩坑】Pytorch与CUDA版本的关系及安装
Pytorch、CUDA和CUDA Toolkit区分 查看当前环境常用shell命令python脚本 Driver API CUDA(nvidia-smi)Runtime API CUDA(nvcc --version)pytorch选择CUDA版本的顺序安装需要的CUDA,多版本共存和自由切换 本文参考 http…...

信息隐藏 数字图像空域隐写与分析技术的实现
数字图像隐写与分析 摘要 随着信息技术的发展,隐写术作为一种信息隐藏技术,越来越受到关注。本文介绍了一种基于最低有效位(LSB)方法的数字图像隐写技术,并实现了隐写数据的嵌入与提取。通过卡方检验分析隐写图像的统计特性,评估隐写数据对图像的影响。实验结果表明,该…...

halcon单相机+机器人*眼在手外标定心得
目的 得到相机坐标系下的点与机器人底座base的转换关系,camera_in_base 两个不确定的定量 1,相机与机器人底座base之间的相对位置是固定的,既camera_in_base 2,机械手末端与标定物 tool_in_obj是固定的 辅助确定量 工作台与相…...

pytest入门十:配置文件
pytest.ini:pytest的主配置文件,可以改变pytest的默认行为conftest.py:测试用例的一些fixture配置 pytest.ini marks mark 打标的执行 pytest.mark.add add需要些marks配置否则报warning [pytest] markersadd:测试打标 测试用例中添加了 p…...
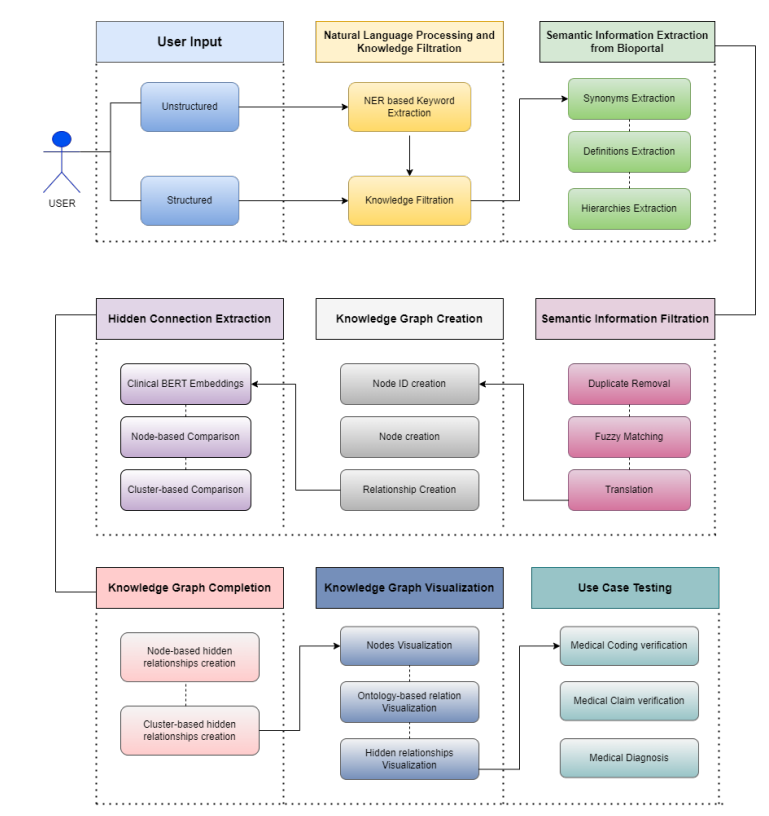
基于Clinical BERT的医疗知识图谱自动化构建方法,双层对比框架
基于Clinical BERT的医疗知识图谱自动化构建方法,双层对比框架 论文大纲理解1. 确认目标2. 目标-手段分析3. 实现步骤4. 金手指分析 全流程核心模式核心模式提取压缩后的系统描述核心创新点 数据分析第一步:数据收集第二步:规律挖掘第三步&am…...

介绍 Html 和 Html 5 的关系与区别
HTML(HyperText Markup Language)是构建网页的标准标记语言,而 HTML5 是 HTML 的最新版本,包含了一些新的功能、元素、API 和属性。HTML5 相对于早期版本的 HTML(比如 HTML4)有许多重要的改进和变化。以下是…...

C05S13-MySQL数据库备份与恢复
一、MySQL数据备份 1. 数据备份概述 数据备份的主要目的是灾难恢复,也就是当数据库等出现故障导致数据丢失,能够通过备份恢复数据。 数据备份可以分为物理备份和逻辑备份。物理备份,又称为冷备份,需要关闭数据库进行备份&#…...

【MySQL — 数据库基础】深入理解数据库服务与数据库关系、MySQL连接创建、客户端工具及架构解析
目录 1. 数据库服务&数据库&表之间的关系 1.1 复习 my.ini 1.2 MYSQL服务基于mysqld启动而启动 1.3 数据库服务的具体含义 1.4 数据库服务&数据库&表之间的关系 2. 客户端工具 2.1 客户端连接MySQL服务器 2.2 客…...
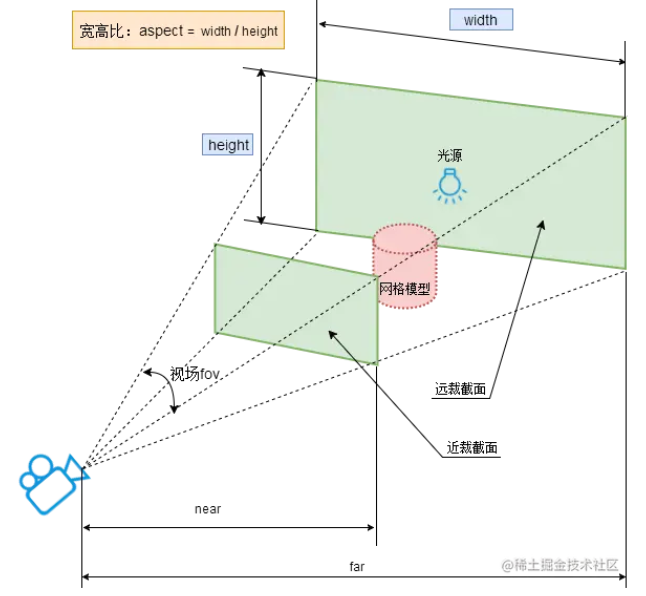
Three.js相机Camera控件知识梳理
原文:https://juejin.cn/post/7231089453695238204?searchId20241217193043D32C9115C2057FE3AD64 1. 相机类型 Three.js 主要提供了两种类型的相机:正交相机(OrthographicCamera)和透视相机(PerspectiveCamera&…...

Unity 开发Apple Vision Pro空间锚点应用Spatial Anchor
空间锚点具有多方面的作用 虚拟物体定位与固定: 位置保持:可以把虚拟物体固定在现实世界中的特定区域或位置。即使使用者退出程序后再次打开,之前锚定过的虚拟物体仍然能够出现在之前所锚定的位置,为用户提供连贯的体验。比如在一…...
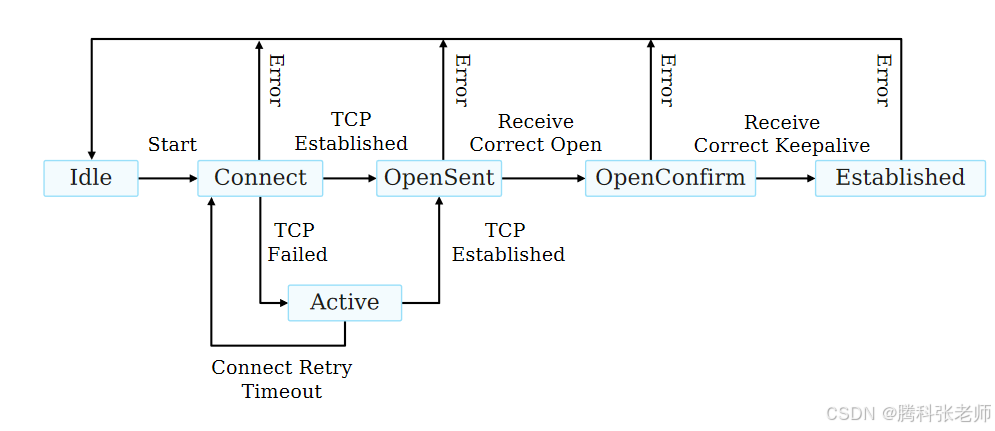
BGP的六种状态分别是什么?
此文章主要简单介绍下BGP的六种状态 1.Idle BGP会话的初始状态,路由器在此状态下不与任何BGP邻居通信,通常标识会话还没有开始或由于错误而未能启动,一般来说,缺乏去往BGP对等体的路由是导致BGP路由器其状态一直处于idle状态的常…...
IDEA搭建SpringBoot,MyBatis,Mysql工程项目
目录 一、前言 二、项目结构 三、初始化项目 四、SpringBoot项目集成Mybatis编写接口 五、代码仓库 一、前言 构建一个基于Spring Boot框架的现代化Web应用程序,以满足[公司/组织名称]对于[业务需求描述]的需求。通过利用Spring Boot简化企业级应用开发的优势&…...

Reactor
文章目录 正确的理解发送double free问题 1.把我们的reactor进行拆分2.链接管理3.Reactor的理论 listensock只需要设置_recv_cb,而其他sock,读,写,异常 所以今天写nullptr其实就不太对,添加为空就没办法去响应事件 获…...

在ESP32使用AT指令集与服务器进行TCP/IP通信时,<link ID> 解释
在ESP32使用AT指令集与服务器进行TCP/IP通信时,<link ID> 是一个非常重要的参数。它用于标识不同的连接实例,特别是在多连接场景下(如同时建立多个TCP或UDP连接)。每个连接都有唯一的<link ID>,通过这个ID…...

[SZ901] JTAG合并功能(类似FPGA菊花链)
SZ901 JTAG支持将JTAG端口组合,最多将四个JTAG变成一个 设置如下 Vivado 识别结果如下 两块板子,变成一组,,可以同时抓取信号,调试! SZ901 已上架淘宝,搜素“SZ901”哦...

paimon中的Tag
TAG 在传统数仓场景中,从传统数据库中导入的事实表数据一般是全量导入,按天分区每天都存储一份全量数据,paimon对此提供了Tag机制,创建TAG时,会对当前数据做一份全量快照,在之后对表的数据进行更新也不会影…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
