如何利用矩阵化简平面上的二次型曲线
二次型曲线的定义
在二维欧式平面上,一个二次型曲线都可以写成一个关于 x , y x,y x,y的二元二次多项式:
F ( x , y ) = a 11 x 2 + 2 a 12 x y + a 22 y 2 + 2 a 1 x + 2 a 2 y + a 0 = 0 \begin{equation} F(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2+2a_1x+2a_2y+a_0=0 \end{equation} F(x,y)=a11x2+2a12xy+a22y2+2a1x+2a2y+a0=0
其中 a 11 , a 22 , a 12 a_{11},a_{22},a_{12} a11,a22,a12不全为零。
当交叉项系数 a 12 a_{12} a12为零时,我们可以通过化简将二元二次多项式写为形如 ( x + α ) 2 a 2 ± ( y + β ) 2 b 2 = ± 1 \displaystyle \frac{(x+\alpha)^2}{a^2}\pm \frac{(y+\beta)^2}{b^2}=\pm 1 a2(x+α)2±b2(y+β)2=±1或 ( y + β ) 2 = ± 2 p ( x + α ) \displaystyle (y+\beta)^2=\pm 2p(x+\alpha) (y+β)2=±2p(x+α)这样的方程,这样就能够一目了然地看出曲线的类型是椭圆型、双曲线型还是抛物型。然而当交叉项系数 a 12 a_{12} a12不等于零时,我们往往无法一眼看出曲线的类型。因此一个很自然的问题是,如何通过平面上的线性变换,将多项式的交叉项消去,最终得到一个简洁的形式。本文将介绍这个方法。
将二次型曲线写成矩阵形式
首先我们需要将 ( 1 ) (1) (1)式改写成矩阵的形式,方便后续用矩阵对其进行线性变换。将多项式的二次项部分改写为:
φ ( x , y ) = a 11 x 2 + 2 a 12 x y + a 22 y 2 = ( x , y ) ( a 11 a 12 a 12 a 22 ) ( x y ) = ζ T Ω ζ \begin{equation} \varphi(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2=(x,y)\begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22}\end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}=\boldsymbol{\zeta^\mathrm{T} \Omega \zeta} \end{equation} φ(x,y)=a11x2+2a12xy+a22y2=(x,y)(a11a12a12a22)(xy)=ζTΩζ
其中 ζ = ( x , y ) T \boldsymbol{\zeta} = (x,y)^{\mathrm{T}} ζ=(x,y)T; Ω = ( a 11 a 12 a 12 a 22 ) \boldsymbol{\Omega}=\begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22}\end{pmatrix} Ω=(a11a12a12a22)是二次项 φ ( x , y ) \varphi(x,y) φ(x,y)的系数矩阵。
同样也将 F ( x , y ) F(x,y) F(x,y)改写成为矩阵的形式:
F ( x , y ) = ( x , y , 1 ) ( a 11 a 12 a 1 a 12 a 22 a 2 a 1 a 2 a 0 ) ( x y 1 ) = ( ζ T , 1 ) ( Ω κ κ T a 0 ) ( ζ 1 ) \begin{equation} F(x,y)=(x,y,1) \begin{pmatrix} a_{11} & a_{12} & a_1 \\ a_{12} & a_{22} & a_2 \\ a_1 & a_2 & a_0\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}= (\boldsymbol{\zeta}^{\mathrm{T}},1)\begin{pmatrix} \boldsymbol{\Omega} & \boldsymbol{\kappa} \\ \boldsymbol{\kappa}^{\mathrm{T}} & a_0 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta} \\ 1 \end{pmatrix} \end{equation} F(x,y)=(x,y,1) a11a12a1a12a22a2a1a2a0 xy1 =(ζT,1)(ΩκTκa0)(ζ1)
其中 κ = ( a 1 , a 2 ) T \boldsymbol{\kappa}=(a_1, a_2)^{\mathrm{T}} κ=(a1,a2)T; C = ( Ω κ κ T a 0 ) \boldsymbol{C}=\begin{pmatrix} \boldsymbol{\Omega} & \boldsymbol{\kappa} \\ \boldsymbol{\kappa}^{\mathrm{T}} & a_0 \end{pmatrix} C=(ΩκTκa0)是多项式 F ( x , y ) F(x,y) F(x,y)的系数矩阵。至此,我们将 ( 1 ) (1) (1)式改写成为了矩阵乘法的形式:
a 11 x 2 + 2 a 12 x y + a 22 y 2 + 2 a 1 x + 2 a 2 y + a 0 = ( ζ T , 1 ) ( Ω κ κ T a 0 ) ( ζ 1 ) = 0 \begin{equation} a_{11}x^2+2a_{12}xy+a_{22}y^2+2a_1x+2a_2y+a_0=(\boldsymbol{\zeta}^{\mathrm{T}},1)\begin{pmatrix} \boldsymbol{\Omega} & \boldsymbol{\kappa} \\ \boldsymbol{\kappa}^{\mathrm{T}} & a_0 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta} \\ 1 \end{pmatrix}=0 \end{equation} a11x2+2a12xy+a22y2+2a1x+2a2y+a0=(ζT,1)(ΩκTκa0)(ζ1)=0
通过转轴将交叉项系数消去
接下来我们尝试通过转轴矩阵消去二次曲线的交叉项。设转轴矩阵为 T = ( cos θ sin θ − sin θ cos θ ) \boldsymbol{T}=\begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{pmatrix} T=(cosθ−sinθsinθcosθ),则右手直角坐标系的转轴变换公式为:
ζ = T ζ ′ \begin{equation} \boldsymbol{\zeta}=\boldsymbol{T} \boldsymbol{\zeta'} \end{equation} ζ=Tζ′
其中 ζ ′ = ( x ′ , y ′ ) T \boldsymbol{\zeta'}=(x',y')^{\mathrm{T}} ζ′=(x′,y′)T。将 ( 5 ) (5) (5)式写成三维形式:
( ζ 1 ) = ( T 0 0 1 ) ( ζ ′ 1 ) \begin{equation} \begin{pmatrix}\boldsymbol{\zeta} \\ 1 \end{pmatrix} =\begin{pmatrix} \boldsymbol{T} & 0 \\ 0& 1 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta'} \\ 1 \end{pmatrix} \end{equation} (ζ1)=(T001)(ζ′1)
将 ( 6 ) (6) (6)代入 ( 4 ) (4) (4)式,得到:
( ζ T , 1 ) ( Ω κ κ T a 0 ) ( ζ 1 ) = ( ζ ′ T , 1 ) ( T T 0 0 1 ) ( Ω κ κ T a 0 ) ( T 0 0 1 ) ( ζ ′ 1 ) = ( ζ ′ T , 1 ) ( T T Ω T T T κ κ T T a 0 ) ( ζ ′ 1 ) = 0 \begin{equation} \begin{align} (\boldsymbol{\zeta}^{\mathrm{T}},1)\begin{pmatrix} \boldsymbol{\Omega} & \boldsymbol{\kappa} \\ \boldsymbol{\kappa}^{\mathrm{T}} & a_0 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta} \\ 1 \end{pmatrix} &=(\boldsymbol{\zeta'}^{\mathrm{T}},1)\begin{pmatrix} \boldsymbol{T^{\mathrm{T}}} & 0 \\ 0& 1 \end{pmatrix} \begin{pmatrix} \boldsymbol{\Omega} & \boldsymbol{\kappa} \\ \boldsymbol{\kappa}^{\mathrm{T}} & a_0 \end{pmatrix}\begin{pmatrix} \boldsymbol{T} & 0 \\ 0& 1 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta'} \\ 1 \end{pmatrix} \nonumber \\ &=(\boldsymbol{\zeta'}^{\mathrm{T}},1) \begin{pmatrix} \boldsymbol{T^{\mathrm{T}}} \boldsymbol{\Omega}\boldsymbol{T} & \boldsymbol{T^{\mathrm{T}}} \boldsymbol{\kappa} \\ \boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{T} & a_0 \end{pmatrix} \begin{pmatrix} \boldsymbol{\zeta'} \\ 1 \end{pmatrix} =0\nonumber \\ \end{align} \end{equation} (ζT,1)(ΩκTκa0)(ζ1)=(ζ′T,1)(TT001)(ΩκTκa0)(T001)(ζ′1)=(ζ′T,1)(TTΩTκTTTTκa0)(ζ′1)=0
比较 ( 4 ) (4) (4)与 ( 7 ) (7) (7),新的二次项系数矩阵变成了:
φ ( x ′ , y ′ ) = ( a 11 ′ a 12 ′ a 12 ′ a 22 ′ ) = T T Ω T \begin{equation} \varphi(x',y')=\begin{pmatrix} a_{11}' & a_{12}' \\ a_{12}' & a_{22}'\end{pmatrix}=\boldsymbol{T^{\mathrm{T}}} \boldsymbol{\Omega}\boldsymbol{T} \end{equation} φ(x′,y′)=(a11′a12′a12′a22′)=TTΩT
由于 T \boldsymbol{T} T是正交矩阵,因此有 T T T = I \boldsymbol{T}\boldsymbol{T^{\mathrm{T}}}=\boldsymbol{I} TTT=I。将 ( 8 ) (8) (8)式同时左乘 T \boldsymbol{T} T,得到:
Ω T = T ( a 11 ′ a 12 ′ a 12 ′ a 22 ′ ) \begin{equation} \boldsymbol{\Omega}\boldsymbol{T}=\boldsymbol{T}\begin{pmatrix} a_{11}' & a_{12}' \\ a_{12}' & a_{22}'\end{pmatrix} \end{equation} ΩT=T(a11′a12′a12′a22′)
我们希望经过转轴后交叉项系数为0,即 a 12 ′ = 0 a_{12}'=0 a12′=0。将转轴矩阵写成列向量形式 T = ( τ 1 , τ 2 ) \boldsymbol{T}=(\boldsymbol{\tau_1}, \boldsymbol{\tau_2}) T=(τ1,τ2),则 ( 9 ) (9) (9)式可以写为
Ω ( τ 1 , τ 2 ) = ( τ 1 , τ 2 ) ( a 11 ′ 0 0 a 22 ′ ) \begin{equation} \boldsymbol{\Omega}(\boldsymbol{\tau_1}, \boldsymbol{\tau_2})=(\boldsymbol{\tau_1}, \boldsymbol{\tau_2})\begin{pmatrix} a_{11}' & 0 \\0 & a_{22}'\end{pmatrix} \end{equation} Ω(τ1,τ2)=(τ1,τ2)(a11′00a22′)
展开后即得
Ω τ 1 = a 11 ′ τ 1 , Ω τ 2 = a 22 ′ τ 2 \begin{equation} \boldsymbol{\Omega}\boldsymbol{\tau_1}=a_{11}'\boldsymbol{\tau_1}, \boldsymbol{\Omega}\boldsymbol{\tau_2}=a_{22}'\boldsymbol{\tau_2} \end{equation} Ωτ1=a11′τ1,Ωτ2=a22′τ2
由 ( 11 ) (11) (11)式我们发现,当通过转轴消去交叉项系数 a 12 a_{12} a12时,新方程的 x ′ 2 , y ′ 2 x'^2,y'^2 x′2,y′2项系数恰好是原二次项系数矩阵 Ω \boldsymbol{\Omega} Ω的特征值,转轴矩阵的两个列向量是分别是特征值对应的特征向量。设 Ω \boldsymbol{\Omega} Ω的特征值分别是 ω 1 , ω 2 \omega_1, \omega_2 ω1,ω2,则消去交叉项后,二次项部分可以写为:
ω 1 x ′ 2 + ω 2 x ′ y \begin{equation} \omega_1 x'^2+ \omega_2 x'^y \end{equation} ω1x′2+ω2x′y
再次比较 ( 4 ) (4) (4)与 ( 7 ) (7) (7),新的一次项部分变成了
2 a 1 ′ x ′ + 2 a 2 ′ y ′ = 2 κ T T ζ ′ = 2 κ T ( τ 1 , τ 2 ) ( x ′ y ′ ) = 2 ( κ T τ 1 , κ T τ 2 ) ( x ′ y ′ ) = 2 κ T τ 1 x ′ + 2 κ T τ 2 y ′ \begin{equation} 2a'_1x'+2a'_2y' = 2\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{T}\boldsymbol{\zeta'} =2\boldsymbol{\kappa ^{\mathrm{T}}} (\boldsymbol{\tau_1}, \boldsymbol{\tau_2})\begin{pmatrix} x' \\ y' \end{pmatrix}=2(\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_1},\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_2})\begin{pmatrix} x' \\ y' \end{pmatrix}=2\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_1}x'+2\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_2}y' \end{equation} 2a1′x′+2a2′y′=2κTTζ′=2κT(τ1,τ2)(x′y′)=2(κTτ1,κTτ2)(x′y′)=2κTτ1x′+2κTτ2y′
综合 ( 12 ) , ( 13 ) (12),(13) (12),(13)式,我们最终得到了消除交叉项后的二次曲线方程:
a 11 ′ x ′ 2 + a 22 ′ y ′ 2 + 2 a 1 ′ x ′ + 2 a 2 ′ y ′ + a 0 = 0 \begin{equation} a'_{11} x'^2+ a'_{22} y'^2+2a'_1x'+2a'_2y'+a_0=0 \end{equation} a11′x′2+a22′y′2+2a1′x′+2a2′y′+a0=0
其中 a 11 ′ = ω 1 , a 22 ′ = ω 2 , a 1 ′ = κ T τ 1 , a 2 ′ = κ T τ 2 a'_{11}=\omega_1, a'_{22}=\omega_2,a'_1=\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_1}, a'_2=\boldsymbol{\kappa ^{\mathrm{T}}} \boldsymbol{\tau_2} a11′=ω1,a22′=ω2,a1′=κTτ1,a2′=κTτ2, ω 1 , τ 1 \omega_1, \boldsymbol{\tau_1} ω1,τ1与 ω 2 , τ 2 \omega_2, \boldsymbol{\tau_2} ω2,τ2是原二次项系数矩阵 Ω \boldsymbol{\Omega} Ω的特征值与特征向量。
通过移轴,进一步化简方程
根据系数符号不同,需要分以下集中情况讨论。
情况1:特征值 ω 1 , ω 2 \omega_1,\omega_2 ω1,ω2同号
此时得到的是椭圆型曲线。对 ( 14 ) (14) (14)式配方化简后得到
a 11 ′ ( x ′ + a 1 ′ a 11 ′ ) 2 + a 22 ′ ( y ′ + a 2 ′ a 22 ′ ) 2 + ( a 0 − a 1 ′ 2 a 11 ′ − a 2 ′ 2 a 22 ′ ) = 0 \displaystyle \begin{equation} a'_{11}(x'+\frac{a'_1}{ a'_{11}})^2+a'_{22}(y'+\frac{a'_2}{ a'_{22}})^2+(a_0-\frac{a'^2_1}{ a'_{11}}-\frac{a'^2_2}{ a'_{22}})=0 \end{equation} a11′(x′+a11′a1′)2+a22′(y′+a22′a2′)2+(a0−a11′a1′2−a22′a2′2)=0
对 ( 15 ) (15) (15)式进行移轴,令 x ′ ′ = x ′ + a 1 ′ a 11 ′ , y ′ ′ = y ′ + a 2 ′ a 22 ′ x''=x'+\dfrac{a'_1}{ a'_{11}},y''=y'+\dfrac{a'_2}{ a'_{22}} x′′=x′+a11′a1′,y′′=y′+a22′a2′,则上式可以写为:
a 11 ′ x ′ ′ 2 + a 22 ′ y ′ ′ 2 + c = 0 \displaystyle \begin{equation} a'_{11}x''^2+a'_{22}y''^2+c=0 \end{equation} a11′x′′2+a22′y′′2+c=0
其中 c = a 0 − a 1 ′ 2 a 11 ′ − a 2 ′ 2 a 22 ′ c=a_0-\dfrac{a'^2_1}{ a'_{11}}-\dfrac{a'^2_2}{ a'_{22}} c=a0−a11′a1′2−a22′a2′2。若 c ≠ 0 c\neq 0 c=0,将 c c c移至等号右侧,两边分别除以 − c -c −c得到:
x ′ ′ 2 − c / a 11 ′ + y ′ ′ 2 − c / a 22 ′ = 1 \displaystyle \begin{equation} \dfrac{x''^2}{-c/a'_{11}}+\dfrac{y''^2}{-c/a'_{22}}=1 \end{equation} −c/a11′x′′2+−c/a22′y′′2=1
此时若 c c c与 a 11 ′ a'_{11} a11′异号,则方程可以写为 x ′ ′ 2 ( − c / a 11 ′ ) 2 + y ′ ′ 2 ( − c / a 22 ′ ) 2 = 1 \dfrac{x''^2}{(\sqrt{-c/a'_{11}})^2}+\dfrac{y''^2}{(\sqrt{-c/a'_{22}})^2}=1 (−c/a11′)2x′′2+(−c/a22′)2y′′2=1,曲线是一个椭圆;若 c c c与 a 11 ′ a'_{11} a11′同号,则方程可以写为 x ′ ′ 2 ( c / a 11 ′ ) 2 + y ′ ′ 2 ( c / a 22 ′ ) 2 = − 1 \dfrac{x''^2}{(\sqrt{c/a'_{11}})^2}+\dfrac{y''^2}{(\sqrt{c/a'_{22}})^2}=-1 (c/a11′)2x′′2+(c/a22′)2y′′2=−1,曲线是一个虚椭圆(无轨迹)。若 c = 0 c=0 c=0,曲线退化为一个点,坐标为 ( − a 1 ′ a 11 ′ , − a 2 ′ a 22 ′ ) (-\dfrac{a'_1}{ a'_{11}},-\dfrac{a'_2}{ a'_{22}}) (−a11′a1′,−a22′a2′),恰好是移轴后的新坐标原点。
此时我们已经通过一次转轴,一次移轴得到了 ( 16 ) (16) (16)式,因此总的坐标变换公式为:
( x y ) = T ( x ′ ′ − a 1 ′ a 11 ′ y ′ ′ − a 2 ′ a 22 ′ ) = ( τ 1 x ′ ′ − τ 1 a 1 ′ a 11 ′ τ 2 y ′ ′ − τ 2 a 2 ′ a 22 ′ ) = T ( x ′ ′ y ′ ′ ) − T ′ \displaystyle \begin{equation} \begin{pmatrix} x \\ y \end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x''- \dfrac{a'_1}{ a'_{11}}\\ y''- \dfrac{a'_2}{ a'_{22}}\end{pmatrix}=\begin{pmatrix} \boldsymbol{\tau_1}x''-\boldsymbol{\tau_1} \dfrac{a'_1}{ a'_{11}}\\ \boldsymbol{\tau_2}y''-\boldsymbol{\tau_2} \dfrac{a'_2}{ a'_{22}} \end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x'' \\ y ''\end{pmatrix}-\boldsymbol{T'} \end{equation} (xy)=T x′′−a11′a1′y′′−a22′a2′ = τ1x′′−τ1a11′a1′τ2y′′−τ2a22′a2′ =T(x′′y′′)−T′
其中 T = ( τ 1 , τ 2 ) \boldsymbol{T}=(\boldsymbol{\tau_1}, \boldsymbol{\tau_2}) T=(τ1,τ2)是转轴矩阵, T ′ = ( a 1 ′ a 11 ′ τ 1 , a 2 ′ a 22 ′ τ 2 ) T \boldsymbol{T'}=( \dfrac{a'_1}{ a'_{11}}\boldsymbol{\tau_1} , \dfrac{a'_2}{ a'_{22}}\boldsymbol{\tau_2} )^{\mathrm{T}} T′=(a11′a1′τ1,a22′a2′τ2)T是移轴矩阵。
情况2:特征值 ω 1 , ω 2 \omega_1,\omega_2 ω1,ω2异号
此时得到的是双曲型曲线。用同样的方法对 ( 14 ) (14) (14)式移轴化简后得到
a 11 ′ x ′ ′ 2 + a 22 ′ y ′ ′ 2 + c = 0 \displaystyle \begin{equation} a'_{11}x''^2+a'_{22}y''^2+c=0 \end{equation} a11′x′′2+a22′y′′2+c=0
其中 c = a 0 − a 1 ′ 2 a 11 ′ − a 2 ′ 2 a 22 ′ c=a_0-\dfrac{a'^2_1}{ a'_{11}}-\dfrac{a'^2_2}{ a'_{22}} c=a0−a11′a1′2−a22′a2′2。根据 c c c不同分情况讨论,若 c c c与 a 11 ′ a'_{11} a11′异号,则方程可以写为 x ′ ′ 2 ( − c / a 11 ′ ) 2 − y ′ ′ 2 ( c / a 22 ′ ) 2 = 1 \dfrac{x''^2}{(\sqrt{-c/a'_{11}})^2}-\dfrac{y''^2}{(\sqrt{c/a'_{22}})^2}=1 (−c/a11′)2x′′2−(c/a22′)2y′′2=1,曲线是一个双曲线;若 c c c与 a 11 ′ a'_{11} a11′同号,则方程可以写为 y ′ ′ 2 ( − c / a 22 ′ ) 2 − x ′ ′ 2 ( c / a 11 ′ ) 2 = 1 \dfrac{y''^2}{(\sqrt{-c/a'_{22}})^2}-\dfrac{x''^2}{(\sqrt{c/a'_{11}})^2}=1 (−c/a22′)2y′′2−(c/a11′)2x′′2=1,曲线同样是一个双曲线。若 c = 0 c=0 c=0,此时曲线退化成为一对相交的直线。总的坐标变换公式仍然是 ( 18 ) (18) (18)式。
情况3:特征值 ω 1 , ω 2 \omega_1,\omega_2 ω1,ω2有且仅有一个为0
容易证得特征值不可能全为0,否则必有 a 11 = a 22 = 0 a_{11}=a_{22}=0 a11=a22=0,原方程不再是二次曲线。不妨设 ω 1 = a 11 = 0 \omega_1=a_{11}=0 ω1=a11=0,则 ( 14 ) (14) (14)可以改写为:
a 22 ′ ( y ′ + a 2 ′ a 22 ′ ) 2 + 2 a 1 ′ x ′ + c = 0 \begin{equation} a'_{22} (y' + \dfrac{a'_2}{a'_{22} })^2+2a'_1x'+c=0 \end{equation} a22′(y′+a22′a2′)2+2a1′x′+c=0
其中 c = a 0 − a 2 ′ 2 a 22 ′ c=a_0-\dfrac{a'^2_2}{a'_{22} } c=a0−a22′a2′2。
- 若 a 1 ′ ≠ 0 a'_{1}\neq 0 a1′=0,令 x ′ ′ = x ′ + a 0 a 22 ′ − a 2 ′ 2 2 a 1 ′ a 22 ′ , y ′ ′ = y ′ + a 2 ′ a 22 ′ x''=x'+\dfrac{a_{0}a'_{22}-a'^2_{2}}{2a'_{1}a'_{22}},y''=y'+\dfrac{a'_2}{ a'_{22}} x′′=x′+2a1′a22′a0a22′−a2′2,y′′=y′+a22′a2′,做移轴后的方程为:
y ′ ′ 2 = − 2 a 1 ′ a 22 ′ x ′ ′ \begin{equation} y''^2=\dfrac{-2a'_1}{a'_{22}}x'' \end{equation} y′′2=a22′−2a1′x′′
此时方程是一个抛物线方程,总的坐标变换公式为
( x y ) = T ( x ′ ′ − a 0 a 22 ′ − a 2 ′ 2 2 a 1 ′ a 22 ′ y ′ ′ − a 2 ′ a 22 ′ ) = T ( x ′ ′ y ′ ′ ) − ( a 0 a 22 ′ − a 2 ′ 2 2 a 1 ′ a 22 ′ τ 1 a 2 ′ a 22 ′ τ 2 ) \displaystyle \begin{equation} \begin{pmatrix} x \\ y \end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x''-\dfrac{a_{0}a'_{22}-a'^2_{2}}{2a'_{1}a'_{22}}\\ y''- \dfrac{a'_2}{ a'_{22}}\end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x'' \\ y ''\end{pmatrix}-\begin{pmatrix} \dfrac{a_{0}a'_{22}-a'^2_{2}}{2a'_{1}a'_{22}}\boldsymbol{\tau_1} \\ \dfrac{a'_2}{ a'_{22}} \boldsymbol{\tau_2}\end{pmatrix} \end{equation} (xy)=T x′′−2a1′a22′a0a22′−a2′2y′′−a22′a2′ =T(x′′y′′)− 2a1′a22′a0a22′−a2′2τ1a22′a2′τ2
- 若 a 1 ′ = 0 a'_{1}=0 a1′=0,令 x ′ ′ = x ′ , y ′ ′ = y ′ + a 2 ′ a 22 ′ x''=x', y''=y'+\dfrac{a'_2}{ a'_{22}} x′′=x′,y′′=y′+a22′a2′,做移轴后的方程为:
a 22 ′ y ′ ′ 2 + c = 0 \begin{equation} a'_{22}y''^2+c=0 \end{equation} a22′y′′2+c=0
若 c c c与 a 22 ′ a'_{22} a22′异号,则曲线是一对平行直线;若 c c c与 a 22 ′ a'_{22} a22′同号,曲线是一对虚直线(无轨迹);若 c = 0 c=0 c=0,则曲线是一对与 x x x轴重合的直线。此时总的坐标变换公式为:
( x y ) = T ( x ′ ′ y ′ ′ − a 2 ′ a 22 ′ ) = T ( x ′ ′ y ′ ′ ) − ( 0 a 2 ′ a 22 ′ τ 2 ) \displaystyle \begin{equation} \begin{pmatrix} x \\ y \end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x''\\ y''- \dfrac{a'_2}{ a'_{22}}\end{pmatrix}=\boldsymbol{T}\begin{pmatrix} x'' \\ y ''\end{pmatrix}-\begin{pmatrix}0 \\ \dfrac{a'_2}{ a'_{22}} \boldsymbol{\tau_2}\end{pmatrix} \end{equation} (xy)=T x′′y′′−a22′a2′ =T(x′′y′′)− 0a22′a2′τ2
总结
上文证明了,通过转轴矩阵和移轴矩阵,根据二次项系数特征值的不同,任意二次曲线都可以化简为三个大类,分别是椭圆型曲线、双曲型曲线以及抛物型曲线。其中椭圆形曲线可能对应椭圆、虚椭圆、一个点三种情况;双曲型曲线可能对应双曲线、一对交叉直线两种情况;抛物型曲线可能对应抛物线、一对平行直线、一对虚平行直线、一对重合直线四种情况。共计九种情形。
相关文章:

如何利用矩阵化简平面上的二次型曲线
二次型曲线的定义 在二维欧式平面上,一个二次型曲线都可以写成一个关于 x , y x,y x,y的二元二次多项式: F ( x , y ) a 11 x 2 2 a 12 x y a 22 y 2 2 a 1 x 2 a 2 y a 0 0 \begin{equation} F(x,y)a_{11}x^22a_{12}xya_{22}y^22a_1x2a_2ya_00…...
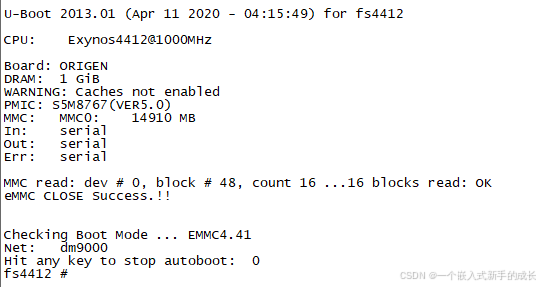
【系统移植】制作SD卡启动——将uboot烧写到SD卡
在开发板上启动Linux内核,一般有两种方法,一种是从EMMC启动,还有一种就是从SD卡启动,不断哪种启动方法,当开发板上电之后,首先运行的是uboot。 制作SD卡启动,首先要将uboot烧写到SD卡ÿ…...
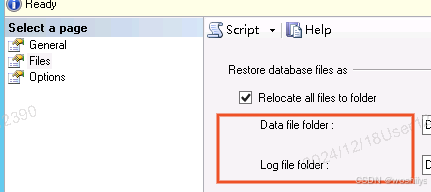
sql server 数据库还原,和数据检查
右键数据库选择还原, 还原的备份文件必须选择在本地的文件(远程文件没有试过)还原数据库名字可以修改,然后file选择中有个2个目录data file 的目录 ,和log data 的目录都可以重新选择还原到的新的目录,不要…...
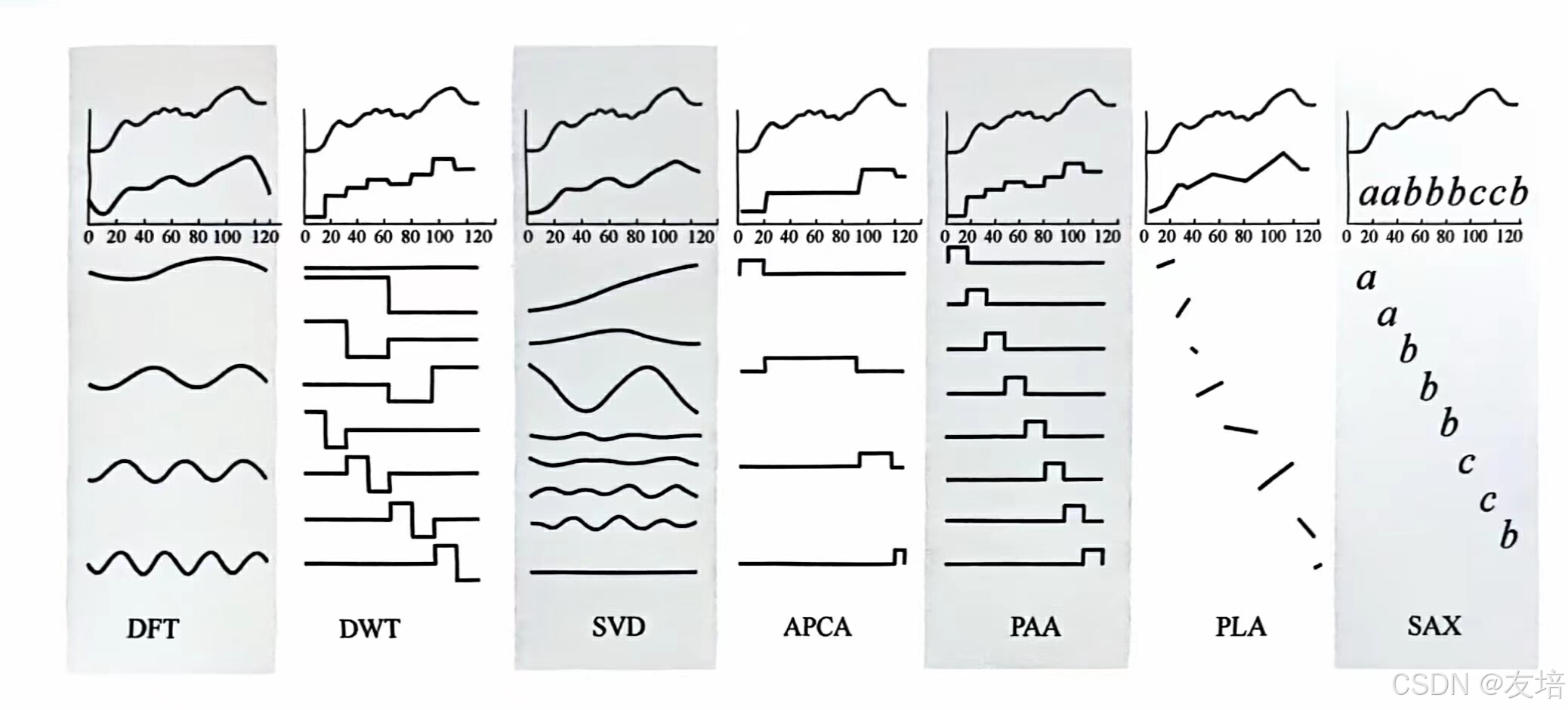
工业大数据分析算法实战-day12
文章目录 day12时序分解STL(季节性趋势分解法)奇异谱分析(SSA)经验模态分解(EMD) 时序分割ChangpointTreeSplitAutoplait有价值的辅助 时序再表征 day12 今天是第12天,昨天主要是针对信号处理算…...
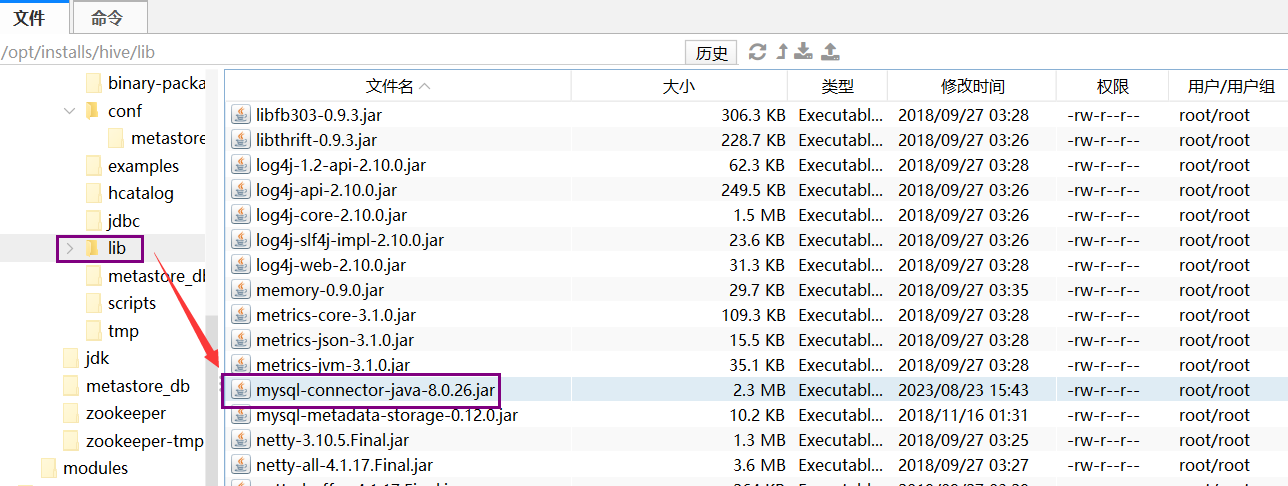
Hive其一,简介、体系结构和内嵌模式、本地模式的安装
目录 一、Hive简介 二、体系结构 三、安装 1、内嵌模式 2、测试内嵌模式 3、本地模式--最常使用的模式 一、Hive简介 Hive 是一个框架,可以通过编写sql的方式,自动的编译为MR任务的一个工具。 在这个世界上,会写SQL的人远远大于会写ja…...
LSTM-SVM时序预测 | Matlab基于LSTM-SVM基于长短期记忆神经网络-支持向量机时间序列预测
LSTM-SVM时序预测 | Matlab基于LSTM-SVM基于长短期记忆神经网络-支持向量机时间序列预测 目录 LSTM-SVM时序预测 | Matlab基于LSTM-SVM基于长短期记忆神经网络-支持向量机时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.LSTM-SVM时序预测 | Matlab基于LSTM…...

MacPorts 中安装高/低版本软件方式,以 RabbitMQ 为例
查询信息 这里以 RabbitMQ 为例,通过搜索得到默认安装版本信息: port search rabbitmq-server结果 ~/Downloads> port search rabbitmq-server rabbitmq-server 3.11.15 (net)The RabbitMQ AMQP Server ~/Downloads>获取二进制文件 但当前官网…...
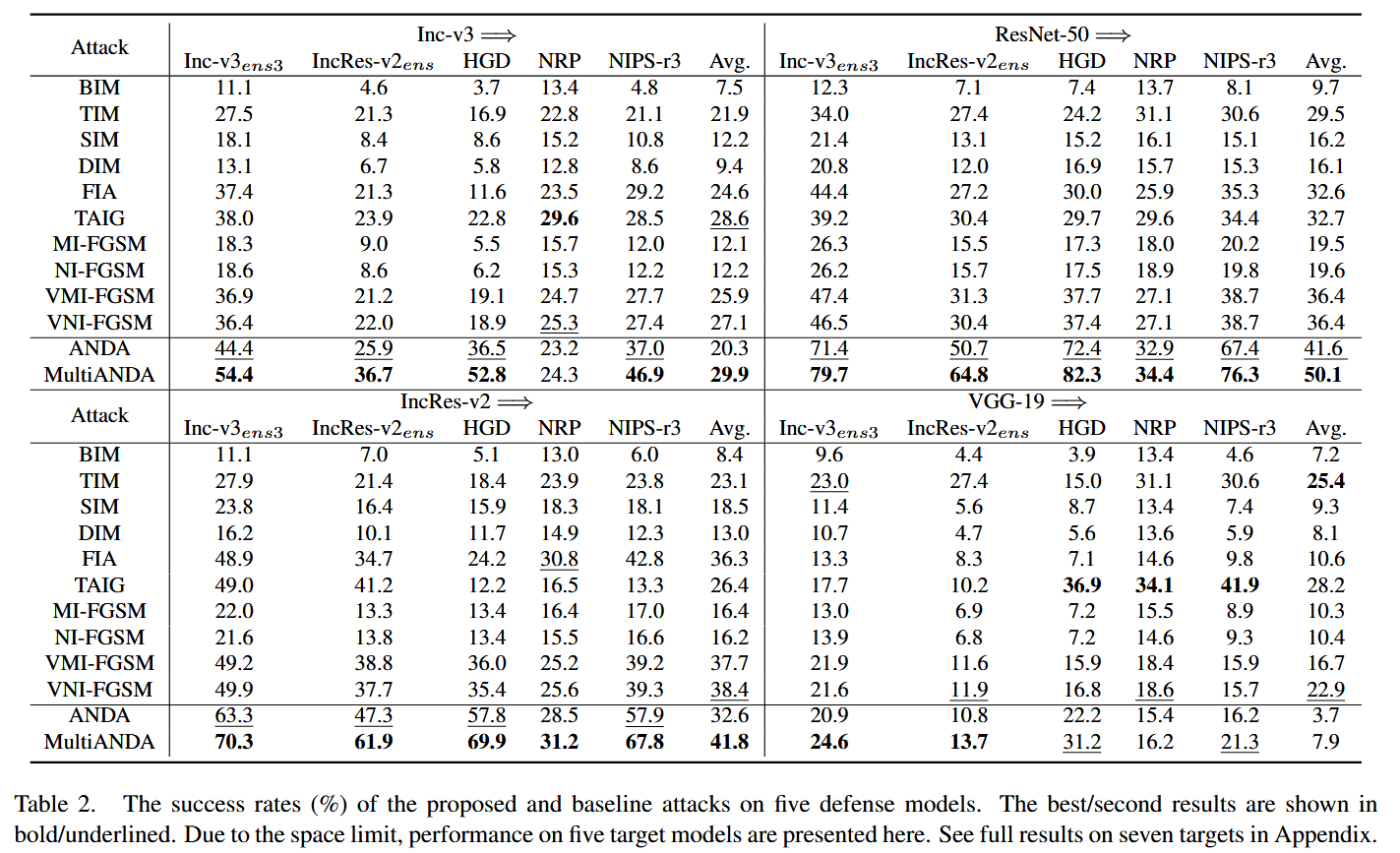
CVPR2024 | 通过集成渐近正态分布学习实现强可迁移对抗攻击
Strong Transferable Adversarial Attacks via Ensembled Asymptotically Normal Distribution Learning 摘要-Abstract引言-Introduction相关工作及前期准备-Related Work and Preliminaries1. 黑盒对抗攻击2. SGD的渐近正态性 提出的方法-Proposed Method随机 BIM 的渐近正态…...

建投数据与腾讯云数据库TDSQL完成产品兼容性互认证
近日,经与腾讯云联合测试,建投数据自主研发的人力资源信息管理系统V3.0、招聘管理系统V3.0、绩效管理系统V2.0、培训管理系统V3.0通过腾讯云数据库TDSQL的技术认证,符合腾讯企业标准的要求,产品兼容性良好,性能卓越。 …...

群晖利用acme.sh自动申请证书并且自动重载证书的问题解决
前言 21年的时候写了一个在群晖(黑群晖)下利用acme.sh自动申请Let‘s Encrypt的脚本工具 群晖使用acme自动申请Let‘s Encrypt证书脚本,自动申请虽然解决了,但是自动重载一直是一个问题,本人也懒,一想到去…...

质量小议51 - 茧房
茧房:茧房是指蚕茧所建的住所或空间,由一个蚕丝囊完全包裹住的一个密封的空间。 -- CSDN创作助手 信息茧房 - 指通过互联网和数字技术,将个人封闭在一个虚拟的信息环境中,使其只接收来自特定渠道的信息,而屏蔽其他信息…...

【C++图论】2359. 找到离给定两个节点最近的节点|1714
本文涉及知识点 C图论 打开打包代码的方法兼述单元测试 LeetCode2359. 找到离给定两个节点最近的节点 给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。 有向图用大小为 n 下标从 0 开始的数组 edges 表示,…...

重拾设计模式-外观模式和适配器模式的异同
文章目录 目的不同适配器模式:外观模式: 结构和实现方式不同适配器模式:外观模式: 对客户端的影响不同适配器模式:外观模式: 目的不同 适配器模式: 主要目的是解决两个接口不兼容的问题&#…...

51c自动驾驶~合集42
我自己的原文哦~ https://blog.51cto.com/whaosoft/12888355 #DriveMM 六大数据集全部SOTA!最新DriveMM:自动驾驶一体化多模态大模型(美团&中山大学) 近年来,视觉-语言数据和模型在自动驾驶领域引起了广泛关注…...

34 Opencv 自定义角点检测
文章目录 cornerEigenValsAndVecscornerMinEigenVal示例 cornerEigenValsAndVecs void cornerEigenValsAndVecs(InputArray src, --单通道输入8位或浮点图像OutputArray dst, --输出图像,同源图像或CV_32FC(6)int blockSize, --邻域大小值int ape…...

信创技术栈发展现状与展望:机遇与挑战并存
一、引言 在信息技术应用创新(信创)战略稳步推进的大背景下,我国信创技术栈已然在诸多关键层面收获了亮眼成果,不过也无可避免地遭遇了一系列亟待攻克的挑战。信创产业作为我国达成信息技术自主可控这一目标的关键一招,…...

跟我学c++中级篇——C++中的缓存利用
一、缓存 学习过计算机知识的一般都知道缓存这个概念,大约也知道缓存是什么。但是如果是程序员,如何更好的利用缓存,可能就有很多人不太清楚了。其实缓存的目的非常简单,就是了更高效的操作数据。大家都听说过“局部性原理”&…...

二叉树_堆
目录 一. 树(非线性结构) 1.1 树的概念与结构 1.2 树的表示 二. 二叉树 2.1 二叉树的概念与结构 2.2 特殊的二叉树 2.3 二叉树的存储结构 三. 实现顺序结构的二叉树 3.1 堆的概念与结构 一. 树(非线性结构) 1.1 树的概念与结构 概念ÿ…...

word文档中有大量空白行删除不掉,怎么办?
现象: 分页之间的空白行太多了( 按回车没用。删除也删除不掉 ) 解决办法: 按ctrl a 全选这个文档右击鼠标,点击【段落】选择【换行和分页】,然后把【分页】里的选项全部勾掉,然后点击【确定】…...

python rabbitmq实现简单/持久/广播/组播/topic/rpc消息异步发送可配置Django
windows首先安装rabbitmq 点击参考安装 1、环境介绍 Python 3.10.16 其他通过pip安装的版本(Django、pika、celery这几个必须要有最好版本一致) amqp 5.3.1 asgiref 3.8.1 async-timeout 5.0.1 billiard 4.2.1 celery 5.4.0 …...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
