代码随想录day23 | leetcode 39.组合总和 40.组合总和II 131.分割回文串
39.组合总和
Java
class Solution { List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates);backtracking(candidates,target,0,0);return result;}public void backtracking(int[] candidates,int target,int sum,int startIndex){if (sum>target){return;}if (sum == target){result.add(new LinkedList<>(path));return;}for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {path.add(candidates[i]);sum += candidates[i];backtracking(candidates,target,sum,i);sum -= candidates[i];path.removeLast();}}
}
回溯方法:backtracking
public void backtracking(int[] candidates, int target, int sum, int startIndex) {if (sum > target) { // 剪枝:如果当前和已经超过目标,直接返回return;}if (sum == target) { // 找到满足条件的组合result.add(new LinkedList<>(path)); // 保存当前路径到结果return;}for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {path.add(candidates[i]); // 做选择:将当前数字加入路径sum += candidates[i]; // 更新路径总和backtracking(candidates, target, sum, i); // 递归,允许重复选择当前数字sum -= candidates[i]; // 撤销选择:恢复之前的状态path.removeLast(); // 从路径中移除最后一个数字,回溯}
}
逻辑解释
- 递归终止条件
sum > target:当前路径总和超过目标值,停止递归。sum == target:找到一组符合条件的组合,将path复制加入结果。
- 循环递归
- 循环起点:从
startIndex开始,保证每次递归处理当前数字及其后续数字。 - 条件:
sum + candidates[i] <= target- 剪枝条件,提前终止无意义的递归。 - 允许重复选择:- 递归调用时仍从
i开始 (backtracking(candidates, target, sum, i)),因此当前数字可以重复加入组合。
- 循环起点:从
- 回溯过程
path.add(candidates[i])和path.removeLast():分别表示“选择当前数字”和“撤销选择”。sum += candidates[i]和sum -= candidates[i]:动态更新当前路径的总和。
40.组合总和II
树层去重一个数完整搜完一边,另一个重复的数不用搜第二遍
Java
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);boolean[] used = new boolean[candidates.length];Arrays.fill(used,false);backtracking(candidates,target,0,0,used);return result;}public void backtracking(int[] candidates, int target,int sum,int stateIndex,boolean[] used){if (sum>target){return;}if (sum == target){result.add(new ArrayList<>(path));}for (int i = stateIndex; i < candidates.length; i++) {if (i>0&&candidates[i-1]==candidates[i]&&used[i-1]==false){//重要,按层去重continue;}path.add(candidates[i]);sum += candidates[i];used[i] = true;backtracking(candidates,target,sum,i+1,used);path.removeLast();sum -= candidates[i];used[i] = false;}}
}
关键点
- 数组排序:
Arrays.sort(candidates);
对数组 candidates 进行排序是为了方便去重和剪枝。排序后,相同的元素会相邻,可以通过简单的逻辑避免重复。
- 去重逻辑:
if (i > 0 && candidates[i - 1] == candidates[i] && used[i - 1] == false) {continue;}
这一部分用于按“层”去重。如果当前元素与前一个元素相同,且前一个元素在当前层没有被使用(used[i - 1] == false),就跳过这个元素,避免重复组合。
- 递归与回溯:
- 递归条件:递归深入到下一层(选择下一个数字)。
- 回溯操作:撤销上一步的选择(移除当前路径中的数字,恢复
sum和used的状态)。
代码逻辑
全局变量
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
result:存储最终的所有满足条件的组合。path:存储当前递归路径上的数字组合。
主函数
public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates); // 排序,方便去重和剪枝boolean[] used = new boolean[candidates.length]; // 记录每个数字是否使用backtracking(candidates, target, 0, 0, used); // 初始状态return result;
}
- 对数组排序后,初始化
used数组为false。 - 调用回溯函数
backtracking开始寻找组合。
回溯函数
public void backtracking(int[] candidates, int target, int sum, int stateIndex, boolean[] used) {if (sum > target) {return; // 剪枝:当前组合和大于目标值}if (sum == target) {result.add(new ArrayList<>(path)); // 找到符合条件的组合,加入结果集return;}for (int i = stateIndex; i < candidates.length; i++) {if (i > 0 && candidates[i - 1] == candidates[i] && used[i - 1] == false) {continue; // 去重:跳过相同的元素}path.add(candidates[i]); // 添加当前数字到路径sum += candidates[i]; // 更新路径和used[i] = true; // 标记当前数字为已使用backtracking(candidates, target, sum, i + 1, used); // 递归到下一层path.removeLast(); // 回溯,撤销选择sum -= candidates[i]; // 恢复路径和used[i] = false; // 恢复使用状态}
}
重点逻辑
- 递归结束条件:
- 当
sum > target时,直接返回,表示当前路径无效。 - 当
sum == target时,说明找到一个符合条件的组合,将其加入result。
- 当
- 去重:
if (i > 0 && candidates[i - 1] == candidates[i] && used[i - 1] == false) {continue;
}
按“层”去重。只有当前层的数字和前一个数字相同时,才需要检查是否跳过。
3. 递归与回溯:
- 递归:将当前数字加入路径后,继续递归处理下一层。
- 回溯:撤销选择,包括移除路径中的数字,恢复 sum 和 used 的状态。
131.分割回文串
Java
class Solution {List<List<String>> result = new ArrayList<>();LinkedList<String> path = new LinkedList<>();public List<List<String>> partition(String s) {backtracking(s,0);return result;}public void backtracking(String s,int startIndex){if (startIndex >= s.length()){result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < s.length(); i++) {if (isPalindrome(s,startIndex,i)){String a = s.substring(startIndex,i+1);path.add(a);}else {continue;}backtracking(s,i+1);path.removeLast();}}boolean isPalindrome(String s,int start,int end){for (int i = start,j = end; i <j ; i++,j--) {if (s.charAt(i)!=s.charAt(j)){return false;}}return true;}
}
全局变量
List<List<String>> result = new ArrayList<>();
LinkedList<String> path = new LinkedList<>();
result:存储所有满足条件的分割方案。path:当前递归路径,表示当前的分割方案。
主函数
public List<List<String>> partition(String s) {backtracking(s, 0); // 从索引 0 开始划分字符串return result;
}
- 调用回溯函数
backtracking从字符串的第一个字符开始分割。 - 返回所有满足条件的方案。
回溯函数
public void backtracking(String s, int startIndex) {if (startIndex >= s.length()) {result.add(new ArrayList<>(path)); // 如果遍历到字符串末尾,记录当前路径return;}for (int i = startIndex; i < s.length(); i++) {if (isPalindrome(s, startIndex, i)) { // 判断从 startIndex 到 i 的子串是否是回文String a = s.substring(startIndex, i + 1); // 取出当前回文子串path.add(a); // 加入路径} else {continue; // 如果不是回文,跳过本次循环}backtracking(s, i + 1); // 递归处理剩下的部分path.removeLast(); // 回溯,移除最后一个子串}
}
- 终止条件:- 当
startIndex超过或等于字符串长度时,说明已经分割完毕,记录当前路径。 - 递归逻辑:- 从
startIndex开始,尝试分割到每个可能的位置i。- 如果
s[startIndex...i]是回文,则加入路径,并递归处理s[i+1...end]。 - 递归返回后,回溯移除当前子串。
- 如果
判断是否为回文
boolean isPalindrome(String s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s.charAt(i) != s.charAt(j)) {return false; // 如果两端字符不相等,不是回文}}return true; // 如果所有字符都相等,是回文
}
- 双指针法,检查从
start到end的子串是否为回文。 - 左右两端字符逐步比较,如果有任意一对不相等,则不是回文。
算法流程
- 从字符串
s的第一个字符开始,尝试划分每个可能的回文子串。 - 如果找到一个回文子串,加入当前路径,并继续递归处理剩余部分。
- 当划分到字符串末尾时,将当前路径记录为一种有效方案。
- 回溯时移除最后一个子串,尝试其他划分方式。
相关文章:

代码随想录day23 | leetcode 39.组合总和 40.组合总和II 131.分割回文串
39.组合总和 Java class Solution { List<List<Integer>> result new ArrayList<>();LinkedList<Integer> path new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sor…...
备考实战之分支结构(switch语句))
全国青少年信息学奥林匹克竞赛(信奥赛)备考实战之分支结构(switch语句)
if语句处理多个分支时需要用if-else if结构,分支越多,嵌套的if语句层就越多,程序不但庞大、复杂,理解起来也比较困难。在C编程中,针对有些问题除了使用if-else if结构之外,还有switch语句也可以实现&#x…...

R机器学习:决策树算法的理解与实操
今天继续给大家介绍决策树算法,决策树本身是一种非常简单直观的机器学习算法,用于做分类或回归任务。它就像我们平常做决定时的过程,通过逐步排除可能的选项,最终得出结论。 A decision tree is a flowchart-like structure used …...

解锁高效学习之道:从认知升级到实践突破
目录 学习之困:探寻低效的根源 (一)迷茫之境:目标缺失的困扰 (二)表象之迷:浅尝辄止的学习 (三)行动之阻:执行力的短板 认知重塑:明晰学习的本…...

2024年12月CCF-GESP编程能力等级认证Python编程三级真题解析
本文收录于专栏《Python等级认证CCF-GESP真题解析》,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 一、单选题(每题 2 分,共 30 分) 第 1 题 2024年10月8日,诺贝尔物理学奖“意外地”颁给了两位计算机科学家约翰霍普菲尔德(John J. Hopfield)和杰弗里辛顿(Geof…...

.NET Core 中使用 C# 获取Windows 和 Linux 环境兼容路径合并
在 .NET Core 中使用 C# 处理路径合并并确保在 Windows 和 Linux 环境中都能正常工作,可以使用 System.IO.Path 和 System.IO.Path.Combine 方法。它们是跨平台的,能够根据操作系统自动处理路径分隔符。可以通过 System.Runtime.InteropServices.Runtime…...
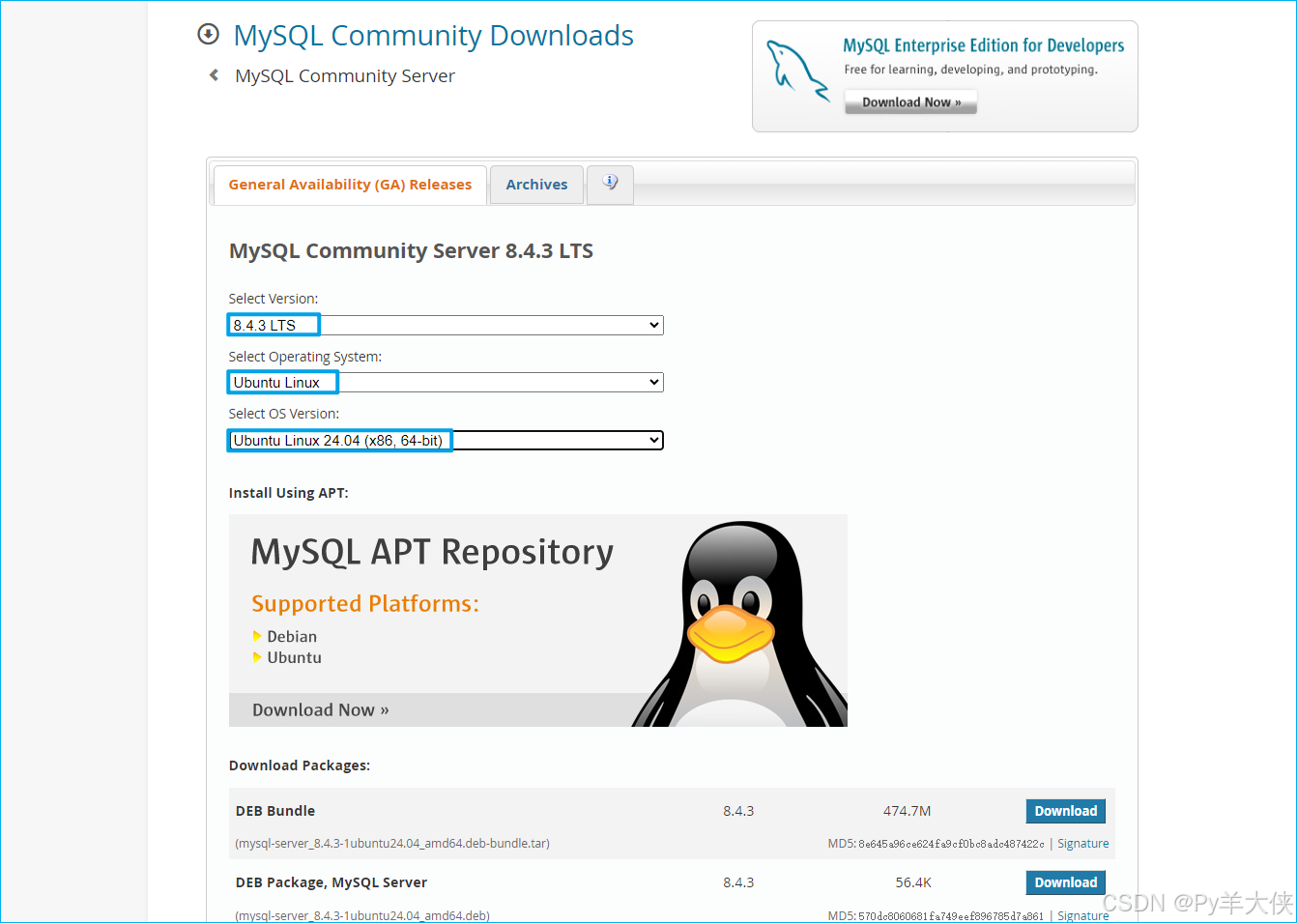
【SH】Ubuntu Server 24服务器搭建MySQL数据库研发笔记
文章目录 搭建服务器在线安装1. 更新软件包列表2. 安装MySQL3. 检查MySQL状态4. 修改密码5. 新增用户6. 设置局域网访问 离线安装下载安装包 常用命令参考文档在线安装日志 搭建服务器 作者羊大侠搭建的是 Ubuntu Server 24.04 LTS 服务器环境 搭建参考文档:【SH】…...
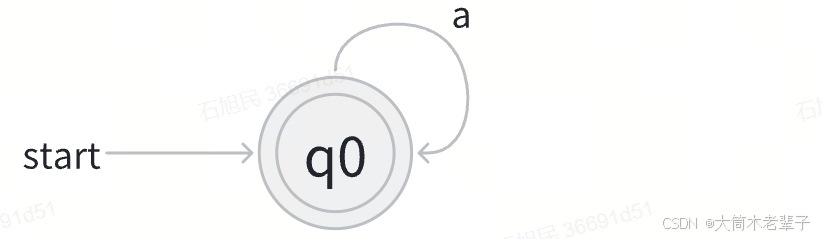
编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。 1. 正则表达式 正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式…...
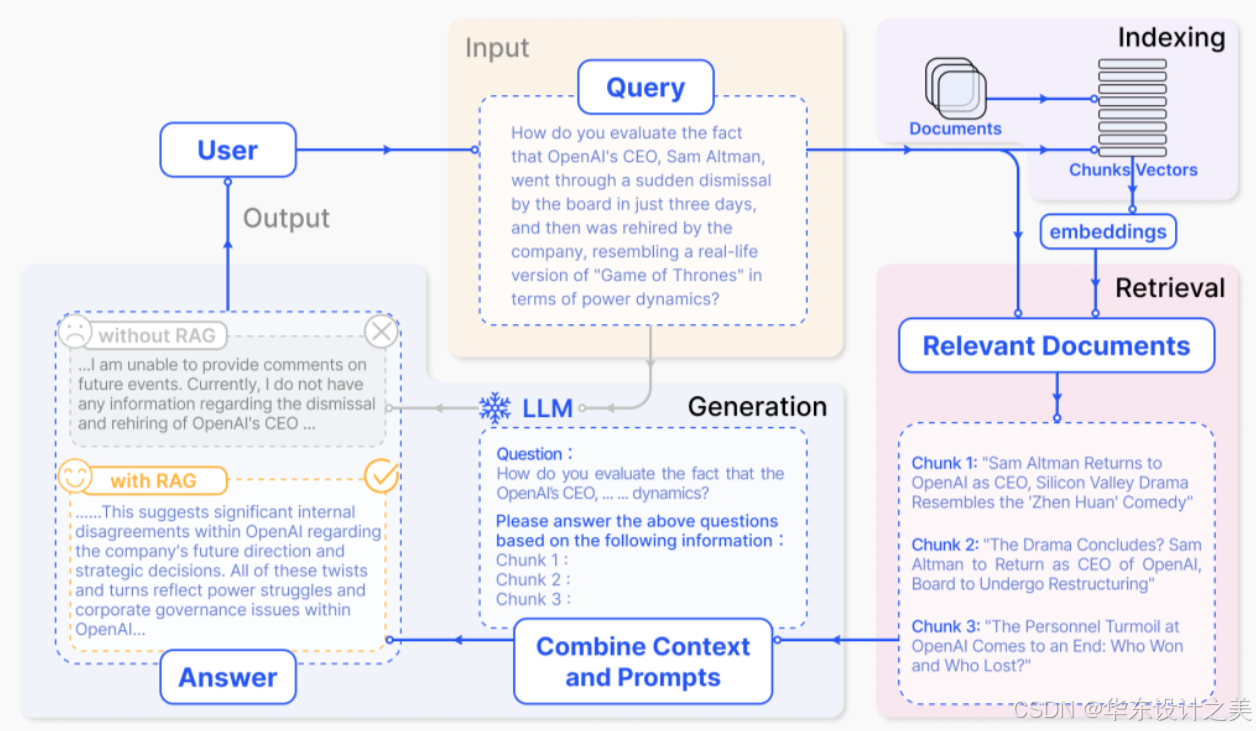
知识图谱+RAG学习
GraphRAG(Graph-based Retrieval-Augmented Generation)是微软在2024年推出的一项开源技术,旨在通过结合知识图谱和检索增强生成(RAG)方法,为大型语言模型(LLM)的数据处理提供全新解…...
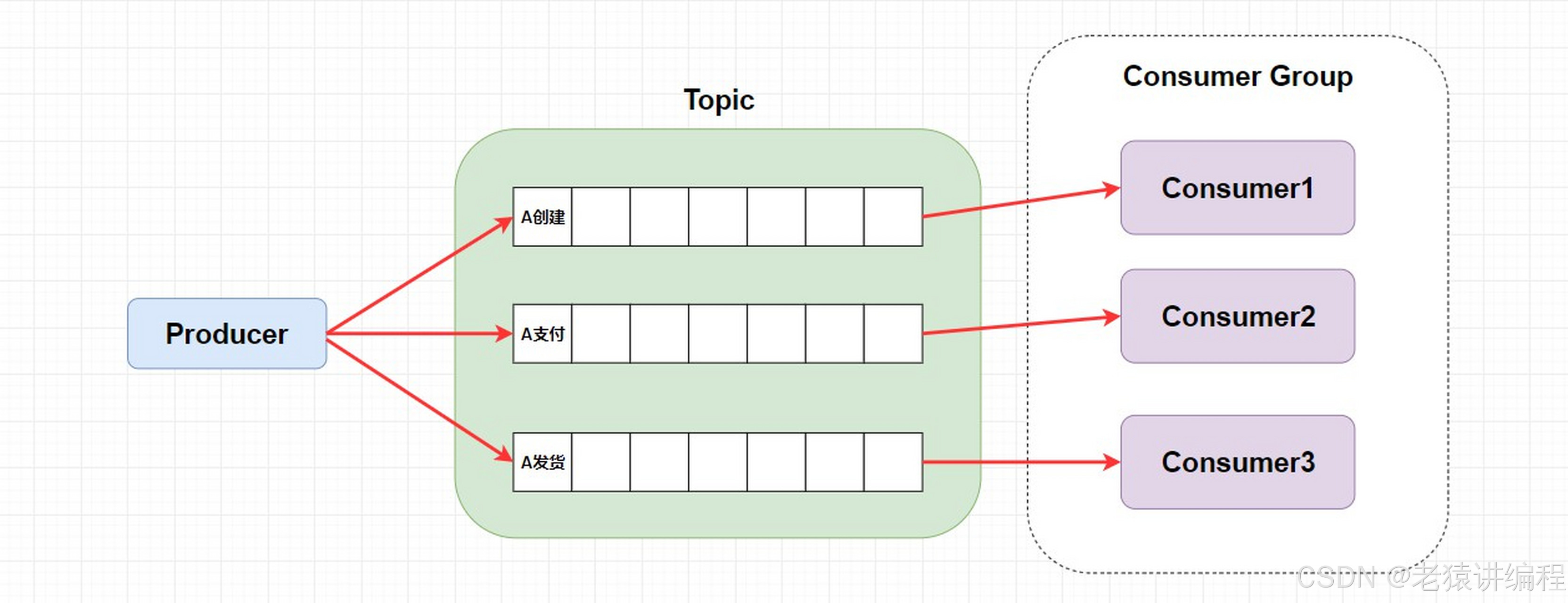
消息队列技术的发展历史
消息队列技术的演进历程宛如一幅波澜壮阔的科技画卷,历经多个标志性阶段,各阶段紧密贴合不同的技术需求与市场风向,下面为您详细道来。 第一阶段:消息中间件的起源(1970 年代末期 - 1980 年代中期) 在计算…...

每天40分玩转Django:Django部署
Django部署 一、今日学习内容概述 学习模块重要程度主要内容生产环境配置⭐⭐⭐⭐⭐settings配置、环境变量WSGI服务器⭐⭐⭐⭐⭐Gunicorn配置、性能优化Nginx配置⭐⭐⭐⭐反向代理、静态文件安全设置⭐⭐⭐⭐⭐SSL证书、安全选项 二、生产环境配置 2.1 项目结构调整 mypr…...
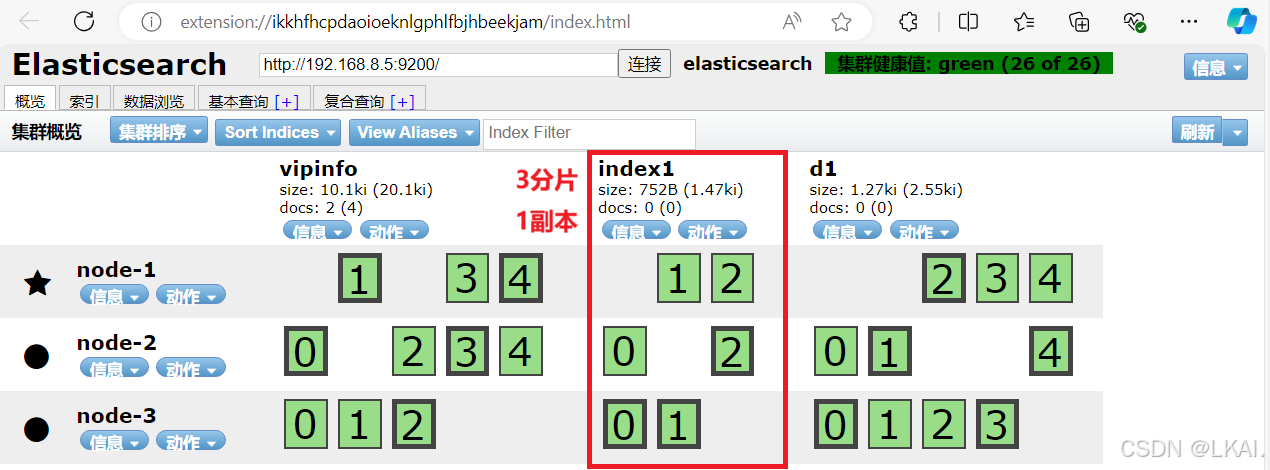
搭建Elastic search群集
一、实验环境 二、实验步骤 Elasticsearch 是一个分布式、高扩展、高实时的搜索与数据分析引擎Elasticsearch目录文件: /etc/elasticsearch/elasticsearch.yml#配置文件 /etc/elasticsearch/jvm.options#java虚拟机 /etc/init.d/elasticsearch#服务启动脚本 /e…...
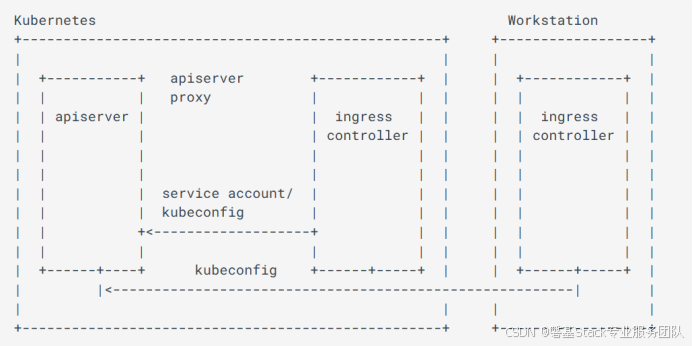
解析 Ingress-Nginx 故障:排查思路与方法
文章目录 一、什么是Ingress-Nginx二、故障排除1.1Ingress-Controller日志和事件检查 Ingress 资源事件检查 Nginx 配置检查使用的服务是否存在调试日志 1.2对 Kubernetes API 服务器的认证服务认证服务账户Kube-Config 1.3使用GDB和Nginx1.4在 Nginx 4.2.5 或其他版本…...

2024 楚慧杯 re wp
go_bytes 附件拖入ida 输入长度为0x28,每两位字符的4bit拼接 与一个常量值经过运算后的值进行异或,并且判断是否相等 脚本 bouquet 附件拖入ida。简单去一下花 构建了一个二叉树,然后递归调用函数 重新排列一下再层序遍历读出即可 zistel 附件…...

【物联网技术与应用】实验10:蜂鸣器实验
实验10 蜂鸣器实验 【实验介绍】 蜂鸣器是音频信号装置。蜂鸣器可分为有源蜂鸣器和无源蜂鸣器。 【实验组件】 ● Arduino Uno主板* 1 ● USB数据线* 1 ● 有源蜂鸣器* 1 ● 无源蜂鸣器* 1 ● 面包板* 1 ● 9V方型电池* 1 ● 跳线若干 【实验原理】 如图所示&#x…...
)
单片机:实现矩阵键盘控制LCD屏幕(附带源码)
单片机实现矩阵键盘控制LCD屏幕 矩阵键盘(Matrix Keypad)是一种常用的输入设备,广泛应用于嵌入式系统中。在许多嵌入式应用中,我们常常需要通过按键输入来控制系统的功能。结合LCD显示屏,我们可以实现一个简单的界面&…...

鸿蒙Next之包体积极限优化
鸿蒙应用包大小优化全解析 在鸿蒙应用开发中,减小应用包大小对于提升应用下载和安装体验起着关键作用。通过压缩、精简或复用应用中的代码与资源,能有效降低包体积,减少空间占用并加快下载与安装速度。下面详细介绍一下鸿蒙应用包大小优化的…...

Android实战经验篇-log工具
详细代码实现及系列文章请转如下链接 Android实战经验篇-系列文章汇总 Android Display Graphics系列文章-汇总 一、基础知识 1.1 Logging简述 我们写的第一个计算机C程序一般是printf(“Hello world!”);这就是一个log输出。Linux内核有Kernel log以及配套的Log工具&#x…...

DPU编程技术解析与实践应用
一、引言 1.1 研究背景与目的 随着信息技术的飞速发展,数据中心在现代社会中的地位日益凸显,成为支撑各行业数字化转型的关键基础设施。在数据中心内部,数据的处理速度、效率和安全性成为了影响整体性能的核心要素。为了应对不断增长的数据…...
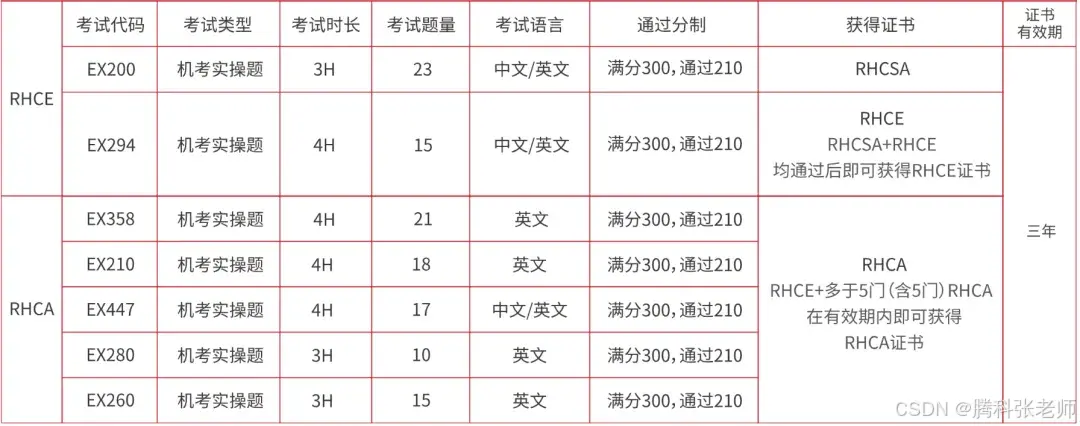
红帽认证的含金量和价值如何?怎么报名红帽认证考试?
红帽企业 Linux(RHEL)是由红帽公司提供的一款商业支持、专为生产环境设计的Linux发行版。随着IT系统和工作负载日益复杂化,底层基础设施及操作系统必须兼具可靠性、可扩展性,并能有效促进性能提升。红帽认证在全球范围享有盛誉&am…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
