2024-12-29-sklearn学习(25)无监督学习-神经网络模型(无监督) 烟笼寒水月笼沙,夜泊秦淮近酒家。
文章目录
- sklearn学习(25) 无监督学习-神经网络模型(无监督)
- 25.1 限制波尔兹曼机
- 25.1.1 图形模型和参数化
- 25.1.2 伯努利限制玻尔兹曼机
- 25.1.3 随机最大似然学习
sklearn学习(25) 无监督学习-神经网络模型(无监督)
文章参考网站:
https://sklearn.apachecn.org/
和
https://scikit-learn.org/stable/
25.1 限制波尔兹曼机
限制玻尔兹曼机(Restricted Boltzmann machines,简称 RBM)是基于概率模型的无监督非线性特征学习器。当用 RBM 或多层次结构的RBMs 提取的特征在馈入线性分类器(如线性支持向量机或感知机)时通常会获得良好的结果。
该模型对输入的分布作出假设。目前,scikit-learn 只提供了 BernoulliRBM,它假定输入是二值(binary values)的,或者是 0 到 1 之间的值,每个值都编码特定特征被激活的概率。
RBM 尝试使用特定图形模型最大化数据的似然。它所使用的参数学习算法(随机最大似然)可以防止特征表示偏离输入数据。这使得它能捕获到有趣的特征,但使得该模型对于小数据集和密度估计不太有效。
该方法在初始化具有独立 RBM 权值的深度神经网络时得到了广泛的应用。这种方法是无监督的预训练。

示例:
- Restricted Boltzmann Machine features for digit classification
25.1.1 图形模型和参数化
RBM 的图形模型是一个全连接的二分图。

节点是随机变量,其状态取决于它连接到的其他节点的状态。这个模型可通过连接的权重、以及每个可见或隐藏单元的偏置项进行参数化,为了简单起见,我们省略了上图中的偏置项。
用能量函数衡量联合概率分布的质量:
E ( v , h ) = − ∑ i ∑ j w i j v i h j − ∑ i b i v i − ∑ j c j h j E(\mathbf{v}, \mathbf{h}) = -\sum_i \sum_j w_{ij}v_ih_j - \sum_i b_iv_i - \sum_j c_jh_j E(v,h)=−i∑j∑wijvihj−i∑bivi−j∑cjhj
在上面的公式中, b \mathbf{b} b 和 c \mathbf{c} c 分别是可见层和隐藏层的偏置向量。模型的联合概率是根据能量来定义的:
P ( v , h ) = e − E ( v , h ) Z P(\mathbf{v}, \mathbf{h}) = \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z} P(v,h)=Ze−E(v,h)
“限制”是指模型的二分图结构,它禁止隐藏单元之间或可见单元之间的直接交互。 这代表以下条件独立性成立:
h i ⊥ h j ∣ v v i ⊥ v j ∣ h h_i \bot h_j | \mathbf{v} \\ v_i \bot v_j | \mathbf{h} hi⊥hj∣vvi⊥vj∣h
二分图结构允许使用高效的块吉比斯采样(block Gibbs sampling)进行推断。
25.1.2 伯努利限制玻尔兹曼机
在 BernoulliRBM 中,所有单位都是二进制随机单元。这意味着输入数据应该是二值,或者是在 0 和 1 之间的实数值,其表示可见单元活跃或不活跃的概率。 这是一个很好的字符识别模型,其中的关注点是哪些像素是活跃的,哪些不是。 对于自然场景的图像,它因为背景、深度和相邻像素趋势取相同的值而不再适合。
每个单位的条件概率分布由其接收的输入的 logistic sigmoid函数给出:
P ( v i = 1 ∣ h ) = σ ( ∑ j w i j h j + b i ) P ( h i = 1 ∣ v ) = σ ( ∑ i w i j v i + c j ) P(v_i=1|\mathbf{h}) = \sigma(\sum_j w_{ij}h_j + b_i) \\P(h_i=1|\mathbf{v}) = \sigma(\sum_i w_{ij}v_i + c_j) P(vi=1∣h)=σ(j∑wijhj+bi)P(hi=1∣v)=σ(i∑wijvi+cj)
其中 σ \sigma σ 是 logistic sigmoid函数:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
25.1.3 随机最大似然学习
在 BernoulliRBM 函数中实现的训练算法被称为随机最大似然(SML)或持续对比发散(PCD)。由于数据的似然函数的形式,直接优化最大似然是不可行的:
log P ( v ) = log ∑ h e − E ( v , h ) − log ∑ x , y e − E ( x , y ) \log P(v) = \log \sum_h e^{-E(v, h)} - \log \sum_{x, y} e^{-E(x, y)} logP(v)=logh∑e−E(v,h)−logx,y∑e−E(x,y)
为了简单起见,上面的等式是针对单个训练样本所写的。相对于权重的梯度由对应于上述的两个项构成。根据它们的符号,它们通常被称为正梯度和负梯度。这种实现按照小批量样本对梯度进行计算。
在最大化对数似然度(maximizing the log-likelihood)的情况下,正梯度使模型更倾向于与观察到的训练数据兼容的隐藏状态。RBM 的二分体结构使他可以被高效地计算。然而,负梯度是棘手的。其目标是降低模型偏好的联合状态的能量,从而使数据保持真实。它可以使用块吉比斯采样通过马尔可夫链蒙特卡罗来粗略估计,它通过迭代地对每个 v v v 和 h h h 进行交互采样,直到链混合。以这种方式产生的样本有时被称为幻想粒子。这是低效的,并且我们很难确定马可夫链是否混合。
对比发散方法建议在经过少量迭代后停止链,迭代数 k k k 通常为 1。该方法快速且方差小,但样本远离模型分布。
持续对比发散解决了这个问题。在 PCD 中,我们保留了多个链(幻想粒子)来在每个权重更新之后更新 k k k 个吉比斯采样步骤,而不是每次需要梯度时都启动一个新的链,并且只执行一个吉比斯采样步骤。这使得粒子能更彻底地探索空间。
参考资料:
“A fast learning algorithm for deep belief nets” G. Hinton, S. Osindero, Y.-W. Teh, 2006
“Training Restricted Boltzmann Machines using Approximations to the Likelihood Gradient” T. Tieleman, 2008
相关文章:

2024-12-29-sklearn学习(25)无监督学习-神经网络模型(无监督) 烟笼寒水月笼沙,夜泊秦淮近酒家。
文章目录 sklearn学习(25) 无监督学习-神经网络模型(无监督)25.1 限制波尔兹曼机25.1.1 图形模型和参数化25.1.2 伯努利限制玻尔兹曼机25.1.3 随机最大似然学习 sklearn学习(25) 无监督学习-神经网络模型(无监督) 文章参考网站&a…...

RSA e与phi不互质(AMM算法进行有限域开根)
e与phi不互质 这一部分学习来自trup师傅的博客 针对CTFer的e与phi不互素的问题 - 跳跳糖 1:m^t<n from Crypto.Util.number import * from secret import flag flag bflag{*********} m bytes_to_long(flag) p getPrime(1024) q getPrime(1024) n p * q …...

网络物理互连
案例简介 美乐公司为新创建公司,公司现需要架设网络,需要下属分公司通过路由器与外网服务器联通,请使用Packet Tracer, 按照任务要求完成实验。实验中需配置设备或端口的IP地址。 1、绘制拓扑图 2、配置ip地址 3、配置路由ip R0 …...

论文研读:Text2Video-Zero 无需微调,仅改动<文生图模型>推理函数实现文生视频(Arxiv 2023-03-23)
论文名:Text2Video-Zero: Text-to-Image Diffusion Models are Zero-Shot Video Generators 1. 摘要 1.1 方法总结 通过潜空间插值, 实现动作连续帧。 以第一帧为锚定,替换原模型的self-attention,改为cross-attention 实现 保证图片整体场…...

服务端错误的处理和web安全检测
文章目录 I 服务端错误的处理业务返回码处理前端处理业务返回码nginx处理http状态码II web安全检测区分服务器类型主机扫漏III 使用 micro_httpd 搭建一个PHP站点步骤下载micro_httpd 并安装它配置micro_httpd 来服务PHP文件I 服务端错误的处理 服务端发生错误时,返回给前端的…...
鸿蒙TCPSocket通信模拟智能家居模拟案例
效果图 一、智能家居热潮下的鸿蒙契机 在当下科技飞速发展的时代,智能家居已如浪潮般席卷而来,深刻地改变着我们的生活方式。从能依据环境光线自动调节亮度的智能灯具,到可远程操控、精准控温的智能空调,再到实时监测健康数据的智…...

SQL-leetcode-197. 上升的温度
197. 上升的温度 表: Weather ---------------------- | Column Name | Type | ---------------------- | id | int | | recordDate | date | | temperature | int | ---------------------- id 是该表具有唯一值的列。 没有具有相同 recordDate 的不同行。 该表包…...

C++系列关键字static
文章目录 1.静态变量2.静态成员变量 1.静态变量 在C的,静态变量是一个非常有用的特性,它在程序执行期间只初始化一次,并在程序的整个执行期间都保持其值。 1.局部静态变量。定义在函数中,只初始化一次,不像普通的局部…...

使用Fn Connect之后,如何访问到其他程序页面?原来一直都可以!
前言 昨天小白讲过在飞牛上登录Fn Connect,就可以实现远程访问家里的NAS。 接着就有小伙伴咨询:如何远程访问到家里其他需要使用不同端口号才能访问到的软件,比如Jellyfin、Emby等。 这个小白在写文章的时候确实没有考虑到,因为…...

探索Composable Architecture:小众但高效的现代框架技术
近年来,随着应用规模和复杂性的不断提升,对开发效率和可维护性的要求也水涨船高。特别是在领域驱动设计 (DDD) 和反应式编程 (Reactive Programming) 的趋势影响下,一些小众但极具潜力的框架应运而生。本篇博客将深入探讨一种日益受到关注但尚…...

改投论文时如何重构
摘要: 不同期刊和会议对于论文的风格、页数限制等方面有一些差别, 论文在某个地方被拒, 改投别处时需要进行重构. 本贴描述重构的基本方案. 你的衣柜乱糟糟的, 如何清理呢? 方案 A. 把不喜欢的衣服一件件丢掉.方案 B. 把衣服全部丢出来, 然后再把喜欢的衣服一件件放进去. 对…...

P8打卡——YOLOv5-C3模块实现天气识别
🍨 本文为🔗365天深度学习训练营中的学习记录博客🍖 原作者:K同学啊 1.检查GPU import torch import torch.nn as nn import torchvision.transforms as transforms import torchvision from torchvision import transforms, dat…...

基于微信小程序的校园点餐平台的设计与实现(源码+SQL+LW+部署讲解)
文章目录 摘 要1. 第1章 选题背景及研究意义1.1 选题背景1.2 研究意义1.3 论文结构安排 2. 第2章 相关开发技术2.1 前端技术2.2 后端技术2.3 数据库技术 3. 第3章 可行性及需求分析3.1 可行性分析3.2 系统需求分析 4. 第4章 系统概要设计4.1 系统功能模块设计4.2 数据库设计 5.…...

PyTorch快速入门教程【小土堆】之完整模型训练套路
视频地址完整的模型训练套路(一)_哔哩哔哩_bilibili import torch import torchvision from model import * from torch import nn from torch.utils.data import DataLoader# 准备数据集 train_data torchvision.datasets.CIFAR10(root"CIFAR10&…...

【AIGC】 ChatGPT实战教程:如何高效撰写学术论文引言
💥 欢迎来到我的博客!很高兴能在这里与您相遇! 首页:GPT-千鑫 – 热爱AI、热爱Python的天选打工人,活到老学到老!!!导航 - 人工智能系列:包含 OpenAI API Key教程, 50个…...

TTL 传输中过期问题定位
问题: 工作环境中有一个acap的环境,ac的wan口ip是192.168.186.195/24,ac上lan上有vlan205,其ip子接口地址192.168.205.1/24,ac采用非nat模式,而是路由模式,在上级路由器上有192.168.205.0/24指向…...

非docker方式部署openwebui过程记录
之前一直用docker方式部署openwebui,结果这东西三天两头升级,我这一升级拉取docker镜像硬盘空间嗖嗖的占用,受不了,今天改成了直接部署,以下是部署过程记录。 一、停止及删除没用的docker镜像占用的硬盘空间 docker s…...

大模型的prompt的应用二
下面总结一些在工作中比较实用的prompt应用。还可以到以下网站参考更多的prompt AI Prompts - WayToAGI 举个例子,让大模型写一份周报 # 角色:智能周报编写助手 ## 背景: 需要根据产品经理提供的简要周报框架,补充完整的周报内容。 ## 注意事项: 言简意赅,重点突…...

ubuntu 22.04安装ollama
1. 顺利的情况 按照官网的提示,执行下面的命令: curl -fsSL https://ollama.com/install.sh | sh如果网络畅通,github访问也没有问题,那就等待安装完成就行 2. 不顺利的情况 由于众所周知的情况,国内网络访问githu…...
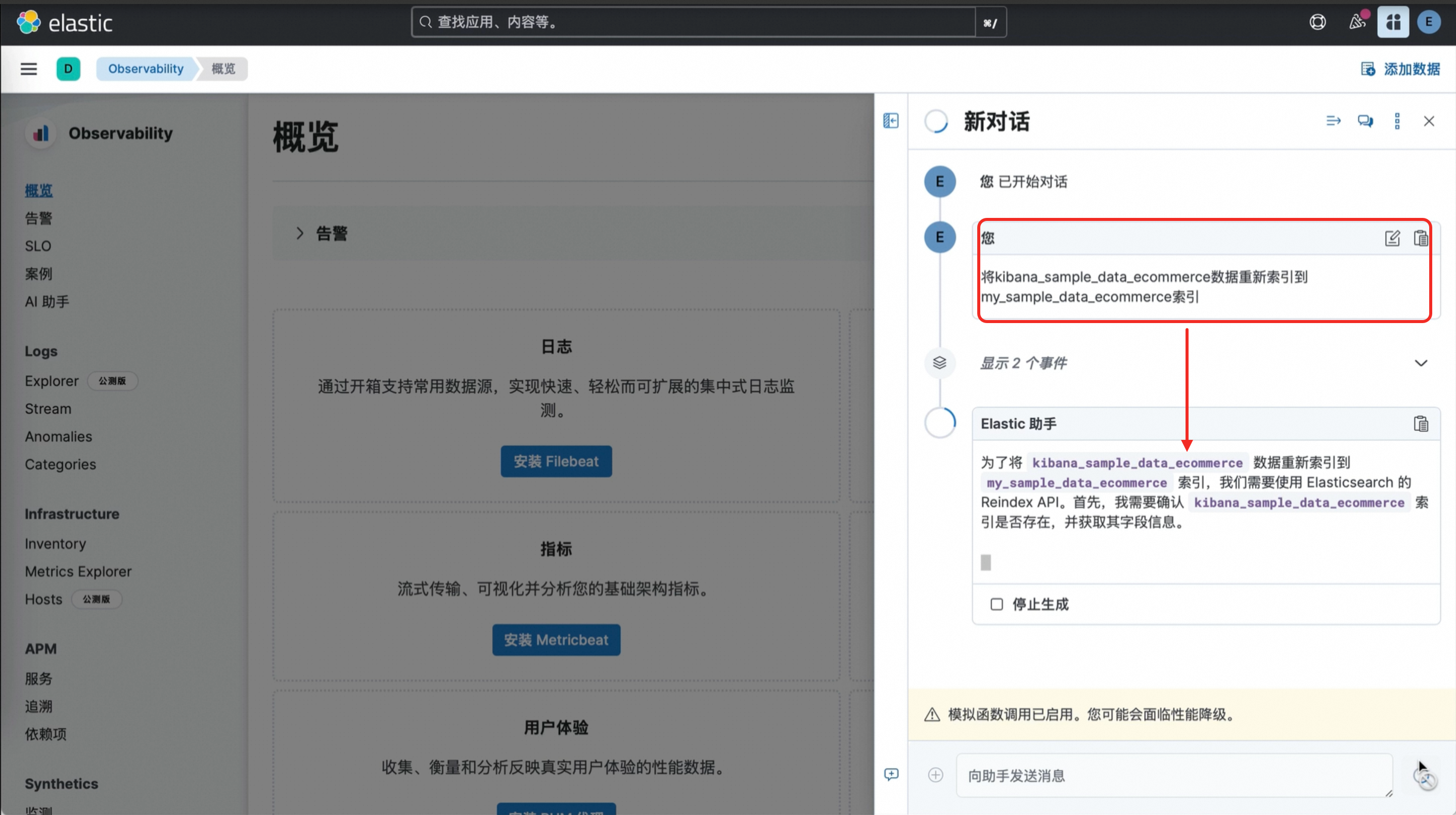
从企业级 RAG 到 AI Assistant,阿里云 Elasticsearch AI 搜索技术实践
在过去一年中,基座大模型技术的快速迭代推动了 AI 搜索的演进,主要体现在以下几个方面: 1.搜索技术链路重构 基于大模型的全面重构正在重塑 AI 搜索的技术链路。从数据采集、文档解析、向量检索到查询分析、意图识别、排序模型和知识图谱等…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
