当前位置： 首页 > news >正文

统计学习方法（第二版） 概率分布学习

news 2025/12/30 1:21:05

本文主要介绍机器学习的概率分布，帮助后续的理解。

定义直接从书上搬的想自己写，但没有定义准确，还浪费事件，作为个人笔记，遇到速查。

目录

一、二点分布（0-1分布、伯努利分布）

二、二项分布（离散分布）

三、泊松分布（离散分布）

四、范畴分布（离散分布）

五、均匀分布（连续分布）

五、正态分布、高斯分布、标准正态分布（连续分布）

六、指数分布（连续分布）

七、拉普拉斯分布（Laplace）（连续分布）

总结

一、二点分布（0-1分布、伯努利分布）

E(X) = p

Var(X) = p(1-p)

二、二项分布（离散分布）

E(X) = np

Var(X) = np(1-p)

三、泊松分布（离散分布）

E(X) = \lambda

Var(X) = \lambda

四、范畴分布（离散分布）

在这里举个例子吧！

比如说掷骰子结果有6中状态，也就是k = 6，可以知道6种情况的概率为1，所以当我们已知5种情况的概率，就能计算出剩一种情况的概率。这就是范畴分布。

五、均匀分布（连续分布）

五、正态分布、高斯分布、标准正态分布（连续分布）

六、指数分布（连续分布）

七、拉普拉斯分布（Laplace）（连续分布）

在概率论和统计学中，拉普拉斯是一种连续概率分布。由于它可以看做是俩个不同位置的指数分布背靠背拼在一起，所以它也叫做双指数分布。如果随机变量的概率密度函数分布为：

f(x \mid u, b)=\frac{1}{2 b} \exp \left(-\frac{|x-u|}{b}\right)=\frac{1}{2 b}\left\{\begin{array}{l} \exp \left(-\frac{x-u}{b}\right), \text { if } x \geq u \\ \exp \left(-\frac{x-x}{b}\right), \text { if } x<u \end{array}\right.

​

​

​

总结

简单介绍几个概率分布，这太多太难了，无语死！

相关文章：

统计学习方法（第二版） 概率分布学习

本文主要介绍机器学习的概率分布&#xff0c;帮助后续的理解。 定义直接从书上搬的想自己写&#xff0c;但没有定义准确&#xff0c;还浪费事件&#xff0c;作为个人笔记&#xff0c;遇到速查。 目录 一、二点分布&#xff08;0-1分布、伯努利分布&#xff09; 二、二项分布…...

编程日记 2025/1/11 3:26:03

淺談Cocos2djs逆向

前言 簡單聊一下cocos2djs手遊的逆向&#xff0c;有任何相關想法歡迎和我討論^^ 一些概念 列出一些個人認為比較有用的概念&#xff1a; Cocos遊戲的兩大開發工具分別是CocosCreator和CocosStudio&#xff0c;區別是前者是cocos2djs專用的開發工具&#xff0c;後者則是coco…...

编程日记 2025/1/11 3:20:59

【ROS2】RViz2加载URDF模型文件

1、RViz2加载URDF模型文件 1）运行RViz2 rviz22）添加组件：RobotModel 3）选择通过文件添加 4）选择URDF文件，此时会报错，需要修改Fixed Frame为map即可 5）因为没有坐标转换，依然会报错，下面尝试解决 2、运行坐标转换节点 1）运行ROS节点：robot_state_publishe...

编程日记 2025/1/11 3:16:56

Unity导入特效，混合模式无效问题

检查spine导出设置与Unity导入设置是否一致 检查Blend Mode Materials是否勾选 检查是否使用导入时产生的对应混合模式的材质&#xff0c;混合模式不适用默认材质 这里选导入时生成的材质...

编程日记 2025/1/11 3:12:52

el-table自定义按钮控制扩展expand

需求&#xff1a;自定义按钮实现表格扩展内容的展开和收起&#xff0c;实现如下&#xff1a; 将type“expand”的表格列的宽度设置为width"1"&#xff0c;让该操作列不展示出来&#xff0c;然后通过ref动态调用组件的内部方法toggleRowExpansion(row, row.expanded)控…...

编程日记 2025/1/11 3:11:51

opencv CV_TM_SQDIFF未定义标识符

opencv CV_TM_SQDIFF未定义标识符 opencv4部分命名发生变换&#xff0c;将CV_WINDOW_AUTOSIZE改为WINDOW_AUTOSIZE&#xff1b;CV_TM_SQDIFF_NORMED改为TM_SQDIFF_NORMED。...

编程日记 2025/1/11 3:09:50

2024acl论文体悟

总结分析归纳 模型架构与训练方法&#xff1a;一些论文关注于改进大语言模型的架构和训练方法&#xff0c;以提高其性能和效率。例如&#xff0c;“Quantized Side Tuning: Fast and Memory-Efficient Tuning of Quantized Large Language Models”提出了一种量化侧调优方法&a…...

编程日记 2025/1/11 3:04:45

【Git原理与使用】版本回退reset 详细介绍、撤销修改、删除文件

目录 一、版本回退 reset 1.1 指令&#xff1a; 1.2 参数说明&#xff1a; 1.3 演示&#xff1a; 二、撤销修改 情况一&#xff1a;对于工作区的代码&#xff0c;还没有 add 情况二&#xff1a;已经 add &#xff0c;但没有 commit 情况三&#xff1a;已经 add &…...

编程日记 2025/1/11 3:03:43

反规范化带来的数据不一致问题的解决方案

在数据库设计中&#xff0c;规范化&#xff08;Normalization&#xff09;和反规范化&#xff08;Denormalization&#xff09;是两个相互对立但又不可或缺的概念。规范化旨在消除数据冗余&#xff0c;确保数据的一致性和准确性&#xff0c;但可能会降低查询效率。相反&#xf…...

编程日记 2025/1/11 3:02:41

【Android】直接使用binder的transact来代替aidl接口

aidl提供了binder调用的封装&#xff0c;有的时候&#xff0c;比如&#xff1a; 1. 懒得使用aidl生成的接口文件&#xff08;确实是懒&#xff0c;Android studio中aidl生成接口文件很方便&#xff09; 2. 服务端的提供者只公开了部分接口出来&#xff0c;只给了调用编号和参…...

编程日记 2025/1/11 2:59:37

Python机器学习笔记（十八、交互特征与多项式特征）

添加原始数据的交互特征&#xff08;interaction feature&#xff09;和多项式特征&#xff08;polynomial feature&#xff09;可以丰富特征表示&#xff0c;特别是对于线性模型。这种特征工程可以用统计建模和许多实际的机器学习应用中。 上一次学习&#xff1a;线性模型对w…...

编程日记 2025/1/11 2:48:25

《跟我学Spring Boot开发》系列文章索引❤（2025.01.09更新）

章节文章名备注第1节Spring Boot&#xff08;1&#xff09;基于Eclipse搭建Spring Boot开发环境环境搭建第2节Spring Boot&#xff08;2&#xff09;解决Maven下载依赖缓慢的问题给火车头提提速第3节Spring Boot&#xff08;3&#xff09;教你手工搭建Spring Boot项目纯手工玩法…...

编程日记 2025/1/11 2:42:20

【AI进化论】 如何让AI帮我们写一个项目系列：将Mysql生成md文档

一、python脚本 下面给出一个简易 Python 脚本示例&#xff0c;演示如何自动获取所有表的结构&#xff0c;并生成一份 Markdown 文件。你可根据自己的需求做修改或使用其他编程语言。 import mysql.connector# ------------------------ # 1. 连接数据库 # -----------------…...

编程日记 2025/1/11 2:41:19

(已开源-AAAI25) RCTrans：雷达相机融合3D目标检测模型

在雷达相机融合三维目标检测中&#xff0c;雷达点云稀疏、噪声较大&#xff0c;在相机雷达融合过程中提出了很多挑战。为了解决这个问题&#xff0c;我们引入了一种新的基于query的检测方法 Radar-Camera Transformer (RCTrans)。具体来说&#xff1a; 首先设计了一个雷达稠密…...

编程日记 2025/1/11 2:40:18

Elasticsearch：在 HNSW 中提前终止以实现更快的近似 KNN 搜索

作者&#xff1a;来自 Elastic Tommaso Teofili 了解如何使用智能提前终止策略让 HNSW 加快 KNN 搜索速度。 在高维空间中高效地找到最近邻的挑战是向量搜索中最重要的挑战之一&#xff0c;特别是当数据集规模增长时。正如我们之前的博客文章中所讨论的&#xff0c;当数据集规模…...

编程日记 2025/1/11 2:37:13

unittest VS pytest

以下是 unittest 和 pytest 框架的对比表格&#xff1a; 特性unittestpytest设计理念基于类的设计&#xff0c;类似于 Java 的 JUnit更简洁&#xff0c;基于函数式编程设计&#xff0c;支持类和函数两种方式测试编写需要继承 unittest.TestCase 类&#xff0c;方法以 test_ 开…...

编程日记 2025/1/11 2:28:03

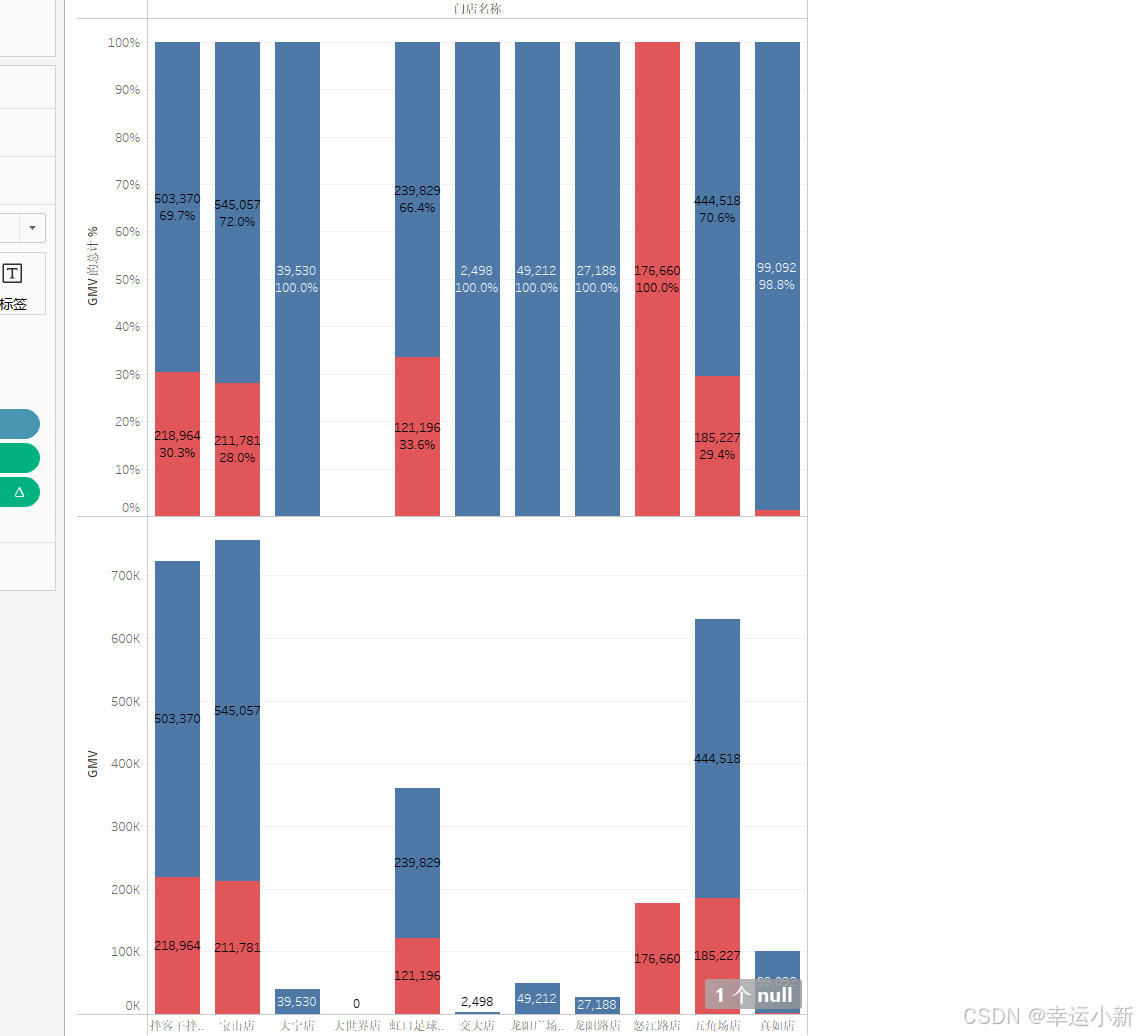
Tableau数据可视化与仪表盘搭建-基础图表制作

目录 对比分析&#xff1a;比大小 柱状图 条形图 数据钻取 筛选器 热力图 气泡图 变化分析&#xff1a;看趋势 折线图 预测 面积图 关系分布&#xff1a;看位置 散点图 直方图 地图 构成分析&#xff1a;看占比 饼图 树地图 堆积图 对比分析&#xff1a;比大…...

编程日记 2025/1/11 2:21:56

Center Loss 和 ArcFace Loss 笔记

一、Center Loss 1. 定义 Center Loss 旨在最小化类内特征的离散程度&#xff0c;通过约束样本特征与其类别中心之间的距离&#xff0c;提高类内特征的聚合性。 2. 公式 对于样本 xi​ 和其类别yi​&#xff0c;Center Loss 的公式为&#xff1a; xi​: 当前样本的特征向量&…...

编程日记 2025/1/11 2:17:52

3125: 【入门】求1/1+1/2+2/3+3/5+5/8+8/13+13/21……的前n项的和

文章目录 题目描述输入输出样例输入样例输出 题目描述 求1/11/22/33/55/88/1313/2121/34……的前n项的和。 输入 第1行&#xff1a;一个整数n&#xff08;1 < n < 30 &#xff09;。 输出 一行&#xff1a;一个小数&#xff0c;即前n项之和&#xff08;保留3位小数&…...

编程日记 2025/1/11 2:16:49

如何确保获取的淘宝详情页数据的准确性和时效性？

要确保获取的淘宝详情页数据的准确性和时效性&#xff0c;可从以下几个方面着手&#xff1a; 合法合规获取数据 遵守平台规则&#xff1a;在获取淘宝详情页数据之前&#xff0c;务必仔细阅读并严格遵守淘宝平台的使用协议和相关规定。明确哪些数据可以获取、以何种方式获取以及…...

编程日记 2025/1/11 2:09:41

基于大模型的 UI 自动化系统

基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

编程新知 2025/10/22 11:16:20

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2025/8/4 18:55:37

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

企业如何增强终端安全？

在数字化转型加速的今天&#xff0c;企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机&#xff0c;到工厂里的物联网设备、智能传感器&#xff0c;这些终端构成了企业与外部世界连接的 “神经末梢”。然而&#xff0c;随着远程办公的常态化和设备接入的爆炸式…...

编程新知 2025/12/9 13:14:46

作为测试我们应该关注redis哪些方面

1、功能测试 数据结构操作&#xff1a;验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化&#xff1a;测试aof和aof持久化机制&#xff0c;确保数据在开启后正确恢复。 事务&#xff1a;检查事务的原子性和回滚机制。 发布订阅&#xff1a;确保消息正确传递。 2、性…...

编程新知 2025/11/1 2:00:51

【SpringBoot自动化部署】

SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一&#xff0c;能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时&#xff0c;需要添加Git仓库地址和凭证&#xff0c;设置构建触发器&#xff08;如GitHub…...

编程新知 2025/11/18 2:17:20

沙箱虚拟化技术虚拟机容器之间的关系详解

问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西&#xff0c;但是如果把三者放在一起&#xff0c;它们之间到底什么关系&#xff1f;又有什么联系呢&#xff1f;我不是很明白&#xff01;&#xff01;&#xff01; 就比如说&#xff1a; 沙箱&#…...

编程新知 2025/12/24 23:40:36

DeepSeek越强，Kimi越慌？

被DeepSeek吊打的Kimi&#xff0c;还有多少人在用&#xff1f; 去年&#xff0c;月之暗面创始人杨植麟别提有多风光了。90后清华学霸&#xff0c;国产大模型六小虎之一&#xff0c;手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水&#xff0c;单月光是投流就花费2个亿。 疯…...

编程新知 2025/12/22 1:20:48

动态规划-1035.不相交的线-力扣(LeetCode)

一、题目解析 光看题目要求和例图&#xff0c;感觉这题好麻烦&#xff0c;直线不能相交啊&#xff0c;每个数字只属于一条连线啊等等&#xff0c;但我们结合题目所给的信息和例图的内容&#xff0c;这不就是最长公共子序列吗&#xff1f;&#xff0c;我们把最长公共子序列连线起…...

编程新知 2025/12/24 20:39:13