浮点数在C语言开发中为什么不精确?
在C语言开发中,浮点数的精度问题是一个常见的陷阱,尤其是对于刚接触编程的开发者来说,可能会对浮点数的行为感到困惑。为什么0.1 + 0.2不等于0.3?为什么浮点数计算会出现微小误差?本文将从计算机底层原理出发,深入探讨浮点数在C语言中不精确的原因,并给出一些实际开发中的应对策略。
1. 浮点数的表示方式
1.1 IEEE 754 标准
现代计算机通常使用 IEEE 754 标准 来表示浮点数。该标准将浮点数分为三个部分:
- 符号位(Sign):表示正负。
- 指数位(Exponent):表示浮点数的规模。
- 尾数位(Mantissa/Fraction):表示浮点数的精度。
例如,一个32位的单精度浮点数(float)的格式如下:
| 1位符号位 | 8位指数位 | 23位尾数位 |
1.2 浮点数的精度问题
浮点数的尾数位是有限的(单精度23位,双精度52位),这意味着它只能表示有限的二进制小数。许多十进制小数(如0.1)在二进制中是无限循环小数,无法精确表示,因此会被截断或舍入,导致精度丢失。
2. 为什么浮点数不精确?
2.1 二进制无法精确表示某些十进制小数
十进制中的0.1在二进制中是一个无限循环小数:
0.1 (十进制) = 0.0001100110011001100110011001100110011... (二进制)
由于浮点数的尾数位有限,计算机只能存储这个无限循环小数的前几位,因此0.1在计算机中并不是精确的。
2.2 浮点数运算的舍入误差
浮点数在进行加减乘除运算时,可能会引入舍入误差。例如:
#include <stdio.h>int main() {float a = 0.1;float b = 0.2;float c = a + b;printf("0.1 + 0.2 = %.20f\n", c); // 输出:0.30000001192092895508return 0;
}
由于0.1和0.2都无法精确表示,它们的和0.3也会存在微小误差。
2.3 浮点数的范围限制
浮点数的指数位决定了它能表示的范围。如果数值超出浮点数的表示范围,会导致溢出(Infinity)或下溢(0),进一步影响精度。
3. 浮点数精度问题的实际影响
3.1 比较浮点数
由于浮点数存在微小误差,直接比较两个浮点数是否相等是不可靠的。例如:
if (0.1 + 0.2 == 0.3) {printf("Equal\n");
} else {printf("Not equal\n"); // 实际输出
}
正确的做法是比较它们的差值是否小于一个极小的阈值(epsilon):
#include <math.h>if (fabs((0.1 + 0.2) - 0.3) < 1e-6) {printf("Equal\n"); // 正确输出
}
3.2 累积误差
在多次浮点数运算中,误差会逐渐累积,导致结果偏离预期。例如:
#include <stdio.h>int main() {float sum = 0.0;for (int i = 0; i < 1000; i++) {sum += 0.1;}printf("Sum: %.20f\n", sum); // 输出:100.00000149011611938477return 0;
}
可以看到,累加0.11000次后,结果并不是精确的100.0。
4. 如何应对浮点数精度问题?
4.1 使用高精度库
如果需要更高的精度,可以使用高精度数学库(如GMP或MPFR),它们支持任意精度的浮点数运算。
4.2 避免直接比较浮点数
使用差值比较法,判断两个浮点数的差值是否小于一个极小的阈值。
4.3 使用整数代替浮点数
在某些场景下,可以将浮点数转换为整数进行计算。例如,货币计算可以使用“分”而不是“元”作为单位。
4.4 减少运算次数
尽量减少浮点数的运算次数,避免误差累积。
5. 总结
浮点数在C语言中不精确的根本原因在于其二进制表示方式的局限性。IEEE 754 标准的浮点数只能近似表示某些十进制小数,并且在运算过程中会引入舍入误差。在实际开发中,我们需要理解浮点数的工作原理,并采取适当的策略来应对精度问题。
通过使用高精度库、避免直接比较浮点数、减少运算次数等方法,可以有效降低浮点数精度问题对程序的影响。希望本文能帮助你更好地理解浮点数在C语言中的行为,并在开发中避免常见的陷阱。
相关文章:

浮点数在C语言开发中为什么不精确?
在C语言开发中,浮点数的精度问题是一个常见的陷阱,尤其是对于刚接触编程的开发者来说,可能会对浮点数的行为感到困惑。为什么0.1 0.2不等于0.3?为什么浮点数计算会出现微小误差?本文将从计算机底层原理出发࿰…...

ChatGPT网络错误如何解决
在当今的信息化社会,网络技术已无处不在。无论是日常生活中的在线购物,还是工作中的远程会议,网络的稳定性和可靠性成为了我们无时无刻不在关注的重要问题。而在智能技术的快速发展中,像ChatGPT这样的人工智能模型,因其…...

Vue3初学之插槽(slot)使用
在 Vue 3 中,插槽(Slots)是一种强大的内容分发机制,允许你在组件中定义可替换的内容区域,从而使组件更加通用和灵活。以下是 Vue 3 中插槽的几种常见用法: 默认插槽 默认插槽是最基本的插槽类型࿰…...
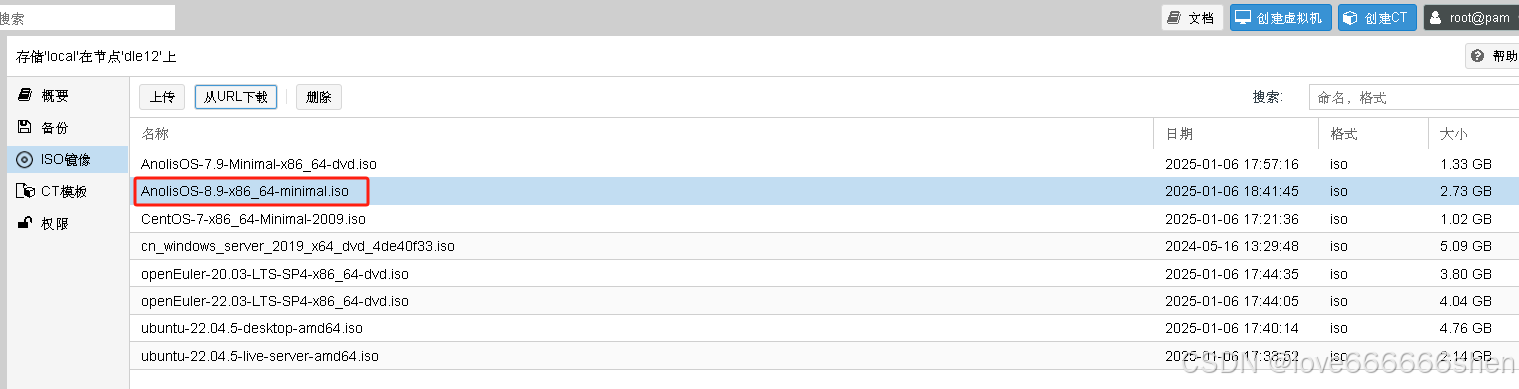
使用PVE快速创建虚拟机集群并搭建docker环境
安装Linux系统 这里以安装龙蜥操作系统AnolisOS8.9为例加以说明。 通过PVE后台上传操作系统ISO镜像。 然后在PVE上【创建虚拟机】,选定上传的龙蜥操作系统镜像进行系统安装。 注意:在安装过程中,要设定语言、时区、超管用户root的密码、普…...
带格式 pdf 翻译
支持 openAI 接口,国内 deepseek 接口兼容 openAI 接口, deepseek api 又非常便宜 https://pdf2zh.com/ https://github.com/Byaidu/PDFMathTranslate...
【C++】C++11(一)
目录 一、C11简介二、统一的列表初始化2.1 {}初始化2.2 std::initializer_list 三、声明3.1 auto3.2 decltype3.3 nullptr 四、范围for五、智能指针六、STL中一些变化七、右值引用和移动语义7.1 左值引用和右值引用7.2 左值引用与右值引用比较7.3 右值引…...
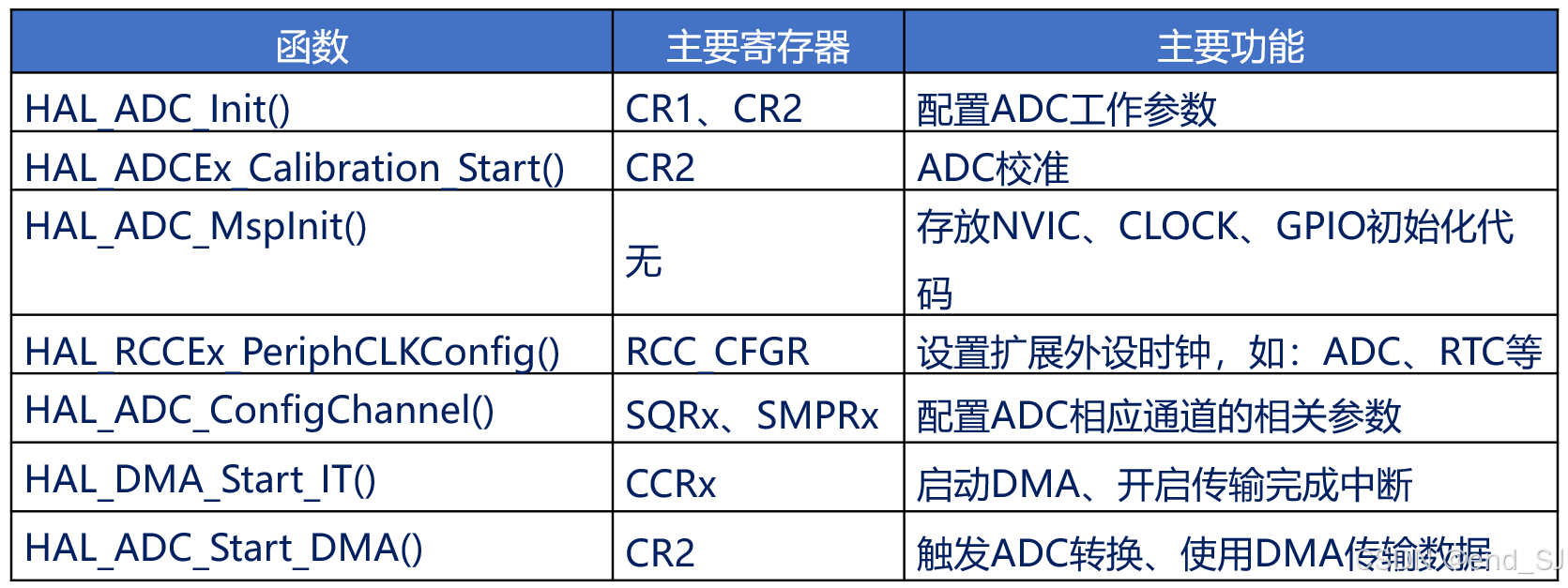
初学stm32 --- ADC单通道采集
目录 ADC寄存器介绍(F1) ADC控制寄存器 1(ADC_CR1) ADC控制寄存器 2(ADC_CR2) ADC采样时间寄存器1(ADC_SMPR1) ADC采样时间寄存器2(ADC_SMPR2) ADC规则序列寄存器 1(ADC_SQR1) ADC规则序列寄存器 2(ADC_SQR2) ADC规则序列寄存器 3(ADC_SQR3) AD…...

【动态规划篇】欣赏概率论与镜像法融合下,别出心裁探索解答括号序列问题
本篇鸡汤:没有人能替你承受痛苦,也没有人能拿走你的坚强. 欢迎拜访:羑悻的小杀马特.-CSDN博客 本篇主题:带你解答洛谷的括号序列问题(绝对巧解) 制作日期:2025.01.10 隶属专栏:C/C题…...
Java(day7)
字符串练习 生成验证码 package day6; /*生成验证码 内容:可以是小写字母,也可以是大写字,还可以是数字 规则: 长度为5 内容中是四位字母,1位数字。 其中数字只有1位,但是可以出现在任意的位置。*/ impor…...

Word 转成pdf及打印的开源方案支持xp
Word转成pdf、打印的方案几乎没有免费开源的方案,现在提供一个通过LibreOffice实现的方案 操作依赖LibreOffice需要安装,点此下载老版本 5.4.7.2是最后一个支持xp的 版本如需xp要请安装此版本 LibreOffice官方介绍 LibreOffice 是一款开放源代码的自…...

LabVIEW软件侵权分析与应对
问:如果涉及到LabVIEW软件的仿制或模仿,特别是在功能、界面等方面,如何判断是否构成侵权?该如何应对? 答:LabVIEW软件的侵权问题,尤其是在涉及到仿制或模仿其功能、界面、设计等方面࿰…...

【redis】centos7下安装redis7
在CentOS 7下安装Redis7可以通过以下两种方法实现:手动编译安装和使用YUM进行安装。 CentOS 7系统的环境和版本: $ cat /etc/centos-release CentOS Linux release 7.9.2009 (Core)手动编译安装 参考官方文档:https://redis.io/docs/lates…...
)
[network]回顾:集线器(Hub)
集线器(Hub)的发明是计算机网络发展史上的一个重要里程碑。它最初的设计目的是为了解决局域网(LAN)中多台计算机共享网络资源的需求。 #mermaid-svg-OAmOmKYGAXoglS5z {font-family:"trebuchet ms",verdana,arial,sans-…...

79 Openssl3.0 RSA公钥加密数据
1 引言 最近不小心用到了openssl3.0,项目中需要使用rsa非对称加解密算法,所以把openssl3.0使用公钥加密数据的函数调用摸了一遍。 之所以记录此篇文章,是因为网络上大多数是openssl3.0以前的版本的函数接口,而openssl3.0之后已经丢…...
)
EFCore HasDefaultValueSql (续2 HasComputedColumnSql)
前情:EFCore HasDefaultValueSql EFCore HasDefaultValueSql (续1 ValueGeneratedOnAdd)-CSDN博客 小伙伴在使用 HasDefaultValueSql 时,对相关的 ValueGeneratedOnAdd, HasComputedColumnSql 也有了疑问: HasComputedColumnSql 对于计算…...
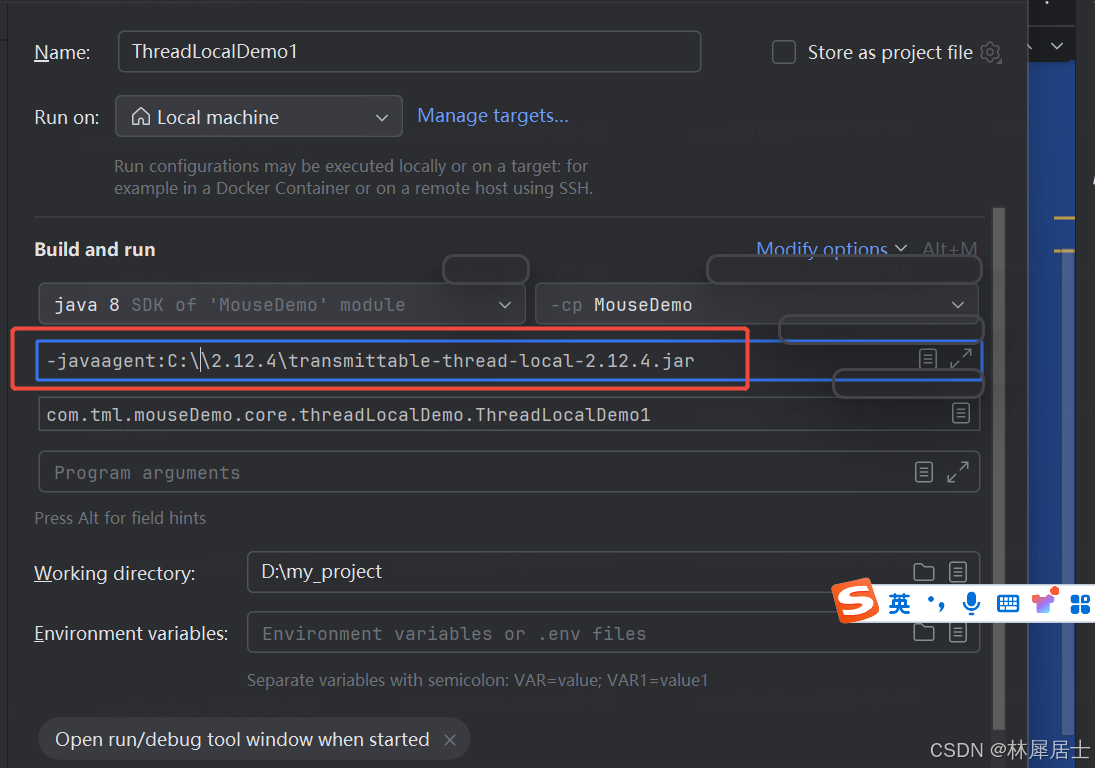
阿里巴巴TransmittableThreadLocal使用指南
前言 ThreadLocal在上下文的数据传输上非常的方便和简洁。工业实践中,比较常用的有三个,ThreadLocal、InheritableThreadLocal、TransmittableThreadLocal,那么他们三个之间有什么区别呢? 常见的三种ThreadLocal比较 ThreadLoc…...
)
ubuntu20下编译linux1.0 (part1)
author: hjjdebug date: 2025年 01月 09日 星期四 15:56:15 CST description: ubuntu20下编译linux1.0 (part1) 该博客记录了新gcc编译旧代码可能碰到的问题和解决办法, 可留作参考 操作环境: ubuntu20 $ gcc --version gcc (Ubuntu 9.4.0-1ubuntu1~20.04.2) 9.4.0 $ as --vers…...

欧拉公式和傅里叶变换
注:英文引文机翻,未校。 中文引文未整理去重,如有异常,请看原文。 Euler’s Formula and Fourier Transform Posted byczxttkl October 7, 2018 Euler’s formula states that e i x cos x i sin x e^{ix} \cos{x} i …...
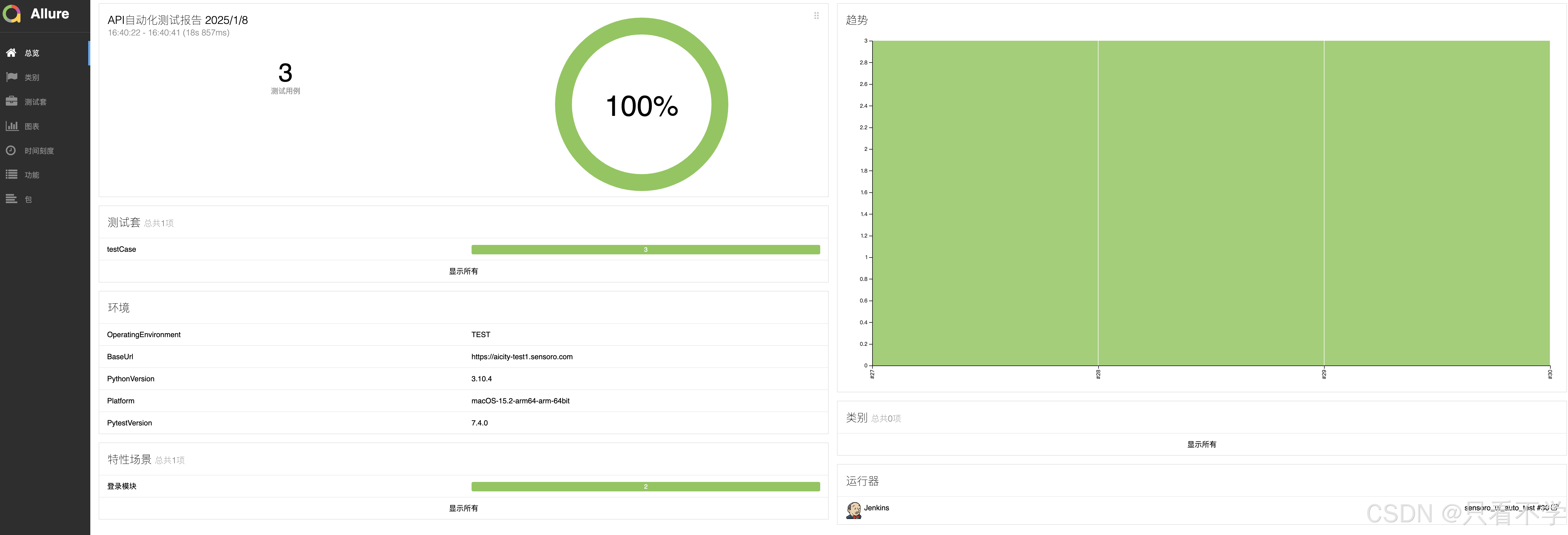
Jenkins内修改allure报告名称
背景: 最近使用Jenkins搭建自动化测试环境时,使用Jenkins的allure插件生成的报告,一直显示默认ALLURE REPORT,想自定义成与项目关联的名称,如图所示,很明显自定义名称显得高大上些,之前…...
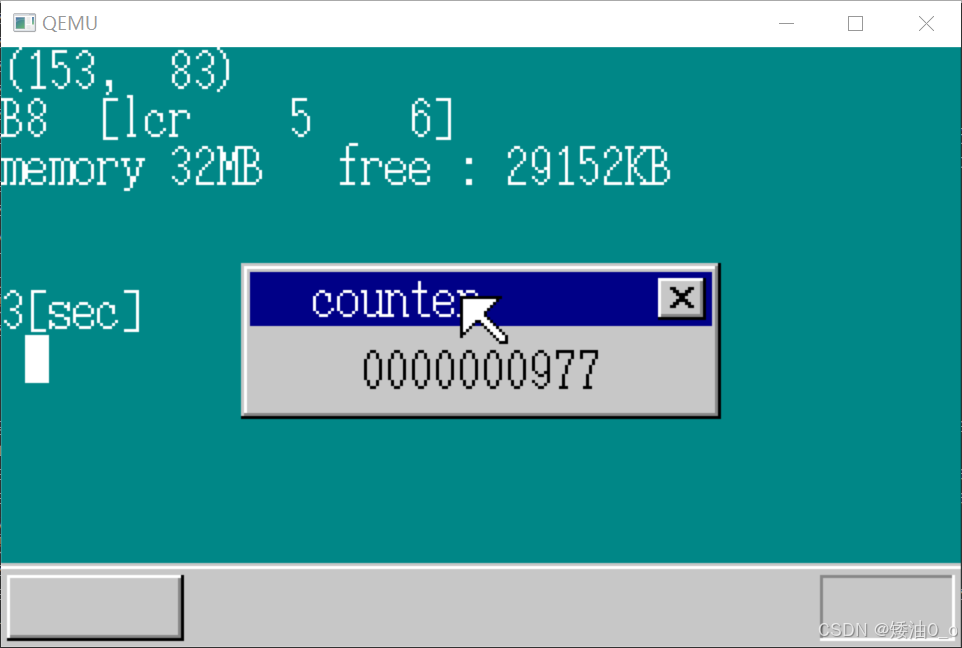
30天开发操作系统 第 12 天 -- 定时器 v1.0
前言 定时器(Timer)对于操作系统非常重要。它在原理上却很简单,只是每隔一段时间(比如0.01秒)就发送一个中断信号给CPU。幸亏有了定时器,CPU才不用辛苦地去计量时间。……如果没有定时器会怎么样呢?让我们想象一下吧。 假如CPU看不到定时器而仍想计量时…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
