2024 China Collegiate Programming Contest (CCPC) Zhengzhou Onsite 基础题题解
今天先发布基础题的题解,明天再发布铜牌题和银牌题的题解
L. Z-order Curve

思路:这题目说了,上面那一行,只有在偶数位才有可能存在1,那么一定存在这样的数,0 ,1,100, 10000,那么反之,我们的数列是行的二倍,因此会出现10,1000,100000这样的数,因此,就可以发现,其实组成的数也是由二进制数递推的,因此我们可以从高位到低位逐步去找,如果相同且为1就变成0,如果不同就直接结束,输出L即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int l,r;
void solve()
{cin>>l>>r;for(int i=61;i>=0;i--){int bitl=(l>>i)&1;int bitr=(r>>i)&1;if(bitl==bitr&&bitl==1){l-=(1LL<<i);r-=(1LL<<i);}else if(bitl!=bitr){cout<<l<<"\n";return ;}}
}
signed main()
{cin>>t;while(t--){solve();}return 0;
}F. Infinite Loop

思路:这题有一个比较恶心的地方,就是说从1小时开始,实际上是从0小时开始计算,然后我们去计算公差是多少,我们现将所有的bi加在一起为sum,然后取sum和k的较大值作为公差,然后去对题目进行分析,我们会发现,从第二天开始,就去进行等差数列了,因此我们只需要计算出来第一天和第二天在什么时候完成即可,还有一个特判就是要对小时特判,如果小时是0,那么天数-1,小时+k
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,k,q;
int a[200005];
int b[200005];
int ans1[200005];
int ans2[200005];
int d;
int flag,x;
signed main()
{cin>>n>>k>>q;for(int i=1;i<=n;i++){cin>>a[i]>>b[i];a[i]-=1;d+=b[i];}d=max(d,k);int t=0;for(int i=1;i<=n;i++){ans1[i]=max(t,a[i])+b[i];t=ans1[i];}for(int i=1;i<=n;i++){a[i]+=k;}for(int i=1;i<=n;i++){ans2[i]=max(t,a[i])+b[i];t=ans2[i];}for(int i=1;i<=q;i++){cin>>flag>>x;if(flag==1){int day=ans1[x]/k;int hour=ans1[x]%k; if(hour==0){day-=1;hour+=k;}cout<<day+1<<" "<<hour<<"\n";}else{int time=ans2[x]+(flag-2)*d;int day=time/k;int hour=time%k; if(hour==0){day-=1;hour+=k;}cout<<day+1<<" "<<hour<<"\n";}}return 0;
}B. Rolling Stones

思路:很板的一个广搜,只需要找到翻转之后,每个面上面是什么就可以了,同时要确保翻转的时候翻转过去的面,等于那个底面上的值
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[205][205];
struct node{int x,y;int qian;int zuo;int you;int di;int tmp;
};
deque<node> q;
int vis[205][205];
int ans[205][205];
int fx,fy;
void bfs()
{while(!q.empty()){node test=q.front();q.pop_front();int x=test.x;int y=test.y;
// cout<<x<<" "<<y<<"\n";
// cout<<test.qian<<" "<<test.zuo<<" "<<test.you<<" "<<test.di<<"\n";if(y%2==0){if(vis[x][y-1]==0&&y-1>=1&&y-1<=2*x-1&&a[x][y-1]==test.zuo)//向左移动{vis[x][y-1]=1;q.push_back((node){x,y-1,test.you,test.qian,test.di,test.zuo,test.tmp+1});ans[x][y-1]=test.tmp+1;} if(vis[x][y+1]==0&&y+1>=1&&y+1<=2*x-1&&a[x][y+1]==test.you)//向右移动{vis[x][y+1]=1;q.push_back((node){x,y+1,test.zuo,test.di,test.qian,test.you,test.tmp+1});ans[x][y+1]=test.tmp+1;} if(vis[x-1][y-1]==0&&y-1>=1&&y-1<=2*(x-1)-1&&x-1>=1&&x-1<=n&&a[x-1][y-1]==test.qian)//向上移动{vis[x-1][y-1]=1;q.push_back((node){x-1,y-1,test.di,test.zuo,test.you,test.qian,test.tmp+1});ans[x-1][y-1]=test.tmp+1;}}else{if(vis[x][y-1]==0&&y-1>=1&&y-1<=2*x-1&&a[x][y-1]==test.zuo)//向左移动{vis[x][y-1]=1;q.push_back((node){x,y-1,test.you,test.qian,test.di,test.zuo,test.tmp+1});ans[x][y-1]=test.tmp+1;} if(vis[x][y+1]==0&&y+1>=1&&y+1<=2*x-1&&a[x][y+1]==test.you)//向右移动{vis[x][y+1]=1;q.push_back((node){x,y+1,test.zuo,test.di,test.qian,test.you,test.tmp+1});ans[x][y+1]=test.tmp+1;} if(vis[x+1][y+1]==0&&y+1>=1&&y+1<=2*(x+1)-1&&x+1>=1&&x+1<=n&&a[x+1][y+1]==test.qian)//向下移动{vis[x+1][y+1]=1;q.push_back((node){x+1,y+1,test.di,test.zuo,test.you,test.qian,test.tmp+1});ans[x+1][y+1]=test.tmp+1;}}}
}
signed main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=2*i-1;j++){cin>>a[i][j];}}cin>>fx>>fy;if(fx==1&&fy==1){cout<<0<<"\n";return 0;}q.push_back((node){1,1,2,1,3,4,0});vis[1][1]=1;bfs();if(ans[fx][fy]==0){cout<<"-1\n";}else{cout<<ans[fx][fy]<<"\n";}return 0;
}M. Rejection Sampling

思路:这题一开始看起来其实是有点儿乱的,不知道在说什么,而且也不知道到底要操作什么,但是仔细阅读后会发现,那个S的概率就是C(n,k)*pi^k+(1-pi)^(n-k),若想要满足题目中的S与ai乘正比的话,我们需要满足pi/(1-pi)与ai成正比,我们可以将比例系数C设为c,因此我们可以得到式子
pi/(1-pi)=c*ai;
可以得到pi=c*ai/(1+c*ai),可知,pi关于c单调递增
c=pi/((1-pi)*ai),我们可以去二分c然后去判断pi的和是否是k
然后就解决了
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, k;
long double a[100005];
bool check(long double c)
{long double ans=0;long double x;for(int i=1;i<=n;i++) {x =(c*a[i])/(1.00+c*a[i]);ans+=x;}return ans<=k;
}
signed main()
{cin>>n>>k;for (int i=1;i<=n;i++) {cin>>a[i];}long double l=0.0;long double r=1e15;for (int i=1;i<=200;i++) {long double mid=(l+r)/2;if (check(mid)) {l=mid;} else {r=mid;}}cout<<fixed<<setprecision(10);for (int i = 1;i<=n;i++) {cout<<(long double)(l*a[i])/(1.00+l*a[i])<<"\n";}return 0;
}相关文章:

2024 China Collegiate Programming Contest (CCPC) Zhengzhou Onsite 基础题题解
今天先发布基础题的题解,明天再发布铜牌题和银牌题的题解 L. Z-order Curve 思路:这题目说了,上面那一行,只有在偶数位才有可能存在1,那么一定存在这样的数,0 ,1,100, 10000,那么反之,我们的数…...

halcon3d 如何计算平面法向量!确实很简单
这个问题其实一直困扰了我很长时间,之前是怎么算的呢 对于一个平面,我会先求它的fit_primitives_object_model_3d去将它拟合,接下来用surface_normals_object_model_3d 算子生成它的法线,后用get_object_model_3d_params (ObjectModel3DNormals, ‘point_normal_x’, GenP…...
浅尝Appium自动化框架
浅尝Appium自动化框架 Appium自动化框架介绍Appium原理Appium使用安装平台驱动实战 坑 Appium自动化框架介绍 Appium 是一个开源的自动化测试框架,最初设计用于移动应用的测试,但现在它也扩展了对桌面端应用的支持。Appium 使得自动化测试变得更加简单&…...

网络安全测评技术与标准
网络安全测评概况 网络安全测评是网络信息系统和IT技术产品的安全质量保障。本节主要阐述网络安全测评的概念,给出网络安全测评的发展状况。 18.1.1 网络安全测评概念 网络安全测评是指参照一定的标准规范要求,通过一系列的技术和管理方法,获…...
【经典神经网络架构解析篇】【1】LeNet网络详解:模型结构解析、优点、实现代码
《------往期经典推荐------》 一、AI应用软件开发实战专栏【链接】 项目名称项目名称1.【人脸识别与管理系统开发】2.【车牌识别与自动收费管理系统开发】3.【手势识别系统开发】4.【人脸面部活体检测系统开发】5.【图片风格快速迁移软件开发】6.【人脸表表情识别系统】7.【…...

KGA:AGeneral Machine Unlearning Framework Based on Knowledge Gap Alignment
文章目录 摘要1 引言2 相关工作3 符号与定义4 我们的 KGA 框架4.1 KGA框架知识差距对齐目标 4.2 KGA在自然语言处理任务中的应用文本分类机器翻译响应生成 5 实验设置数据集评估指标参数设置比较方法 6 实验结果6.1 主要比较结果6.2 KGA 的优越性分析降低语言模型概率比较 6.3 …...

GelSight Mini视触觉传感器凝胶触头升级:增加40%耐用性,拓展机器人与触觉AI 应用边界
马萨诸塞州沃尔瑟姆-2025年1月6日-触觉智能技术领军企业Gelsight宣布,旗下Gelsight Mini视触觉传感器迎来凝胶触头的更新。经内部测试,新Gel凝胶触头耐用性提升40%,外观与触感与原凝胶触头保持一致。此次升级有效满足了客户在机器人应用中对设…...

springboot整合admin
1. 添加依赖 首先,在你的admin服务端pom.xml文件中添加Spring Boot Admin的依赖: <dependency><groupId>de.codecentric</groupId><artifactId>spring-boot-admin-starter-server</artifactId><version>2.5.4<…...

OS--常见的网络模型(包含IO多路复用的原理)
网络模型 IO模型主要就是用户空间和内核空间数据交换的形式。 IO模型 阻塞 I/O 模型(Blocking I/O) 应用程序发起 I/O 请求后,会被阻塞,直到 I/O 操作完成。 非阻塞 I/O 模型(Non-blocking I/O) 应用程序…...
预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异)
LCE(Local Cascade Ensemble)预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异
LCE(Local Cascade Ensemble)预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异。以下是对两者的比较: 一、效果比较 LCE模型: 优势:LCE结合了随机森林和XGBoost的优势&a…...

【mysql】约束的基本使用
文章目录 1. PRIMARY KEY 约束1.1 作用1.2 关键字1.3 特点1.4 添加主键约束1.5 关于复合主键1.6 删除主键约束 2. 自增列:AUTO_INCREMENT2.1 作用2.2 关键字2.3 特点和要求2.4 如何指定自增约束2.5 如何删除自增约束2.6 MySQL 8.0新特性—自增变量的持久化 3. FOREI…...

EasyExcel(二)导出Excel表自动换行和样式设置
EasyExcel(一)导出Excel表列宽自适应 背景 在上一篇文章中解决导出列宽自适应,然后也解决了导出列宽不可超过255的问题。但是实际应用场景中仍然会有导出数据的长度超过列宽255。这时导出效果就会出现如下现象: 多出列宽宽度的内容会浮出来,影响后边列数据的显示。 解决…...

农产品直播带货方案拆解
作为一名经验丰富的营销策划人道叔,今天我来拆解一下咱们4A营销广告圈的这份《直播天府川农好物带货方案》,让你能学到很多实用的策略和技巧,直接应用到你的策划工作中去。 首先,咱们看看背景分析。 助农直播现在可是个大热门&a…...

“**H5**” 和 “**响应式**” 是前端开发中常见的术语,但它们的概念和使用场景有所不同
“H5” 和 “响应式” 是前端开发中常见的术语,但它们的概念和使用场景有所不同。以下是它们的区别以及为什么为移动端开发的页面通常被称为 “H5” 的解释: 1. 为什么为移动端开发的叫 “H5”? “H5” 是 HTML5 的简称,HTML5 是…...
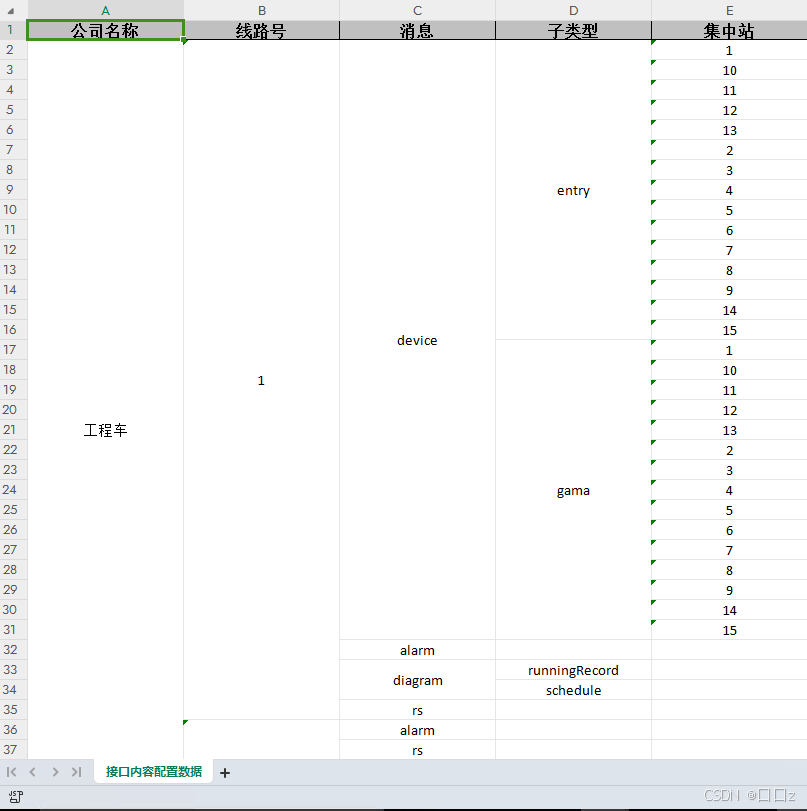
基于EasyExcel实现通用版一对一、一对多、多层嵌套结构数据导出并支持自动合并单元格
接口功能 通用 支持一对一数据结构导出 支持一对多数据结构导出 支持多层嵌套数据结构导出 支持单元格自动合并 原文来自:https://blog.csdn.net/qq_40980205/article/details/136564176 新增及修复 基于我自己的使用场景,新增并能修复一下功能&#x…...

Java堆内存分析
(一)、线上查看堆内存统计 # 命令用于打印堆内存中每个类的实例数量及其占用的内存,并且只包括活动对象(即存活的对象) jmap -histo:live <pid># 输出到文件方便查看 jmap -histo:live 12345 > aaa.txt(二)、下载dump文件࿰…...
maven高级(day15)
Maven 是一款构建和管理 Java 项目的工具 分模块设计与开发 所谓分模块设计,顾名思义指的就是我们在设计一个 Java 项目的时候,将一个 Java 项目拆分成多 个模块进行开发。 分模块设计我们在进行项目设计阶段,就可以将一个大的项目拆分成若干…...
:乘法器)
计算机组成原理(九):乘法器
乘法器原理 乘法器的工作原理可以用二进制乘法来说明。二进制乘法和十进制乘法类似,通过部分积的累加得到结果。 部分积的生成 在二进制乘法中,每一位的乘积是两个二进制数位的 与运算(0 0 0,1 0 0,0 1 0&…...

python【输入和输出】
Python 有三种输出值的方式: 表达式语句print() 函数使用文件对象的 write() 方法,标准输出文件可以用 sys.stdout 引用。 ① 将输出的值转成字符串,可以使用 repr() 或 str() 函数来实现: str(): 函数返回一个用户易…...
)
2024年华为OD机试真题-判断一组不等式是否满足约束并输出最大差-Python-OD统一考试(E卷)
最新华为OD机试考点合集:华为OD机试2024年真题题库(E卷+D卷+C卷)_华为od机试题库-CSDN博客 每一题都含有详细的解题思路和代码注释,精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看,发现新题及时跟新。 题目描述: 给定一组不等式…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...

NineData数据库DevOps功能全面支持百度智能云向量数据库 VectorDB,助力企业 AI 应用高效落地
NineData 的数据库 DevOps 解决方案已完成对百度智能云向量数据库 VectorDB 的全链路适配,成为国内首批提供 VectorDB 原生操作能力的服务商。此次合作聚焦 AI 开发核心场景,通过标准化 SQL 工作台与细粒度权限管控两大能力,助力企业安全高效…...

TMC2226超静音步进电机驱动控制模块
目前已经使用TMC2226量产超过20K,发现在静音方面做的还是很不错。 一、TMC2226管脚定义说明 二、原理图及下载地址 一、TMC2226管脚定义说明 引脚编号类型功能OB11电机线圈 B 输出 1BRB2线圈 B 的检测电阻连接端。将检测电阻靠近该引脚连接到地。使用内部检测电阻时,将此引…...
