【Javascript Day5】for循环及典型案例
for 循环
// 语法: for( 开始 ; 结束 ; 步长 ){ 循环体 }
// for( var i = 循环初始值 ; i的循环范围 ; i的增加或减少规则 ){ 循环体 }
// 死循环
// for(;;){
// console.log("for循环");
// }
// 循环打印10次
for(var i=0; i<10 ; i++){
console.log("for循环");
}
// 计算 1~100的累加(求和)结果
var sum = 0;
for (var i = 1; i <= 100; i++) {
// sum = sum + i;
sum += i;
}
console.log(sum);
// 算法:将代码通过固定的逻辑或者公式进行简化,提供程序的运行效率
// 连续数值相加公式 : (首位+末尾)*(位数/2)
var sum1 = (1+100)*(100/2);
console.log(sum1);
多重循环:循环嵌套
// 内层循环的循环次数 = 自身循环的次数*外层循环次数
// for (var i = 0; i < 10; i++) {
// for (var j = 0; j < 10; j++) {
// console.log(i,j);
// }
// }
练习
1.不限位数的回文数
var flag = true; // 默认认为是回文数// 不限位数的回文数var num = 1234321;// length是字符串的功能,所有先转换为字符串,再获取var size = (num+"").length;// 计算出需要判断次数var end = parseInt(size/2);for (var i = 1; i <= end; i++) {// console.log( num%10 ); // 10**1// console.log( num%100 ); // 10**2// console.log( num%1000 ); // 10**3var a = num%(10**i); // 32for (var j = 1; j < i; j++) {a = parseInt(a / 10);}// console.log( parseInt(num/1000000) ); // 10 ** (7-1)// console.log( parseInt(num/100000) ); // 10 ** (7-2)// console.log( parseInt(num/10000) ); // 10 ** (7-3)var b = parseInt( num / ( 10**(size-i) ) );b = b % 10;console.log(a,b,a==b);if(a!=b){flag = false;}}console.log(num, flag?"是回文数":"不是回文数" );2.入职薪水10K,每年涨幅5%,50年后工资多少?
<script>var sum =10000;for( var i = 1 ; i <= 50 ;i++){sum *= 1.05;}console.log(sum)</script>3.矩形*号
<script>var i;var sum = "";for( i=1 ; i<= 18; i++){sum += "*";if(i % 6 == 0){sum += "\n";}}console.log(sum);</script>效果
4.九九乘法表
<script>var i = 1 ;var j ;var sum ="";for(j =1 ;j <= i; j++){for (i = 1; i <= j; i++) {sum += (i + "*" + j + "=" + (i*j) + " ");}sum += "\n";if(j == 9){break;}}console.log(sum);</script>效果

5.三位水仙花数
var num = prompt("请输入一个数");var a = (num % 100);var b = (num - a);var c = (b / 100);var d = parseInt((num % 100)/10);if(isNaN(num)){alert(`${num}不是数值!`)}else if(num == null||num==''){alert("用户未输入") }else if(num <100 || num >=1000){alert("只能输入三位数,请重新输入!")}else if((((num %100) % 10) % 1) != 0){alert("不能输入小数,请重新输入!")}else if((c**3 +(a % 10)**3 + d**3) == num*1){alert(`${num}是水仙花数`)}else if((c**3 +(a % 10)**3 + d**3) != num*1){alert(`${num}不是水仙花数`)}相关文章:

【Javascript Day5】for循环及典型案例
for 循环 // 语法: for( 开始 ; 结束 ; 步长 ){ 循环体 } // for( var i 循环初始值 ; i的循环范围 ; i的增加或减少规则 ){ 循环体 } // 死循环 // for(;;){ // console.log("for循环"); // } // 循环打…...

#渗透测试#网络安全#一文了解什么是shell反弹!!!
免责声明 本教程仅为合法的教学目的而准备,严禁用于任何形式的违法犯罪活动及其他商业行为,在使用本教程前,您应确保该行为符合当地的法律法规,继续阅读即表示您需自行承担所有操作的后果,如有异议,请立即停…...

《解锁图像的语言密码:Image Caption 开源神经网络项目全解析》
《解锁图像的语言密码:Image Caption 开源项目全解析》 一、开篇:AI 看图说话时代来临二、走进 Image Caption 开源世界三、核心技术拆解:AI 如何学会看图说话(一)深度学习双雄:CNN 与 RNN(二&a…...

抢占欧洲电商高地,TikTok 运营专线成 “秘密武器”
在当今数字化浪潮席卷全球的时代,社交媒体平台已成为商业拓展的关键阵地,TikTok 更是其中的闪耀新星。近日,一则重磅消息引发行业关注:TikTok 正计划于 2025 年初进军荷兰电商市场。这一战略布局,不仅彰显了 TikTok 对…...

人工智能-数据分析及特征提取思路
1、概况 基于学生行为数据预测是否涉黄、涉黑等。 2.数据分析 数据分析的意义包括得到数据得直觉、发掘潜在的结构、提取重要的变量、删除异常值、检验潜在的假设和建立初步的模型。 2.1数据质量分析 2.1.1数据值分析 查看数据类型: 首先明确各字段的数据类型…...

2024 China Collegiate Programming Contest (CCPC) Zhengzhou Onsite 基础题题解
今天先发布基础题的题解,明天再发布铜牌题和银牌题的题解 L. Z-order Curve 思路:这题目说了,上面那一行,只有在偶数位才有可能存在1,那么一定存在这样的数,0 ,1,100, 10000,那么反之,我们的数…...

halcon3d 如何计算平面法向量!确实很简单
这个问题其实一直困扰了我很长时间,之前是怎么算的呢 对于一个平面,我会先求它的fit_primitives_object_model_3d去将它拟合,接下来用surface_normals_object_model_3d 算子生成它的法线,后用get_object_model_3d_params (ObjectModel3DNormals, ‘point_normal_x’, GenP…...
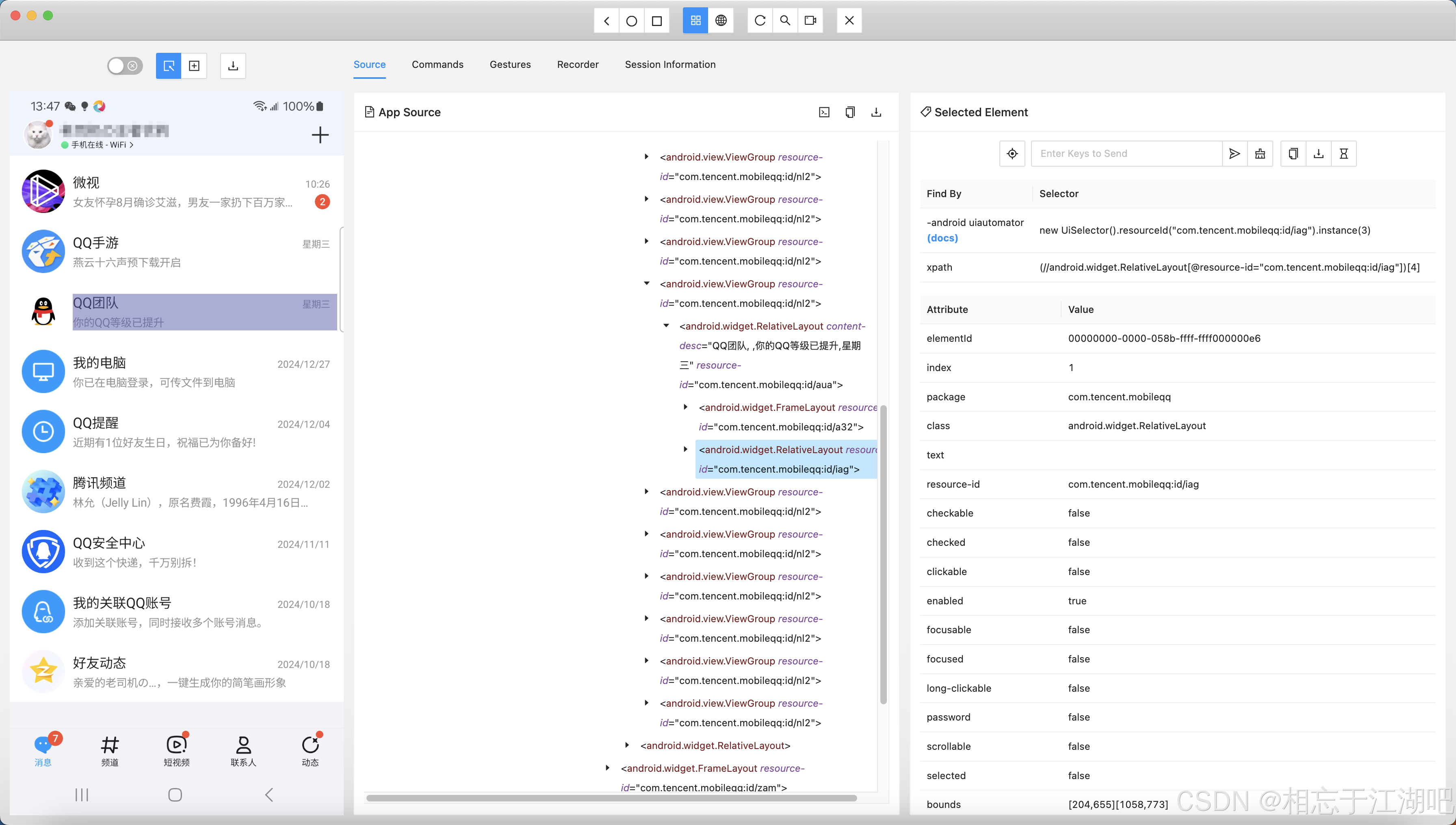
浅尝Appium自动化框架
浅尝Appium自动化框架 Appium自动化框架介绍Appium原理Appium使用安装平台驱动实战 坑 Appium自动化框架介绍 Appium 是一个开源的自动化测试框架,最初设计用于移动应用的测试,但现在它也扩展了对桌面端应用的支持。Appium 使得自动化测试变得更加简单&…...

网络安全测评技术与标准
网络安全测评概况 网络安全测评是网络信息系统和IT技术产品的安全质量保障。本节主要阐述网络安全测评的概念,给出网络安全测评的发展状况。 18.1.1 网络安全测评概念 网络安全测评是指参照一定的标准规范要求,通过一系列的技术和管理方法,获…...
【经典神经网络架构解析篇】【1】LeNet网络详解:模型结构解析、优点、实现代码
《------往期经典推荐------》 一、AI应用软件开发实战专栏【链接】 项目名称项目名称1.【人脸识别与管理系统开发】2.【车牌识别与自动收费管理系统开发】3.【手势识别系统开发】4.【人脸面部活体检测系统开发】5.【图片风格快速迁移软件开发】6.【人脸表表情识别系统】7.【…...

KGA:AGeneral Machine Unlearning Framework Based on Knowledge Gap Alignment
文章目录 摘要1 引言2 相关工作3 符号与定义4 我们的 KGA 框架4.1 KGA框架知识差距对齐目标 4.2 KGA在自然语言处理任务中的应用文本分类机器翻译响应生成 5 实验设置数据集评估指标参数设置比较方法 6 实验结果6.1 主要比较结果6.2 KGA 的优越性分析降低语言模型概率比较 6.3 …...

GelSight Mini视触觉传感器凝胶触头升级:增加40%耐用性,拓展机器人与触觉AI 应用边界
马萨诸塞州沃尔瑟姆-2025年1月6日-触觉智能技术领军企业Gelsight宣布,旗下Gelsight Mini视触觉传感器迎来凝胶触头的更新。经内部测试,新Gel凝胶触头耐用性提升40%,外观与触感与原凝胶触头保持一致。此次升级有效满足了客户在机器人应用中对设…...

springboot整合admin
1. 添加依赖 首先,在你的admin服务端pom.xml文件中添加Spring Boot Admin的依赖: <dependency><groupId>de.codecentric</groupId><artifactId>spring-boot-admin-starter-server</artifactId><version>2.5.4<…...

OS--常见的网络模型(包含IO多路复用的原理)
网络模型 IO模型主要就是用户空间和内核空间数据交换的形式。 IO模型 阻塞 I/O 模型(Blocking I/O) 应用程序发起 I/O 请求后,会被阻塞,直到 I/O 操作完成。 非阻塞 I/O 模型(Non-blocking I/O) 应用程序…...
预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异)
LCE(Local Cascade Ensemble)预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异
LCE(Local Cascade Ensemble)预测模型和LSTM(Long Short-Term Memory)模型在效果和特点上存在显著差异。以下是对两者的比较: 一、效果比较 LCE模型: 优势:LCE结合了随机森林和XGBoost的优势&a…...

【mysql】约束的基本使用
文章目录 1. PRIMARY KEY 约束1.1 作用1.2 关键字1.3 特点1.4 添加主键约束1.5 关于复合主键1.6 删除主键约束 2. 自增列:AUTO_INCREMENT2.1 作用2.2 关键字2.3 特点和要求2.4 如何指定自增约束2.5 如何删除自增约束2.6 MySQL 8.0新特性—自增变量的持久化 3. FOREI…...

EasyExcel(二)导出Excel表自动换行和样式设置
EasyExcel(一)导出Excel表列宽自适应 背景 在上一篇文章中解决导出列宽自适应,然后也解决了导出列宽不可超过255的问题。但是实际应用场景中仍然会有导出数据的长度超过列宽255。这时导出效果就会出现如下现象: 多出列宽宽度的内容会浮出来,影响后边列数据的显示。 解决…...

农产品直播带货方案拆解
作为一名经验丰富的营销策划人道叔,今天我来拆解一下咱们4A营销广告圈的这份《直播天府川农好物带货方案》,让你能学到很多实用的策略和技巧,直接应用到你的策划工作中去。 首先,咱们看看背景分析。 助农直播现在可是个大热门&a…...

“**H5**” 和 “**响应式**” 是前端开发中常见的术语,但它们的概念和使用场景有所不同
“H5” 和 “响应式” 是前端开发中常见的术语,但它们的概念和使用场景有所不同。以下是它们的区别以及为什么为移动端开发的页面通常被称为 “H5” 的解释: 1. 为什么为移动端开发的叫 “H5”? “H5” 是 HTML5 的简称,HTML5 是…...
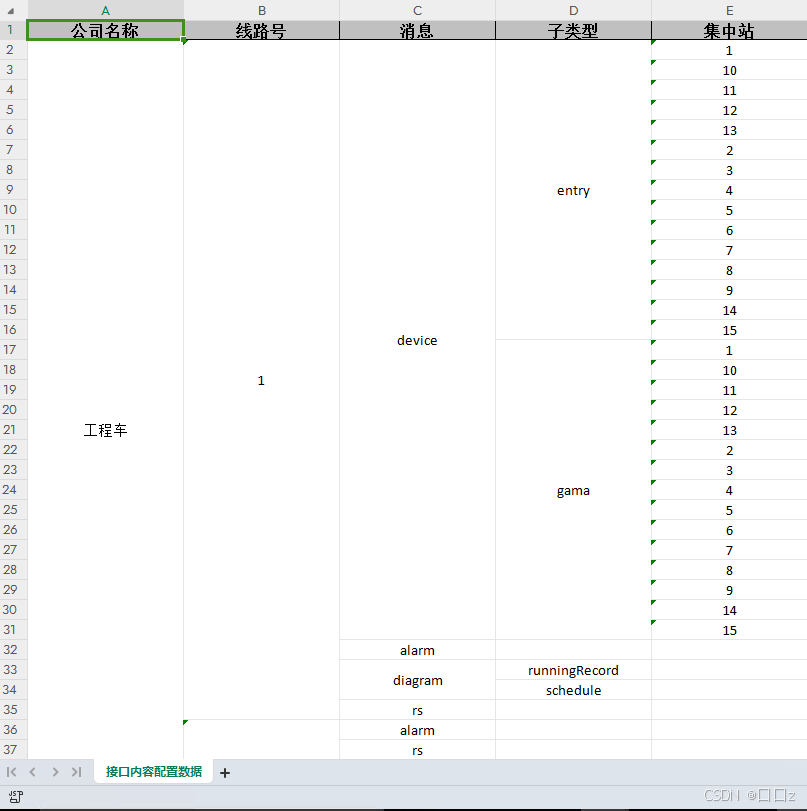
基于EasyExcel实现通用版一对一、一对多、多层嵌套结构数据导出并支持自动合并单元格
接口功能 通用 支持一对一数据结构导出 支持一对多数据结构导出 支持多层嵌套数据结构导出 支持单元格自动合并 原文来自:https://blog.csdn.net/qq_40980205/article/details/136564176 新增及修复 基于我自己的使用场景,新增并能修复一下功能&#x…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

