核密度估计(Kernel Density Estimation, KDE)是一种非参数统计方法
一、核密度估计
核密度估计(Kernel Density Estimation, KDE)是一种非参数统计方法,用于估计随机变量的概率密度函数。它通过将每个数据点周围的核函数叠加,生成平滑的密度曲线。以下是其核心要点:
1. 基本概念
- 非参数方法:无需假设数据分布的具体形式。
- 核函数:常用的有高斯核、均匀核等,决定每个数据点对密度估计的影响。
- 带宽(Bandwidth):控制核函数的宽度,影响估计的平滑度。
2. 数学表达
给定样本 X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn,核密度估计公式为:
f ^ ( x ) = 1 n h ∑ i = 1 n K ( x − X i h ) \hat{f}(x) = \frac{1}{n h} \sum_{i=1}^{n} K\left(\frac{x - X_i}{h}\right) f^(x)=nh1i=1∑nK(hx−Xi)
其中:
- f ^ ( x ) \hat{f}(x) f^(x)是在点 x x x处的密度估计。
- K ( ⋅ ) K(\cdot) K(⋅)是核函数。
- h h h是带宽参数。
- n n n是样本数量。
3. 核函数选择
常见的核函数包括:
- 高斯核: K ( u ) = 1 2 π e − 1 2 u 2 K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}u^2} K(u)=2π1e−21u2
- 均匀核: K ( u ) = 1 2 I ( ∣ u ∣ ≤ 1 ) K(u) = \frac{1}{2} \mathbb{I}(|u| \leq 1) K(u)=21I(∣u∣≤1)
- Epanechnikov核: K ( u ) = 3 4 ( 1 − u 2 ) I ( ∣ u ∣ ≤ 1 ) K(u) = \frac{3}{4}(1 - u^2) \mathbb{I}(|u| \leq 1) K(u)=43(1−u2)I(∣u∣≤1)
4. 带宽选择
带宽 h h h的选择至关重要,常见方法有:
- 规则选择:如Silverman规则。
- 交叉验证:通过最小化均方误差选择最优带宽。
5. 应用场景
- 数据可视化:生成平滑的密度曲线。
- 异常检测:识别低密度区域的异常点。
- 模式识别:发现数据中的多峰分布。
6. 优缺点
- 优点:
- 无需假设数据分布。
- 能生成平滑的密度估计。
- 缺点:
- 计算复杂度较高。
- 带宽选择对结果影响大。
7. 实现工具
- Python:
scipy.stats.gaussian_kde、seaborn.kdeplot - R:
density()函数
示例代码(Python)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde# 生成样本数据
data = np.random.normal(0, 1, 1000)# 核密度估计
kde = gaussian_kde(data)
x = np.linspace(-5, 5, 1000)
y = kde(x)# 绘制结果
plt.plot(x, y, label='KDE')
plt.hist(data, bins=30, density=True, alpha=0.5, label='Histogram')
plt.legend()
plt.show()
核密度估计是一种灵活且强大的工具,适用于多种数据分析和可视化任务。合理选择核函数和带宽是获得准确估计的关键。
二、常见核函数及选择方法
选择合适的核函数是核密度估计(KDE)中的重要步骤,虽然核函数的选择对结果的影响通常不如带宽选择显著,但在某些情况下,核函数的选择仍然会影响估计的平滑度和准确性。以下是选择适当核函数的一些指导原则和方法:
1. 常见核函数及其特性
不同的核函数具有不同的形状和特性,常见核函数包括:
- 高斯核(Gaussian Kernel):
- 公式: K ( u ) = 1 2 π e − 1 2 u 2 K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}u^2} K(u)=2π1e−21u2
- 特点:无限支撑,平滑性好,适用于大多数情况。
- 均匀核(Uniform Kernel):
- 公式: K ( u ) = 1 2 I ( ∣ u ∣ ≤ 1 ) K(u) = \frac{1}{2} \mathbb{I}(|u| \leq 1) K(u)=21I(∣u∣≤1)
- 特点:简单,但不连续,适用于离散数据。
- Epanechnikov核:
- 公式: K ( u ) = 3 4 ( 1 − u 2 ) I ( ∣ u ∣ ≤ 1 ) K(u) = \frac{3}{4}(1 - u^2) \mathbb{I}(|u| \leq 1) K(u)=43(1−u2)I(∣u∣≤1)
- 特点:有限支撑,计算效率高,平滑性较好。
- 三角核(Triangular Kernel):
- 公式: K ( u ) = ( 1 − ∣ u ∣ ) I ( ∣ u ∣ ≤ 1 ) K(u) = (1 - |u|) \mathbb{I}(|u| \leq 1) K(u)=(1−∣u∣)I(∣u∣≤1)
- 特点:有限支撑,平滑性介于均匀核和高斯核之间。
2. 选择核函数的原则
- 平滑性需求:如果需要高度平滑的密度估计,高斯核是一个不错的选择。如果对平滑性要求不高,可以选择Epanechnikov核或三角核。
- 计算效率:有限支撑的核函数(如Epanechnikov核、均匀核)在计算上通常比无限支撑的核函数(如高斯核)更高效。
- 数据特性:根据数据的分布特性选择核函数。例如,对于具有明显边界的数据,有限支撑的核函数可能更合适。
3. 实际选择方法
- 默认选择:在许多情况下,高斯核是默认选择,因为它具有良好的平滑性和数学性质。
- 交叉验证:可以通过交叉验证的方法来选择核函数。具体步骤如下:
- 将数据分为训练集和验证集。
- 对每个候选核函数,使用训练集进行密度估计。
- 在验证集上评估密度估计的准确性(例如,使用对数似然或均方误差)。
- 选择在验证集上表现最好的核函数。
- 经验法则:根据经验或领域知识选择核函数。例如,在金融领域,高斯核常用于估计资产回报率的密度。
4. 示例代码(Python)
以下代码展示了如何使用交叉验证选择核函数:
import numpy as np
from scipy.stats import gaussian_kde
from sklearn.model_selection import KFold
from sklearn.metrics import log_loss# 生成样本数据
data = np.random.normal(0, 1, 1000)# 定义候选核函数
kernels = {'Gaussian': lambda x: gaussian_kde(x, bw_method='scott'),'Epanechnikov': lambda x: gaussian_kde(x, bw_method='scott') # 此处仅作示例,实际需实现Epanechnikov核
}# 交叉验证
kf = KFold(n_splits=5)
results = {}for name, kernel in kernels.items():log_likelihoods = []for train_index, test_index in kf.split(data):train_data = data[train_index]test_data = data[test_index]kde = kernel(train_data)log_likelihoods.append(-kde.logpdf(test_data).mean())results[name] = np.mean(log_likelihoods)# 选择最佳核函数
best_kernel = min(results, key=results.get)
print(f'Best kernel: {best_kernel} with log likelihood: {results[best_kernel]}')
选择适当的核函数需要综合考虑数据的特性、平滑性需求和计算效率。高斯核通常是默认选择,但在特定情况下,其他核函数可能更合适。通过交叉验证和经验法则,可以更科学地选择核函数。
三、无限支撑与有限支撑核函数
在核密度估计(KDE)中,“无限支撑”(Infinite Support)和“有限支撑”(Finite Support)是用来描述核函数定义域的概念。具体来说:
1. 无限支撑(Infinite Support)
-
定义:一个核函数如果在整个实数轴(即从负无穷到正无穷)上都有定义且非零,则称该核函数具有无限支撑。
-
例子:高斯核(Gaussian Kernel)是一个典型的无限支撑核函数,其公式为:
K ( u ) = 1 2 π e − 1 2 u 2 K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}u^2} K(u)=2π1e−21u2
高斯核在所有实数 u u u上都有定义且非零。 -
特点:
- 平滑性好:无限支撑的核函数通常能生成非常平滑的密度估计。
- 计算复杂度高:由于核函数在整个实数轴上都有定义,计算时需要考虑所有数据点的影响,计算量较大。
2. 有限支撑(Finite Support)
-
定义:一个核函数如果只在有限的区间内定义且非零,而在该区间外为零,则称该核函数具有有限支撑。
-
例子:Epanechnikov核和均匀核都是有限支撑核函数。Epanechnikov核的公式为:
K ( u ) = 3 4 ( 1 − u 2 ) I ( ∣ u ∣ ≤ 1 ) K(u) = \frac{3}{4}(1 - u^2) \mathbb{I}(|u| \leq 1) K(u)=43(1−u2)I(∣u∣≤1)
其中 I ( ∣ u ∣ ≤ 1 ) \mathbb{I}(|u| \leq 1) I(∣u∣≤1)是指示函数,当 ∣ u ∣ ≤ 1 |u| \leq 1 ∣u∣≤1时为1,否则为0。因此,Epanechnikov核只在区间 [ − 1 , 1 ] [-1, 1] [−1,1]内有定义且非零。 -
特点:
- 计算效率高:由于核函数只在有限区间内非零,计算时只需考虑该区间内的数据点,计算量较小。
- 平滑性较差:有限支撑的核函数生成的密度估计可能不如无限支撑核函数平滑。
3. 选择无限支撑还是有限支撑核函数
- 无限支撑核函数(如高斯核)适用于需要高度平滑密度估计的场景,尤其是在数据分布较为复杂或需要精细分析时。
- 有限支撑核函数(如Epanechnikov核)适用于计算资源有限或数据量较大的场景,因为它们计算效率更高。
4. 示例代码(Python)
以下代码展示了无限支撑(高斯核)和有限支撑(Epanechnikov核)的核密度估计:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde# 生成样本数据
data = np.random.normal(0, 1, 1000)# 高斯核(无限支撑)
kde_gaussian = gaussian_kde(data)
x = np.linspace(-5, 5, 1000)
y_gaussian = kde_gaussian(x)# Epanechnikov核(有限支撑,此处使用自定义实现)
def epanechnikov_kernel(u):return np.where(np.abs(u) <= 1, 0.75 * (1 - u**2), 0)def kde_epanechnikov(data, x, h):n = len(data)y = np.zeros_like(x)for xi in x:y += epanechnikov_kernel((xi - data) / h)return y / (n * h)h = 0.5 # 带宽
y_epanechnikov = kde_epanechnikov(data, x, h)# 绘制结果
plt.plot(x, y_gaussian, label='Gaussian KDE')
plt.plot(x, y_epanechnikov, label='Epanechnikov KDE')
plt.hist(data, bins=30, density=True, alpha=0.5, label='Histogram')
plt.legend()
plt.show()
“无限支撑”和“有限支撑”描述了核函数的定义域范围。无限支撑核函数(如高斯核)在整个实数轴上都有定义,适合需要高度平滑的密度估计;有限支撑核函数(如Epanechnikov核)只在有限区间内定义,计算效率更高。根据具体需求选择合适的核函数。
相关文章:
是一种非参数统计方法)
核密度估计(Kernel Density Estimation, KDE)是一种非参数统计方法
一、核密度估计 核密度估计(Kernel Density Estimation, KDE)是一种非参数统计方法,用于估计随机变量的概率密度函数。它通过将每个数据点周围的核函数叠加,生成平滑的密度曲线。以下是其核心要点: 1. 基本概念 非参…...

【k8s面试题2025】2、练气初期
在练气初期,灵气还比较稀薄,只能勉强在体内运转几个周天。 文章目录 简述k8s静态pod为 Kubernetes 集群移除新节点:为 K8s 集群添加新节点Kubernetes 中 Pod 的调度流程 简述k8s静态pod 定义 静态Pod是一种特殊类型的Pod,它是由ku…...

栈溢出原理
文章目录 前言一、基本示例二、分析栈1. 先不考虑gets函数的栈情况2. 分析gets函数的栈区情况 三、利用栈1. 构造字符串2. 利用漏洞 前言 栈溢出指的是程序向栈中某个变量中写入的字节数超过了这个变量本身所申请的字节数,因而导致与其相邻的栈中的变量的值被改变。…...
Jmeter如何进行多服务器远程测试
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 JMeter是Apache软件基金会的开源项目,主要来做功能和性能测试,用Java编写。 我们一般都会用JMeter在本地进行测试,但是受到单…...

2.slf4j入口
文章目录 一、故事引入二、原理探究三、SLF4JServiceProvider四、总结 一、故事引入 故事要从下面这段代码说起 public class App {private static final Logger logger LoggerFactory.getLogger(App.class);public static void main( String[] args ) throws Exception {lo…...

初学stm32 --- CAN
目录 CAN介绍 CAN总线拓扑图 CAN总线特点 CAN应用场景 CAN物理层 CAN收发器芯片介绍 CAN协议层 数据帧介绍 CAN位时序介绍 数据同步过程 硬件同步 再同步 CAN总线仲裁 STM32 CAN控制器介绍 CAN控制器模式 CAN控制器模式 CAN控制器框图 发送处理 接收处理 接收过…...

软件测试—接口测试面试题及jmeter面试题
一,接口面试题 1.接口的作用 实现前后端的交互,实现数据的传输 2.什么是接口测试 接口测试就是对系统或组件之间的接口进行测试,主要是校验数据的交换、传递和控制管理过程,以及相互逻辑关系 3.接口测试必要性 1.可以发现很…...
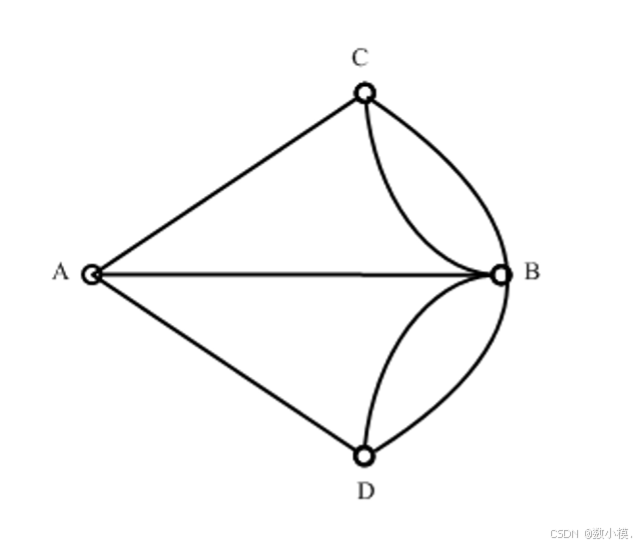
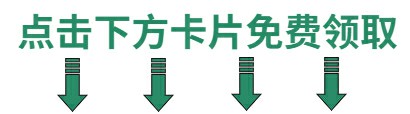
图论的起点——七桥问题
普瑞格尔河从古堡哥尼斯堡市中心流过,河中有小岛两座,筑有7座古桥,哥尼斯堡人杰地灵,市民普遍爱好数学。1736年,该市一名市民向大数学家Euler提出如下的所谓“七桥问题”: 从家里出发,7座桥每桥…...
)
嵌入式开发通讯协议大全(在写中)
目录 modbus RTU通讯协议: pmbus通讯协议: modbus RTU通讯协议: 主要应用功能: 规范了软件变量,访问功能码,给不同工程师开发的不同产品有统一的通讯标准 帧结构简单,占用带宽少,…...

webpack 4 升级 webpack 5
升级至最新的 webpack 和 webpack-cli npm run build 报错, unknown option -p 解决方案: 改成 --mode production npm run build 报错 unknown option --hide-modules 解决方案:直接移除 npm run build 报错:TypeError: Cannot a…...

oneplus3t-lineageos-16.1编译-android9, oneplus3t-lineage-14编译-android7
oneplus3t-lineage-14编译-android7 1 清华linageos镜像 x lineage-14.1-20180223-nightly-oneplus3-signed.zip ntfs分区挂载为普通用户目录 , ext4分区挂载为普通用户目录 bfsu/lineageOS镜像 ts/lingeageOS镜像 oneplus3/lineage-build-simple-manual.md, manifest-p…...

HTML中最基本的东西
本文内容的标签,将是看懂HTML的最基本之基本 ,是跟您在写文章时候一样内容。一般想掌握极其容易,但是也要懂得如何使用,过目不忘,为手熟尔。才是我们学习的最终目的。其实边看边敲都行,或者是边看边复制粘贴…...
<OS 有关>Ubuntu 24 安装 openssh-server, tailscale+ssh 慢增加
更新日志: Created on 14Jan.2025 by Dave , added openssh-server, tailescape Updated on 15Jan.2025, added "tailescape - tailscape ssh" 前期准备: 1. 更新可用软件包的数据库 2. 升级系统中所有已安装的软件包到最新版本 3. 安装 cur…...
输入输出)
神经网络常见操作(卷积)输入输出
卷积 dimd的tensor可以进行torch.nn.Convnd(in_channels,out_channels),其中nd-1,d-2对于torch.nn.Convnd(in_channels,out_channels),改变的是tensor的倒数n1维的大小 全连接 使用torch.nn.Linear(in_features,out_features,bias)实现YXWT b,其中X 的形状为 (ba…...

25/1/16 嵌入式笔记 STM32F108
输入捕获 TIM_TimeBaseInitTypeDef TIM_TimeBaseStruct; TIM_TimeBaseStruct.TIM_Period 0xFFFF; // 自动重装载值 TIM_TimeBaseStruct.TIM_Prescaler 71; // 预分频值 TIM_TimeBaseStruct.TIM_ClockDivision 0; TIM_TimeBaseStruct.TIM_CounterMode TIM_CounterMode_Up…...

mac 安装 node
brew versions node // 安装 node brew versions node14 // 安装指定版本 卸载node: sudo npm uninstall npm -g sudo rm -rf /usr/local/lib/node /usr/local/lib/node_modules /var/db/receipts/org.nodejs.* sudo rm -rf /usr/local/include/node /Users/$USER/.npm su…...

mysql常用运维命令
mysql常用运维命令 查看当前所有连接 -- 查看当前所有连接 SHOW FULL PROCESSLIST;说明: 关注State状态列,是否有锁。如果大量状态是waiting for handler commit检查磁盘是否占满关注Time耗时列,是否有慢查询关注Command列,如果…...

正则表达式学习网站
网上亲测好用的网站: Regexlearn 这个网站可以从0开始教会正则表达式的使用。 mklab 包含常用表达式,车次,超链接,号码等提取。...

gradle,adb命令行编译备忘
追踪依赖(为了解决duplicateClass…错误) gradlew.bat app:dependencies > dep-tree.txt # 分析dep-tree.txt的依赖结构,找到对应的包,可能需要做exclude控制,或者查看库issueverbose编译(我一直需要verbose) gradlew.bat assembleDebug -Dhttps.pr…...

C++:工具VSCode的编译和调试文件内容:
ubuntu24.04, vscode 配置文件 C 的环境 下载的gcc,使用命令为 sudo aptitude update sudo aptitude install build-essential -f- sudo: 以超级用户权限运行命令。 - aptitude: 包管理工具,用于安装、更新和删除软件包。 - install: 安装指…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
