我谈《概率论与数理统计》的知识体系

学习《概率论与数理统计》二十多年后,在廖老师的指导下,才厘清了各章之间的关系。首先,这是两个学科综合的一门课程,这一门课程中还有术语冲突的问题。这一门课程一条线两个分支,脉络很清晰。
概率论与统计学
概率论与统计学是数学的两个分支,它们密切相关但有着不同的侧重点和目标。
-
概率论:
概率论是一门研究随机现象及其规律性的数学学科。它处理的是在给定条件下某个事件发生的可能性大小的问题。概率论通过定义样本空间、事件以及概率测度等概念来描述不确定性,并基于这些概念发展出一系列理论工具,如随机变量、分布函数、期望值、方差等。概率论的研究对象可以是离散型或连续型的随机变量,也可以是多维随机变量和随机过程。 -
统计学:
统计学则是利用数据来推断概率模型的参数或进行预测的一门科学。它关注如何收集、整理、分析和解释数据,以从数据中提取有用的信息并作出决策或得出结论。统计学分为描述性统计和推断性统计两大类:前者侧重于总结数据特征(如均值、中位数、标准差等),后者则涉及到对未知总体的估计和假设检验等问题。统计学还涉及实验设计、抽样方法、回归分析等多个方面。
数理统计是统计学的一个分支,它依赖于概率论的理论基础,并结合数学方法来研究如何有效地收集、分析和解释数据。数理统计主要关注的是从样本数据中得出关于总体的结论,以及评估这些结论的可靠性。
知识体系
分支一:从随机现象到样本空间到随机事件再到概率。
从随机事件到随机变量:为了进行定量的数学处理,必须把随机现象的结果数量化,这就是引入随机变量的原因。
分支二:从随机现象到样本空间到随机变量的取值到分布,再到采样到随机样本,根据样本统计推断,估计分布。
概率论与数理统计的教材中缺少采样的部分,就使这条线断了。
随机变量
随机变量的取值是随机变量定义在样本空间上的实值函数。
随机变量既是变量也是函数。
从变量的角度来看,随机变量是指在随机试验或者随机过程中可能取不同数值的一种变量,它的数值受随机因素影响,无法事先确切预知。
从函数的角度来看,随机变量是定义在样本空间(随机试验所有可能结果组成的集合)上的一个实值函数。它将随机试验的所有可能结果(样本点)映射到实数集合上,每一个样本点对应一个实数值。随机变量的本质是对不确定事件结果的一种量化表示,使得原本非数值化的随机现象可以用数学语言来描述。
随机变量结合了变量的不确定性属性与函数的映射特性,它通过函数的方式将随机事件的结果量化,并通过概率论的语言来描述这些结果出现的可能性分布。
随机变量的分布
有了随机变量,然后就可以谈分布了。
定义 定义在样本空间Ω上的实值函数 X = X ( ω ) X=X(ω) X=X(ω)称为随机变量,常用大写字母X, Y, Z等表示随机变量,其取值用小写字母x, y, z等表示。假如一个随机变量仅可能取有限个或可列个值,则称其为离散随机变量。假如一个随机变量的可能取值充满数轴上的一个区间(a, b),则称其为连续随机变量,其中a可以是 − ∞ -\infty −∞,b可以是 + ∞ +\infty +∞。
连续型随机变量用概率密度函数描述分布,离散型随机变量用分布律描述分布。
以后当我们提到一个随机变量 X X X的“概率分布”时,指的是它的分布函数;或者,当 X X X是连续型随机变量时,指的是它的概率密度;当 X X X是离散型随机变量时,指的是它的分布律。
总之,分布描述随机变量取值的概率。
采样与随机样本
有了分布谈采样(抽样),就有了样本。
定义 设 X X X是具有分布函数 F F F的随机变量,若 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X1,X2,⋯,Xn是具有同一分布函数 F F F的、相互独立的随机变量,则称 X 1 , X 2 , ⋯ , X n X_1, X_2,\cdots, X_n X1,X2,⋯,Xn为从分布函数 F F F(或总体 F F F、或总体 X X X)得到的容量为 n n n的简单随机样本,简称样本,它们的观察值 x 1 , x 2 , ⋯ , x n x_1, x_2,\cdots, x_n x1,x2,⋯,xn称为样本值,又称为 X X X的 n n n个独立的观察值。
在统计学中,样本是从总体(Population)中选取的一部分个体或观测值。它用来代表整个总体,并用于估计总体的特征或参数。

统计推断
之后就是统计推断。
样本是进行统计推断的依据。在统计学中,我们通常无法对整个总体进行测量或观察,因此需要从总体中抽取一部分个体组成样本。通过对样本的分析,我们可以对总体的特征进行估计和推断。
统计推断的基本问题可以分为两大类,一类是估计问题,另一类是假设检验问题。
Comments
概率论与数理统计理论性比较强,很抽象,但是这是一个很实用的学科,相比高等代数和数学分析来说与我们更加接近。
然而这门课老师竟然讲成了一门抽象的理论课。凡是只讲怎么代入公式计算,没有解释,没有剖析,不讲整个知识体系以及逻辑关系,那样的概率老师都应该回家卖红薯。
相关文章:

我谈《概率论与数理统计》的知识体系
学习《概率论与数理统计》二十多年后,在廖老师的指导下,才厘清了各章之间的关系。首先,这是两个学科综合的一门课程,这一门课程中还有术语冲突的问题。这一门课程一条线两个分支,脉络很清晰。 概率论与统计学 概率论…...

五、华为 RSTP
RSTP(Rapid Spanning Tree Protocol,快速生成树协议)是 STP 的优化版本,能实现网络拓扑的快速收敛。 一、RSTP 原理 快速收敛机制:RSTP 通过引入边缘端口、P/A(Proposal/Agreement)机制等&…...

基于Java Web的网上房屋租售网站
内容摘要 本毕业设计题目为《基于Java Web的网上房屋租售网站》,是在信息化时代下充分利用互联网对传统房屋租售方式进行创新,在互联网上进行房屋租售突破了传统方式的局限性。对于房屋租售的当事人都提供了极大的便利。本稳针对了实际用户需求…...

Pyside6(PyQT5)中的QTableView与QSqlQueryModel、QSqlTableModel的联合使用
QTableView 是QT的一个强大的表视图部件,可以与模型结合使用以显示和编辑数据。QSqlQueryModel、QSqlTableModel 都是用于与 SQL 数据库交互的模型,将二者与QTableView结合使用可以轻松地展示和编辑数据库的数据。 QSqlQueryModel的简单应用 import sys from PySid…...

git常用命令学习
目录 文章目录 目录第一章 git简介1.Git 与SVN2.Git 工作区、暂存区和版本库 第二章 git常用命令学习1.ssh设置2.设置用户信息3.常用命令设置1.初始化本地仓库init2.克隆clone3.查看状态 git status4.添加add命令5.添加评论6.分支操作1.创建分支2.查看分支3.切换分支4.删除分支…...

【优选算法】7----三数之和
来了来了,他来了,又是学习算法的一天~ 今天的嘉宾是中等难度的算法题----三数之和! ------------------------------------------begin------------------------------------ 题目解析: 哇趣!又是给了一个数组&#…...
分子动力学模拟里的术语:leap-frog蛙跳算法和Velocity-Verlet算法
分子动力学模拟(Molecular Dynamics Simulation,简称MD)是一种基于经典力学原理的计算物理方法,用于模拟原子和分子在给定时间内的运动和相互作用。以下是关于分子动力学模拟的一些核心术语和概念: 定义系统&am…...

2025年数学建模美赛:A题分析(1)Testing Time: The Constant Wear On Stairs
2025年数学建模美赛 A题分析(1)Testing Time: The Constant Wear On Stairs 2025年数学建模美赛 A题分析(2)楼梯磨损分析模型 2025年数学建模美赛 A题分析(3)楼梯使用方向偏好模型 2025年数学建模美赛 A题分…...

利用 SoybeanAdmin 实现前后端分离的企业级管理系统
引言 随着前后端分离架构的普及,越来越多的企业级应用开始采用这种方式来开发。前后端分离不仅提升了开发效率,还让前端和后端开发可以并行进行,减少了相互之间的耦合度。SoybeanAdmin 是一款基于 Spring Boot 和 MyBatis-Plus 的后台管理系…...
996引擎 - 前期准备-配置开发环境
996引擎 - 前期准备 官网搭建服务端、客户端单机搭建 开发环境配置后端开发环境配置环境 前端开发环境配置环境 后端简介前端简介GUILayoutGUIExport 官网 996传奇引擎官网 所有资料从官网首页开始,多探索。 文档: 996M2-服务端Lua 996M2-客户端Lua 搭…...

Tensor 基本操作4 理解 indexing,加减乘除和 broadcasting 运算 | PyTorch 深度学习实战
前一篇文章,Tensor 基本操作3 理解 shape, stride, storage, view,is_contiguous 和 reshape 操作 | PyTorch 深度学习实战 本系列文章 GitHub Repo: https://github.com/hailiang-wang/pytorch-get-started Tensor 基本使用 索引 indexing示例代码 加减…...

【Uniapp-Vue3】request各种不同类型的参数详解
一、参数携带 我们调用该接口的时候需要传入type参数。 第一种 路径名称?参数名1参数值1&参数名2参数值2 第二种 uni.request({ url:"请求路径", data:{ 参数名:参数值 } }) 二、请求方式 常用的有get,post和put 三种,默认是get请求。…...

【Prometheus】Prometheus如何监控Haproxy
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

SSM开发(一)JAVA,javaEE,spring,springmvc,springboot,SSM,SSH等几个概念区别
目录 JAVA 框架 javaEE spring springmvc springboot SSM SSH maven JAVA 一种面向对象、高级编程语言,Python也是高级编程语言;不是框架(框架:一般用于大型复杂需求项目,用于快速开发)具有三大特性,所谓Jav…...

HTML5 常用事件详解
在现代 Web 开发中,用户交互是提升用户体验的关键。HTML5 提供了丰富的事件机制,允许开发者监听用户的操作(如点击、拖动、键盘输入等),并触发相应的逻辑处理。本文将详细介绍 HTML5 中的常用事件,包括鼠标…...

TCP全连接队列
1. 理解 int listen(int sockfd, int backlog) 第二个参数的作用 backlog:表示tcp全连接队列的连接个数1。 如果连接个数等于backlog1,后续连接就会失败,假设tcp连接个数为0,最大连接个数就为1,并且不accept获取连接…...

统计文本文件中单词频率的 Swift 与 Bash 实现详解
网罗开发 (小红书、快手、视频号同名) 大家好,我是 展菲,目前在上市企业从事人工智能项目研发管理工作,平时热衷于分享各种编程领域的软硬技能知识以及前沿技术,包括iOS、前端、Harmony OS、Java、Python等…...
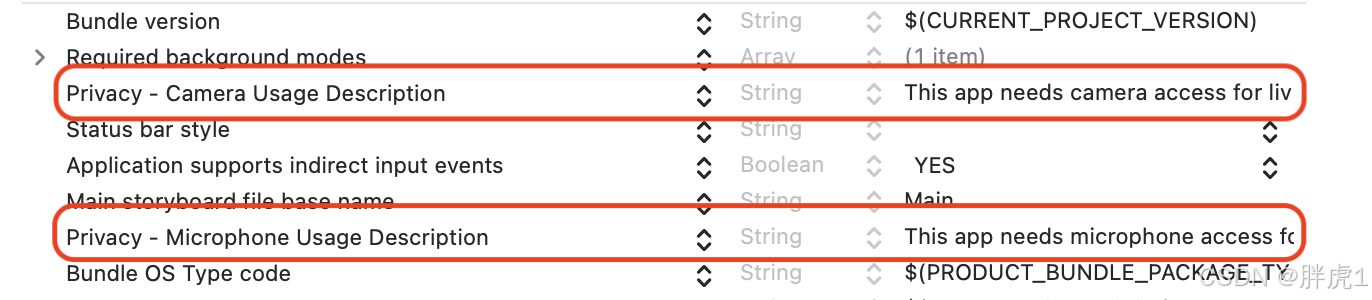
iOS 权限管理:同时请求相机和麦克风权限的最佳实践
引言 在开发视频类应用时,我们常常会遇到需要同时请求相机和麦克风权限的场景。比如,在用户发布视频动态时,相机用于捕捉画面,麦克风用于录制声音;又或者在直播功能中,只有获得这两项权限,用户…...

Excel 实现文本拼接方法
1. 使用 & 运算符 这是最常见和简单的拼接方法。你只需使用 & 来连接多个文本单元格或文本字符串。 示例公式: A1 & B1这个公式会将 A1 和 B1 单元格中的文本合并为一个字符串。 如果你希望在文本之间加入分隔符(如空格、逗号等…...

软考信安27~Windows操作系统安全相关
1、Windows账户与组管理 1.1、用户账户查看 whoami #查看当前登录的用户名称 whoami /all #查看当前系统的用户名和组信息,以及SID whoami /user #查看当前用户的SID net user #查看系统中包含哪些用户 wmic useraccount get name,sid #查看…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
