代码随想录 二叉树 test 2
二叉树的非递归遍历
先序
方法一:
先保存根节点,用来之后找到右子树(利用栈来回溯到根,进而找到右子树)
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列stack<TreeNode*> stk;TreeNode* p = root;while(p || !stk.empty()){if(p != nullptr){ res.push_back(p->val); //访问根节点stk.push(p);p = p->left; //移动到左子树}else{ //如果左子树为空,就需要访问上一个结点的右子树p = stk.top();stk.pop();p = p->right;}}return res;}
};方法二:
不用回溯,利用栈的先进后出性质,先将右子树入栈,再将左子树入栈,实现根左右。
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {if(!root) return {};vector<int> res; //存遍历序列stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* p = stk.top();stk.pop();res.push_back(p->val); //根if(p->right) stk.push(p->right); //将非空的右孩子压栈if(p->left) stk.push(p->left); //将非空的左孩子压栈}return res;}
};方法三:统一迭代法
每次以根节点为处理对象,如果当前遍历的结点非空,则按照右左根顺序,将三个结点都压入栈中,在压入根节点之后继续压入空指针,因此处理顺序与出栈顺序对应。如果为空,则当前该结点需要输出。
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列if(!root) return res;stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* p = stk.top();if(p != nullptr){stk.pop();if(p->right) stk.push(p->right); //右if(p->left) stk.push(p->left); //左stk.push(p); //中stk.push(nullptr); //标记在空结点之下即为要处理的结点}else{stk.pop(); //弹出空结点p = stk.top(); //访问要处理的结点stk.pop(); //弹出已处理好的结点res.push_back(p->val);}}return res;}
};中序
方法一
与先序方法一类似,将访问结点操作放在遍历到当前最左结点之后。
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列stack<TreeNode*> stk;TreeNode* p = root;while(p || !stk.empty()){if(p != nullptr){ stk.push(p);p = p->left; //移动到左子树}else{ //如果左子树为空,就需要访问上一个结点的右子树p = stk.top();stk.pop();res.push_back(p->val); //访问左p = p->right;}}return res;}
};方法二:统一迭代法
只需将先序中的统一迭代法,按照右根左入栈即可。
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列if(!root) return res;stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* p = stk.top();if(p != nullptr){stk.pop();if(p->right) stk.push(p->right); //右stk.push(p); //中stk.push(nullptr); //标记在空结点之下即为要处理的结点if(p->left) stk.push(p->left); //左}else{stk.pop(); //弹出空结点p = stk.top(); //访问要处理的结点stk.pop(); //弹出已处理好的结点res.push_back(p->val);}}return res;}
};后序
方法一
改写先序方法一,由于遍历顺序要求是左右根,因此回溯的情况既可能是遍历完左子树也可能是遍历完右子树。如果是遍历完左子树且有右子树且右子树未被遍历过,则需要继续遍历右子树,如果是遍历完右子树,则此时栈顶元素即为当前最右,需要进行处理,处理完最右结点需要回溯到根,因此需要将当前指针置为空,在下一次循环就可以取出栈顶根。由上可知需要标记结点是否被遍历过,因此需要一个指针r记录上一个遍历过的结点。
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列stack<TreeNode*> stk;TreeNode* p = root;TreeNode* r = nullptr;while(p || !stk.empty()){if(p != nullptr){ stk.push(p);p = p->left; //移动到左子树}else{ //如果左子树为空,就需要检查右子树状态p = stk.top();if(p->right && r != p->right){ //如果有右子树且未被遍历过p = p->right;}else{ //否则应该处理栈顶元素p = stk.top();stk.pop();res.push_back(p->val); //处理栈顶r = p; //标记此结点已被处理p = nullptr;}}}return res;}
};方法二:改写先序方法二+反转
先序方法二颠倒左右子树入栈顺序实现根右左,再进行反转,变成左右根。
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {if(!root) return {};vector<int> res; //存遍历序列stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* p = stk.top();stk.pop();res.push_back(p->val); //根if(p->left) stk.push(p->left); //将非空的左孩子压栈if(p->right) stk.push(p->right); //将非空的右孩子压栈}reverse(res.begin(), res.end()); //反转数组return res;}
};方法三:统一迭代法
按照根右左顺序入栈
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列if(!root) return res;stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* p = stk.top();if(p != nullptr){stk.pop();stk.push(p); //中stk.push(nullptr); //标记在空结点之下即为要处理的结点if(p->right) stk.push(p->right); //右if(p->left) stk.push(p->left); //左}else{stk.pop(); //弹出空结点p = stk.top(); //访问要处理的结点stk.pop(); //弹出已处理好的结点res.push_back(p->val);}}return res;}
};相关文章:

代码随想录 二叉树 test 2
二叉树的非递归遍历 先序 方法一: 先保存根节点,用来之后找到右子树(利用栈来回溯到根,进而找到右子树) class Solution { public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res; //存遍历序列stack<TreeNode*…...

浏览器默认语言与页面访问统计问题二三则
文章目录 前言网站默认语言问题网站访问统计问题Error: Empty components are self-closingError: A space is required before closing bracket 总结 前言 看标题大概能猜到这是一篇杂合体的总结,是这两天处理网站遇到的小问题,怕过段时间再忘了所以总…...

用Python绘制一只懒羊羊
目录 一、准备工作 二、Turtle库简介 三、绘制懒羊羊的步骤 1. 导入Turtle库并设置画布 2. 绘制头部 3. 绘制眼睛 4. 绘制嘴巴 5. 绘制身体 6. 绘制四肢 7. 完成绘制 五、运行代码与结果展示 六、总结 在这个趣味盎然的技术实践中,我们将使用Python和Turtle图形…...

虹科分享 | 汽车NVH小课堂之听音辨故障
随着车主开始关注汽车抖动异响问题,如何根据故障现象快速诊断异响来源,成了汽修人的必修课。 一个比较常用的方法就是靠“听”——“听音辨故障”。那今天,虹科Pico也整理了几个不同类型的异响声音,一起来听听看你能答对几个吧 汽…...

论文速读|SigLIP:Sigmoid Loss for Language Image Pre-Training.ICCV23
论文地址:https://arxiv.org/abs/2303.15343v4 代码地址:https://github.com/google-research/big_vision bib引用: misc{zhai2023sigmoidlosslanguageimage,title{Sigmoid Loss for Language Image Pre-Training}, author{Xiaohua Zhai and…...
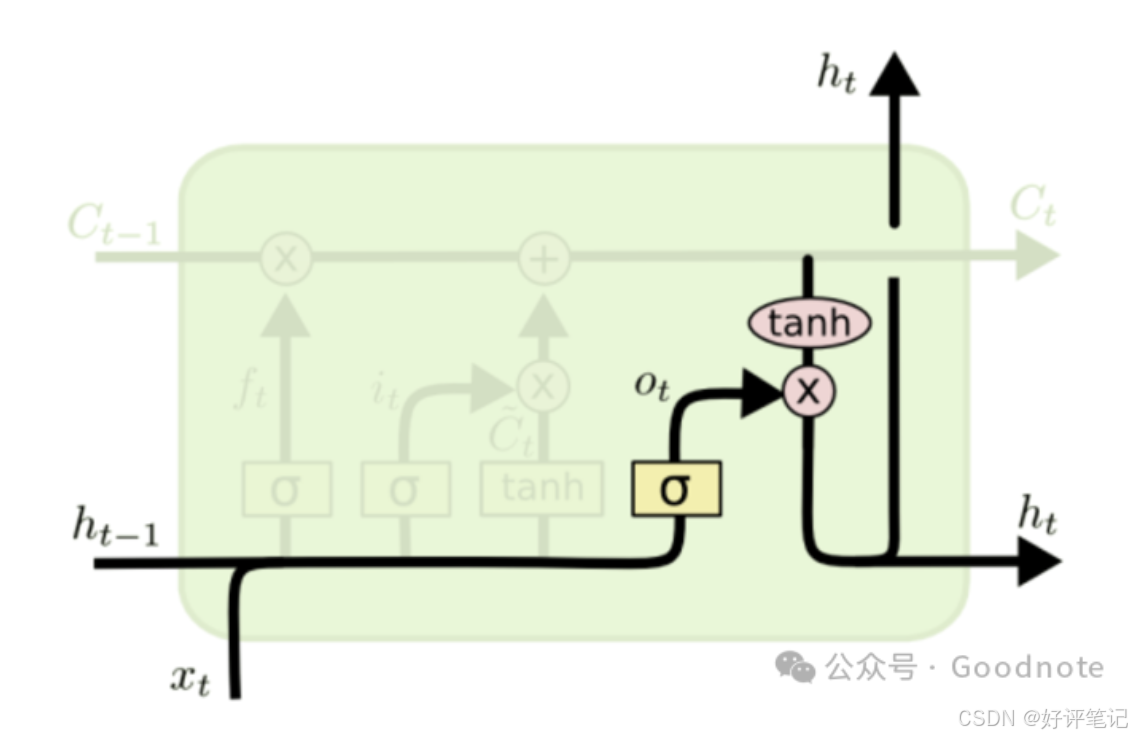
深度学习笔记——循环神经网络之LSTM
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细介绍面试过程中可能遇到的循环神经网络LSTM知识点。 文章目录 文本特征提取的方法1. 基础方法1.1 词袋模型(Bag of Words, BOW)工作…...
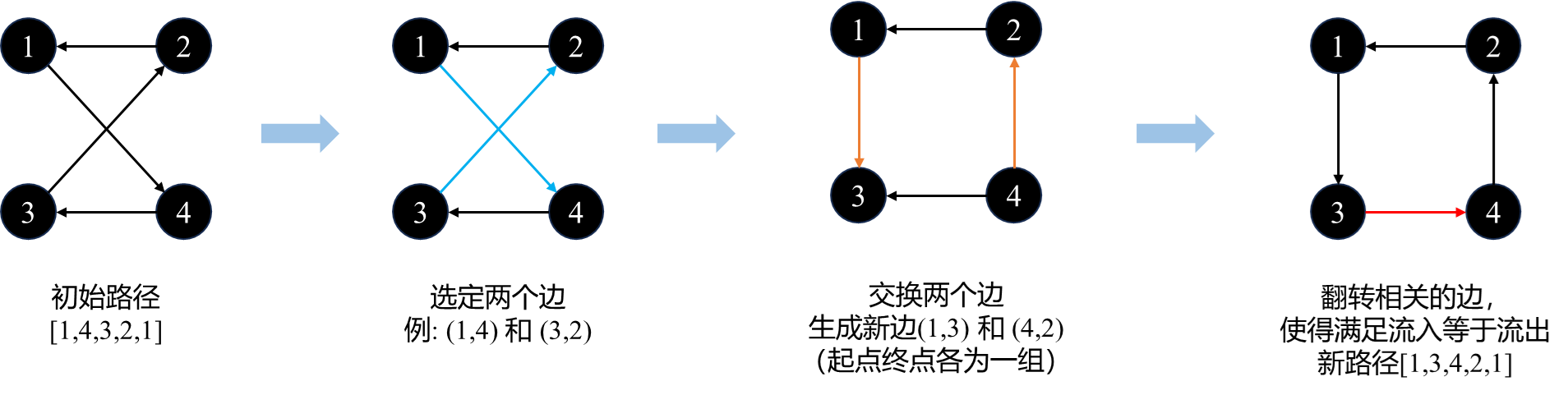
算法整理:2-opt求解旅行商(Python代码)
文章目录 算法思想算法步骤代码1纯函数代码2纯函数数据可视化 算法思想 通过交换边进行寻优。 算法步骤 把初始解作为当前解 通过交换边生成新解 如果新解优于历史最优解,则更新当前解为新解 重复2,3,直到当前解交换了所有的边均不能改…...

状态模式
在软件开发过程中,我们经常会遇到这样的情况:一个对象的行为会随着其内部状态的改变而发生变化。例如,一个手机在不同状态下(开机、关机、静音等)对相同的操作(如来电)会有不同的反应。传统的解…...

RoHS 简介
RoHS(Restriction of Hazardous Substances Directive,限制有害物质指令)是欧盟制定的一项环保法规,旨在限制电气和电子设备中某些有害物质的使用,以减少这些产品对环境和人体健康的危害。 RoHS限制的有害物质及其限量…...

【Vim Masterclass 笔记26】S11L46:Vim 插件的安装、使用与日常管理
文章目录 Section 11:Vim PluginsS11L46 Managing Vim Plugins1 第三方插件管理工具2 安装插件使用的搜索引擎3 Vim 插件的安装方法4 存放 Vim 插件包的路径格式5 示例一:插件 NERDTree 的安装6 示例二:插件 ctrlp.vim 的安装7 示例三&#x…...

深度学习原理与Pytorch实战
深度学习原理与Pytorch实战 第2版 强化学习人工智能神经网络书籍 python动手学深度学习框架书 TransformerBERT图神经网络: 技术讲解 编辑推荐 1.基于PyTorch新版本,涵盖深度学习基础知识和前沿技术,由浅入深,通俗易懂…...

ELK环境搭建
文章目录 1.ElasticSearch安装1.安装的版本选择1.SpringBoot版本:2.4.2 找到依赖的spring-data-elasticsearch的版本2.spring-data-elasticsearch版本:4.1.3 找到依赖的elasticsearch版本3.elasticsearch版本:7.9.3 2.安装1.官方文档2.下载压…...
基于Springboot + vue实现的民俗网
“前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站:人工智能学习网站” 💖学习知识需费心, 📕整理归纳更费神。 🎉源码免费人人喜…...
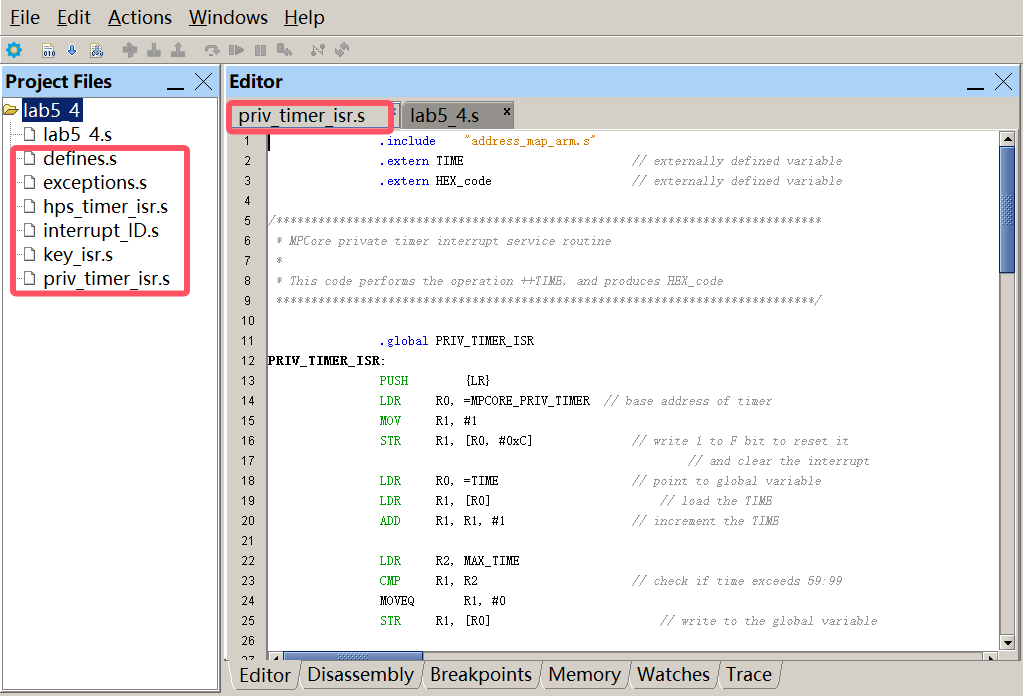
第24篇 基于ARM A9处理器用汇编语言实现中断<六>
Q:怎样设计ARM处理器汇编语言程序使用定时器中断实现实时时钟? A:此前我们曾使用轮询定时器I/O的方式实现实时时钟,而在本实验中将采用定时器中断的方式。新增第三个中断源A9 Private Timer,对该定时器进行配置&#…...
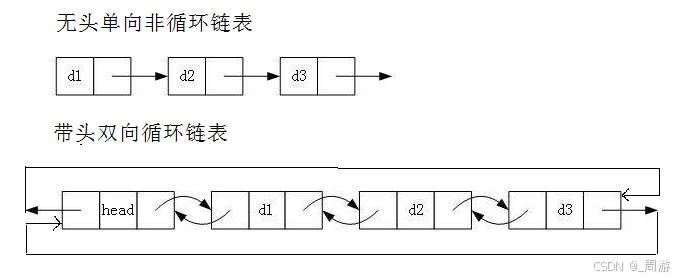
【数据结构】_不带头非循环单向链表
目录 1. 链表的概念及结构 2. 链表的分类 3. 单链表的实现 3.1 SList.h头文件 3.2 SList.c源文件 3.3 Test_SList.c测试文件 关于线性表,已介绍顺序表,详见下文: 【数据结构】_顺序表-CSDN博客 本文介绍链表; 基于顺序表…...

golang 使用双向链表作为container/heap的载体
MyHeap:container/heap的数据载体,需要实现以下方法: Len:堆中数据个数 Less:第i个元素 是否必 第j个元素 值小 Swap:交换第i个元素和 第j个元素 Push:向堆中追加元素 Pop:从堆…...

C#集合操作优化:高效实现批量添加与删除
在C#中,对集合进行批量操作(如批量添加或删除元素)通常涉及使用集合类型提供的方法和特性,以及可能的循环或LINQ查询来高效地处理大量数据。以下是一些常见的方法和技巧: 批量添加元素 使用集合的AddRange方法&#x…...

142.WEB渗透测试-信息收集-小程序、app(13)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:141.WEB渗透测试-信息收集-小程序、app(12) 软件用法,…...

24.日常算法
1. 数组中两元素的最大乘积 题目来源 给你一个整数数组 nums,请你选择数组的两个不同下标 i 和 j,使 (nums[i]-1)*(nums[j]-1) 取得最大值。请你计算并返回该式的最大值。 示例 1: 输入:nums [3,4,5,2] 输出:12 解释…...
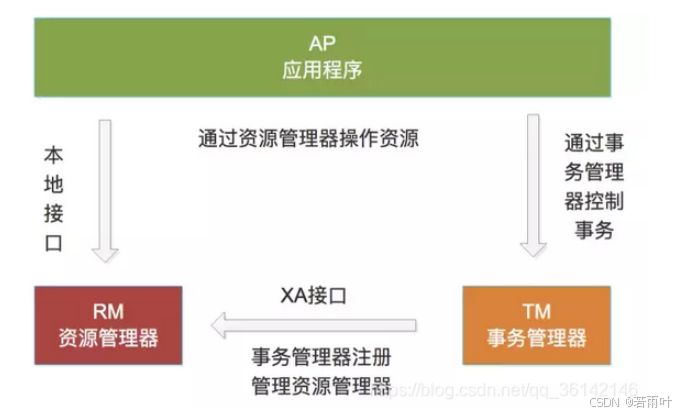
分布式理解
分布式 如何理解分布式 狭义的分布是指,指多台PC在地理位置上分布在不同的地方。 分布式系统 分布式系**统:**多个能独立运行的计算机(称为结点)组成。各个结点利用计算机网络进行信息传递,从而实现共同的“目标或者任…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
