二叉树的深度
- 二叉树深度的定义:
- 二叉树的深度(高度)是指从根节点到最远叶子节点的最长路径上的节点数。例如,一个只有根节点的二叉树,其深度为1;如果根节点有两个子节点,且每个子节点又分别有两个子节点,那么这个二叉树的深度为3。
- 计算二叉树深度的方法:
- 递归方法:
- 递归是解决二叉树问题的常用方法。对于二叉树深度的计算,其递归的思想是:二叉树的深度等于其左子树和右子树深度的最大值加1。
- 以下是使用Python实现的代码:
- 递归方法:
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef max_depth(root):if not root:return 0left_depth = max_depth(root.left)right_depth = max_depth(root.right)return max(left_depth, right_depth)+1# 示例用法
# 创建一个简单的二叉树
root = TreeNode(3)
root.left = TreeNode(9)
root.right = TreeNode(20)
root.right.left = TreeNode(15)
root.right.right = TreeNode(7)
print(max_depth(root))
- 层序遍历方法:
- 层序遍历二叉树可以通过队列来实现。 在遍历过程中,记录遍历的层数,最后一层的层数就是二叉树的深度。
- 以下是使用Python实现的代码:
from collections import dequeclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightdef max_depth(root):if not root:return 0queue = deque([root])depth = 0while queue:level_size = len(queue)for _ in range(level_size):node = queue.popleft()if node.left:queue.append(node.left)if node.right:queue.append(node.right)depth += 1return depth# 示例用法
# 创建一个简单的二叉树
root = TreeNode(3)
root.left = TreeNode(9)
root.right = TreeNode(20)
root.right.left = TreeNode(15)
root.right.right = TreeNode(7)
print(max_depth(root))
- 复杂度分析:
以下是使用其他编程语言(如Java、C++)来计算二叉树深度的示例:
Java实现
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }
}public class BinaryTreeDepth {public static int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return Math.max(leftDepth, rightDepth) + 1;}public static void main(String[] args) {TreeNode root = new TreeNode(3);root.left = new TreeNode(9);root.right = new TreeNode(20);root.right.left = new TreeNode(15);root.right.right = new TreeNode(7);System.out.println(maxDepth(root));}
}
C++实现
#include <iostream>
#include <queue>using namespace std;// 定义二叉树节点结构
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};// 递归方法计算二叉树深度
int maxDepthRecursive(TreeNode* root) {if (root == nullptr) {return 0;}int leftDepth = maxDepthRecursive(root->left);int rightDepth = maxDepthRecursive(root->right);return max(leftDepth, rightDepth) + 1;
}// 层序遍历方法计算二叉树深度
int maxDepthLevelOrder(TreeNode* root) {if (root == nullptr) {return 0;}queue<TreeNode*> q;q.push(root);int depth = 0;while (!q.empty()) {int levelSize = q.size();for (int i = 0; i < levelSize; ++i) {TreeNode* node = q.front();q.pop();if (node->left) {q.push(node->left);}if (node->right) {q.push(node->right);}}depth++;}return depth;
}int main() {TreeNode* root = new TreeNode(3);root->left = new TreeNode(9);root->right = new TreeNode(20);root->right->left = new TreeNode(15);root->right->right = new TreeNode(7);cout << "递归方法计算的深度: " << maxDepthRecursive(root) << endl;cout << "层序遍历方法计算的深度: " << maxDepthLevelOrder(root) << endl;return 0;
}
不同方法的应用场景
- 递归方法:
- 代码简洁明了,逻辑清晰,非常适合处理树结构的问题,因为树本身就是递归定义的。对于简单的二叉树深度计算,递归方法很容易理解和实现。
- 但在处理非常大的二叉树时,由于递归调用会占用栈空间,如果二叉树非常深(特别是在最坏情况下,二叉树是一条链),可能会导致栈溢出问题。
- 层序遍历方法:
- 层序遍历方法直观地按照树的层次来处理节点,在计算深度时更加直接。不需要额外的递归调用栈空间,因此在处理非常大的二叉树时更加稳健,不会出现栈溢出的问题。
- 缺点是代码相对复杂一些,需要使用队列来辅助实现层序遍历,理解和编写的难度稍高。
总结
计算二叉树的深度是二叉树相关算法中的一个基础问题,通过递归和层序遍历这两种常见方法都可以有效地解决。在实际应用中,可以根据二叉树的特点(如大小、结构等)以及具体的需求来选择合适的方法。
相关文章:

二叉树的深度
二叉树深度的定义: 二叉树的深度(高度)是指从根节点到最远叶子节点的最长路径上的节点数。例如,一个只有根节点的二叉树,其深度为1;如果根节点有两个子节点,且每个子节点又分别有两个子节点&…...
)
MySQL命令及用法(精华版)
目录 DDL(数据定义语言) 数据库操作 表操作 DML(数据操作语言) DQL(数据查询语言) 基本查询 条件查询 聚合函数 分组查询 排序查询 分页查询 DCL(数据控制语言) 用户…...

R语言学习笔记之高效数据操作
一、概要 数据操作是R语言的一大优势,用户可以利用基本包或者拓展包在R语言中进行复杂的数据操作,包括排序、更新、分组汇总等。R数据操作包:data.table和tidyfst两个扩展包。 data.table是当前R中处理数据最快的工具,可以实现快…...
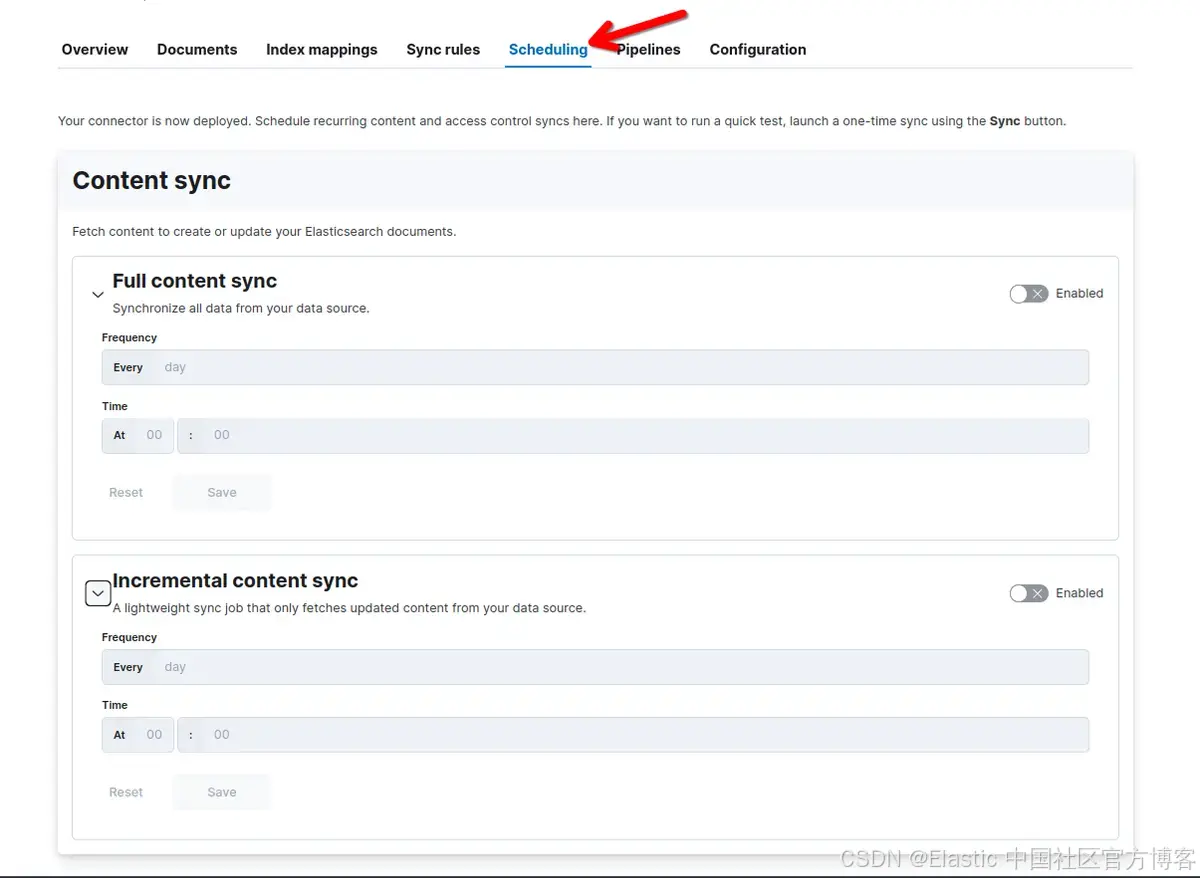
将 OneLake 数据索引到 Elasticsearch - 第二部分
作者:来自 Elastic Gustavo Llermaly 及 Jeffrey Rengifo 本文分为两部分,第二部分介绍如何使用自定义连接器将 OneLake 数据索引并搜索到 Elastic 中。 在本文中,我们将利用第 1 部分中学到的知识来创建 OneLake 自定义 Elasticsearch 连接器…...

Linux——冯 • 诺依曼体系结构
目录 一、冯•诺依曼体系结构原理二、内存提高冯•诺依曼体系结构效率的方法三、当用QQ和朋友聊天时数据的流动过程四、关于冯诺依曼五、总结 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系 流程&#…...

Java进阶(一)
目录 一.Java注解 什么是注解? 内置注解 元注解 二.对象克隆 什么是对象克隆? 为什么用到对象克隆 三.浅克隆深克隆 一.Java注解 什么是注解? java中注解(Annotation)又称java标注,是一种特殊的注释。 可以添加在包,类&…...

appium自动化环境搭建
一、appium介绍 appium介绍 appium是一个开源工具、支持跨平台、用于自动化ios、安卓手机和windows桌面平台上面的原生、移动web和混合应用,支持多种编程语言(python,java,Ruby,Javascript、PHP等) 原生应用和混合应用…...

Qt 5.14.2 学习记录 —— 이십 QFile和多线程
文章目录 1、QFile1、打开2、读写3、关闭4、程序5、其它功能 2、多线程1、演示2、锁 3、条件变量和信号量 1、QFile Qt有自己的一套文件体系,不过Qt也可以使用C,C,Linux的文件操作。使用Qt的文件体系和Qt自己的一些类型更好配合。 管理写入读…...
積分方程與簡單的泛函分析7.希爾伯特-施密特定理
1)def函數叫作"由核生成的(有源的)" 定义: 设 是定义在区域上的核函数。 对于函数,若存在函数使得, 则称函数是“由核生成的(有源的)”。 这里的直观理解是: 函数的“来源”可以通过核函数 与另一个函数的积分运算得到。 在积分方程理论中,这种表述常…...

使用vitepress搭建自己的博客项目
一、介绍can-vitepress-blog 什么是CAN BLOG CAN BLOG是基于vitepress二开的个人博客系统,他能够方便使用者快速构建自己的博客文章,无需繁琐的配置和复杂的代码编写。 CAN BLOG以antdv为UI设计基础,简洁大方,界面友好…...

开始步入达梦中级dba
分析内存使用需要的方法之一 disql /nolog conn sysdba/sysdbaselect value from v$parameter where nameMEMORY_LEAK_CHECK; SP_SET_PARA_VALUE(0,MEMORY_LEAK_CHECK,1); select * from V$MEM_REGINFO; select * from V$MEM_HEAP;...

如何在docker中的mysql容器内执行命令与执行SQL文件
通过 docker ps -a 查询当前运行的容器,找到想执行命令的容器名称。 docker ps -a若想执行sql文件,则将sql文件放入当前文件夹下后将项目内的 SQL 文件拷贝到 mysql 容器内部的 root下。 sudo docker cp /root/enterprise.sql mysql:/root/然后进入 my…...

S4 HANA更改Tax base Amount的字段控制
本文主要介绍在S4 HANA OP中Tax base Amount的字段控制相关设置。具体请参照如下内容: 1. 更改Tax base Amount的字段控制 以上配置用于控制FB60/FB65/FB70/FB75/MIRO的页签“Tax”界面是否可以修改“Tax base Amount”, 如果勾选Change 表示可以修改T…...

Linux权限有关
文章目录 一、添加普通用户二、Xshell下命令行的知识三、 Linux和Windows操作系统四、再探指令和Linux权限五、用户相关用户切换: 今天我们学习与Linux有关的权限等内容,以及一些零碎知识帮助我们理解Linux的系统和Xshell的原理。 本篇是在Xshell环境下执行的。 一…...

【github 使用相关】提交pr和commit message Conventional Commits 规范 代码提交的描述该写什么?
目录 Git 提交信息格式格式描述Subject(标题)Body(正文) 规范的标签(Tag)示例 CG Git 提交信息格式 格式描述 一般开源项目代码库根目录都会有一个 CONTRIBUTING.md 或者其他类似名字的文档来介绍如何开始…...

Docker—搭建Harbor和阿里云私有仓库
Harbor概述 Harbor是一个开源的企业级Docker Registry管理项目,由VMware公司开发。它的主要用途是帮助用户迅速搭建一个企业级的Docker Registry服务,提供比Docker官方公共镜像仓库更为丰富和安全的功能,特别适合企业环境使用。12 Harb…...

Maven的下载安装配置
maven的下载安装配置 maven是什么 Maven 是一个用于 Java 平台的 自动化构建工具,由 Apache 组织提供。它不仅可以用作包管理,还支持项目的开发、打包、测试及部署等一系列行为 Maven的核心功能 项目构建生命周期管理:Maven定义了项目构建…...

Rust:高性能与安全并行的编程语言
引言 在现代编程世界里,开发者面临的最大挑战之一就是如何平衡性能与安全性。在许多情况下,C/C这样的系统级编程语言虽然性能强大,但其内存管理的复杂性导致了各种安全漏洞。为了解决这些问题,Rust 作为一种新的系统级编程语言进入…...
函数详解(OK))
matlab的cat()函数详解(OK)
cat函数的功能是 连接数组 功能: 按指定的维度连接多个向量 结构: C cat(dim, A, B) 按dim指定的维度连接向量A和BC cat(dim, A1, A2, A3,A4, …) 按dim指定的维度连接多个向量A1, A2,A3,A4…C cat(dim, A{:}) 将包含向量的cell或结构数组联合为一…...

将个人微信中的时间改成标准的日期时间格式
list1["10:05","上午 10:07","下午 2:07","晚上 8:07","昨天 16:07","星期天 19:27","星期二 19:27","星期四 14:27","2025年1月10日 17:43"]from datetime import datetime, time…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
