PAT甲级-1024 Palindromic Number
题目


题目大意
一个非回文数,加上它的翻转数所得的和,进行k次,有可能会得到一个回文数。给出一个数n,限制相加次数为k次,如果小于k次就得到回文数,那么输出该回文数和相加的次数;如果进行k次还没有得到回文数,那么输出最后的结果和k值。
思路
10的10次方,按照最坏情况考虑,乘以100,为10的20次方,超过了long long的范围,所以是大数加法题目。要用字符串来表示数字。由于是加法运算,不管哪两个数相加都最多进1位,因此可以用isadd来表示是否需要进位。注意计算首位加法,如果进位,就跳出了for循环,所以要再循环外放一个isadd的if语句,如果进位,res再加‘1’。
代码
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;int main(){string s;int k;cin >> s >> k;for (int i = 0; i < k; i++){string s2 = s;reverse(s2.begin(), s2.end());if (s == s2){cout << s << endl;cout << i << endl;return 0;}string res = "";bool isadd = false;for (int i = (int)s.size() - 1; i >= 0; i--){if (isadd){res += ((s[i] - '0') + (s2[i] - '0') + 1) % 10 + '0'; // 先加1,后取余if ((s[i] - '0') + (s2[i] - '0') + 1 >= 10){isadd = true;}else{isadd = false;}}else{res += ((s[i] - '0') + (s2[i] - '0')) % 10 + '0';if ((s[i] - '0') + (s2[i] - '0') >= 10){isadd = true;}else{isadd = false;}}}if (isadd) res += '1';reverse(res.begin(), res.end());s = res;}cout << s << endl;cout << k << endl;return 0;
}相关文章:

PAT甲级-1024 Palindromic Number
题目 题目大意 一个非回文数,加上它的翻转数所得的和,进行k次,有可能会得到一个回文数。给出一个数n,限制相加次数为k次,如果小于k次就得到回文数,那么输出该回文数和相加的次数;如果进行k次还…...

FS8405 Release FS0B
复位场景:FS8405正常工作后,RSTB后期产生拉低复位信号。 1 故障与PGOOD、RSTB和FS0B引脚的联系 FS8405出现故障时,会对PGOOD、RSTB和FS0B引脚产生不同的影响,具体影响如下: 橙色标记,反应是不可配置的。…...

IGBT的损耗计算的学习【2025/1/24】
可以通过示波器实测IGBT电压电流波形,然后通过示波器的math功能将电压电流波形乘积后积分求损耗。 软开管:给了导通信号,但是电流并没有从此IGBT流过 IGBT(绝缘栅双极晶体管)的损耗主要分为 导通损耗 和 开关损耗 两部…...

Unity|小游戏复刻|见缝插针1(C#)
准备 创建Scenes场景,Scripts脚本,Prefabs预制体文件夹 修改背景颜色 选中Main Camera 找到背景 选择颜色,一种白中透黄的颜色 创建小球 将文件夹里的Circle拖入层级里 选中Circle,位置为左右居中,偏上&…...

No.1|Godot|俄罗斯方块复刻|棋盘和初始方块的设置
删掉基础图标新建assets、scenes、scripts文件夹 俄罗斯方块的每种方块都是由四个小方块组成的,很适合放在网格地图中 比如网格地图是宽10列,高20行 要实现网格的对齐和下落 Node2D节点 新建一个Node2D 添加2个TileMapLayer 一个命名为Board&…...

SSM框架探秘:Spring 整合 SpringMVC 框架
搭建和测试 SpringMVC 的开发环境: web.xml 元素顺序: 在 web.xml 中配置 DisPatcherServlet 前端控制器: <!-- 配置前端控制器 --> <servlet><servlet-name>dispatcherServlet</servlet-name><servlet-class>…...

2025.1.20——二、buuctf BUU UPLOAD COURSE 1 1 文件上传
题目来源:buuctf BUU UPLOAD COURSE 1 1 目录 一、打开靶机,查看信息 二、解题思路 step 1:上传一句话木马.php文件康康回显 step 2:蚁剑连接 三、小结 一、打开靶机,查看信息 这里提示到了文件会被上传到./uplo…...

【架构面试】三、高可用高性能架构设计
高可用高性能架构设计 面试要点引入:架构原理、分布式技术等是面试必考领域,高可用高性能需求考察频繁。面试常通过询问系统架构设计来考察能力,讲解架构设计过程就是证明系统高可用的过程,其中涉及SLA指标。SLA指标详解 定义与衡…...

11.渲染管线——光栅化阶段
光栅化阶段是渲染管线中的一个关键步骤,负责将3D模型转换成屏幕上的2D像素。用通俗易懂的方式来解释: 通俗解释:光栅化就像把3D模型“投影”到2D屏幕上 想象你是一个画家,正在把3D场景画到2D画布上: 3D模型到2D屏幕的…...

【数据分享】1929-2024年全球站点的逐月平均能见度(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标!说到气象数据,最详细的气象数据是具体到气象监测站点的数据! 有关气象指标的监测站点数据,之前我们分享过1929-2024年全球气象站点…...

二叉树的深度
二叉树深度的定义: 二叉树的深度(高度)是指从根节点到最远叶子节点的最长路径上的节点数。例如,一个只有根节点的二叉树,其深度为1;如果根节点有两个子节点,且每个子节点又分别有两个子节点&…...
)
MySQL命令及用法(精华版)
目录 DDL(数据定义语言) 数据库操作 表操作 DML(数据操作语言) DQL(数据查询语言) 基本查询 条件查询 聚合函数 分组查询 排序查询 分页查询 DCL(数据控制语言) 用户…...

R语言学习笔记之高效数据操作
一、概要 数据操作是R语言的一大优势,用户可以利用基本包或者拓展包在R语言中进行复杂的数据操作,包括排序、更新、分组汇总等。R数据操作包:data.table和tidyfst两个扩展包。 data.table是当前R中处理数据最快的工具,可以实现快…...
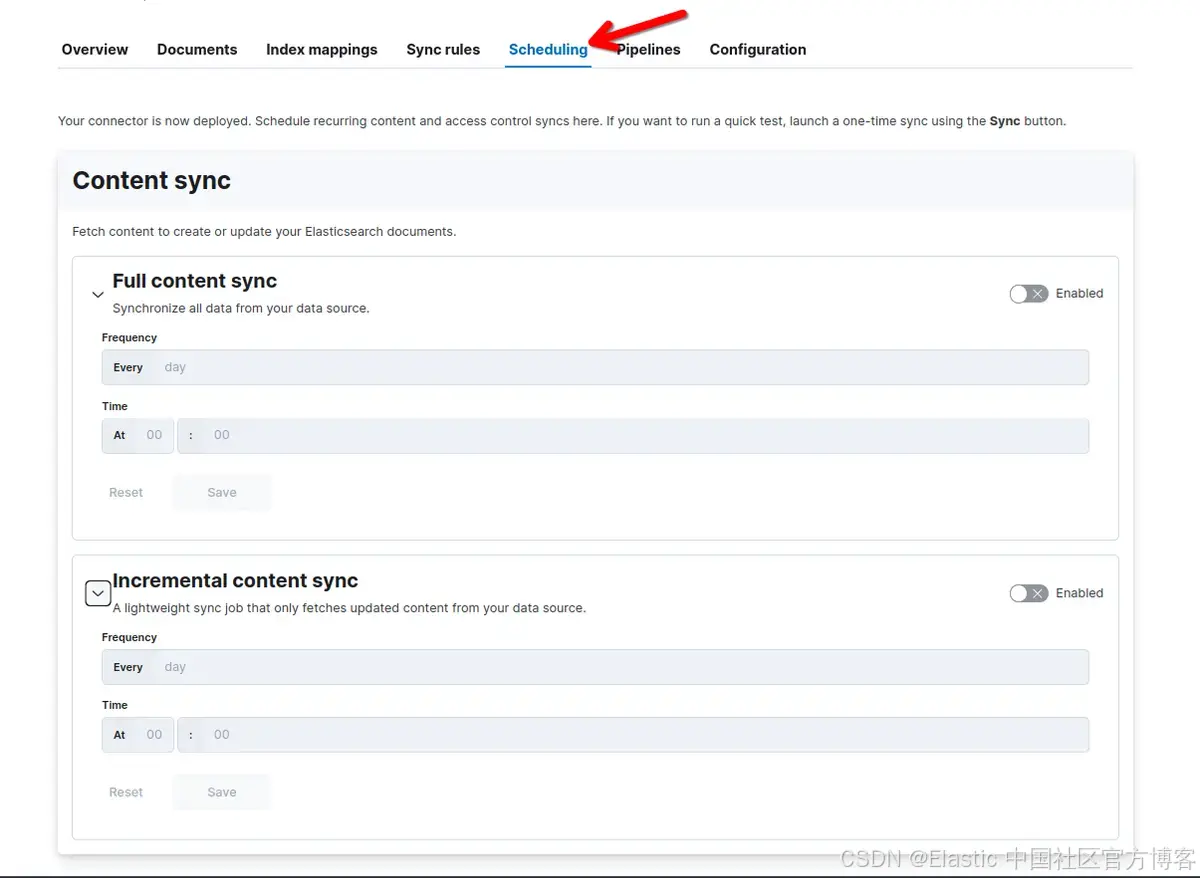
将 OneLake 数据索引到 Elasticsearch - 第二部分
作者:来自 Elastic Gustavo Llermaly 及 Jeffrey Rengifo 本文分为两部分,第二部分介绍如何使用自定义连接器将 OneLake 数据索引并搜索到 Elastic 中。 在本文中,我们将利用第 1 部分中学到的知识来创建 OneLake 自定义 Elasticsearch 连接器…...

Linux——冯 • 诺依曼体系结构
目录 一、冯•诺依曼体系结构原理二、内存提高冯•诺依曼体系结构效率的方法三、当用QQ和朋友聊天时数据的流动过程四、关于冯诺依曼五、总结 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系 流程&#…...

Java进阶(一)
目录 一.Java注解 什么是注解? 内置注解 元注解 二.对象克隆 什么是对象克隆? 为什么用到对象克隆 三.浅克隆深克隆 一.Java注解 什么是注解? java中注解(Annotation)又称java标注,是一种特殊的注释。 可以添加在包,类&…...

appium自动化环境搭建
一、appium介绍 appium介绍 appium是一个开源工具、支持跨平台、用于自动化ios、安卓手机和windows桌面平台上面的原生、移动web和混合应用,支持多种编程语言(python,java,Ruby,Javascript、PHP等) 原生应用和混合应用…...

Qt 5.14.2 学习记录 —— 이십 QFile和多线程
文章目录 1、QFile1、打开2、读写3、关闭4、程序5、其它功能 2、多线程1、演示2、锁 3、条件变量和信号量 1、QFile Qt有自己的一套文件体系,不过Qt也可以使用C,C,Linux的文件操作。使用Qt的文件体系和Qt自己的一些类型更好配合。 管理写入读…...
積分方程與簡單的泛函分析7.希爾伯特-施密特定理
1)def函數叫作"由核生成的(有源的)" 定义: 设 是定义在区域上的核函数。 对于函数,若存在函数使得, 则称函数是“由核生成的(有源的)”。 这里的直观理解是: 函数的“来源”可以通过核函数 与另一个函数的积分运算得到。 在积分方程理论中,这种表述常…...

使用vitepress搭建自己的博客项目
一、介绍can-vitepress-blog 什么是CAN BLOG CAN BLOG是基于vitepress二开的个人博客系统,他能够方便使用者快速构建自己的博客文章,无需繁琐的配置和复杂的代码编写。 CAN BLOG以antdv为UI设计基础,简洁大方,界面友好…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
