高并发问题的多维度解决之道
高并发问题在当今的数字世界里是一个备受关注的挑战。它在系统性能、用户行为以及数据处理等多方面都会引发一系列的问题。例如,可能会导致系统出现性能瓶颈,使得响应出现延迟,进而极大地影响用户体验。
从硬件维度来看,有不少解决高并发问题的策略。对于单体应用可以进行垂直扩容,这意味着要提升 CPU 的运算能力、增加内存、优化磁盘存储以及对网卡进行升级等操作。这些硬件方面的改进就像是给系统的运行搭建了更坚实的基础,能够在一定程度上应对高并发带来的压力。
在流量相关方面,缓存策略起着重要的作用。不同类型的缓存都为解决高并发问题贡献着力量。像浏览器缓存能够在用户端就对一些经常访问的数据进行存储,减少对服务器的重复请求。Nginx 缓存和 CDN 缓存则在网络传输过程中发挥作用,加速数据的传递。而应用缓存是在应用内部对数据进行缓存,提高数据的读取效率。
应用架构层面也需要积极应对高并发。微服务架构和事件驱动架构等都是有效的优化策略。微服务架构将一个大型的应用拆分成多个小型的、独立的服务,每个服务可以独立部署和扩展,这样在面对高并发时能够更灵活地进行资源分配。事件驱动架构则是基于事件来驱动业务逻辑的流转,提高系统的响应速度和处理能力。
代码优化也是提升并发性能的关键。例如采用无锁编程可以避免多线程竞争锁带来的性能损耗。使用线程池可以有效地管理线程资源,提高线程的复用率。异步处理则能让程序在等待某些操作完成的同时可以继续执行其他任务,提高整体的运行效率。
数据库设计优化同样不容忽视。读写分离可以将读操作和写操作分开处理,减轻数据库的负担。索引优化能够加快数据的查询速度,而分库分表则是应对大规模数据存储和高并发访问的有效手段,让数据的管理和查询更加高效。通过这些多维度的策略,可以较为全面地解决高并发问题,保障系统在高并发场景下的稳定运行。

相关文章:

高并发问题的多维度解决之道
…...

Ubuntu环境 nginx 源码 编译安装
ubuntu 终端 使用 wget 下载源码 sudo wget http://nginx.org/download/nginx-1.24.0.tar.gz解压刚下载的源码压缩包 nginx-1.24.0.tar.gz sudo tar -zxvf nginx-1.24.0.tar.gz 解压完成 产生 nginx-1.24.0 目录 进入该目录 cd ./nginx-1.24.0 目录下有一个可执行文件 con…...

K8S中的数据存储之基本存储
基本存储类型 EmptyDir 描述:当 Pod 被调度到节点上时,Kubernetes 会为 Pod 创建一个空目录,所有在该 Pod 中的容器都可以访问这个目录。特点: 生命周期与 Pod 绑定,Pod 删除时,数据也会丢失。适用于临时…...

编码器和扩散模型
目录 摘要abstract1.自动编码器2.变分编码器(VAE)3.论文阅读3.1 介绍3.2 方法3.3 结论 4.总结参考文献 摘要 本周学习了自动编码器(AE)和变分自动编码器(VAE)的基本原理与实现,分析其在数据降维…...

PAT甲级-1024 Palindromic Number
题目 题目大意 一个非回文数,加上它的翻转数所得的和,进行k次,有可能会得到一个回文数。给出一个数n,限制相加次数为k次,如果小于k次就得到回文数,那么输出该回文数和相加的次数;如果进行k次还…...

FS8405 Release FS0B
复位场景:FS8405正常工作后,RSTB后期产生拉低复位信号。 1 故障与PGOOD、RSTB和FS0B引脚的联系 FS8405出现故障时,会对PGOOD、RSTB和FS0B引脚产生不同的影响,具体影响如下: 橙色标记,反应是不可配置的。…...

IGBT的损耗计算的学习【2025/1/24】
可以通过示波器实测IGBT电压电流波形,然后通过示波器的math功能将电压电流波形乘积后积分求损耗。 软开管:给了导通信号,但是电流并没有从此IGBT流过 IGBT(绝缘栅双极晶体管)的损耗主要分为 导通损耗 和 开关损耗 两部…...

Unity|小游戏复刻|见缝插针1(C#)
准备 创建Scenes场景,Scripts脚本,Prefabs预制体文件夹 修改背景颜色 选中Main Camera 找到背景 选择颜色,一种白中透黄的颜色 创建小球 将文件夹里的Circle拖入层级里 选中Circle,位置为左右居中,偏上&…...

No.1|Godot|俄罗斯方块复刻|棋盘和初始方块的设置
删掉基础图标新建assets、scenes、scripts文件夹 俄罗斯方块的每种方块都是由四个小方块组成的,很适合放在网格地图中 比如网格地图是宽10列,高20行 要实现网格的对齐和下落 Node2D节点 新建一个Node2D 添加2个TileMapLayer 一个命名为Board&…...

SSM框架探秘:Spring 整合 SpringMVC 框架
搭建和测试 SpringMVC 的开发环境: web.xml 元素顺序: 在 web.xml 中配置 DisPatcherServlet 前端控制器: <!-- 配置前端控制器 --> <servlet><servlet-name>dispatcherServlet</servlet-name><servlet-class>…...

2025.1.20——二、buuctf BUU UPLOAD COURSE 1 1 文件上传
题目来源:buuctf BUU UPLOAD COURSE 1 1 目录 一、打开靶机,查看信息 二、解题思路 step 1:上传一句话木马.php文件康康回显 step 2:蚁剑连接 三、小结 一、打开靶机,查看信息 这里提示到了文件会被上传到./uplo…...

【架构面试】三、高可用高性能架构设计
高可用高性能架构设计 面试要点引入:架构原理、分布式技术等是面试必考领域,高可用高性能需求考察频繁。面试常通过询问系统架构设计来考察能力,讲解架构设计过程就是证明系统高可用的过程,其中涉及SLA指标。SLA指标详解 定义与衡…...

11.渲染管线——光栅化阶段
光栅化阶段是渲染管线中的一个关键步骤,负责将3D模型转换成屏幕上的2D像素。用通俗易懂的方式来解释: 通俗解释:光栅化就像把3D模型“投影”到2D屏幕上 想象你是一个画家,正在把3D场景画到2D画布上: 3D模型到2D屏幕的…...

【数据分享】1929-2024年全球站点的逐月平均能见度(Shp\Excel\免费获取)
气象数据是在各项研究中都经常使用的数据,气象指标包括气温、风速、降水、湿度等指标!说到气象数据,最详细的气象数据是具体到气象监测站点的数据! 有关气象指标的监测站点数据,之前我们分享过1929-2024年全球气象站点…...

二叉树的深度
二叉树深度的定义: 二叉树的深度(高度)是指从根节点到最远叶子节点的最长路径上的节点数。例如,一个只有根节点的二叉树,其深度为1;如果根节点有两个子节点,且每个子节点又分别有两个子节点&…...
)
MySQL命令及用法(精华版)
目录 DDL(数据定义语言) 数据库操作 表操作 DML(数据操作语言) DQL(数据查询语言) 基本查询 条件查询 聚合函数 分组查询 排序查询 分页查询 DCL(数据控制语言) 用户…...

R语言学习笔记之高效数据操作
一、概要 数据操作是R语言的一大优势,用户可以利用基本包或者拓展包在R语言中进行复杂的数据操作,包括排序、更新、分组汇总等。R数据操作包:data.table和tidyfst两个扩展包。 data.table是当前R中处理数据最快的工具,可以实现快…...
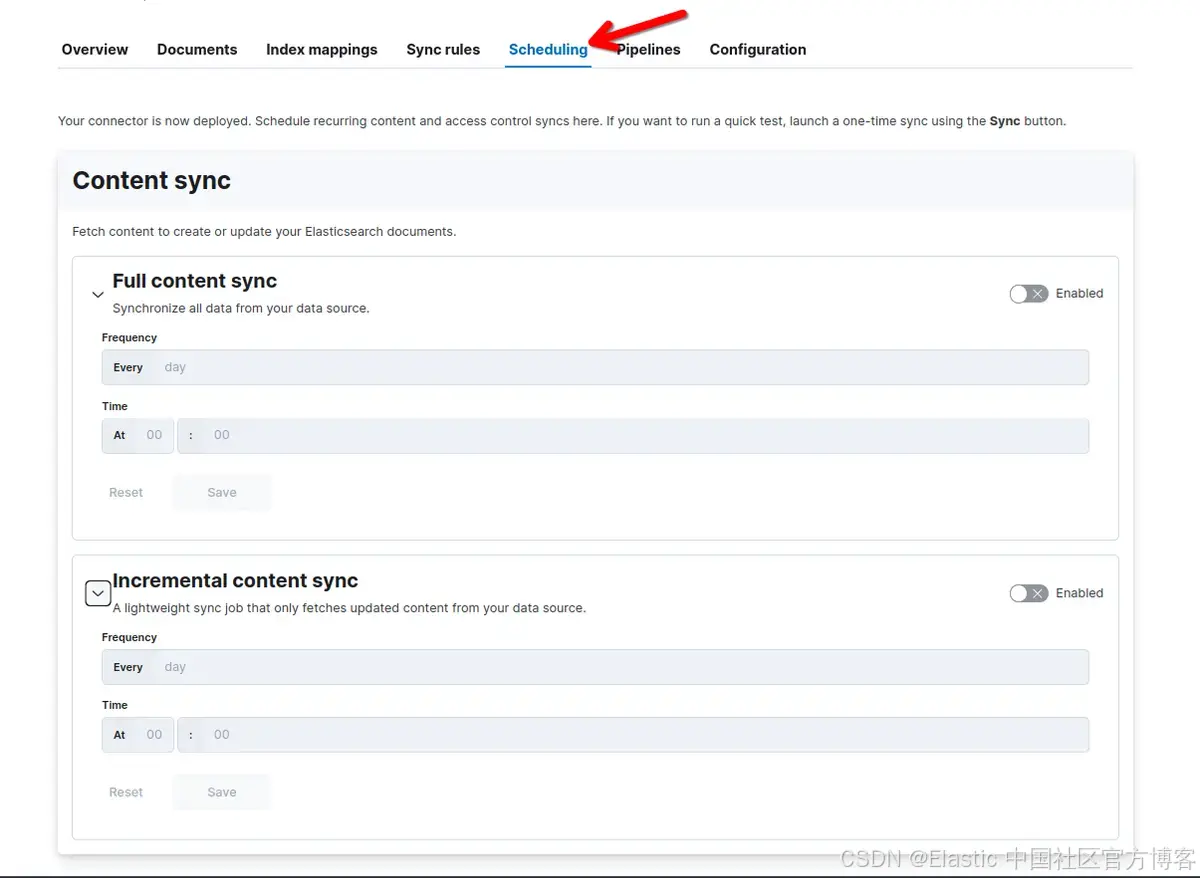
将 OneLake 数据索引到 Elasticsearch - 第二部分
作者:来自 Elastic Gustavo Llermaly 及 Jeffrey Rengifo 本文分为两部分,第二部分介绍如何使用自定义连接器将 OneLake 数据索引并搜索到 Elastic 中。 在本文中,我们将利用第 1 部分中学到的知识来创建 OneLake 自定义 Elasticsearch 连接器…...

Linux——冯 • 诺依曼体系结构
目录 一、冯•诺依曼体系结构原理二、内存提高冯•诺依曼体系结构效率的方法三、当用QQ和朋友聊天时数据的流动过程四、关于冯诺依曼五、总结 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系 流程&#…...

Java进阶(一)
目录 一.Java注解 什么是注解? 内置注解 元注解 二.对象克隆 什么是对象克隆? 为什么用到对象克隆 三.浅克隆深克隆 一.Java注解 什么是注解? java中注解(Annotation)又称java标注,是一种特殊的注释。 可以添加在包,类&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
