当前位置： 首页 > news >正文

three.js+WebGL踩坑经验合集(4.2):为什么不在可视范围内的3D点投影到2D的结果这么不可靠

news 2026/2/10 1:51:42

上一篇，笔者留下了一个问题，three.js内置的THREE.Vector3.project方法算出来的结果对于超出屏幕可见范围的点来说错得相当离谱。

three.js+WebGL踩坑经验合集(4.1):THREE.Line2的射线检测问题（注意本篇说的是Line2，同样也不是阈值方面的问题）-CSDN博客

从代码上看，project方法和常规shader的实现原理并无太大差异，但是为什么错得这么离谱的算法被使用了这么多年都没人去管的呢？

原因很简单，不管怎么错，它都已经出界，不可见了，所以结果的正确与否对于显示来说并不重要。

我们回顾一下上一篇错得很离谱的那个数值，它的xyz都不在0~1的范围内。

但要是想拿它来进行计算的话就完犊子了。就拿上一篇的线来说，假设有且只有一个端点出界，一个点在(0.5,0.1)，另一个点在(-1.2, -1.3)，按照预期，连线向量应该为(1.7, 1.4)，但如果反了，变成(1.2, 1.3)，那连线向量就会被误算成(-0.7, -1.2)，导致后续的结果全部不正确。THREE.Line2射线检测的bug就是这样子来的了。

所以现在我们就来探讨下project方法算不正确的原因。

Vector3的project方法实现代码如下：

project(camera) {return this.applyMatrix4(camera.matrixWorldInverse).applyMatrix4(camera.projectionMatrix);
}

然后我们再来研读下applyMatrix4的代码

applyMatrix4(m) {const x = this.x, y = this.y, z = this.z;const e = m.elements;const w = 1 / (e[3] * x + e[7] * y + e[11] * z + e[15]);this.x = (e[0] * x + e[4] * y + e[8] * z + e[12]) * w;this.y = (e[1] * x + e[5] * y + e[9] * z + e[13]) * w;this.z = (e[2] * x + e[6] * y + e[10] * z + e[14]) * w;return this;}

大体上，它是拿矩阵m跟3D点进行矩阵乘法运算，但是它还多了一个步骤，就是在xyz以外还算了一个w值，并且把w值分别乘到xyz上。

这一步是个什么原理呢？

透视成像近大远小的特性，在数学上大致为反比例的关系。不严谨的说法，同一个物体，我们肉眼所见的大小（s）跟物到我们的距离（z）成反比，即s=1/z。

z在分母，已经无法用矩阵的线性运算进行表达。为了让开发者在处理3D变换的过程中尽可能只跟矩阵打交道，GPU渲染底层在xyz的基础上新增一个w变量，用于处理透视变换，然后称(x, y, z, w)这样的坐标为齐次坐标，最终呈现到屏幕上的，是(x/w, y/w, z/w)这样的值。

可见，THREE.js的Vector3.applyMatrix4中的w跟齐次坐标中的w互为倒数。

笔者不打算给大家探讨投影矩阵的推导过程，网上文章一抓一大把。笔者本人也没啥特别的想法，这里随便给大家搜个两篇：

透视投影矩阵推导

透视投影过程中z值为什么要映射到[0,1]?


笔者只打算给大家列个大纲，说明一下GPU渲染的一些数据结构和工作流程

1 大多数时候，3D点基础变换的计算都基于矩阵乘法。

2 3D点按道理是应该跟3*3矩阵相乘，但是平移是典型的1*3矩阵相加，为了统一，这两种变换合并为1*4和4*4矩阵相乘。并且扩充的行填充单位矩阵的数值[0,0,0,1]，1*4矩阵的最后一列填1

至于为什么合并后会从3*3变成4*4，笔者以前有写过2D矩阵的文章，那里展示了从2*2变成3*3的过程，3*3到4*4可类推。

【原创】《矩阵的史诗级玩法》连载五：45度地图砖块所蕴含的矩阵基础知识（下）_45度地图深度排序-CSDN博客

3 既然合并过程中，点的坐标新增了个1，那么GPU渲染底层就把它拿过来做透视变换了，并且赋予变量w。

4 3D点为齐次坐标(x, y, z, w)，物体自身的变换Model，相机变换都各自有一个矩阵View，投影到屏幕/画布的NDC坐标系Projection会先后作用于该坐标上得到最终结果(x/w, y/w, z/w)，3个矩阵合并称为MVP矩阵。

5 齐次坐标的w值初始为1，前两个矩阵不会修改w，之后P矩阵会修改w从而产生透视效果。

这个大纲还是有点啰嗦了，下面再列一下透视投影矩阵的关键点。

1 w跟z通常成正比，可能是w=z或者w=-z。

2 最终呈现的结果变量，w在分母中。因此，如果w的绝对值很小，甚至等于0，那么这些位置的坐标绝对值将会非常地大，甚至是无穷大。

这么一顿操作之后我们发现，问题点似乎就出现在w上。视锥体的边缘会不会正是w=0的边界？

下面我们不妨就以此为切入点，去看看project方法在视锥体边缘的表现。

既然GPU渲染使用的是齐次坐标，那么three.js也会配套定义了对应的类，Vector4。我们用它来研究将会更加方便。不过Vector4只有applyMatrix4方法，没有project，我们照着Vector3的抄一个。

这里我们单独用一个简单点的相机来测试（顺带加上Vector4的project方法）：

<!DOCTYPE html>
<html>
<head><meta charset="UTF-8"><title>three_cameraProject</title><style>body {margin: 0;overflow: hidden;}</style><script src="three/build/three.js"></script><script src="three/examples/js/controls/OrbitControls.js"></script>
</head><body><script>function v4Project(v4, camera){return v4.clone().applyMatrix4(camera.matrixWorldInverse).applyMatrix4(camera.projectionMatrix);}var testCamera = new THREE.PerspectiveCamera(60, 1, 1, 20000);testCamera.position.set(0, 0, 100);testCamera.updateMatrixWorld();testCamera.updateProjectionMatrix();for(var i = 95; i <= 105; i ++){var proj = v4Project(new THREE.Vector4(2, 3, i), testCamera)console.log("z=" + i + "时，坐标为(" + proj.x + "," + proj.y + "." + proj.z + "," + proj.w + ")");}    </script>
</body>
</html>

这段代码创建了一个z坐标为100的透视相机，然后测试一个点坐标在100附近（95~105）变化时的投影结果。控制台输出如下：

我们看到，变化的只有z和w，并且均为单调递减，变化过程还比较平缓。但因为齐次坐标中，xyz最终都会除以w，所以最终的呈现结果就完全不一样了。分母越接近0，结果的绝对值越大，越趋向于无穷大，并且当分母从正数过渡到负数时，坐标值都会从正无穷突变到负无穷从而形成断层（数学上这叫无穷间断点）。

我们把区间取小一点，步长设短一点，并且改用Vector3的project方法进行测试

for(var i = 99; i <= 101; i +=0.125){var proj = new THREE.Vector3(2, 3, i).project(testCamera);console.log("z=" + i + "时，坐标为(" + proj.x + "," + proj.y + "." + proj.z + ")");
}

可以看到，从99到100，xyz的绝对值都飙升得很快。等于100的时候直接等于无穷大，因为此时的w等于0了。超过100就立马来个断层，变成负无穷大，然后绝对值又急剧下降回来。

从这里我们也可以看出，问题的本质

100是相机的z坐标，z=100时，物体刚好贴着相机，完全没距离，z>100时，物体在相机背面，完全不可见，所以这时候不管算出来的是啥值都不能说它错。但与此同时，它也是个不可用的数值。用我们技术大佬的话讲，这个结果只能用在逻辑的终点，而不能是中间的某个环节。

当然了，正交相机无需考虑这个问题，没透视变换的话，w始终等于1，不存在断层的情况。

来小结一下：

1 GPU渲染底层使用包含w的齐次坐标让开发者仅通过线性变换就能实现近大远小的非线性透视效果，非线性部分藏到了底层，w是分母。

2 project方法出问题的位置是在透视相机背面，跟视锥体范围无关，因为一个物体从相机正面到背面的移动过程中，分母w从一个很小的正数缓慢过渡到一个很小的负数，产生了断层，断层后的结果不可用。

3 一个坐标点在透视相机背面，是不会有一个正确的NDC坐标值，因此这个时候只能用来判断该点是否可见或出界，但不能再继续用它进行后续的计算。

4 THREE.Line2的shader通过trimSegment规避了越界的坐标点，但是射线检测没有做类似的处理，从而导致出界的线条存在射线检测错误的bug。

5 把LineMaterial上的trimSegment方法实现到LineSegments2的raycast方法中，问题就得到解决了。

THREE.Line2不是three.js主包的内容，而是在examples文件夹里面，尽管它也是官方提供的类，但是这样的目录规划不得不让笔者感觉到THREE.Line2更像个土八路，没入正编的样子。所以，这玩意儿还存在别的问题，下一篇我会给大家讲讲THREE.Line2的镜像问题，这又是一个大坑，请大家做好心理准备，嘿嘿！

相关文章：

three.js+WebGL踩坑经验合集(4.2):为什么不在可视范围内的3D点投影到2D的结果这么不可靠

上一篇&#xff0c;笔者留下了一个问题&#xff0c;three.js内置的THREE.Vector3.project方法算出来的结果对于超出屏幕可见范围的点来说错得相当离谱。 three.jsWebGL踩坑经验合集(4.1):THREE.Line2的射线检测问题&#xff08;注意本篇说的是Line2&#xff0c;同样也不是阈值…...

编程日记 2025/1/27 22:31:38

Kafka运维宝典 （二）- kafka 查看kafka的运行状态、broker.id不一致导致启动失败问题、topic消息积压量告警监控脚本

Kafka运维宝典 &#xff08;二&#xff09; 文章目录 Kafka运维宝典 &#xff08;二&#xff09;一、kafka broker.id冲突问题1. broker.id 冲突的影响2. 如何发现 broker.id 冲突3. 解决 broker.id 冲突的方法4. broker.id 配置管理5. 集群启动后确认 broker.id 唯一性6. brok…...

编程日记 2025/1/27 22:26:00

全球AI模型百科全书，亚马逊云科技Bedrock上的100多款AI模型

今天小李哥给大家介绍的是亚马逊云科技上的AI模型管理平台Amazon Bedrock上的Marketplace&#xff0c;这是亚马逊云科技在今年re:Invent发布的一个全新功能&#xff0c;将亚马逊的电商基因带到了其云计算平台&#xff0c;让我们能够通过Amazon Bedrock访问100多种流行、新兴和专…...

编程日记 2025/1/27 22:22:42

微信小程序中常见的 跳转方式 及其特点的表格总结（wx.navigateTo 适合需要返回上一页的场景）

文章目录 详细说明总结wx.navigateTo 的特点为什么 wx.navigateTo 最常用&#xff1f;其他跳转方式的使用频率总结 以下是微信小程序中常见的跳转方式及其特点的表格总结&#xff1a; 跳转方式API 方法特点适用场景wx.navigateTowx.navigateTo({ url: 路径 })保留当前页面&…...

编程日记 2025/1/27 22:21:37

【Elasticsearch】index:false

在 Elasticsearch 中&#xff0c;index 参数用于控制是否对某个字段建立索引。当设置 index: false 时&#xff0c;意味着该字段不会被编入倒排索引中&#xff0c;因此不能直接用于搜索查询。然而&#xff0c;这并不意味着该字段完全不可访问或没有其他用途。以下是关于 index:…...

编程日记 2025/1/27 22:07:15

新版IDEA创建数据库表

这是老版本的IDEA创建数据库表&#xff0c;下面可以自己勾选Not null&#xff08;非空),Auto inc&#xff08;自增长),Unique(唯一标识)和Primary key&#xff08;主键) 这是新版的IDEA创建数据库表&#xff0c;Not null和Auto inc可以看得到&#xff0c;但Unique和Primary key…...

编程日记 2025/1/27 22:03:02

输入带空格的字符串，求单词个数

输入带空格的字符串&#xff0c;求单词个数 __ueooe_eui_sjje__ ---->3syue__jdjd____die_ ---->3shuue__dju__kk ---->3 #include <stdio.h> #include <string.h>// 自定义函数来判断字符是否为空白字符 int isSpace(char c) {return c || c \t || …...

编程日记 2025/1/27 22:00:55

C语言程序设计十大排序—希尔排序

文章目录 1.概念✅2.希尔排序&#x1f388;3.代码实现✅3.1 直接写✨3.2 函数✨ 4.总结✅ 1.概念✅ 排序是数据处理的基本操作之一&#xff0c;每次算法竞赛都很多题目用到排序。排序算法是计算机科学中基础且常用的算法&#xff0c;排序后的数据更易于处理和查找。在计算机发展…...

编程日记 2025/1/27 21:58:48

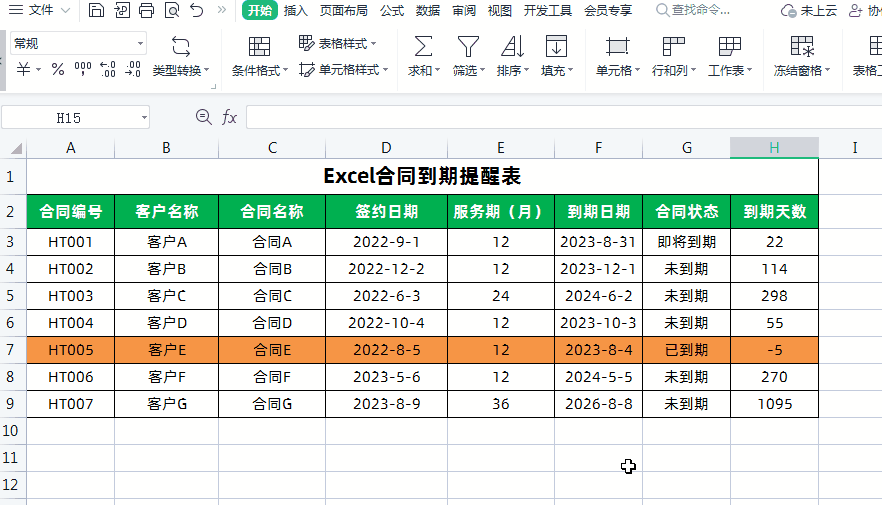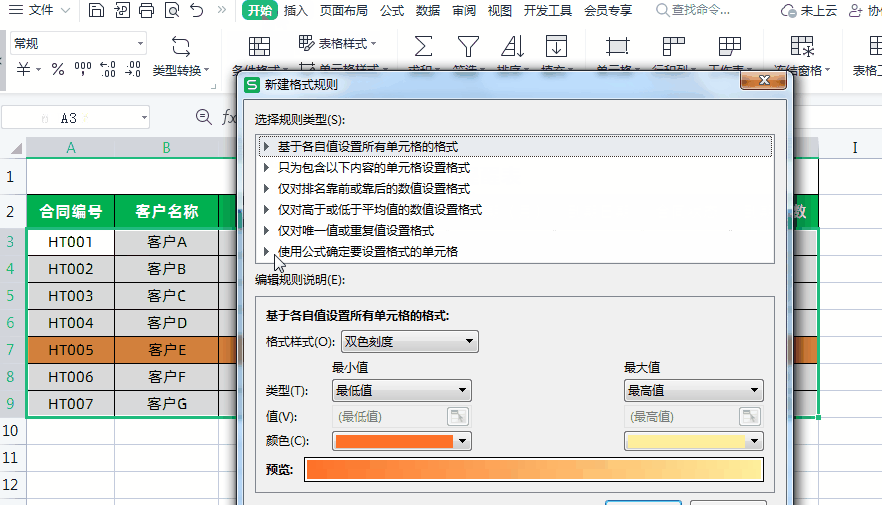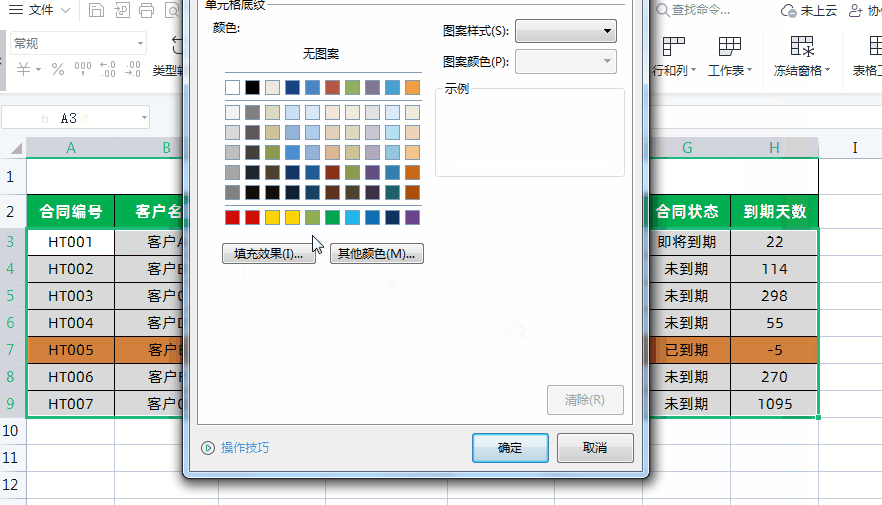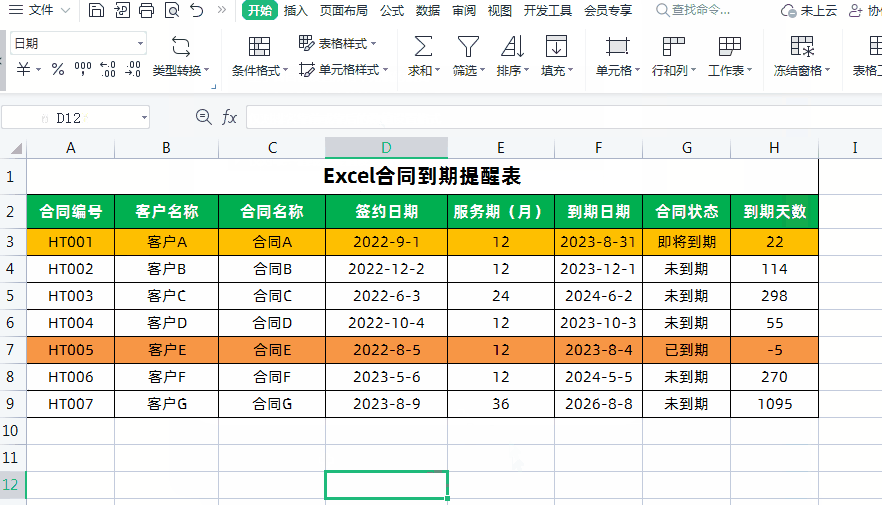
Excel制作合同到期自动提醒！

大家好&#xff0c;我是小鱼。 今天分享一下如何利用Excel制作合同到期提醒表&#xff0c;实现Excel表格自动计算合同到期日和天数&#xff0c;根据合同状态和到期天数自动填充颜色提醒&#xff0c;超实用。先看一下效果&#xff0c;已经到期的合同会自动被填充为红色&#xf…...

编程日记 2025/1/27 21:56:30

“AI质量评估系统：智能守护，让品质无忧

嘿&#xff0c;各位小伙伴们&#xff01;今天咱们来聊聊一个在现代社会中越来越重要的角色——AI质量评估系统。你知道吗&#xff1f;在这个快速发展的时代&#xff0c;产品质量已经成为企业生存和发展的关键。而AI质量评估系统&#xff0c;就像是我们的智能守护神&#xff0c;…...

编程日记 2025/1/27 21:55:25

爬虫基础之爬取某基金网站+数据分析

声明: 本案例仅供学习参考使用&#xff0c;任何不法的活动均与本作者无关 网站:天天基金网(1234567.com.cn) --首批独立基金销售机构-- 东方财富网旗下基金平台! 本案例所需要的模块: 1.requests 2.re(内置) 3.pandas 4.pyecharts 其他均需要 pip install 模块名 爬取步骤: …...

编程日记 2025/1/27 21:51:58

使用 Aryn DocPrep、DocParse 和 Elasticsearch 向量数据库实现高质量 RAG

作者&#xff1a;来自 Elastic Hemant Malik 及 Jonathan Fritz 组织依靠自然语言查询从非结构化数据中获取见解&#xff0c;但要获得高质量的答案&#xff0c;首先要进行有效的数据准备。Aryn DocParse 和 DocPrep通过将复杂文档转换为结构化 JSON 或 markdown 来简化此过程&a…...

编程日记 2025/1/27 21:43:33

Couchbase UI: Server

在 Couchbase UI 中的 Server&#xff08;服务器&#xff09;标签页主要用于管理和监控集群中的各个节点。以下是 Server 标签页的主要内容和功能介绍&#xff1a; 1. 节点列表 显示集群中所有节点的列表&#xff0c;每个节点的详细信息包括&#xff1a; 节点地址&#xff1…...

编程日记 2025/1/27 21:41:27

Web3.0时代的挑战与机遇：以开源2+1链动模式AI智能名片S2B2C商城小程序为例的深度探讨

摘要&#xff1a;Web3.0作为互联网的下一代形态&#xff0c;承载着去中心化、开放性和安全性的重要愿景。然而&#xff0c;其高门槛、用户体验差等问题阻碍了Web3.0的主流化进程。本文旨在深入探讨Web3.0面临的挑战&#xff0c;并提出利用开源21链动模式、AI智能名片及S2B2C商城…...

编程日记 2025/1/27 21:40:15

langchain基础（一）

模型又可分为语言模型&#xff08;擅长文本补全&#xff0c;输入和输出都是字符串&#xff09;和聊天模型&#xff08;擅长对话&#xff0c;输入时消息列表&#xff0c;输出是一个消息&#xff09;两大类。 以调用openai的聊天模型为例&#xff0c;先安装langchain_openai库 1…...

编程日记 2025/1/27 21:38:58

【Android】布局文件layout.xml文件使用控件属性android:layout_weight使布局较为美观，以RadioButton为例

目录 说明举例 说明 简单来说&#xff0c;android:layout_weight为当前控件按比例分配剩余空间。且单个控件该属性的具体数值不重要&#xff0c;而是多个控件的属性值之比发挥作用&#xff0c;例如有2个控件&#xff0c;各自的android:layout_weight的值设为0.5和0.5&#xff0…...

编程日记 2025/1/27 21:37:54

RabbitMQ 架构分析

文章目录 前言一、RabbitMQ架构分析1、Broker2、Vhost3、Producer4、Messages5、Connections6、Channel7、Exchange7、Queue8、Consumer 二、消息路由机制1、Direct Exchange2、Topic Exchange3、Fanout Exchange4、Headers Exchange5、notice5.1、备用交换机&#xff08;Alter…...

编程日记 2025/1/27 21:36:52

Qt Enter和HoverEnter事件

介绍 做PC开发的过程中或多或少都会接触到鼠标的悬停事件&#xff0c;Qt中处理鼠标悬停有Enter和HoverEnter两种事件 相同点 QEvent::Enter对应QEnterEvent&#xff0c;描述的是鼠标进入控件坐标范围之内的行为&#xff0c;QEnterEvent可以抓取鼠标的位置&#xff1b;QEvent…...

编程日记 2025/1/27 21:32:33

大语言模型之prompt工程

前言 随着人工智能的快速发展&#xff0c;我们正慢慢进入AIGC的新时代&#xff0c;其中对自然语言的处理成为了智能化的关键一环&#xff0c;在这个大背景下&#xff0c;“Prompt工程”由此产生&#xff0c;并且正逐渐成为有力的工具... LLM &#xff08;Large Language Mode…...

编程日记 2025/1/27 21:30:15

WPF基础 | WPF 常用控件实战：Button、TextBox 等的基础应用

WPF基础 | WPF 常用控件实战&#xff1a;Button、TextBox 等的基础应用 一、前言二、Button 控件基础2.1 Button 的基本定义与显示2.2 按钮样式设置2.3 按钮大小与布局 三、Button 的交互功能3.1 点击事件处理3.2 鼠标悬停与离开效果3.3 按钮禁用与启用 四、TextBox 控件基础4.…...

编程日记 2025/1/27 21:29:09

C++初阶-list的底层

目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

编程新知 2026/2/8 20:42:41

Linux链表操作全解析

Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表&#xff1f;1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

编程新知 2025/12/3 20:14:32

Python爬虫实战：研究feedparser库相关技术

1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代，互联网上存在着海量的信息资源。RSS（Really Simple Syndication）作为一种标准化的信息聚合技术，被广泛用于网站内容的发布和订阅。通过 RSS，用户可以方便地获取网站更新的内容，而无需频繁访问各个网站。 然而，互联网…...

编程新知 2025/8/18 9:54:31

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/2/9 1:38:05

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?

论文网址&#xff1a;pdf 英文是纯手打的&#xff01;论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误&#xff0c;若有发现欢迎评论指正&#xff01;文章偏向于笔记&#xff0c;谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

编程新知 2026/2/6 14:42:11

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

大数据学习（132）-HIve数据分析

​​​​&#x1f34b;&#x1f34b;大数据学习&#x1f34b;&#x1f34b; &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 用力所能及&#xff0c;改变世界。 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21

【Redis】笔记｜第8节｜大厂高并发缓存架构实战与优化

缓存架构 代码结构 代码详情 功能点&#xff1a; 多级缓存&#xff0c;先查本地缓存&#xff0c;再查Redis&#xff0c;最后才查数据库热点数据重建逻辑使用分布式锁&#xff0c;二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

编程新知 2026/1/26 3:45:28

基于Springboot+Vue的办公管理系统

角色&#xff1a; 管理员、员工 技术&#xff1a; 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能&#xff1a; 该办公管理系统是一个综合性的企业内部管理平台&#xff0c;旨在提升企业运营效率和员工管理水…...

编程新知 2026/1/31 8:55:37

云原生周刊：k0s 成为 CNCF 沙箱项目

开源项目推荐 HAMi HAMi&#xff08;原名 k8s‑vGPU‑scheduler&#xff09;是一款 CNCF Sandbox 级别的开源 K8s 中间件&#xff0c;通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度&#xff0c;为容器提供统一接口&#xff0c;实现细粒度资源配额…...

编程新知 2025/12/1 3:15:17