libOnvif通过组播不能发现相机
使用libOnvif库OnvifDiscoveryClient类,
auto discovery = new OnvifDiscoveryClient(QUrl(“soap.udp://239.255.255.250:3702”), cb.Build());
会有错误:
end of file or no input: message transfer interrupted or timed out(30 sec max recv delay)(30 sec max send delay)
组播地址是 239.255.255.250,如果使用相机IP,则可以发现相机soap规则。
成功过一次,然后第二天组播就发现不了相机,总是有上述错误。
- 卸载了virtualbox(能发现相机时,virtualbox已经存在)
- 关闭防火墙
- 禁用vmare的网卡
- 改相机(大华)的udp端口
- 删除网卡中其他IP,修改相机与本地网卡同一网段
均无没效果。
 onvif device test tool 扫描网址,可以得到信息,证明了就是程序组播存在问题。
onvif device test tool 扫描网址,可以得到信息,证明了就是程序组播存在问题。
搜索soap不能发现相机,有博友遇到不能往239.255.255.250发信息是virtualbox卸载了就正常,但是我已经卸载了。想卸载vmware又要使用。就打开以太网属性看看,看到火绒的驱动,把它禁用了。然后就正常了。。。,再启用它组播也正常。


相关文章:

libOnvif通过组播不能发现相机
使用libOnvif库OnvifDiscoveryClient类, auto discovery new OnvifDiscoveryClient(QUrl(“soap.udp://239.255.255.250:3702”), cb.Build()); 会有错误: end of file or no input: message transfer interrupted or timed out(30 sec max recv delay)…...
 :Table API SQL (一) 概览)
Flink (十二) :Table API SQL (一) 概览
Apache Flink 有两种关系型 API 来做流批统一处理:Table API 和 SQL。Table API 是用于 Scala 和 Java 语言的查询API,它可以用一种非常直观的方式来组合使用选取、过滤、join 等关系型算子。Flink SQL 是基于 Apache Calcite 来实现的标准 SQL。无论输入…...

FFmpeg(7.1版本)的基本组成
1. 前言 FFmpeg 是一个非常流行的开源项目,它提供了处理音频、视频以及其他多媒体内容的强大工具。FFmpeg 包含了大量的库,可以用来解码、编码、转码、处理和播放几乎所有类型的多媒体文件。它广泛用于视频和音频的录制、转换、流媒体传输等领域。 2. F…...

基于微信小程序的辅助教学系统的设计与实现
标题:基于微信小程序的辅助教学系统的设计与实现 内容:1.摘要 摘要:随着移动互联网的普及和微信小程序的兴起,基于微信小程序的辅助教学系统成为了教育领域的一个新的研究热点。本文旨在设计和实现一个基于微信小程序的辅助教学系统,以提高教…...

单片机基础模块学习——超声波传感器
一、超声波原理 左边发射超声波信号,右边接收超声波信号 左边的芯片用来处理超声波发射信号,中间的芯片用来处理接收的超声波信号 二、超声波原理图 T——transmit 发送R——Recieve 接收 U18芯片对输入的N_A1信号进行放大,然后输入给超声…...

HTML<hgroup>标签
例子: 使用hgroup元素标记标题和段落是相关的: <hgroup> <h2>Norway</h2> <p>The land with the midnight sun.</p> </hgroup> 定义和用法: 标签<hgroup>用于包围标题和一个或多个<p&g…...

C++并发编程指南08
以下是经过优化排版后的5.3节内容,详细解释了C中的同步操作和强制排序机制。每个部分都有详细的注释和结构化展示。 文章目录 5.3 同步操作和强制排序假设场景示例代码 5.3.1 同步发生 (Synchronizes-with)基本思想 5.3.2 先行发生 (Happens-before)单线程环境多线程…...
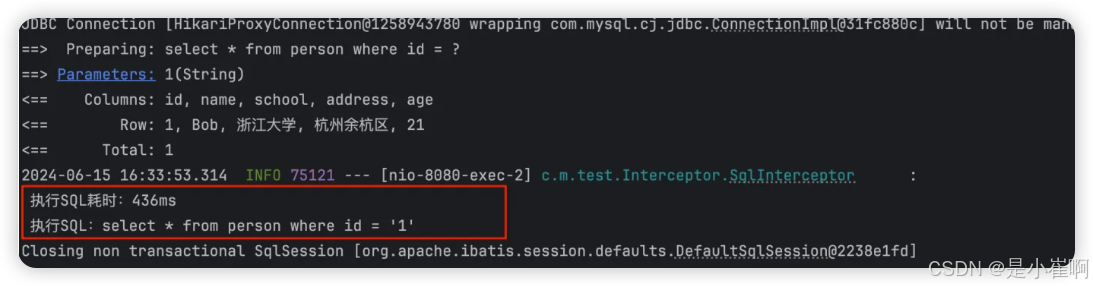
Spring Boot - 数据库集成03 - 集成Mybatis
Spring boot集成Mybatis 文章目录 Spring boot集成Mybatis一:基础知识1:什么是MyBatis2:为什么说MyBatis是半自动ORM3:MyBatis栈技术演进3.1:JDBC,自行封装JDBCUtil3.2:IBatis3.3:My…...

python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常…...

“星门计划对AI未来的意义——以及谁将掌控它”
“星门计划对AI未来的意义——以及谁将掌控它” 图片由DALL-E 3生成 就在几天前,唐纳德特朗普宣布了“星门计划”,OpenAI随即跟进,分享了更多细节。他们明确表示,计划在未来四年内投资5000亿美元,在美国为OpenAI构建一…...

为什么“记住密码”适合持久化?
✅ 特性 1:应用重启后仍需生效 记住密码的本质是长期存储用户的登录凭证(如用户名、密码、JWT Token),即使用户关闭应用、重启设备,仍然可以自动登录。持久化存储方案: React Native 推荐使用 AsyncStorag…...

国产SiC碳化硅功率器件技术成为服务器电源升级的核心引擎
在服务器电源应用中,国产650V碳化硅(SiC)MOSFET逐步取代传统超结(Super Junction, SJ)MOSFET,其核心驱动力源于SiC材料在效率、功率密度、可靠性和长期经济性上的显著优势,叠加产业链成熟与政策…...
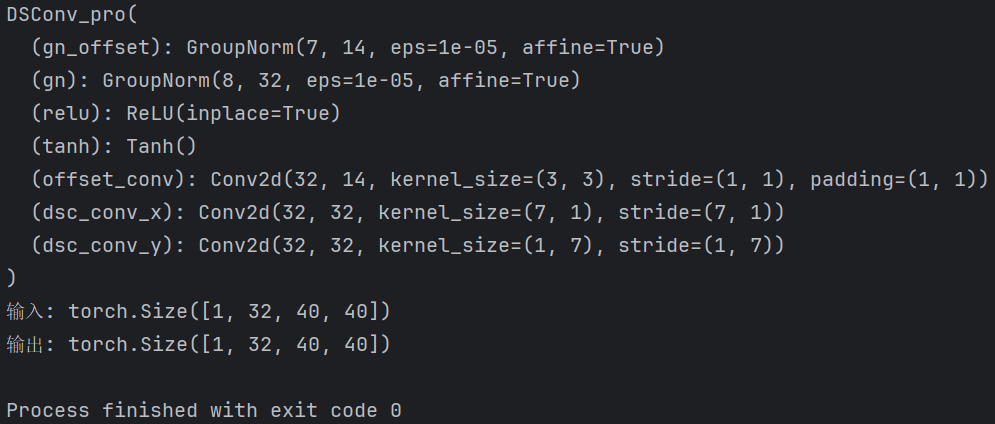
【Block总结】动态蛇形卷积,专注于细长和弯曲的局部结构|即插即用
论文信息 标题: Dynamic Snake Convolution based on Topological Geometric Constraints for Tubular Structure Segmentation 作者: 戚耀磊、何宇霆、戚晓明、张媛、杨冠羽 会议: 2023 IEEE/CVF International Conference on Computer Vision (ICCV) 发表时间: 2023年10月…...

Spring MVC 框架:构建高效 Java Web 应用的利器
Java学习资料 Java学习资料 Java学习资料 一、引言 在 Java Web 开发领域,Spring MVC 框架是一颗耀眼的明星。它作为 Spring 框架家族的重要成员,为开发者提供了一套强大而灵活的解决方案,用于构建 Web 应用程序。Spring MVC 遵循模型 - 视…...
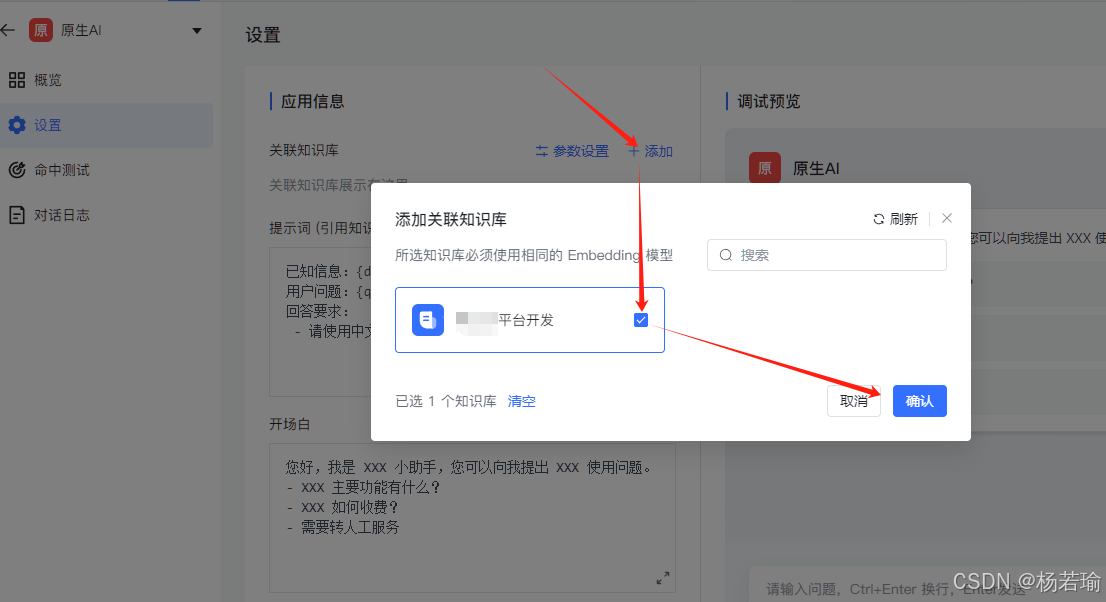
新鲜速递:DeepSeek-R1开源大模型本地部署实战—Ollama + MaxKB 搭建RAG检索增强生成应用
在AI技术快速发展的今天,开源大模型的本地化部署正在成为开发者们的热门实践方向。最火的莫过于吊打OpenAI过亿成本的纯国产DeepSeek开源大模型,就在刚刚,凭一己之力让英伟达大跌18%,纳斯达克大跌3.7%,足足是给中国AI产…...
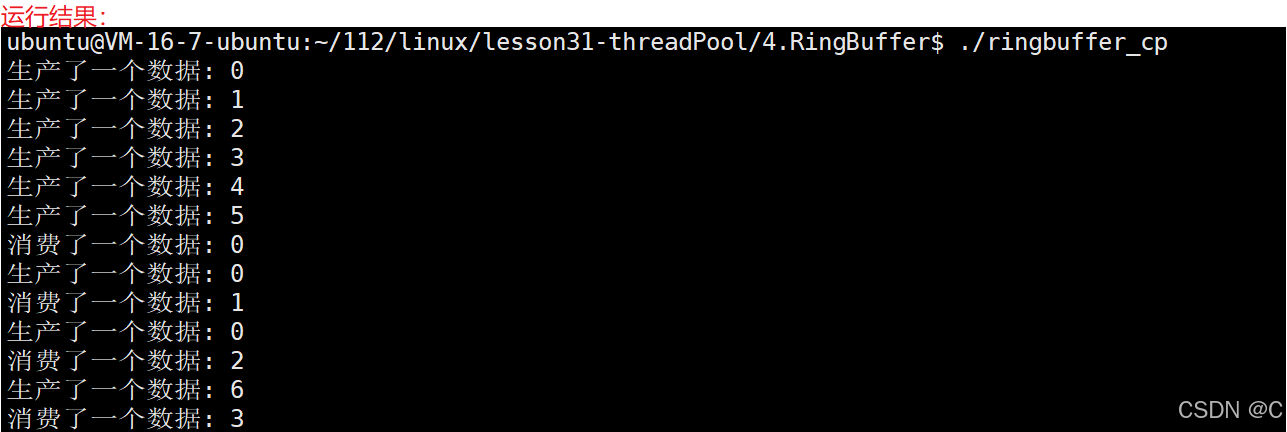
Linux_线程同步生产者消费者模型
同步的相关概念 同步:在保证数据安全的前提下,让线程能够按照某种特定的顺序访问临界资源,从而有效避免饥饿问题,叫做同步竞态条件:因为时序问题,而导致程序异常,我们称之为竞态条件。 同步的…...
Origami Agents:通过AI驱动的研究工具提升B2B销售效率
在当今竞争激烈的商业环境中,B2B销售团队面临着巨大的挑战,如何高效地发现潜在客户并进行精准的外展活动成为关键。Origami Agents通过其创新的AI驱动研究工具,正在彻底改变这一过程。本文将深入探讨Origami Agents的产品特性、技术架构以及其快速增长背后的成功因素。 一、…...

linux的/proc 和 /sys目录差异
/proc 和 /sys 都是Linux系统中用于提供系统信息和进行系统配置的虚拟文件系统,但它们的原理并不完全一样,以下是具体分析: 目的与功能 /proc :主要用于提供系统进程相关信息以及内核运行时的一些参数等,可让用户和程…...

AIGC时代的Vue或React前端开发
在AIGC(人工智能生成内容)时代,Vue开发正经历着深刻的变革。以下是对AIGC时代Vue开发的详细分析: 一、AIGC技术对Vue开发的影响 代码生成与自动化 AIGC技术使得开发者能够借助智能工具快速生成和优化Vue代码。例如,通…...

代码随想录算法训练营第三十九天-动态规划-337. 打家劫舍 III
老师讲这是树形dp的入门题目解题思路是以二叉树的遍历(递归三部曲)再结合动规五部曲dp数组如何定义:只需要定义一个二个元素的数组,dp[0]与dp[1] dp[0]表示不偷当前节点的最大价值dp[1]表示偷当前节点后的最大价值这样可以把每个节…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
