【数据结构】(8) 二叉树
一、树形结构
1、什么是树形结构
- 根节点没有前驱,其它节点只有一个前驱(双亲/父结点)。
- 所有节点可以有 0 ~ 多个后继,即分支(孩子结点)。
- 每个结点作为子树的根节点,这些子树互不相交。

2、关于树概念词
节点的度:节点的分支数。
树的度:树中最大的结点的度。
节点的层次:根为第一层。
树的高度:最大层次。
兄弟结点:同父的结点:
堂兄弟结点:同爷爷的结点。
节点的祖先:从根到该结点路径上的所有结点。
子孙:某节点为根,其子树中任意结点。
森林:互不相交的树集合。
3、树的表示形式
很多种,简单了解最常用(这种表示法,方便将树转为二叉树)的孩子兄弟表示法:
class Node {int data; // 存数据Node firstChild; // 存第一个孩子Node firstBrother; // 存第一个兄弟
} 二、二叉树
二、二叉树
1、什么是二叉树
- 树的度为2。
- 子树有左右之分,不能颠倒。
2、特殊的二叉树
- 满二叉树:若k表示结点层数,则每层结点数都等于 2^(k-1) 的树就是满二叉树。
- 完全二叉树:每个结点编号与满二叉树中每个节点编号一一对应的树。
3、二叉树性质
3.1、性质
- 第 k 层最多有 2^(k-1) 个结点。
- 高度为 k 的二叉树最多有 (2^k) - 1 个结点。
- 任意二叉树,叶子节点个数 n0 和有两个度的结点个数 n2 有关系:n0 = n2+1。
推导:n = n0+n1+n2 个结点,除了根节点都有前驱,故一共 n-1 个度。n-1 = 0*n0+1*n1+2*n2。
联合两个式子得到:n0 = n2 + 1。
- n 个节点的完全二叉树深度为 log(n+1) 上取整。
推导:n = (2^k)-1,k = log(n+1)。完全二叉树结点数肯定小于等于满二叉树结点数,所以 n 可能不够,结果就上取整。
- 从根节点开始(编号0),从左往右给每个结点编号:
① 双亲编号: i=0,根节点,无双亲;i>0,双亲编号=(i-1)/2。
② 左孩子编号:若 2*i+1 < n,左孩子编号 2*i+1;否则没左孩子。
③ 右孩子编号:若 2*i+2 < n,右孩子编号 2*i+2;否则没右孩子。
3.2、练习题



4、二叉树的遍历
4.1、遍历方式

前序:根>>左>>右,ABDCEF。
中序:左>>根>>右,DBAECF。
后序:左>>右>>根,DBEFCA。
层序:从上到下,从左往右,ABCDEF。
4.2、遍历序列转二叉树
如果想根据遍历序列获得二叉树,则必须是两种遍历序列,并且其中一种必须是中序遍历。因为,前、后、层序遍历序列能得知每个子二叉树的根;中序遍历能得知某根的左右子树。


4.3、代码(递归)
二叉树的存储结构有顺序存储和链式存储,本文只讨论了链式存储。顺序存储请看我写的优先级队列(堆)部分。
二叉树的表示形式:
public class BinaryTree {public static class TreeNode {char value;TreeNode left;TreeNode right;public TreeNode(char value) {this.value = value;}}private TreeNode root;............
}构造一棵二叉树(主要为了测试,这种构造方式不可取):

public void createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');A.left = B;A.right = C;B.left = D;C.left = E;C.right = F;root = A;}前序遍历:
public static void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.value + " ");preOrder(root.left);preOrder(root.right);}中序遍历:
public static void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.value + " ");inOrder(root.right);}后序遍历:
public static void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.value + " ");}4.4、代码(非递归):
前序遍历:144. 二叉树的前序遍历 - 力扣(LeetCode)
分析:深度优先遍历,左子树遍历完后,转到右子树,需要获得父亲结点,属于后进先出,用栈实现。
对于非空树:当前处理子树的根 cur 的初始值为 root。
step1:树不为空,树根 cur 入栈,并打印。若左子树不为空,更新子树 cur 为左子树,重复step1。直到遇到左子树为空,即 cur 为空停止上述循环。转到step2,开始判断右子树。
step2:弹出栈顶元素,即左子树的父结点,用于转到右子树,若右子树为空,重复step2。直到栈为空,且右子树仍为空时,树遍历完成;或者遇到右子树不为空,更新子树 cur 为右子树,重复 step1,开始遍历右子树。
class Solution {public List<Integer> preorderTraversal(TreeNode root) {Stack<TreeNode> stack = new Stack<>(); // 栈,用于左子树遍历完后,获取父节点,转到遍历右子树List<Integer> list = new ArrayList<>(); // 打印序列// 空树,不打印if(root == null) {return list;}TreeNode cur = root; // 当前处理子树的根。对于非空树,初始值为 root。// 栈不为空,说明还有右子树需要判断// cur不为空,说明还有非空右子树需要遍历while(!stack.isEmpty() || cur != null) { // step1// 一直是 push 操作,不需要判断栈空// 处理情况1:直到左子树为空,退出循环,再转到 step2// 处理情况2:右子树不为空,需要遍历右子树,转到 step1while(cur != null) {stack.push(cur); // 当前处理子树的根节点入栈list.add(cur.val); // 打印当前处理子树的根结点cur = cur.left; // 转到左子树}// step2cur = stack.pop(); // 弹出栈顶元素cur = cur.right; // 转到右子树}return list;}
}也可以用 ArrayDeque 替代 Stack,区别是 Stack 的方法有 synchronized 关键字修饰,在多线程环境中,用锁实现同步。比如:有一个 Stack 对象 p1,当一个线程使用了 p1调用的同步方法,那么 p1 对象的同步方法就会被锁住,使得其它的线程不能调用 p1 的同步方法;直到那个线程使用完后解锁,其它线程才能够使用。因此,在多线程环境中,Stack 相较于 ArrayDeque 是线程安全的。

中序遍历:94. 二叉树的中序遍历 - 力扣(LeetCode)
分析:左根右,根保存在栈中。先遍历左子树,左子树遍历完后,弹出根时打印根,最后遍历右子树。依然是用栈保存父节点,用于转向右子树。
方法与前序遍历类似,只不过打印根的位置不同。
class Solution {public List<Integer> inorderTraversal(TreeNode root) {Stack<TreeNode> stack = new Stack<>();List<Integer> list = new ArrayList<>(); if(root == null) {return list;}TreeNode cur = root; while(!stack.isEmpty() || cur != null) { while(cur != null) {stack.push(cur); cur = cur.left; }cur = stack.pop(); list.add(cur.val); // 弹出父节点(根结点)时,才打印根cur = cur.right; }return list;}
}后续遍历:145. 二叉树的后序遍历 - 力扣(LeetCode)
分析:左右根,左子树遍历完后,父节点不能弹出栈,右子树遍历完后,父节点再弹出栈打印。

我们现在需要思考,右子树遍历完的标志是什么。比如上图这棵树,在遍历到 F 时,栈中元素应该为:A, C, F。当前父节点 F 的左子树为 null 不遍历,右子树也为 null 不遍历,弹出根 F 并打印,此时栈为:A,C。当前父节点 C 的右子树是F,F已遍历完,需要弹出根C并打印......
可以观察到,当前父节点(栈顶元素)的右子树为空,或者父节点的右孩子是上一次弹出的栈顶元素时, 表示右子树遍历结束。
class Solution {public List<Integer> postorderTraversal(TreeNode root) {Stack<TreeNode> stack = new Stack<>();List<Integer> list = new ArrayList<>(); if(root == null) {return list;}TreeNode cur = root; TreeNode pre = null; // 存储上一次遍历完成的子树的根while(!stack.isEmpty() || cur != null) { while(cur != null) {stack.push(cur); cur = cur.left; }TreeNode top = stack.peek(); // 查看父节点元素,继续判断是否要遍历右子树// 父节点的右孩子为空,或者父节点的右孩子是上一次遍历完的子树(上一次弹出的根),则表示其右子树遍历完成// cur 不能改变,仍为 null,表示右子树已经遍历完了,不需要再在step1中遍历。所以用 top 暂存父节点if(top.right == null || top.right == pre) {stack.pop(); // 弹出父节点list.add(top.val); // 打印父节点pre = top; // 保存遍历完的子树的根} else { // 右子树没遍历完,继续遍历父节点的右子树cur = top.right; }}return list;}
}层序遍历:使用队列,根节点开始,从上往下,从左到右,先进先出。每弹出一个结点,打印该节点,让后将其孩子全部依次入队。直到队列为空结束。
public void levelOrder() {Queue<TreeNode> queue = new LinkedList<>(); // 队列if (root == null) { // 空树return;}queue.offer(root); // 根节点入队while (!queue.isEmpty()) {TreeNode node = queue.poll(); // 出队System.out.print(node.value + " "); // 打印if (node.left!= null) { // 左孩子不为空,入队queue.offer(node.left);}if (node.right!= null) { // 右孩子不为空,入队queue.offer(node.right);}}}5、二叉树的基本操作
5.1、求树中节点个数
遍历思想:把遍历中的打印结点,换为计数结点。
private int count; public int size() {count = 0;size(root);return count;}public void size(TreeNode root) {if (root == null) {return;}count++;size(root.left);size(root.right);}子问题思想:树的结点树=左数结点数+右数结点数+1。
public static int size2(TreeNode root) {if (root == null) { // 空树,0个结点return 0;}return size2(root.left) + size2(root.right) + 1;}5.2、求叶子节点个数
遍历思想:把打印结点换为,是叶子结点就计数。
private int leafCount;public int leafCount() {leafCount = 0;leafCount(root);return leafCount;}public void leafCount(TreeNode root) {if (root == null) {return;}if (root.left == null && root.right == null) {leafCount++;} leafCount(root.left);leafCount(root.right);}子问题思想:树的叶子结点个数=左子树叶子节点个数+右子树叶子节点个数。
public static int leafCount2(TreeNode root) {if (root == null) { // 空树,0个叶子节点return 0;}if (root.left == null && root.right == null) { // 只有一个根结点,1个叶子节点return 1;}return leafCount2(root.left) + leafCount2(root.right);}5.3、求第K层结点个数
遍历思想:把打印结点换成,是第 K 层结点就计数。(遍历整棵树。)
private int levelCount;public int levelCount(int k) {levelCount = 0;levelCount(root, k);return levelCount;}public void levelCount(TreeNode root, int k) {if (root == null) {return;}if (k == 1) {levelCount++;}levelCount(root.left, k - 1);levelCount(root.right, k - 1);}子问题思想:树的第K层结点个数=左子树的第K-1层节点个数+右子树的第K-1层节点个数。(如果K合法,到第K层为止,效率比遍历思想更高。)
public static int levelCount2(TreeNode root, int k) {if (root == null) { // 空树,没有节点return 0;}if (k == 1) { // 树的第一层结点为根,1个节点return 1;}return levelCount2(root.left, k - 1) + levelCount2(root.right, k - 1);}5.3、求二叉树的高度
子问题思想:树的高度=max(左子树高度,右子树高度)+1。
时间复杂度=调用递归函数的次数=O(n)。
空间复杂度,因为调用到叶子节点后,就会释放空间,再遍历另一个分叉,因此空间复杂度是树的高度=O(logN)。
public static int height(TreeNode root) {if (root == null) { // 空树,深度为0return 0;}return Math.max(height(root.left), height(root.right)) + 1;}5.4、检测 value 是否在树中
子问题思想:是根,返回根节点地址;搜索左子树,返回值不为空,返回地址;搜索右子树,返回值不为空,返回地址;否者,返回 nll。
最坏时间复杂度:O(N)
public static TreeNode findValue(TreeNode root, char value) {if (root == null) { // 树为空,没有结点return null; }if (root.value == value) { // 是根节点return root;}TreeNode left = findValue(root.left, value); // 搜索左子树if (left!= null) { // 找到了return left;}return findValue(root.right, value); // 搜索右子树}5.5、判断树是否为完全二叉树
思路:空树必为完全二叉树。层序遍历树,空结点要入队。遇到第一个空结点,如果是完全二叉树,则在队列中,这个空结点的右边必全是空结点;如果不是完全二叉树,在队列中,其右必存在不为空结点。
故遇到空结点后,马上在队列中判断其后是否都为空,是则为完全二叉树;否则不为。

public static boolean isComplete(TreeNode root) {if(root == null) { // 空树return true;}Queue<TreeNode> queue = new LinkedList<>(); // 队列queue.offer(root); // 根节点入队while (!queue.isEmpty()) { // 层序遍历树,寻找树中第一个空结点TreeNode node = queue.poll(); // 弹出一个结点if (node != null) {queue.offer(node.left); // 左孩子入队queue.offer(node.right); // 右孩子入队} else { // 遇到空结点,退出循环break;}}// 判断空结点后是否都为空姐点while (!queue.isEmpty()) {if (queue.poll() != null) { // 还有非空结点,不是完全二叉树return false;}}return true;}6、二叉树相关OJ题
6.1、分层包装
102. 二叉树的层序遍历 - 力扣(LeetCode)
![]()

分析:在正常前序遍历的基础上,根节点入队,得到初始队列。>> 依次出队,包装为一层,添加到树中。其孩子依次入队,作为下一层。>> 重复上述操作,直到下一层为空。

class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList<>();if(root == null) { // 空树return list;}// 初始,根节点入队Queue<TreeNode> queue = new LinkedList<>(); // 下一层队列queue.offer(root); while(!queue.isEmpty()) { // 直到下一层为空List<Integer> curLevel = new ArrayList<>(); // 当前层 int size = queue.size(); // 处理下一层,下一层作为当前层的大小while(size-- != 0) { // 遍历队列,包装为层,将每个结点的孩子放入下一层TreeNode node = queue.poll(); // 弹出一个结点curLevel.add(node.val); // 包装到当前层中if(node.left != null) { // 左孩子放入下一层queue.offer(node.left);}if(node.right != null) { // 右孩子放入下一层queue.offer(node.right);}}list.add(curLevel);}return list;}
}6.2、两颗相同的树
100. 相同的树 - 力扣(LeetCode)
分析:子问题思想。两根为空,必相同。一根为空,一根不为空,必不相同。两根不为空,两值不同,必不相同;两值相同,两棵树的左子树相同且右子树相同,则相同,否则不同。
时间复杂度:O(min(n, m)),最坏情况,结点数最少的那棵树遍历完,就知道是否相同了。
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) { // 两空树,相同return true;}if((p == null && q != null) || (p != null && q == null)) { // 一根空,一根不空,不相同return false;}// 两根不为空if(p.val != q.val) { // 值不相同,不相同return false;}// 两根相同,左、右子树相同才相同;否则不同return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}
}6.3、另一棵树的子树
572. 另一棵树的子树 - 力扣(LeetCode)

分析:子问题思想。树为空,没有子树;子树与树相同,是子树;子树与树不相同,子树是不是树的左子树的子树,是则是子树;子树是不是树的右子树的子树,是则是子树;否则不是子树。
时间复杂度:O(m*n),每遇树中一个结点,就遍历子树是否与之相等。m 个结点比较 m 次,每次比较 n 个子树结点。
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) { // 两空树,相同return true;}if((p == null && q != null) || (p != null && q == null)) { // 一根空,一根不空,不相同return false;}// 两根不为空if(p.val != q.val) { // 值不相同,不相同return false;}// 两根相同,左、右子树相同才相同;否则不同return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);}public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null) { // 树为空,没有子树return false;}if (isSameTree(root, subRoot)) { // 树和子树相同,是树的子树return true;}if(isSubtree(root.left, subRoot)) { // 是左子树的子树,是树的子树return true;}return isSubtree(root.right, subRoot); // 是右子树的子树,是树的子树;否则不是树的子树}
}6.4、翻转二叉树
226. 翻转二叉树 - 力扣(LeetCode)

分析:如果为空或者只有一个根节点,不翻转;否则,左子树和右子树交换,继续翻转左子树、右子树。
class Solution {public TreeNode invertTree(TreeNode root) {// 如果树为空,或者只有一个根节点,不翻转if(root == null || (root.left == null && root.right == null)) {return root;}// 否则左子树和右子树交换TreeNode tmp = root.left;root.left = root.right;root.right = tmp;// 翻转左子树、右子树invertTree(root.left);invertTree(root.right);return root;}
}6.5、判断平衡二叉树
110. 平衡二叉树 - 力扣(LeetCode)
平衡二叉树:每一棵子树的左右子树的高度差不超过1。
分析:空树,是平衡二叉树。左子树是平衡二叉树,且右子树是平衡二叉树,左子树的高度和右子树的高度差的绝对值≤1,是平衡二叉树;否则不是。
时间复杂度:O(N^2),对于树中每个结点,都要求其左、右子树的高度;每次求子树高度,都会遍历整棵子树。
class Solution {public int height(TreeNode root) {if (root == null) { // 空树,深度为0return 0;}return Math.max(height(root.left), height(root.right)) + 1;}public boolean isBalanced(TreeNode root) {// 空树是平衡二叉树if(root == null) {return true;}// 左子树不是平衡二叉树,或者右子树不是平衡二叉树,则树不是平衡二叉树if(!isBalanced(root.left) || !isBalanced(root.right)) {return false;}// 左右子树高度差的绝对值≤1,是平衡二叉树,否则不是return Math.abs(height(root.left) - height(root.right)) <= 1;}
}改进:其实,求树的高度就包含了求子树的高度;但是上面的代码重复求了子树的高度。改进思路就是,我们只需求一次树的高度,在此过程中必然历经,求子树、子子树高度,在求到它们高度的之后,马上判断它们的高度差的绝对值是否≤1,它们是否是平衡二叉树。
时间复杂度:O(N)。只求了一次树的高度,遍历了所有结点。
class Solution {/*** 返回值:-1 表示不为平衡二叉树,大于 -1 表示树的高度。*/private int height(TreeNode root) {if (root == null) { // 空树,深度为0return 0;}// 求左、右子树高度int leftH = height(root.left);int rightH = height(root.right);// 求完高度,马上判断是否符合平衡二叉树的要求// 左、右子树是否为平衡二叉树if(leftH == -1 || rightH == -1) {return -1;}// 左右子树高度差是否符合要求if(Math.abs(leftH - rightH) > 1) {return -1;}// 左、右子树符合平衡二叉树要求,返回树的高度return Math.max(leftH, rightH) + 1;}public boolean isBalanced(TreeNode root) {// 空树是平衡二叉树if(root == null) {return true;}// 如果返回值 > -1,表示是树高度,是平衡二叉树;否则不是return height(root) > -1;}
}6.6、判断对称二叉树
101. 对称二叉树 - 力扣(LeetCode)


分析:子问题思路。空树,对称。非空树,对于左、右子树根节点,都为空,则对称;一个为空、一个不为空,则不对称;都不为空,但是值不相等,则不对称;都不为空,且值相等,左根的左子树与右根的右子树对称,且左根的右子树与右根的左子树对称,则树对称;否则不对称。
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null) { // 空树,对称return true;}return isSymmetricChild(root.left, root.right);}public boolean isSymmetricChild(TreeNode leftRoot, TreeNode rightRoot) {// 左根、右根都为空,对称if(leftRoot == null && rightRoot == null) {return true;}// 左、右根其中一个不为空,另一个为空,不对称if((leftRoot == null && rightRoot != null) || (leftRoot != null && rightRoot == null)) {return false;}// 左右根不为空,但值不等,不对称if(leftRoot != null && rightRoot != null && leftRoot.val != rightRoot.val) {return false;}// 左根的左子树、右根的右子树对称,且左根的右子树、右根的左子树对称,才对称return isSymmetricChild(leftRoot.left, rightRoot.right) && isSymmetricChild(leftRoot.right, rightRoot.left);}
}6.7、先序构建,中序遍历
二叉树遍历_牛客题霸_牛客网

分析:重点在根据先序遍历序列构建二叉树。因为这里告诉了空结点,所以只有一个先序遍历序列也能构建二叉树。
遍历思想。先序遍历,如果根节点是'#',则返回 null;如果根节点不是'#',则创建结点,到下一个字符,创建左子树、创建右子树,最后返回根节点。

import java.util.Scanner;class TreeNode {char value;TreeNode left;TreeNode right;public TreeNode(char value) {this.value = value;}
}public class Main {public static int i; // 记录字符下标// 先序创建树public static TreeNode createTree(String str) {TreeNode root = null;if (str.charAt(i) != '#') {root = new TreeNode(str.charAt(i)); // 创建新节点i++;// 创建左、右子树root.left = createTree(str);root.right = createTree(str);} else {i++;}return root;}// 中序遍历public static void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.value + " ");inOrder(root.right);}public static void main(String[] args) {Scanner in = new Scanner(System.in);while (in.hasNextLine()) {String str = in.nextLine();i = 0;TreeNode root = createTree(str);inOrder(root);}}
}6.8、最近公共祖先
236. 二叉树的最近公共祖先 - 力扣(LeetCode)

分析:根据题目,树中必有p、q两节点。如果 p 在左子树中,q 在右子树中,则 root 为最近公共祖先。

如果 p、q 中存在一个是根结点,则 root 为最近公共祖先。

如果 p、q 都在左子树中,进入左子树找最近公共祖先。

如果 p、q 都在右子树中,进入右子树找最近公共祖先。

时间复杂度:O(N)
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {// 如果为空树,没有最近公共祖先// 必须加此判断,遇到叶子结点,递归函数才能返回 nullif(root == null) {return null;}// 其中一个是根节点,最近公共祖先是根if(p == root || q == root) {return root;}TreeNode leftFather = lowestCommonAncestor(root.left, p, q);TreeNode rightFather = lowestCommonAncestor(root.right, p, q);// p、q 分布在左、右两子树中,最近公共祖先是根if(leftFather != null && rightFather != null) {return root;}// 最近公共祖先在左子树中if(leftFather != null) {return leftFather;}// 最近公共祖先在右子树中if(rightFather != null) {return rightFather;}// 树中不存在 q、preturn null;}
}思路2:找到根节点分别到 p、q 的路径,对比路径,找到最近公共祖先。

p 的路径:3、5、6。size=3
q 的路径:3、5、2、4。size=4
q 路径出栈 4-3=1 个元素,得到 3、5、2。
p 、q 同时出栈,不相同则继续同时出栈,相同则找到最近公共祖先。
时间复杂度:O(N^2),找了两次路径。
class Solution {public boolean getPath(TreeNode root, TreeNode target, Stack<TreeNode> stack) {if(root == null) { // 空树,没有路径return false;}stack.push(root); // 根节点入栈if(root == target) { // 找到目标节点,退出return true;}boolean found = getPath(root.left, target, stack); // 在左子树中寻找路径if(found) { // 找到路径,退出return true;}found = getPath(root.right, target, stack); // 在右子树中寻找路径if(found) { // 找到路径,退出return true;}stack.pop(); // 路径没找到,根结点出栈return false;}public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {Stack<TreeNode> stack = new Stack<>();Stack<TreeNode> stack2 = new Stack<>();getPath(root, p, stack); // 寻找 p 的路径getPath(root, q, stack2); // 寻找 q 的路径// 计算路径长度差,长的路径先出栈差的绝对值长度int len = stack.size() - stack2.size();if(len < 0) { // 长度差为负,交换两个栈Stack<TreeNode> temp = stack;stack = stack2;stack2 = temp;len = -len;}// 弹出栈中元素,直到长度差为0while(len-- != 0) {stack.pop();}// 弹出栈中元素,不相同则继续弹,相同则为最近公共祖先while(!stack.isEmpty() && !stack2.isEmpty() && stack.peek() != stack2.peek()) {stack.pop();stack2.pop();}return stack.isEmpty()? null : stack.peek(); // 栈为空,没有最近公共祖先}
}6.9、根据前序、中序构造树
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)

分析:前序遍历从左往右,找根节点,创建根节点。再在中序遍历中找根节点的位置,区分左右子树。再构建左子树,构建右子树。
class Solution {private int preIndex; // 先序序列的根下标public TreeNode buildTree(int[] preorder, int[] inorder) {return buildTree(preorder, inorder, 0, inorder.length-1);}private int findIndex(int[] inorder, int low, int high, int rootVal) {for(int i = low; i <= high; i++) {if(inorder[i] == rootVal) {return i;}}return -1;}// low、high 为在中序序列中子树的起始、终止下标private TreeNode buildTree(int[] preorder, int[] inorder, int low, int high) {if(low > high) { // 没有结点了,返回空return null;}int rootVal = preorder[preIndex]; // 根TreeNode root = new TreeNode(rootVal); // 创建根结点preIndex++;int inIndex = findIndex(inorder, low, high, rootVal); // 在中序序列中找根的位置// 构建左、右子树root.left = buildTree(preorder, inorder, low, inIndex-1);root.right = buildTree(preorder, inorder, inIndex+1, high);return root;}
}6.10、根据中序、后序遍历构造树
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
分析:方法与 6.9 大致相同,只不过后序序列是从后往前遍历根。后序:左右根,倒着遍历,会先创建右子树。
class Solution {private int postIndex; // 后序序列的根下标public TreeNode buildTree(int[] inorder, int[] postorder) {postIndex = postorder.length-1;return buildTree(postorder, inorder, 0, inorder.length-1);}private int findIndex(int[] inorder, int low, int high, int rootVal) {for(int i = low; i <= high; i++) {if(inorder[i] == rootVal) {return i;}}return -1;}// low、high 为在中序序列中子树的起始、终止下标private TreeNode buildTree(int[] postorder, int[] inorder, int low, int high) {if(low > high) { // 没有结点了,返回空return null;}int rootVal = postorder[postIndex]; // 根TreeNode root = new TreeNode(rootVal); // 创建根结点postIndex--;int inIndex = findIndex(inorder, low, high, rootVal); // 在中序序列中找根的位置// 构建左、右子树root.right = buildTree(postorder, inorder, inIndex+1, high);root.left = buildTree(postorder, inorder, low, inIndex-1);return root;}
}6.11、根据二叉树创建字符串



分析:前序遍历,同一棵子树中的结点会被()包在一起。空树,不打印。非空树,打印根节点,如果左右孩子都为空,什么都不打印。如果左孩子不为空,右孩子为空,打印(,遍历左子树,打印)。如果左孩子为空,右孩子不为空,打印()(,遍历右子树,打印)。如果左右孩子都不为空,打印(,遍历左子树,打印)(,遍历右子树,打印)。
class Solution {public String tree2str(TreeNode root) {StringBuilder str = new StringBuilder();tree2str(root, str);return str.toString();}public void tree2str(TreeNode root, StringBuilder str) {// 空树,不打印if (root == null) {return;}str.append(root.val); // 打印根节点// 如果左孩子不为空,打印(,遍历左子树,打印)if (root.left != null) {str.append('(');tree2str(root.left, str);str.append(')');// 如果右孩子为空,什么都不打印// 如果右孩子不为空,打印(,遍历右子树,打印)// if(root.right != null) {// str.append('(');// tree2str(root.right, str);// str.append(')');// }} else {// 如果右子树为空,什么都不打印// 如果右子树不为空,打印(),打印(,遍历右子树,打印)if (root.right != null) {str.append("()");// str.append('(');// tree2str(root.right, str);// str.append(')');}}if (root.right != null) {str.append('(');tree2str(root.right, str);str.append(')');}}
}相关文章:

【数据结构】(8) 二叉树
一、树形结构 1、什么是树形结构 根节点没有前驱,其它节点只有一个前驱(双亲/父结点)。所有节点可以有 0 ~ 多个后继,即分支(孩子结点)。每个结点作为子树的根节点,这些子树互不相交。 2、关于…...

navicat导出表结构到Excel 带字段备注
navicat导出表结构到Excel 带字段备注 SELECTCOLUMN_NAME AS 字段名称,COLUMN_TYPE AS 字段类型, IF( IS_NULLABLE NO, 否, 是 ) AS 是否必填,COLUMN_COMMENT AS 注释 FROMINFORMATION_SCHEMA.COLUMNS WHERE -- 数据库名table_schema vmscenter -- 表名AND table_name y…...

使用pocketpal-ai在手机上搭建本地AI聊天环境
1、下载安装pocketpal-ai 安装github的release APK 2、安装大模型 搜索并下载模型,没找到deepseek官方的,因为海外的开发者上传了一堆乱七八糟的deepseek qwen模型,导致根本找不到官方上传的……deepseek一开源他们觉得自己又行了。 点击之…...

程序诗篇里的灵动笔触:指针绘就数据的梦幻蓝图<10>
大家好啊,我是小象٩(๑ω๑)۶ 我的博客:Xiao Xiangζั͡ޓއއ 很高兴见到大家,希望能够和大家一起交流学习,共同进步。 今天我们继续来复习指针… 目录 一、看一段代码二、 一维数组传参的本质三、冒泡排序3.1 基本思想四、二…...

FPGA简介|结构、组成和应用
Field Programmable Gate Arrays(FPGA,现场可编程逻辑门阵列),是在PAL、GAL、CPLD等可编程器件的基础上进一步发展的产物, 是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,…...

[c语言日寄]在不完全递增序中查找特定要素
【作者主页】siy2333 【专栏介绍】⌈c语言日寄⌋:这是一个专注于C语言刷题的专栏,精选题目,搭配详细题解、拓展算法。从基础语法到复杂算法,题目涉及的知识点全面覆盖,助力你系统提升。无论你是初学者,还是…...

Golang的多团队协作编程模式与实践经验
Golang的多团队协作编程模式与实践经验 一、多团队协作编程模式概述 在软件开发领域,多团队协作编程是一种常见的工作模式。特别是对于大型项目来说,不同团队间需要协同合作,共同完成复杂的任务。Golang作为一种高效、并发性强的编程语言&…...

cv2.Sobel
1. Sobel 算子简介 Sobel 算子是一种 边缘检测算子,通过对图像做梯度计算,可以突出边缘。 Sobel X 方向卷积核: 用于计算 水平方向(x 方向) 的梯度。 2. 输入图像示例 假设我们有一个 55 的灰度图像,像素…...

Windows软件自动化利器:pywinauto python
Pywinauto WindowsAPP UI自动化 Windows软件自动化利器:pywinauto python...

关于 IoT DC3 中驱动(Driver)的理解
在开源IoT DC3物联网系统中,驱动(Driver)扮演着至关重要的角色,它充当了软件系统与物理设备之间的桥梁。驱动的主要功能是依据特定的通信协议连接到设备,并根据设备模板中配置的位号信息进行数据采集和指令控制。不同的…...

LogicFlow自定义节点:矩形、HTML(vue3)
效果: LogicFlow 内部是基于MVVM模式进行开发的,分别使用preact和mobx来处理 view 和 model,所以当我们自定义节点的时候,需要为这个节点定义view和model。 参考官方文档:节点 | LogicFlow 1、自定义矩形节点 custo…...

多模态本地部署ConVideoX-5B模型文生视频
文章目录 一、多模态概念1.多模态学习2. 人机交互3. 健康医疗4. 内容创作和娱乐 二、模型介绍三、环境安装1. 安装工具包2. 模型下载 四、运行代码五、代码解析六、效果生成七. 总结1. 模型介绍2. 部署环境3. 部署步骤4. 生成视频5. 应用场景 一、多模态概念 多模态࿰…...

html 点击弹出视频弹窗
一、效果: 点击视频按钮后,弹出弹窗 播放视频 二、代码 <div class="index_change_video" data-video-src="</...

业务干挂数据库,Oracle内存分配不足
📢📢📢📣📣📣 作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验 Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、MySQL、PG、高斯…...

MongoDB 7 分片副本集升级方案详解(下)
#作者:任少近 文章目录 1.4 分片升级1.5 升级shard11.6 升级shard2,shard31.7 升级mongos1.8重新启用负载均衡器1.9 推荐MongoDB Compass来验证数据 2 注意事项: 1.4 分片升级 使用“滚动”升级从 MongoDB 7.0 升级到 8.0,即在其他成员可用…...

Webpack相关优化总结
在使用webpack时提供了各种配置,这里结合在业务中常用的配置汇总一下可以进行的一系列的webpack优化 缩小文件搜索范围 其原理是在构建时,会以用户配置的Entry为开始依次递归遍历每个Module,在遍历每个Module时会调用相应合适的Loader对原模…...

ollama实践笔记
目录 一、linux安装文件命令: 二、启动ollama 三、linux 如何把ollama serve做为服务方式启动 四、安装deepseek-r1 五、如何在网页中使用ollama? 5.1 安装Open WebUI【不推荐】 5.2 安装ollama-webui-lite 六、Ubuntu安装docker、只需要一句话…...

springCloud-2021.0.9 之 服务调服务 示例
文章目录 前言springCloud-2021.0.9 之 服务调服务 示例1. 主要用到的组件2. 效果3. 源码3.1. 服务A3.2. 服务B接受接口 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每…...
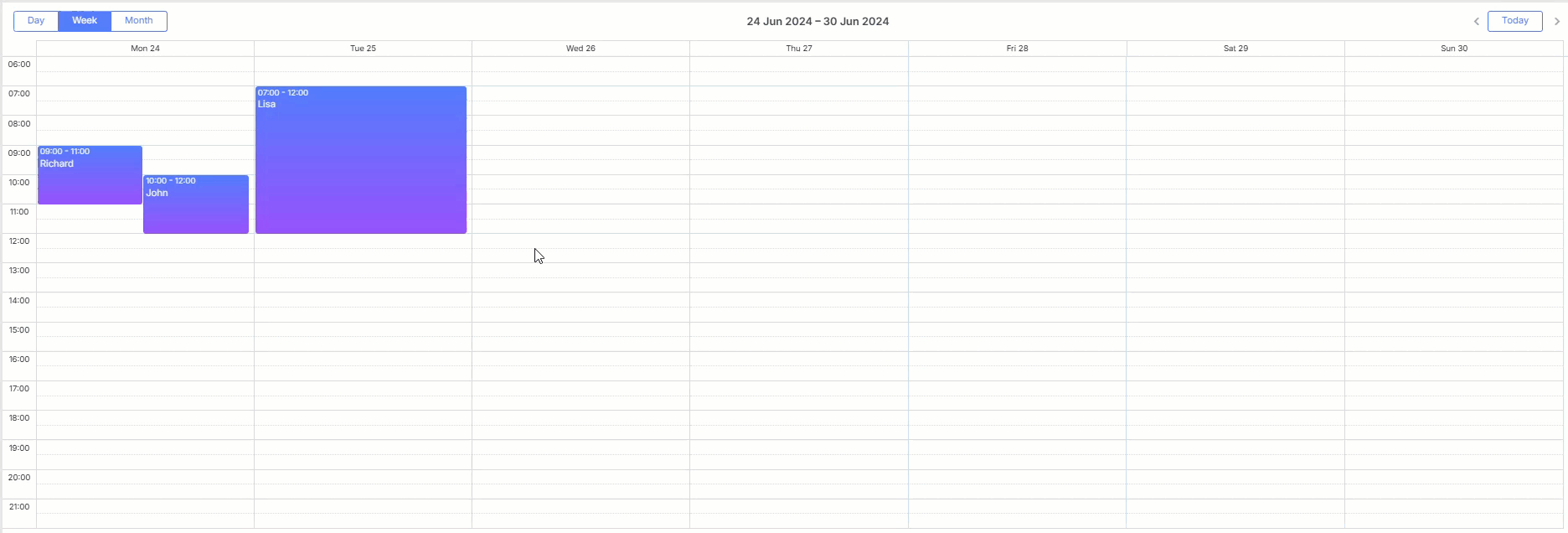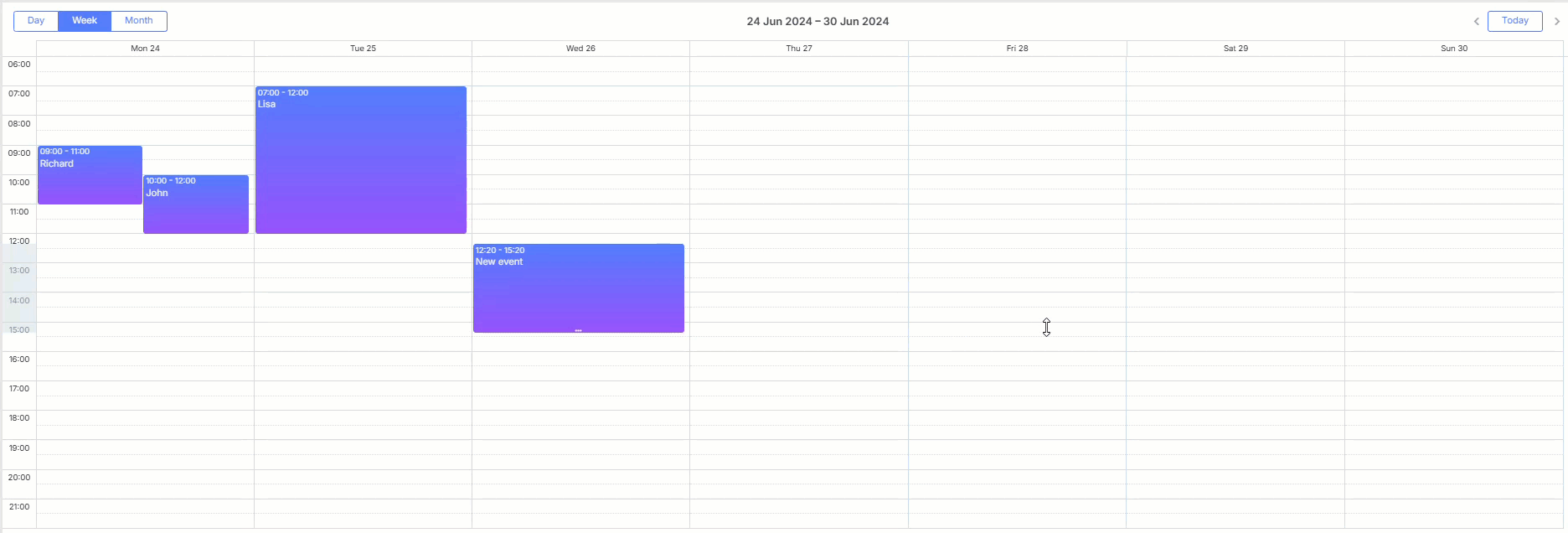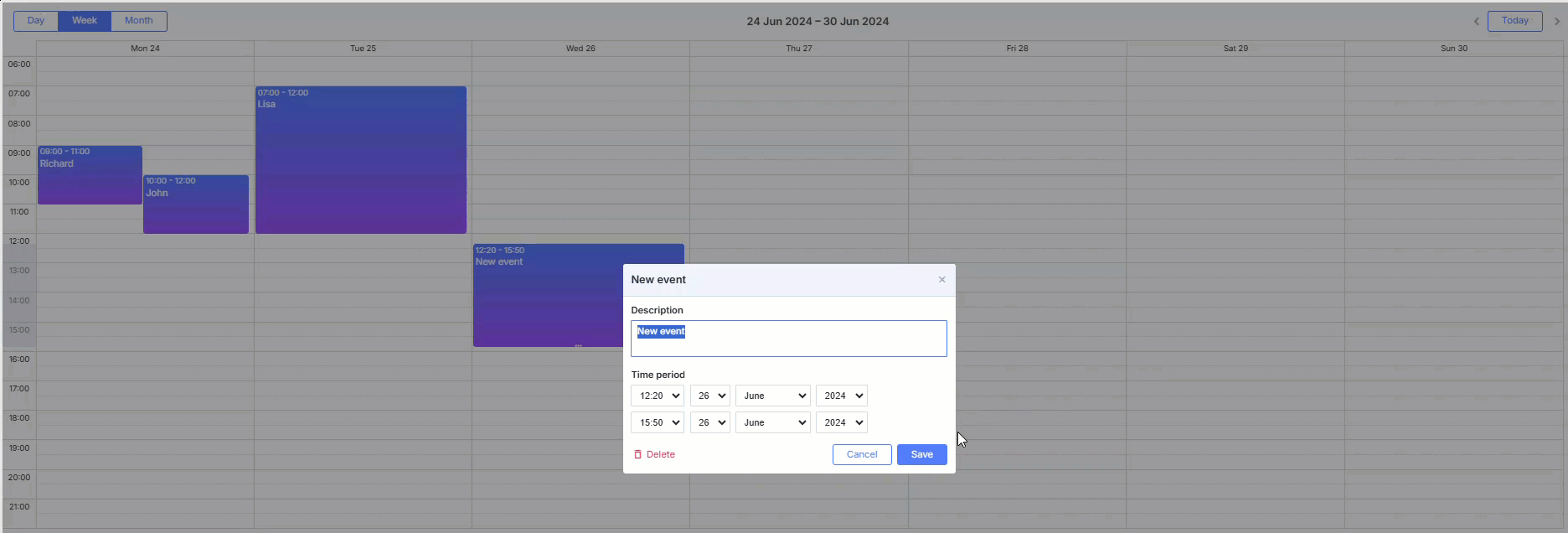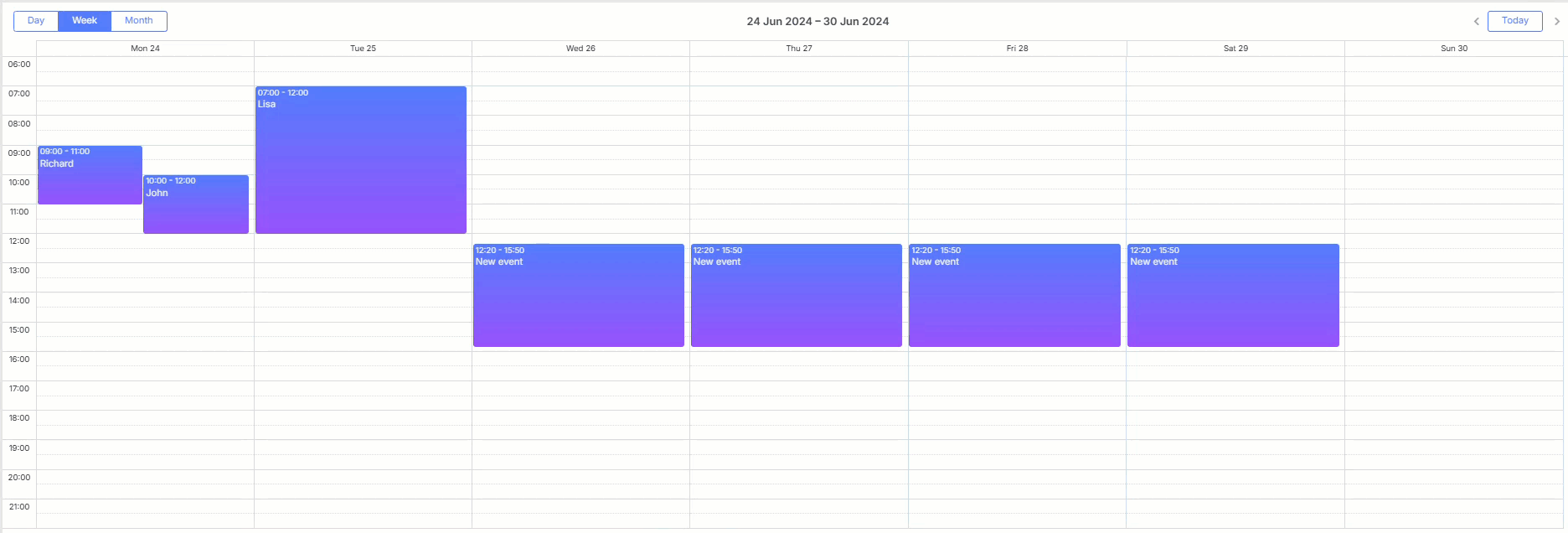
如何使用DHTMLX Scheduler的拖放功能,在 JS 日程安排日历中创建一组相同的事件
DHTMLX Scheduler 是一个全面的调度解决方案,涵盖了与规划事件相关的广泛需求。假设您在我们的 Scheduler 文档中找不到任何功能,并且希望在我们的 Scheduler 文档中看到您的项目。在这种情况下,很可能可以使用自定义解决方案来实现此类功能。…...

QxOrm生成json
下载Qxorm-1.5版本 使用vs打开项目,直接生成即可: lib目录中会生成dll和lib文件 新建Qt项目使用Qxorm: 将QxOrm中上面三个目录拷贝到新建的Qt项目中 pro文件添加使用QxOrm第三方库 INCLUDEPATH $$PWD/include/ LIBS -L"$$PWD/lib" LIBS…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
