牛客网算法八股刷题系列(七)正则化(软间隔SVM再回首)
牛客网算法八股刷题系列——正则化[软间隔SVM再回首]
- 题目描述
- 正确答案:C\mathcal CC
- 题目解析
- 开端:关于函数间隔问题解释的补充
- 软间隔SVM\text{SVM}SVM
- Hinge\text{Hinge}Hinge损失函数
- 支持向量机的正则化
题目描述
关于支持向量机(Support Vector Machine,SVM)(\text{Support Vector Machine,SVM})(Support Vector Machine,SVM),下列说法错误的是()(\quad)()
AL2\mathcal A \quad L_2AL2正则项,作用是最大化分类间隔,使得分类器拥有更强的泛化能力
BHinge\mathcal B \quad \text{Hinge}BHinge损失函数,作用是最小化经验风险错误
C\mathcal C \quadC分类间隔1∣∣W∣∣\begin{aligned}\frac{1}{||\mathcal W||}\end{aligned}∣∣W∣∣1,其中∣∣W∣∣||\mathcal W||∣∣W∣∣代表向量的模
DL1\mathcal D \quad L_1DL1正则化对所有参数的惩罚力度都一样,可以让一部分权重变为零,因此产生稀疏模型,能够去除某些特征
正确答案:C\mathcal CC
题目解析
开端:关于函数间隔问题解释的补充
该部分对照支持向量机——模型构建思路进行阅读。
这里依然以二分类任务为例。已知数据集合D\mathcal DD以集合内的标签集合表示如下:
D={(x(i),y(i))}i=1Ny(i)∈{+1,−1}\mathcal D = \{(x^{(i)},y^{(i)})\}_{i=1}^N \quad y^{(i)} \in \{+1,-1\}D={(x(i),y(i))}i=1Ny(i)∈{+1,−1}
在支持向量机——模型构建思路介绍了分类正确的标志:模型输出结果WTx(i)+b\mathcal W^Tx^{(i)} + bWTx(i)+b与对应标签结果y(i)y^{(i)}y(i)同号:
{WTx(i)+b>0y(i)=+1WTx(i)+b<0y(i)=−1\begin{cases} \mathcal W^Tx^{(i)} + b > 0 \quad y^{(i)} = +1 \\ \mathcal W^T x^{(i)} + b < 0 \quad y^{(i)} = -1 \end{cases}{WTx(i)+b>0y(i)=+1WTx(i)+b<0y(i)=−1
从而确定模型的决策边界(超平面):
WTx+b=0\mathcal W^Tx + b = 0WTx+b=0
虽然找到了决策边界,但出现了新的问题:决策边界不唯一。我们可以对上述决策边界进行任意缩放 ⇒\Rightarrow⇒ 等式两侧同时乘以常数kkk,决策边界并不发生影响。
k⋅(WTx+b)=k⋅0=0k \cdot (\mathcal W^Tx + b) = k \cdot 0 = 0k⋅(WTx+b)=k⋅0=0
但是对应的函数间隔(Functional Margin)H(i)=y(i)(WTx(i)+b)(x(i),y(i)∈D)(\text{Functional Margin}) \mathcal H^{(i)} = y^{(i)}(\mathcal W^Tx^{(i)} + b) \quad (x^{(i)},y^{(i)} \in \mathcal D)(Functional Margin)H(i)=y(i)(WTx(i)+b)(x(i),y(i)∈D)发生了变化:
{Original : H(i)=y(i)(WTx(i)+b)Expand/Reduce : k⋅H(i)=y(i)[k⋅(WTx(i)+b)]\begin{cases} \text{Original : } \mathcal H^{(i)} = y^{(i)}(\mathcal W^Tx^{(i)} + b) \\ \text{Expand/Reduce : } k \cdot \mathcal H^{(i)} = y^{(i)} \left[k \cdot (\mathcal W^Tx^{(i)} + b)\right] \end{cases}{Original : H(i)=y(i)(WTx(i)+b)Expand/Reduce : k⋅H(i)=y(i)[k⋅(WTx(i)+b)]
不同的决策边界,会导致某个样本点会存在多个函数间隔的判别结果。这意味着:仅通过WTx(i)+b\mathcal W^Tx^{(i)} + bWTx(i)+b和y(i)y^{(i)}y(i)同号这个约束,没有办法让模型收敛。通过对函数间隔的描述,可以通过公式对该描述进行表达:
∃γ>0⇒minx(i),y(i)∈Dy(i)(WTx(i)+b)=minx(i),y(i)DH(i)=γ\exist \gamma > 0 \Rightarrow \mathop{\min}\limits_{x^{(i)},y^{(i)} \in \mathcal D} y^{(i)}(\mathcal W^Tx^{(i)} + b) = \mathop{\min}\limits_{x^{(i)},y^{(i)}\mathcal D} \mathcal H^{(i)} = \gamma∃γ>0⇒x(i),y(i)∈Dminy(i)(WTx(i)+b)=x(i),y(i)DminH(i)=γ
为了方便计算,设定γ=1\gamma = 1γ=1。也就是说,无论对决策边界扩张还是收缩,都可以通过对W,b\mathcal W,bW,b进行相应的缩放,使得等式成立:
由于W,b\mathcal W,bW,b都是向量,缩放变换后的W′,b′\mathcal W',b'W′,b′必然和原结果线性相关。并没有影响对权重特征的描述。该部分见《机器学习(周志华著)》P122 左侧小字解释部分
minx(i),y(i)∈Dy(i)(WTx(i)+b)=1⇔y(i)(WTx(i)+b)≥1\mathop{\min}\limits_{x^{(i)},y^{(i)} \in \mathcal D} y^{(i)}(\mathcal W^Tx^{(i)} + b) = 1 \Leftrightarrow y^{(i)} (\mathcal W^Tx^{(i)} + b) \geq 1x(i),y(i)∈Dminy(i)(WTx(i)+b)=1⇔y(i)(WTx(i)+b)≥1
最终可将支持向量机——最大间隔分类器表示为如下基本型:
{minW,b12∣∣W∣∣2s.t.y(i)(WTx(i)+b)≥1(x(i),y(i))∈D\begin{cases} \begin{aligned}\mathop{\min}\limits_{\mathcal W,b} \frac{1}{2} ||\mathcal W||^2\end{aligned} \\ s.t. \quad y^{(i)}(\mathcal W^Tx^{(i)} + b) \geq 1 \quad (x^{(i)},y^{(i)}) \in \mathcal D \end{cases}⎩⎨⎧W,bmin21∣∣W∣∣2s.t.y(i)(WTx(i)+b)≥1(x(i),y(i))∈D
软间隔SVM\text{SVM}SVM
该部分对照支持向量机——软间隔SVM\text{SVM}SVM进行阅读。
关于软间隔构建损失函数的动机 可描述为:
- 假设损失函数为L\mathcal LL,如果某样本被划分正确,那么对应的L=0\mathcal L = 0L=0;
- 相反,如果某样本没有被划分正确,意味着y(i)(WTx(i)+b)<1y^{(i)}(\mathcal W^Tx^{(i)} + b) < 1y(i)(WTx(i)+b)<1,那么对应的函数结果为:
可以看出,该结果是一个≤1\leq 1≤1的正值。
(x(i),y(i))⇒L(i)=1−y(i)(WTx(i)+b)(x^{(i)},y^{(i)}) \Rightarrow \mathcal L^{(i)} = 1 - y^{(i)}(\mathcal W^Tx^{(i)} + b)(x(i),y(i))⇒L(i)=1−y(i)(WTx(i)+b)
可以看出,该损失函数大于等于000恒成立,并且这些正值是由划分错误的样本累积起来产生的。
基于上述动机,我们尝试使用0/10/10/1损失函数描述上述两种情况:
该函数的特点:无论划分错误的偏差有多大,都被一视同仁为数值111.
L0/1[y(i)(WTx(i)+b)−1]={1y(i)(WTx(i)+b)−1<00Otherwise\mathcal L_{0/1}\left[y^{(i)}(\mathcal W^Tx^{(i)} + b) - 1\right] = \begin{cases} 1 \quad y^{(i)}(\mathcal W^Tx^{(i)} + b) - 1 < 0 \\ 0 \quad \text{Otherwise} \end{cases}L0/1[y(i)(WTx(i)+b)−1]={1y(i)(WTx(i)+b)−1<00Otherwise
从而对应拉格朗日函数可描述为如下形式:
依然是‘拉格朗日乘数法’。
minW,b12∣∣W∣∣2+C∑x(i),y(i)∈DL0/1[y(i)(WTx(i)+b)−1]\mathop{\min}\limits_{\mathcal W,b} \frac{1}{2} ||\mathcal W||^2 + \mathcal C\sum_{x^{(i)},y^{(i)} \in \mathcal D}\mathcal L_{0/1} \left[y^{(i)}(\mathcal W^Tx^{(i)} + b) - 1\right]W,bmin21∣∣W∣∣2+Cx(i),y(i)∈D∑L0/1[y(i)(WTx(i)+b)−1]
Hinge\text{Hinge}Hinge损失函数
由于0/10/10/1损失函数在定义域内并非处处连续,在优化过程中因无法处处可导导致无法求解出迭代最优解;并且∑x(i),y(i)∈DL0/1[y(i)(WTx(i)+b)−1]\sum_{x^{(i)},y^{(i)} \in \mathcal D}\mathcal L_{0/1} \left[y^{(i)}(\mathcal W^Tx^{(i)} + b) - 1\right]∑x(i),y(i)∈DL0/1[y(i)(WTx(i)+b)−1]的结果是一个正整数,对于划分错误的样本偏差描述得不够细致。
因此,另一种方法是将偏差值直接作为损失函数的一部分,具体数学描述表示如下:
L={0y(i)(WTx(i)+b)≥11−y(i)(WTx(i)+b)Otherwise\mathcal L = \begin{cases} 0 \quad y^{(i)}(\mathcal W^Tx^{(i)} + b) \geq 1 \\ 1 - y^{(i)}(\mathcal W^Tx^{(i)} + b) \quad \text{Otherwise} \end{cases}L={0y(i)(WTx(i)+b)≥11−y(i)(WTx(i)+b)Otherwise
和上述0/10/10/1损失函数的动机相比,该函数在以y(i)(WTx(i)+b)y^{(i)}(\mathcal W^Tx^{(i)} + b)y(i)(WTx(i)+b)的定义域内处处连续,并且该方法累积的偏差是真实的偏差结果。将上述两种情况使用一个公式进行表达:
LHinge=max{0,1−y(i)(WTx(i)+b)}\mathcal L_{Hinge} = \max \left\{0,1 - y^{(i)}(\mathcal W^Tx^{(i)} + b)\right\}LHinge=max{0,1−y(i)(WTx(i)+b)}
该函数的图像表示为如下形式:

该函数由于形似一个开合的书页,也被称作合页损失函数(Hinge Loss Function\text{Hinge Loss Function}Hinge Loss Function),记作LHinge\mathcal L_{Hinge}LHinge。最终,基于该函数的拉格朗日函数可描述为如下形式:
minW,b12∣∣W∣∣2+C∑x(i),y(i)∈Dmax{0,1−y(i)(WTx(i)+b)}\mathop{\min}\limits_{\mathcal W,b} \frac{1}{2}||\mathcal W||^2 + \mathcal C \sum_{x^{(i)},y^{(i)} \in \mathcal D} \max \left\{0,1 - y^{(i)}(\mathcal W^Tx^{(i)} + b) \right\}W,bmin21∣∣W∣∣2+Cx(i),y(i)∈D∑max{0,1−y(i)(WTx(i)+b)}
支持向量机的正则化
上面介绍了两种损失函数:0/10/10/1损失函数,合页损失函数。实际上,无论是哪种损失函数,我们关注的是它们整体的优化目标,也就是拉格朗日函数。
{minW,b12∣∣W∣∣2+C∑x(i),y(i)∈DL0/1[y(i)(WTx(i)+b)−1]minW,b12∣∣W∣∣2+C∑x(i),y(i)∈Dmax{0,1−y(i)(WTx(i)+b)}\begin{cases} \begin{aligned}\mathop{\min}\limits_{\mathcal W,b} \frac{1}{2} ||\mathcal W||^2 + \mathcal C\sum_{x^{(i)},y^{(i)} \in \mathcal D}\mathcal L_{0/1} \left[y^{(i)}(\mathcal W^Tx^{(i)} + b) - 1\right] \end{aligned}\\ \begin{aligned} \mathop{\min}\limits_{\mathcal W,b} \frac{1}{2}||\mathcal W||^2 + \mathcal C \sum_{x^{(i)},y^{(i)} \in \mathcal D} \max \left\{0,1 - y^{(i)}(\mathcal W^Tx^{(i)} + b) \right\} \end{aligned} \end{cases}⎩⎨⎧W,bmin21∣∣W∣∣2+Cx(i),y(i)∈D∑L0/1[y(i)(WTx(i)+b)−1]W,bmin21∣∣W∣∣2+Cx(i),y(i)∈D∑max{0,1−y(i)(WTx(i)+b)}
观察上述两个函数,它们存在共性:
- 第一项:都是通过调整合适的参数W∗\mathcal W^*W∗,并尽可能使最大间隔∣∣W∣∣2||\mathcal W||^2∣∣W∣∣2达到最小;
- 第二项:针对划分错误样本产生的误差(L0/1,LHinge)(\mathcal L_{0/1},\mathcal L_{Hinge})(L0/1,LHinge)达到最小。
关于上述拉格朗日函数的通式表示如下:
详见《机器学习》(周志华著) P133 6.5 支持向量回归 公式6.42
minfΩ(f)+C∑x(i),y(i)∈DL[f(x(i)),y(i)]\mathop{\min}\limits_{f} \Omega(f) + \mathcal C \sum_{x^{(i)},y^{(i)} \in \mathcal D} \mathcal L[f(x^{(i)}),y^{(i)}]fminΩ(f)+Cx(i),y(i)∈D∑L[f(x(i)),y(i)]
- 我们通常称第一项Ω(f)\Omega(f)Ω(f)为结构风险(Structual Risk\text{Structual Risk}Structual Risk),在支持向量机中结构风险是指对模型fff的结构——最大间隔逻辑进行优化;
- 第二项被称为经验风险(Empirical Risk\text{Empirical Risk}Empirical Risk),具体描述模型与数据之间的契合程度。Hinge\text{Hinge}Hinge函数作为减小经验风险的损失函数,B\mathcal B \quadB 选项正确。
至此,我们要纠正两个误区:
-
真正的损失函数指的是经验风险。通过观察,结构风险∣∣W∣∣2||\mathcal W||^2∣∣W∣∣2自身 就是正则化的表达形式。因此,正则化的功能都能在结构风险中进行表达。
这里关于 A\mathcal A \quadA 选项中选择L2L_2L2正则化项描述最大间隔的逻辑正确。
-
关于结构风险∣∣W∣∣2||\mathcal W||^2∣∣W∣∣2,它并不是∣∣W∣∣2||\mathcal W||_2∣∣W∣∣2,在之前关于∣∣W∣∣2=WTW||\mathcal W||^2 = \mathcal W^T\mathcal W∣∣W∣∣2=WTW只是选择了L2L_2L2正则化进行示例。实际上,在描述最大间隔的时候,不一定仅使用欧氏距离。在K-Means\text{K-Means}K-Means算法介绍中提到过明可夫斯基距离,比较有代表性的是曼哈顿距离,对应的L1L_1L1正则化;以及欧式距离,对应L2L_2L2正则化。
在正则化——权重衰减角度(直观现象)中补充了L1L_1L1正则化稀疏权重特征的过程。在迭代过程中,L1L_1L1正则化产生的权重点仅让一部分权重分量描述,而剩余的权重分量没有参与,从而导致权重分量尽量稀疏;
一部分权重分量没有发挥作用,对应的权重结果就是000。
并且L1L_1L1正则化对应所有权重分量均是一次项,对应的权重分量不会出现非线性的提高/打压,因而L1L_1L1对权重的惩罚力度相同,D\mathcal D \quadD 选项正确。
相反,L2L_2L2正则化会倾向于将迭代的权重分摊在各个权重分量 上使各分量取值尽量平衡。从而使非零分量的数量更加稠密。
C\mathcal C \quadC 选项中的1∣∣W∣∣\begin{aligned}\frac{1}{||\mathcal W||}\end{aligned}∣∣W∣∣1描述的是支持向量到最优决策边界的距离;而分类间隔表示最优决策边界两侧支持向量之间的距离。即2×1∣∣W∣∣=2∣∣W∣∣\begin{aligned}2 \times \frac{1}{||\mathcal W||}= \frac{2}{||\mathcal W||}\end{aligned}2×∣∣W∣∣1=∣∣W∣∣2。因此 C\mathcal C \quadC 选项错误。
求解过程详见支持向量机——模型求解.
相关参考:
《机器学习》(周志华著)
相关文章:

牛客网算法八股刷题系列(七)正则化(软间隔SVM再回首)
牛客网算法八股刷题系列——正则化[软间隔SVM再回首]题目描述正确答案:C\mathcal CC题目解析开端:关于函数间隔问题解释的补充软间隔SVM\text{SVM}SVMHinge\text{Hinge}Hinge损失函数支持向量机的正则化题目描述 关于支持向量机(Support Vector Machine…...

开源即时通讯IM框架MobileIMSDK的微信小程序端开发快速入门
一、理论知识准备 您需要对微信小程序开发有所了解: 1)真正零基础入门学习笔记系列2)从零开始的微信小程序入门教程3)最全教程:微信小程序开发入门详解 您需要对WebSocket技术有所了解: 1)新…...

【C++从0到1】11、C++中赋值运算
C从0到1全系列教程 1、赋值运算 运算符示例描述c a b;将把a b的值赋给c。 把右边操作数的值赋给左边操作数。c a;相当于 c c a; 加且赋值运算符,把右边操作数加上左边操作数的结果赋值给左边操作数。-c - a;相当于 c c - a; 减且赋值运算符,把左…...
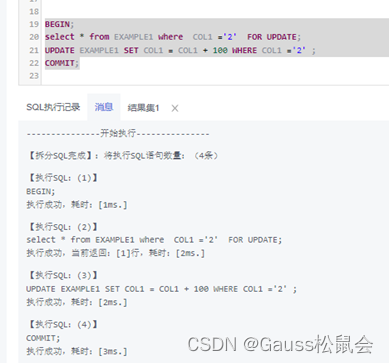
GaussDB数据库事务介绍
目录 一、前言 二、GaussDB事务的定义及应用场景 三、GaussDB事务的管理 四、GaussDB事务语句 五、GaussDB事务隔离 六、GaussDB事务监控 七、总结 一、前言 随着大数据和互联网技术的不断发展,数据库管理系统的作用越来越重要,实现数据的快速读…...

MYSQL——美团面试题
MYSQL——美团面试题 2023/3/27 美团二面 题目描述 Create table If Not Exists courses (student varchar(255), class varchar(255));insert into courses (student, class) values (A, Math); insert into courses (student, class) values (B, English); insert into co…...

Python 小型项目大全 16~20
#16 钻石 原文:http://inventwithpython.com/bigbookpython/project16.html 这个程序的特点是一个小算法,用于绘制各种尺寸的 ASCII 艺术画钻石。它包含绘制轮廓或你指定大小的填充式菱形的功能。这些功能对于初学者来说是很好的练习;试着理解…...
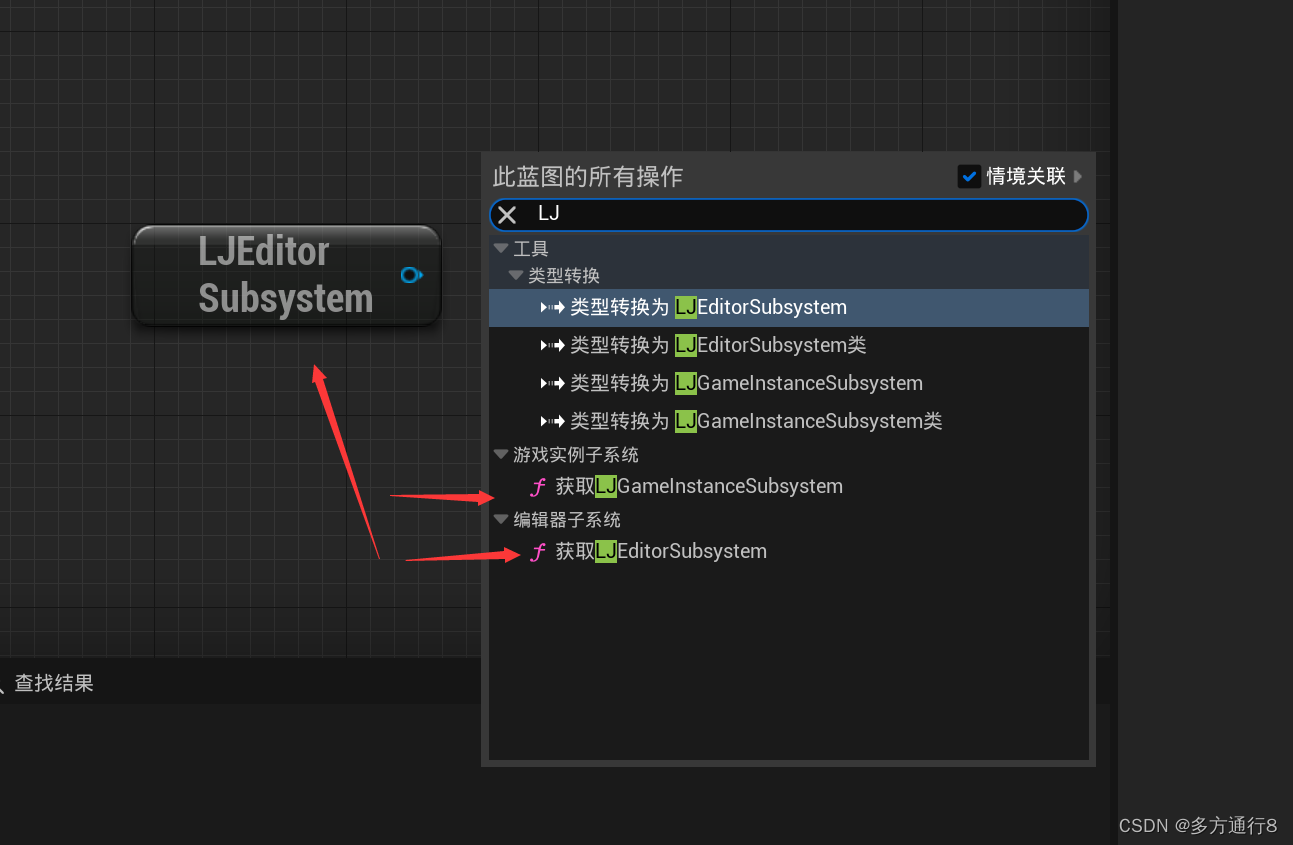
UE4/5C++之SubSystem的了解与创建
目录 了解生命周期 为什么用他,简单讲解? SubSystems创建和使用 创建SubSystems中的UGamelnstanceSubsystem类: 写基本的3个函数: 在蓝图中的样子: 创建SubSystems中的UEditorSubsystem类: SubSyste…...
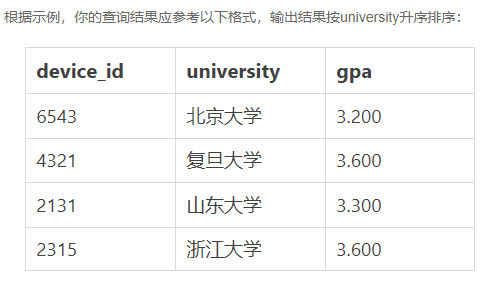
牛客网在线编程SQL篇非技术快速入门题解(二)
大家好,我是RecordLiu。 初学SQL,有哪些合适的练习网站推荐呢? 如果你有编程基础,那么我推荐你到Leetcode这样的专业算法刷题网站,如果没有,也不要紧,你也可以到像牛客网一样的编程网站去练习。 牛客网有很多面向非技…...

航天器轨道六要素和TLE两行轨道数据格式
航天器轨道要素 椭圆轨道六根数指的是:半长轴aaa,离心率e,轨道倾角iii、升交点赤经Ω\OmegaΩ、近地点辐角ω\omegaω、和过近地点时刻t0t_0t0(或真近点角φ)。 决定轨道形状: 轨道半长轴aaa࿱…...

【Spring Cloud Alibaba】第01节 - 课程介绍
一、Spring Cloud Alibaba 阿里巴巴公司 以Spring Cloud的衍生微服务一站式解决方案 二、学习Spring Cloud Alibaba的原因 Spring Cloud 多项组件宣布闭源或停止维护Spring Cloud Alibaba 性能优于Spring Cloud 三、适应群体 有Java编程和SpringBoot基础,最好有Sp…...

iOS和Android手机浏览器链接打开app store或应用市场下载软件讲解
引言当开发一个app出来后,通过分享引流用户去打开/下载该app软件,不同手机下载的地方不一样,比如:ios需要到苹果商店去下载,Android手机需要到各个不同的应用商店去下载(华为手机需要到华为应用商店下载,vi…...

2023第十四届蓝桥杯省赛java B组
试题 A: 阶乘求和 本题总分:5 分 【问题描述】 令 S 1! 2! 3! ... 202320232023!,求 S 的末尾 9 位数字。 提示:答案首位不为 0。 【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数…...
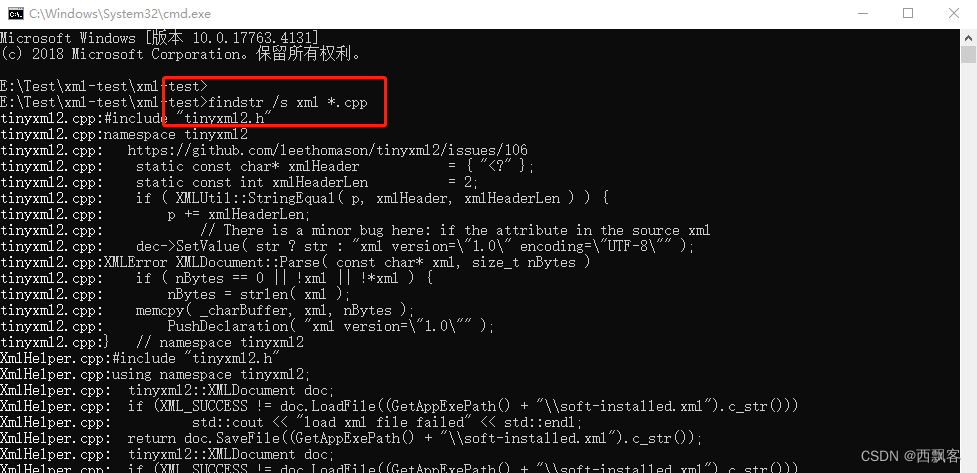
windows下如何快速搜索文件内容
安装git,使用linux命令 grep 这里不再多说 windows版本的命令 Windows提供find/findstr类似命令,其中findstr要比find功能更多一些,可以/?查看帮助。...

Redis集群分片
文章目录1、Redis集群的基本概念2、浅析集群算法-分片-槽位slot2.1 Redis集群的槽位slot2.2 Redis集群的分片2.3 两大优势2.4 如何进行slot槽位映射2.5 为什么redis集群的最大槽数是16384个?2.6 Redis集群不保证强一致性3、集群环境搭建3.1 主从容错切换迁移3.2 主从…...
)
ISP-AF相关-聚焦区域选择-清晰度评价-1(待补充)
1、镜头相关 镜头类型 变焦类型: 定焦、手动变焦、自动变焦 光圈: 固定光圈、手动光圈、自动光圈 视场角: 鱼眼镜头、超广角镜头、广角镜头、标准镜头、长焦镜头、超长焦镜头(由大至小) 光圈: 超星…...

[element-ui] el-table行添加阴影悬浮效果
问题: 在el-table每一行获得焦点与鼠标经过时,显示一个整行的阴影悬浮效果 /*其中,table-row-checkd是我自定义的焦点行添加类名,大家可以自己起名*/ .el-table tbody tr:hover,.el-table tbody tr.table-row-checked{box-shadow: 0px 3px …...
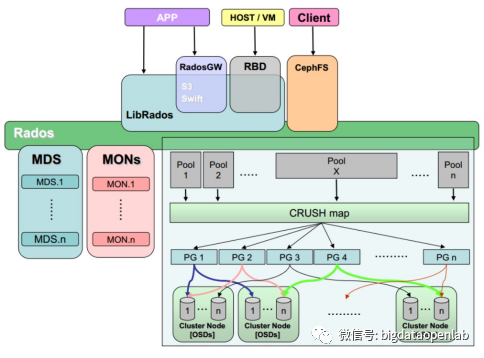
分布式存储技术(上):HDFS 与 Ceph的架构原理、特性、优缺点解析
面对企业级数据量,单机容量太小,无法存储海量的数据,这时候就需要用到多台机器存储,并统一管理分布在集群上的文件,这样就形成了分布式文件系统。HDFS是Hadoop下的分布式文件系统技术,Ceph是能处理海量非结…...

【python设计模式】20、解释器模式
哲学思想: 解释器模式(Interpreter Pattern)是一种行为型设计模式,它提供了一种方式来解释和执行特定语言的语法或表达式。该模式中,解释器通过将表达式转换为可以执行的对象来实现对表达式的解释和执行。通常…...
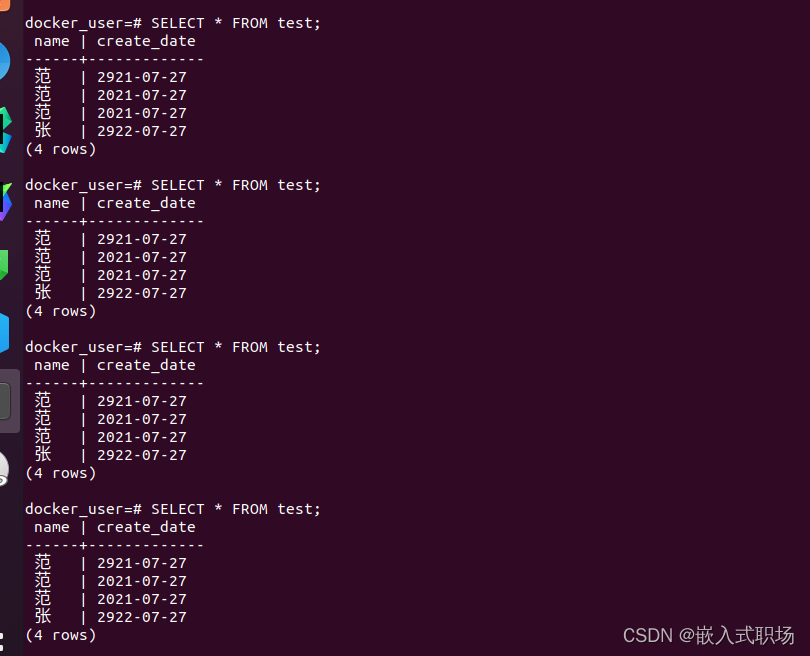
【PostgreSQL】通过docker的方式运行部署PostgreSQL与go操作数据库
目录 1、docker的方式运行部署PostgreSQL 2、控制台命令 3、go操作增删改查 1、docker的方式运行部署PostgreSQL docker pull postgres docker run --name learn_postgres -e POSTGRES_PASSWORDdocker_user -e POSTGRES_USERdocker_user -p 5433:5432 -d postgres进入容器&am…...

Kotlin协程序列:
1: 使用方式一 ,callback和coroutine相互转化。 import kotlinx.coroutines.* import java.lang.Exception class MyCallback {fun doSomething(callback: (String?, Exception?) -> Unit) {// 模拟异步操作GlobalScope.launch {try {delay(1000) // 延迟 1 秒…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
