NIO消息黏包和半包处理
1、前言
我们在进行NIO编程时,通常会使用缓冲区进行消息的通信(ByteBuffer),而缓冲区的大小是固定的。那么除非你进行自动扩容(Netty就是这么处理的),否则的话,当你的消息存进该缓冲区就会存在消息边界的问题,典型的边界问题就是黏包和半包现象。
2、什么是消息黏包?
当ByteBuffer设置足够大时,会有多条消息从channel写进ByteBuffer,这时候就无法愤青数据包的边界,所有数据包粘连在一起,称为黏包问题。
如:

3、什么是消息半包?
当数据包足够大,ByteBuffer直接被填满,但是又不包含完整的数据包。这就会导致从缓冲区中取出的消息不完整,有点像消息被“砍了一半”,称为半包问题。
如:

4、三种解决思路
4.1、固定缓冲区和数据包大小
固定缓冲区和数据包大小,顾名思义就是服务端按照预定的长度读取。数据包发送的大小和ByteBuffer固定大小填充传输,就算数据包小于ByteBuffer容量,也需要填充满。
如:

很明显这种方案的缺点就是浪费带宽。因为如果数据包有多大,就算只有1字节,剩下的也需要用多余的数据填充。
4.2、按分隔符拆分不同缓冲区
按既定的分隔符拆分(如\r,\n)。缓冲区读取按既定分隔符截取,依次判断如果是分隔符,就创建相应缓冲区进行存储。保证了分隔符前后数据不会冲突。
如:
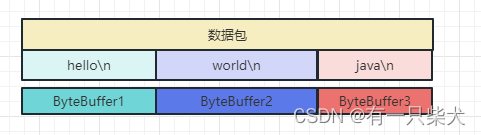
很明显这种方案有个致命问题,就是效率低。每分割一条消息就需要创建自动扩容的ByteBuffer。
参考代码:
private static void split(final ByteBuffer buffer) {buffer.flip();for(int i=0;i<buffer.limit();i++){if (buffer.get(i)=='\n') {//遇到\n,表示一个完整的语句。写入的bufferint length=i+1-buffer.position();ByteBuffer target = ByteBuffer.allocate(length);//将数据写入targetfor (int j = 0; j < target.limit(); j++) {// 将buffer中的数据写入target中target.put(buffer.get());}debugAll(target);}}//读取完毕之后读取剩余的部分,不能使用clear。clear会从头开始的buffer.compact();
}
4.3、报文头添加消息长度字段
这种方案也是最常用的方案,就是在传输的报文头添加一个固定长度的字段,用来存储当前这条消息具体数据的长度。这样当我们接收到这条报文之后,只要固定解析报文头部几个字节,就可以知道当前这条消息的长度,然后进而进行解析。
这也就是TLV格式,即 Type 类型、Length 长度、Value 数据(也就是在消息开头用一些空间存放后面数据的长度),如HTTP请求头中的Content-Type与Content-Length。类型和长度已知的情况下,就可以方便获取消息大小,分配合适的 buffer,缺点是 buffer 需要提前分配,如果内容过大,则影响 server 吞吐量。
- Http 1.1 是TLV格式
- Http 2.0 是LTV格式
如以下的http请求响应头,便可以看到Content-Length:121。这就是消息具体数据的长度。
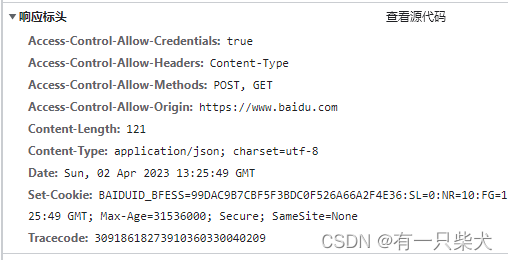
如:

或
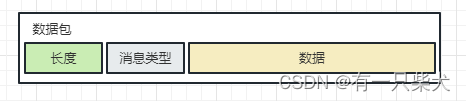
相关文章:

NIO消息黏包和半包处理
1、前言 我们在进行NIO编程时,通常会使用缓冲区进行消息的通信(ByteBuffer),而缓冲区的大小是固定的。那么除非你进行自动扩容(Netty就是这么处理的),否则的话,当你的消息存进该缓冲…...

day018 第六章 二叉树 part05
一、513.找树左下角的值 这个题目的主要思路是使用广度优先搜索(BFS)遍历整棵树,最后返回最后一层的最左边的节点的值。具体的实现可以使用队列来存储每一层的节点,并且在遍历每一层节点时,不断更新最左边的节点的值。…...
如何下载ChatGPT-ChatGPT如何写作
CHATGPT能否改一下文章 ChatGPT 作为一种自然语言处理技术,生成的文章可能存在表达不够准确或文风不符合要求等问题。在这种情况下,可以使用编辑和修改来改变输出的文章,使其符合特定的要求和期望。 具体来说,可以采用以下步骤对…...

微策略再次买入
原创:刘教链* * *隔夜,比特币再次小幅回升至28k上方。微策略(Microstrategy)创始人Michael Saylor发推表示,微策略再次出手,买入1045枚比特币。此次买入大概花费2930万美元,平均加仓成本28016美…...

express框架
Express 是基于 Node.js 平台,快速、开放、极简的 Web 开发框架. 创建一个基本的express web服务器 // 1.导入express const express require(express); // 2.创建web服务器 const app express(); // 3.启动web服务器 app.listen(80, ()>{console.log(expres…...

完蛋的goals
...

Javase学习文档------面象对象初探
引入面向对象 面向对象的由来: 面向对象编程(Object-Oriented Programming, OOP)是一种编程范型,其由来可以追溯到20世纪60年代。在此之前,主流编程语言采用的是“过程化编程”模式,即面向过程编程模式。在这种模式下&…...

ChatGPT能够干翻谷歌吗?
目前大多数人对于ChatGPT的喜爱,主要源自于其强大的沟通能力,当我们向ChatGPT提出问题时,它不仅能够为我们提供结论,而且还能够与我们建立沟通,向ChatGPT提出任何问题,感觉都像是在与一个真实的人类进行交谈…...

PCL 使用点云创建数字高程模型DEM
目录 一、DEM1、数字高程模型二、代码实现三、结果展示1、点云2、DEM四、相关链接一、DEM 1、数字高程模型 数字高程模型(Digital Elevation Model),简称DEM,是通过有限的地形高程数据实现对地面地形的数字化模拟(即地形表面形态的数字化表达),它是用一组有序数值阵列形…...
我体验了首个接入GPT-4的代码编辑器,太炸裂了
最近一款名为Cursor的代码编辑器已经传遍了圈内,受到众多编程爱好者的追捧。 它主打的亮点就是,通过 GPT-4 来辅助你编程,完成 AI 智能生成代码、修改 Bug、生成测试等操作。 确实很吸引人,而且貌似也能大大节省人为的重复工作&…...
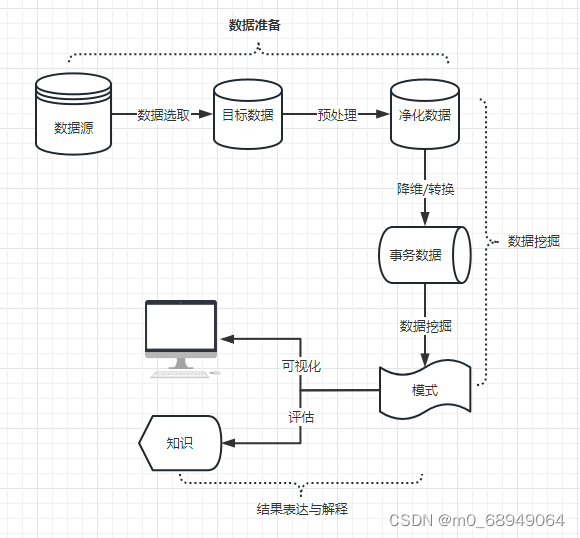
互联网数据挖掘与分析讲解
一、定义 数据挖掘(英语:Data mining),又译为资料探勘、数据采矿。它是数据库知识发现(英语:Knowledge-Discovery in Databases,简称:KDD)中的一个步骤。数据挖掘一般是指从大量的数…...

linux之cut的使用
cut是一个选取命令,就是将一段数据经过分析,取出我们想要的。一般来说,选取信息通常是针对“行”来进行分析的,并不是整篇信息分析的 其语法格式为: cut [-bn] [file] 或 cut [-c][file] 或 cut [-df] [file]使用说明:…...
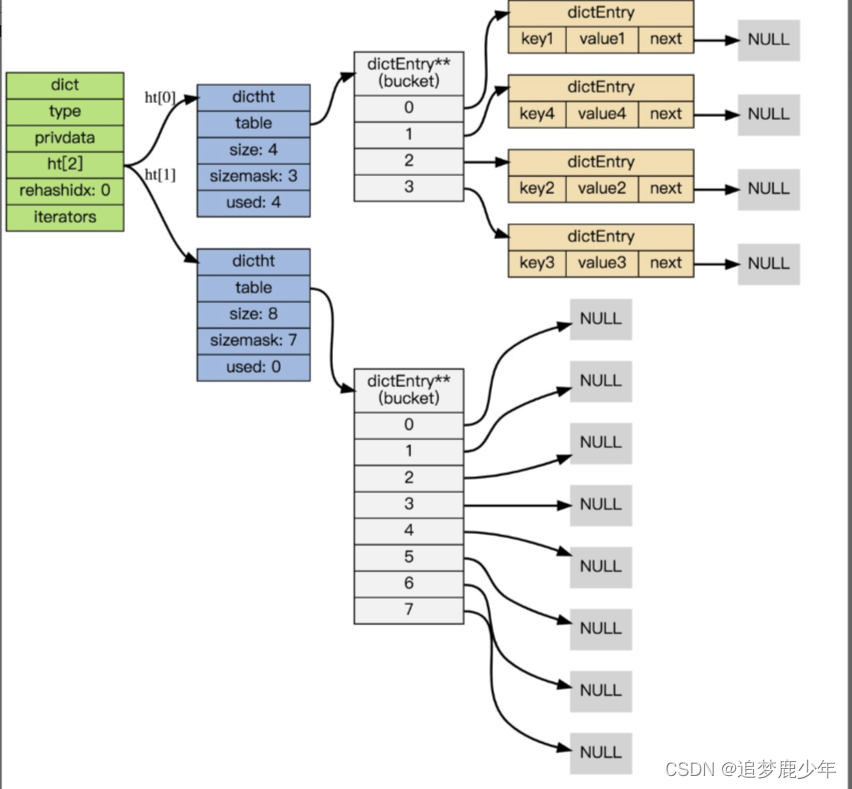
Redis第十讲 Redis之Hash数据结构Dict-rehash扩容操作
Rehash 执行过程 字典的 rehash 操作实际上就是执行以下任务: 创建一个比 ht[0]->table 更大的 ht[1]->table ;将 ht[0]->table 中的所有键值对迁移到 ht[1]->table ;将原有 ht[0] 的数据清空,并将 ht[1] 替换为新的 ht[0] ; 经过以上步骤之后, 程序就在不改…...
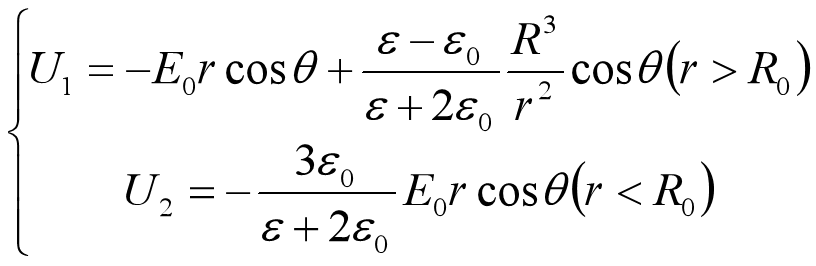
电动力学问题中的Matlab可视化
电磁场的经典描述 小说一则 电磁场的经典描述就是没有啥玩意量子力学的经典电动力学下对电磁场的描述,以后有空写个科幻小说,写啥呢,就写有天张三遇见了一个外星人,外星人来自这样一个星球,星球上的物质密度特别低,导致外星人的测量会明显的影响物质的运动,外星人不能同时得到…...

云原生周刊:编程即将终结?
近日哈佛大学计算机科学的前教授 Matt Welsh,分享了他对计算机科学、分布式计算的未来以及 ChatGPT 和 GitHub Copilot 是否代表编程结束的开始的看法。 威尔士说,编程语言仍然很复杂。再多的工作也无法让它变得简单。 “在我看来,任何改进…...

C++ STL,resize 和 reserve 的区别
结论放前边:resize和reserve都可以给容器扩容,区别在于resize会进行填充,使容器处于满员的状态,即sizecapacity,而reserve不会填充,有size<capacity. 1. size 和 capacity 的区别 size和capacity是容器…...

Java——详解ReentrantLock与AQS的关联以及AQS的数据结构和同步状态State
前言 Java中大部分同步类(Lock、Semaphore、ReentrantLock等)都是基于AbstractQueuedSynchronizer(简称为 AQS)实现的。 AQS 是一种提供了原子式管理同步状态、阻塞和唤醒线程功能以及队列模型的简单框架。 本文会先介绍应用层&a…...

vue3+vite+ts 接入QQ登录
说明 前提资料准备 在QQ互联中心注册成为开发者 站点:https://connect.qq.com/创建应用,如图 js sdk方式 下载对应的sdk包 sdk下载:https://wiki.connect.qq.com/sdk%e4%b8%8b%e8%bd%bd 使用 下载离线js sdk 打开:https:…...
消息队列kafka及zookeeper机制
目录 一、zookeeper 1、zookeeper简介 2、zookeeper特点 3、zookeeper工作模式及机制 4、zookeeper应用场景及选举机制 5、zookeeper集群部署 ①实验环境 ②安装zookeeper 二、消息队列kafka 1、为什么要有消息队列 2、使用消息队列的好处 3、kafka简介 4、kafka…...
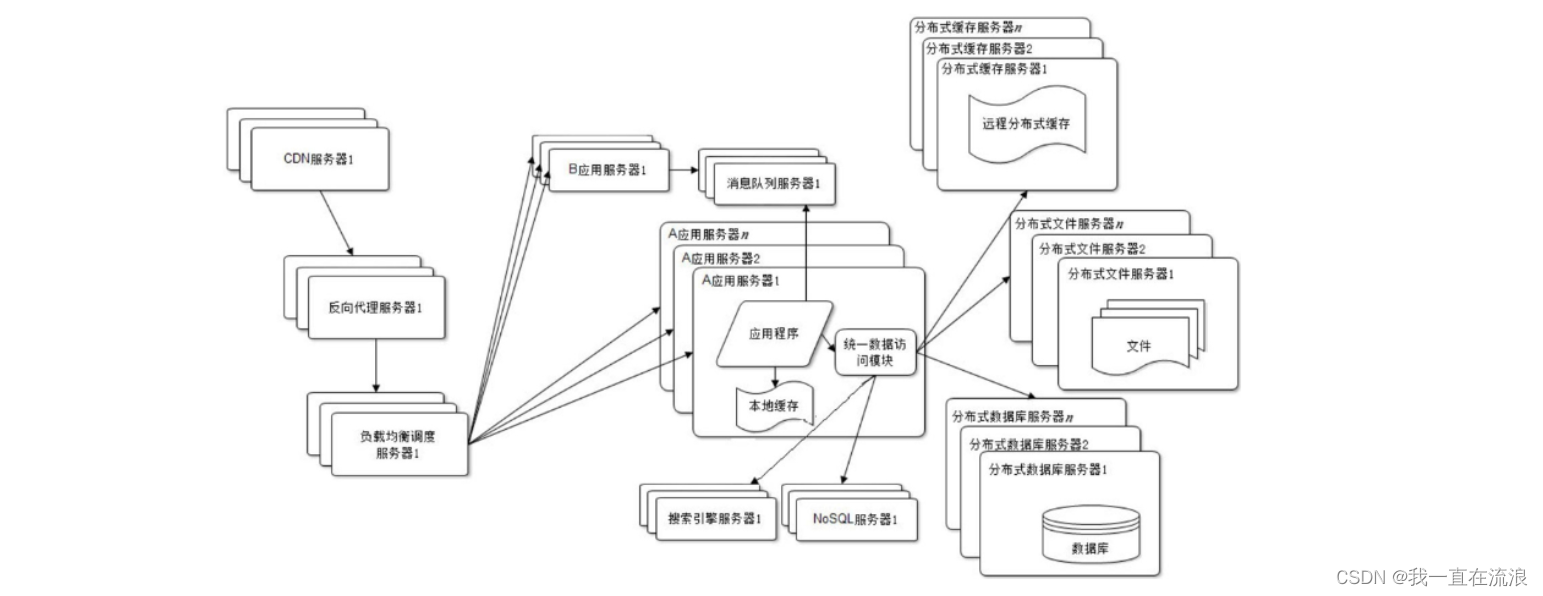
分布式 - 分布式体系架构:IT架构的演进过程
文章目录01. 应用与数据一体模式02. 应用服务和数据服务的分离03. 缓存与性能的提升04. 服务器集群处理并发05. 数据库读写分离06. 反向代理和 CDN07. 分布式文件系统和分布式数据库系统08. NoSQL和搜索引擎09. 业务拆分10. Redis缓存在应用服务器上是进程内缓存还是进程外缓存…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
