代码随想录算法训练营第五十六天 | 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结
583. 两个字符串的删除操作
动规五部曲
1、确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
2、确定递推公式
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么在删 word1[i - 1],就达到了两个元素都删除的效果,即 dp[i][j-1] + 1
3、dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
4、确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
5、举例推导dp数组
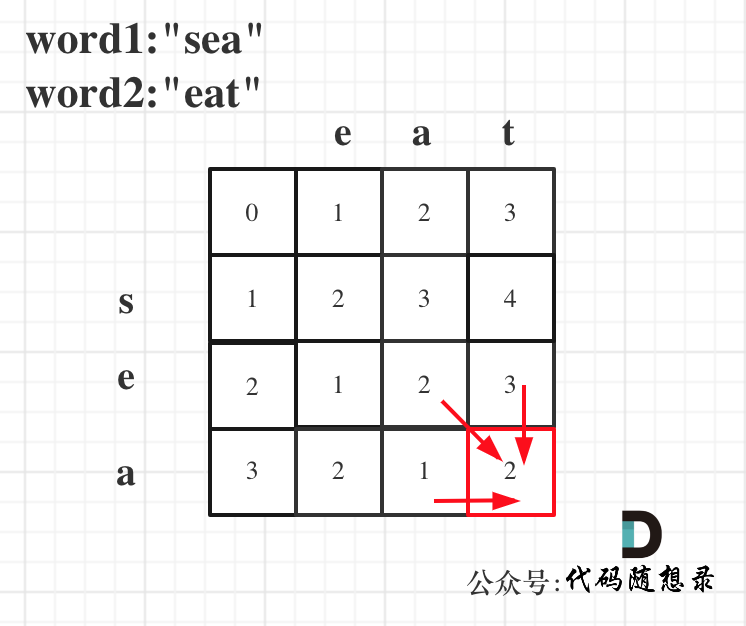
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp[word1.size()][word2.size()];}
};思路二
只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return word1.size() + word2.size() - dp[word1.size()][word2.size()] * 2;}
};72. 编辑距离
动规五部曲
1、确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
2、确定递推公式
在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])不操作
if (word1[i - 1] != word2[j - 1])增删换if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1])
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad"
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
3、dp数组如何初始化
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
4、确定遍历顺序
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:

所以在dp矩阵中一定是从左到右从上到下去遍历。
5、举例推导dp数组
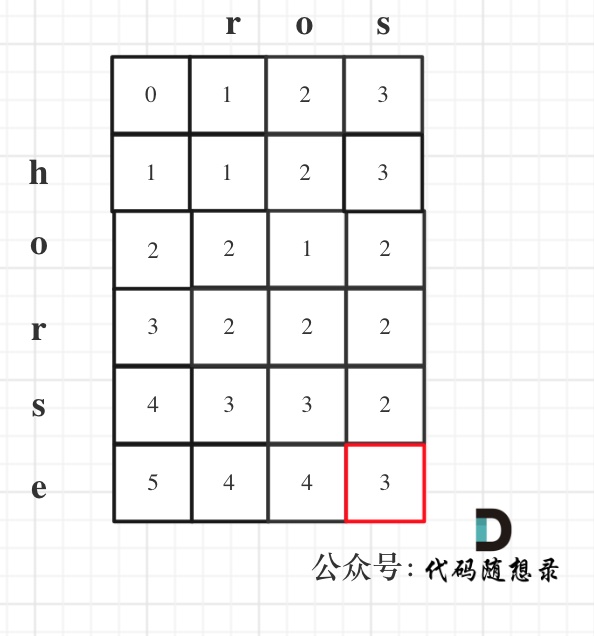
以示例1为例,输入:word1 = "horse", word2 = "ros"为例,dp矩阵状态图如下:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;}}}return dp[word1.size()][word2.size()];}
};
编辑距离总结
编辑距离从判断子序列->判断子序列 ->不同的子序列 ->两个字符串的删除操作->编辑距离
以上四个题都是从最初子序列开始,在原本一个子序列的基础上,变成了二维,通过观察每次解题代码可以发现,其实各题在解题思路上都几乎类似,难点在于递推公式的推导与初始化,递推公式的推导要在理解各题要求的同时,思考该如何得出当前状态,时刻谨记dp数组的定义有利于递推公式推导
相关文章:

代码随想录算法训练营第五十六天 | 583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结
583. 两个字符串的删除操作 动规五部曲 1、确定dp数组(dp table)以及下标的含义 dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。 2、确定递推…...
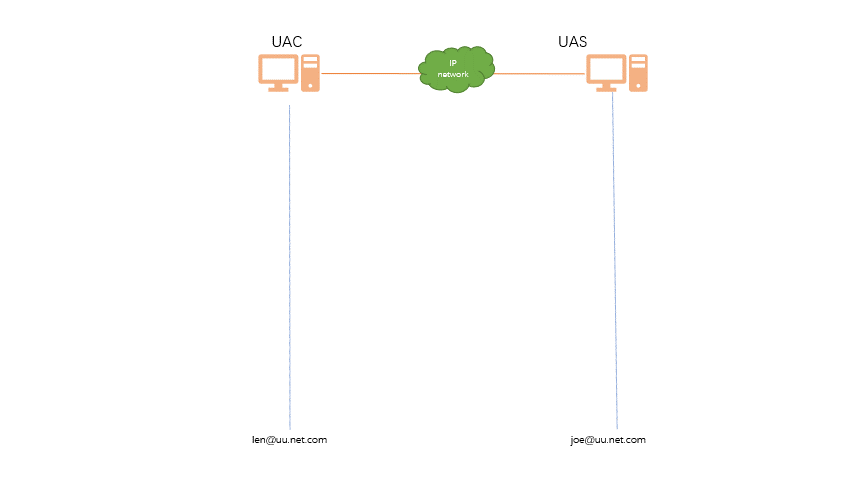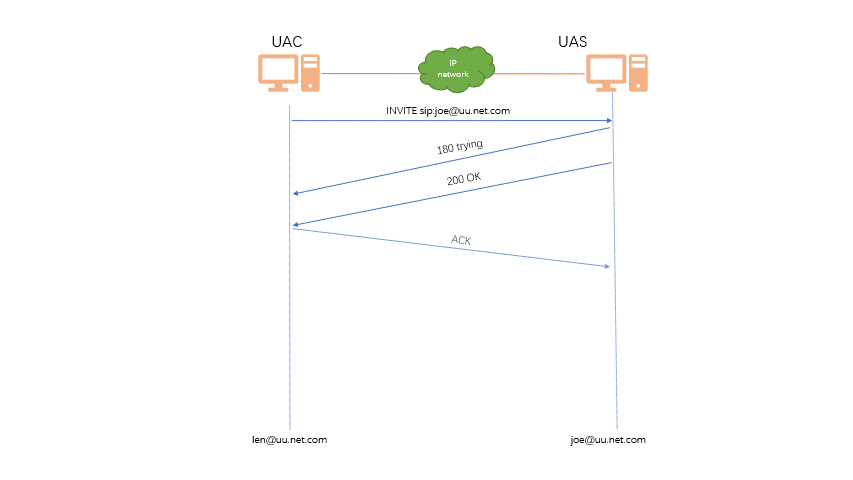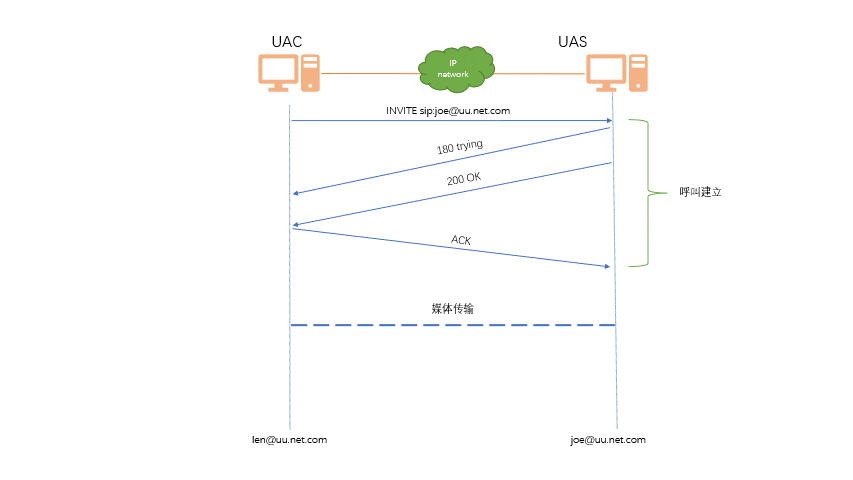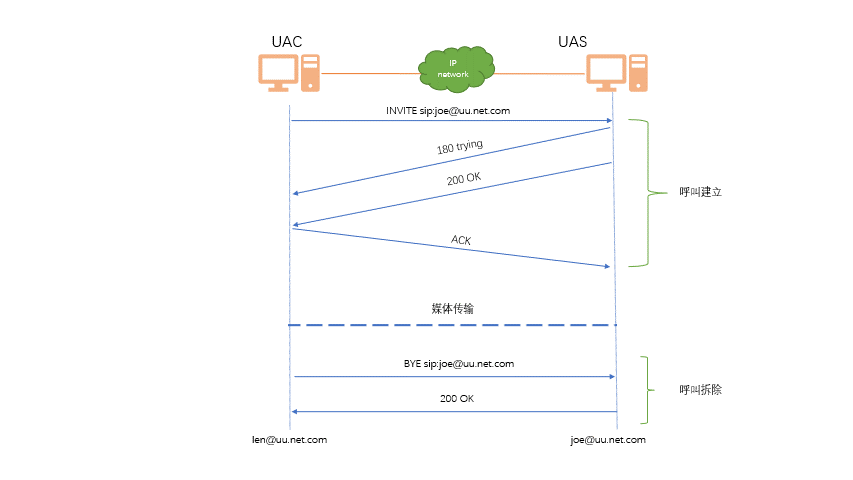
Sip协议
简介 SIP(Session Initiation Protocol,会话初始协议)是一个用于建立、更改和终止多媒体会话的应用 层控制协议,其中的会话可以是 IP 电话、多媒体会话或多媒体会议。SIP 是 IETF 多媒体数据和控 制体系结构的核心协议࿰…...

RandomAccessFile类 断点续传
文章目录学习链接RandomAccessFile构造方法实现的接口DataOutputDataInputAutoCloseable重要的方法多线程读写同一个文件(多线程复制文件)代码1代码2断点续传FileUtils学习链接 RandomAccessFile详解 Java IO——RandomAccessFile类详解 java多线程-断点…...

SpringCloud微服务技术栈的注册中心Eureka
文章目录SpringCloud微服务技术栈的注册中心Eureka简介Eureka特点操作步骤环境准备创建Eureka Server注册服务提供方调用服务消费方总结SpringCloud微服务技术栈的注册中心Eureka 简介 在微服务架构中,服务的数量庞大,而且每个服务可能会有多个实例。此…...

Unity最新热更新框架 hybridclr_addressable
GitHub:YMoonRiver/hybridclr_addressable: 开箱即用的商业游戏框架,集成了主流的开发工具。将主流的GameFramework修改,支持Addressable和AssetBundle,已完善打包工具和流程。 (github.com) # 新增GameFramework Addressables 开箱即用 # 新…...
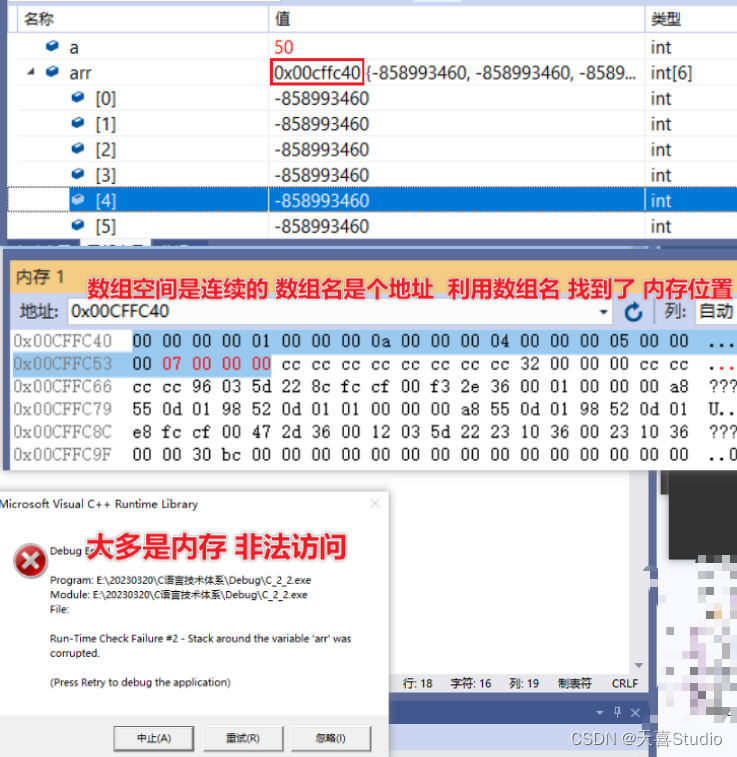
【c语言】一维数组***特性、存储原理
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
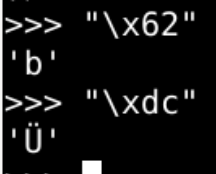
[oeasy]python0133_[趣味拓展]好玩的unicode字符_另类字符_上下颠倒英文字符
另类字符 回忆上次内容 上次再次输出了大红心♥ 找到了红心对应的编码黑红梅方都对应有编码 原来的编码叫做 ascii️ \u这种新的编码方式叫unicode包括了 中日韩字符集等 各书写系统的字符集 除了这些常规字符之外 还有什么好玩的东西呢? 颠倒字符 这个网站可以…...

找凶手,定名次,字符串旋转,杨氏矩阵
1.找凶手问题: //题目名称: //猜凶手 //题目内容: //日本某地发生了一件谋杀案,警察通过排查确定凶手必为4个嫌疑犯的一个。 //以下为4个嫌疑犯的供词: //A说:不是我 //B说:是C //C说ÿ…...

Python 进阶指南(编程轻松进阶):十四、实践项目
原文:http://inventwithpython.com/beyond/chapter14.html 到目前为止,这本书已经教会了你编写可读的 Python 风格代码的技巧。让我们通过查看两个命令行游戏的源代码来实践这些技术:汉诺塔和四人一排。 这些项目很短,并且基于文…...

Redis的五种数据类型及应用场景
Redis是一个开源的key-value数据库。 五种数据类型 String,List, Set,SortedSet,Hash List类型可以存储多个String。 Set类型可以存储不同的String。 SortedSet可以存储String的排序。 Hash可以存储多个key-value对。 String …...

c++List的详细介绍
cList详细使用 write in front 作者: 不进大厂不改名 专栏: c 作者简介:大一学生 希望能向其他大佬和同学学习! 本篇博客简介:本文主要讲述了一种新容器list的使用方法,相信你在学了后,能够加深…...
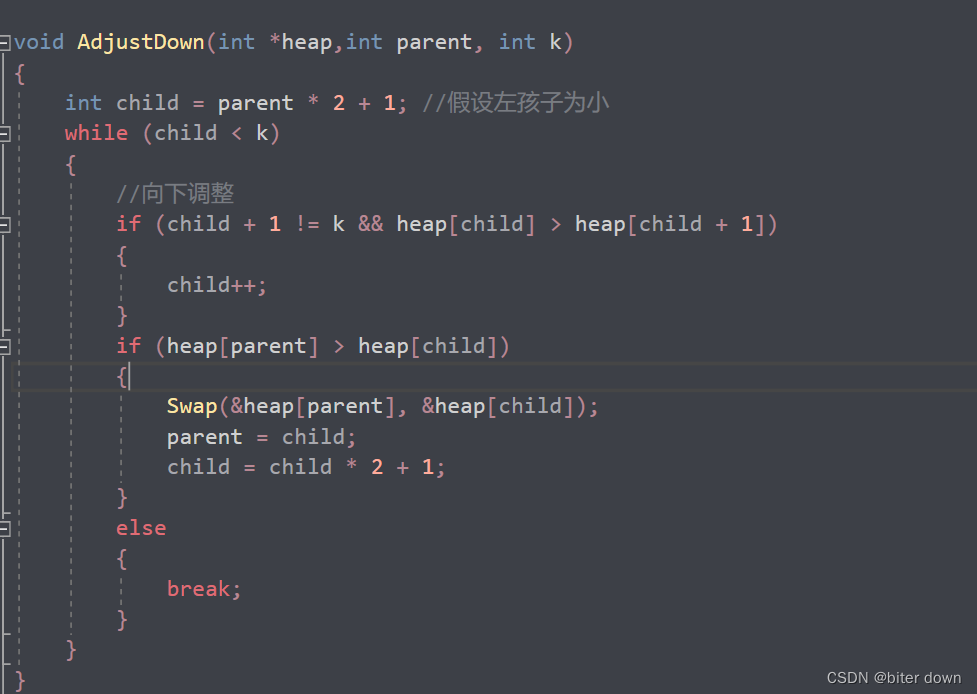
Heap堆的升序排序
在heap堆中,大根堆是一种特殊的堆,它满足下列性质:对于任意一个非叶子节点i,其左右子节点的值均小于等于它本身的值。 在大根堆中,堆顶元素永远是值最大的元素,所以将堆顶元素不断取出来,就相当…...
小程序开发收费价目表
小程序作为一种新兴应用形式,正在逐渐成为企业和个人推广、运营的重要手段。然而,小程序开发的价格因项目规模和复杂程度差异较大,令不少人望而却步。本文将从小程序开发的相关因素入手,探讨小程序开发的价格范围和算法。 一、小…...

Dubbo服务暴露步骤详解
文章目录Dubbo服务暴露步骤详解背景介绍理论知识讲解什么是服务暴露?Dubbo 服务暴露的基本原理操作步骤具体实现环境准备实现服务接口实现服务提供者配置 Dubbo 服务提供者启动服务提供者实现服务消费者配置 Dubbo 服务消费者测试总结Dubbo服务暴露步骤详解 背景介…...

第十四届蓝桥杯编程题部分代码题解
C. 冶炼金属 最大值就是取 a/ba / ba/b 的最小值,最小值就是二分找到满足 mid∗(bi1)≥aimid * (b_i 1) ≥ a_imid∗(bi1)≥ai 的最小值 #include<bits/stdc.h> #define int long long #define x first #define y second using namespace std;void sol…...
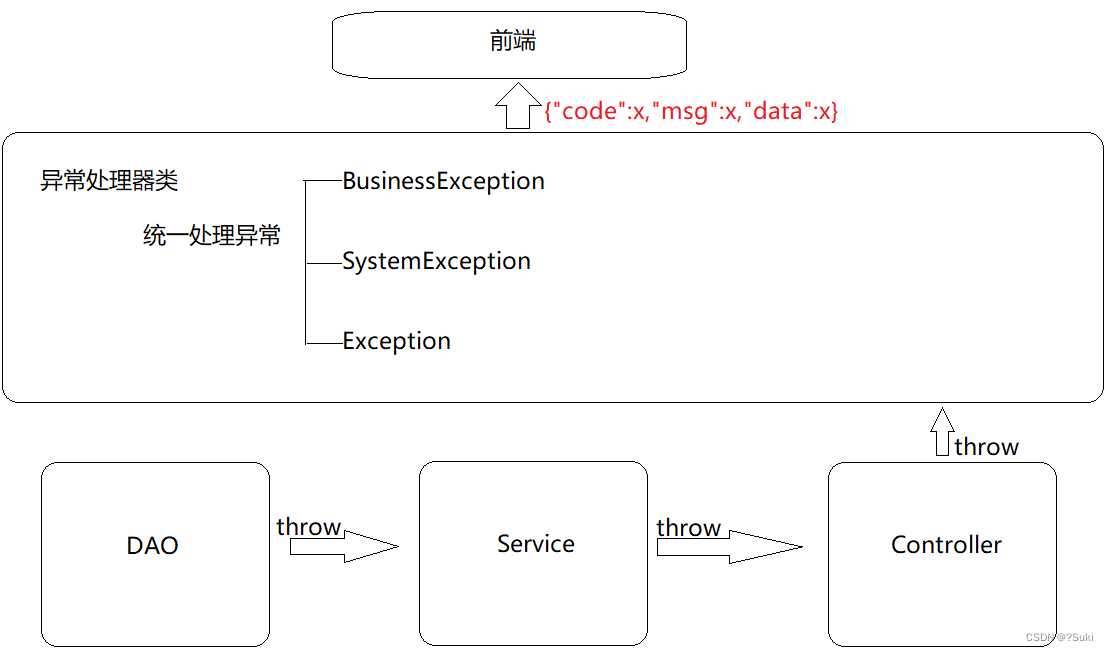
统一结果封装异常处理
统一结果封装&异常处理2,统一结果封装2.1 表现层与前端数据传输协议定义2.2 表现层与前端数据传输协议实现2.2.1 环境准备2.2.2 结果封装步骤1:创建Result类步骤2:定义返回码Code类步骤3:修改Controller类的返回值步骤4:启动服务测试3,统一异常处理3…...

数字藏品平台的发展趋势是什么?
1、数字藏品平台具体内容生产模式将在PGC(专业生产制造具体内容)方式向PUGC(技术专业用户生产内容)方式变化。 目前,中国热门的数字藏品平台都在PGC模式中持续发展的,而国外流行NFT平台则比较多选用UGC&am…...
Vue3对话框(Dialog)
Vue2对话框(Dialog) 可自定义设置以下属性: 标题(title),类型:string | slot,默认 提示 内容(content),类型:string | slot…...

【深度强化学习】(5) DDPG 模型解析,附Pytorch完整代码
大家好,今天和各位分享一下深度确定性策略梯度算法 (Deterministic Policy Gradient,DDPG)。并基于 OpenAI 的 gym 环境完成一个小游戏。完整代码在我的 GitHub 中获得: https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Mod…...

unity,Color.Lerp函数
介绍 Color.Lerp函数是Unity引擎中的一个静态函数,用于在两个颜色值之间进行线性插值,从而实现颜色渐变效果 方法 Color.Lerp函数是Unity引擎中的一个静态函数,用于在两个颜色值之间进行线性插值,从而实现颜色渐变效果。该函数的…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
