软件设计(十一)数据结构(上)
- 线性结构
- 线性表
线性表是n个元素的有限序列,通常记为(a1,a2....an),特点如下。
- 存在唯一的一个称作“第一个”的元素。
- 存在位移的一个称作“最后一个”的元素。
- 除了表头外,表中的每一个元素均只有唯一的直接前趋
- 除了表尾外,表中的每一个元素均只有唯一的直接后继
1)线性表的 顺序存储:优点随机存取表中元素,缺点每次插入需要移动大量元素。
2)线性表的 链式存储:指用节点来存储数据元素,节点的空间可以是连续的,也可以是不连续的,因此存储数据元素的同时必须存储元素之间的逻辑关系。节点空间只有在需要的时候才申请,无须事先分配。
链表作为存储结构时,不能进行数据元素随机访问,但优点是插入和删除操作时候不需要移动大量数据。
常用的链表结构:
- 双向链表:每个节点包含两个指针,指明直接前趋和后继,可在两个方向遍历链表。
- 循环链表:表尾的指针指向第一个节点。
- 静态链表:借助数组来描述线性表的链式存储结构。
- 栈和队列
栈
只能通过访问它一端来实现数据存储和检索的一种线性数据结构。它是先进后出的原则FILO。
栈典型的应用包括表达式求值、括号匹配等。在计算机语言的实现以及将递归过程转变为非递归过程的处理中,栈都很重要
队列
队列是一种先进先出(FIFO)的线性表,它只允许在表的一端插入元素,表的另一端删除元素。
- 数组、矩阵和广义表
- 数组
n维数组是一种“同构”的数据结构,其每一个元素类型相同,结构一致。数组是定长线性表在维数上的扩张,即线性表中的元素又是一个线性表。
数组结构特点:数据元素数目固定、数据元素具有相同的类型、数据元素的下标关系具有上下界的约束且下标有序。
一旦定义了数组,结构中元素个数和元素之间的关系就不再发生改变,因此数组适用于采用顺序存储结构。
因为计算机内存结构是一维线性的,因此存储多维数组时必须按照某种方式进行降维处理。
- 矩阵
特殊矩阵:若矩阵中元素(或非0元素)的分部有一定规律,则为特殊矩阵。(如 三角矩阵、对称矩阵、对角矩阵)
稀疏矩阵:若非零的元素远远小于零元素的个数,且非零元素的分部没有规律,则为稀疏矩阵。
- 广义表
广义表是线性表的推广,由0个或者多个单元素或子表所组成的有限序列。
广义表长度是元素的个数,深度指广义表展开后所含括号的最大层数。
- 树
树是n(n>=0)个节点的有限集合,n=0时称为空树,在任意非空树中:
- 有且仅有一个称为根的节点。
- 其余的节点可分为m(m>=0)个互不相交的子集T1,T2...Tm,其中每个子集本身又是一棵树,并称为根节点的子树。
树由若干子树构成,子树又由子树构成。
- 双亲和孩子:节点的子树的跟称为该节点的孩子,该节点称为其子节点的双亲。
- 兄弟:具有相同双亲的节点互为兄弟。
- 节点的度:一个节点的子树的个数记为该节点的度。
- 叶子结点:也称为终端节点,指度为0的节点。
等...
- 二叉树
二叉树binary tree是n(n>=0)个节点的有限集合,它或者是空树(n=0),或者是由一个根节点及两棵互不相交的、分别称为左子树和右子树的二叉树所组成。
二叉树节点最大度为2,而普通树不限制节点的度数。
二叉树基本运算时是遍历,他有如下性质:
- 二叉树第i层上的节点数目最多为 2 的 (i-1)次方。(i>=1)
- 深度为k的二叉树至多 (2的k次方)-1 个节点。(i>=1)
- 在任意一颗二叉树中,若终端节点数为n0,度为2的节点数为n2,则n0 = n2+1。
等...
二叉树的遍历
二叉树分为根节点、左子树和右子树,按照左子树必须遍历在右子树之前,所以分为前序、中序、后续。
也可以层序遍历,从树的根节点出发,依次访问第一层节点,从左往右依次访问第二层的节点,以此类推,自上而下,自左往右。
- 图
图G是由两个集合V和E构成的二元组,记作G=(V,E),其中V是图中顶点的非空有限集合,E是图中边的有限集合。从数据结构逻辑关系看,图中任意顶点都与其他顶点有关,而图中所有顶点都有可能与某一顶点有关。在图中,数据结构中的数据元素用顶点表示,数据元素之间的关系则用边表示。
- 有向图:若图中每条边都是有方向的,则称G为有向图。
- 无向图:若图中每一条边都是无方向的。
- 无向完全图:若一个图像图具有n个顶点,若每一个顶点与其他n-1个顶点之间都有边,则称为无向完全图。显然含n个顶点的无向完全图共有n(n-1)/2条边。
- 有向完全图:有n个顶点的有向完全图中孤的数目为n(n-1),即任何两个不同顶点之间都有方向相反的两条弧存在。
等...
图的遍历分为:
- 深度优化遍历 DFS:从图G任意一个顶点v出发。设计搜索指针,指向旁边未访问的顶点。
- 广度优化遍历:BFS:从顶点v出发,访问v旁边都未访问过的顶点。
相关文章:
数据结构(上))
软件设计(十一)数据结构(上)
线性结构 线性表 线性表是n个元素的有限序列,通常记为(a1,a2....an),特点如下。 存在唯一的一个称作“第一个”的元素。存在位移的一个称作“最后一个”的元素。除了表头外,表中的每一个元素均只有唯一的直接前趋除了表尾外&…...
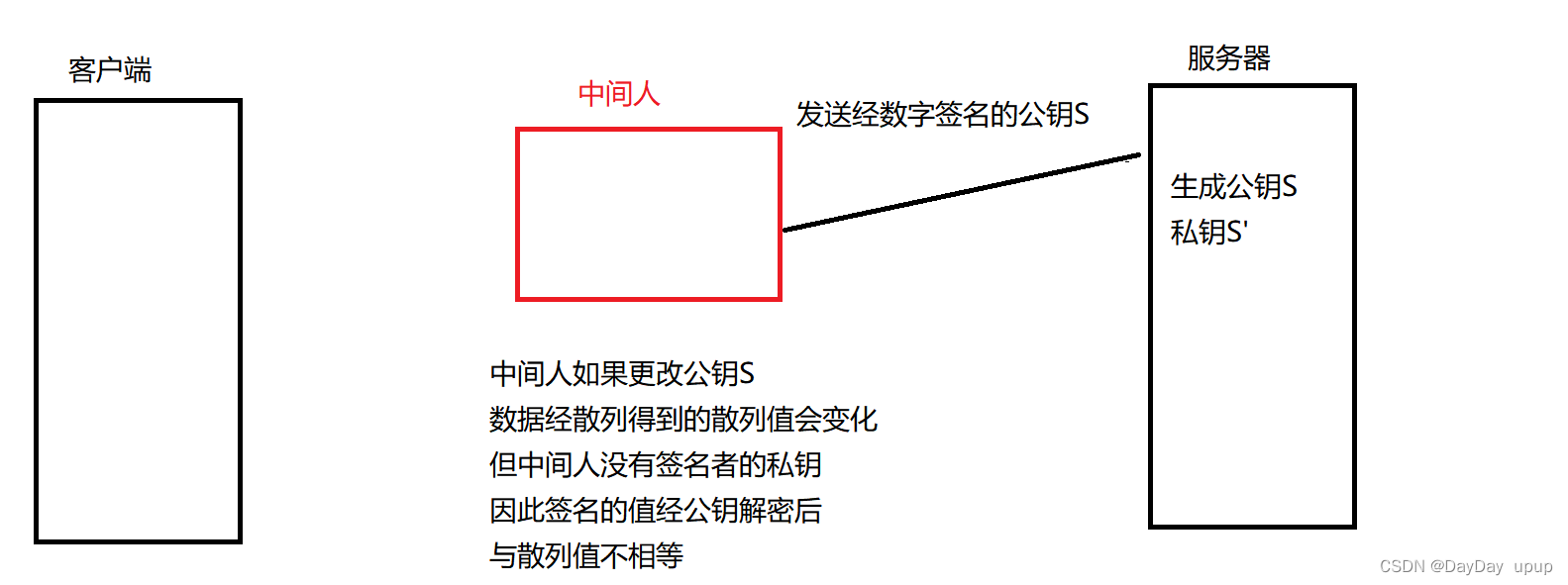
https协议
文章目录对称加密方案非对称加密方案对称加密方案非对称加密方案对称加密方案非对称加密方案数字证书因为HTTP是明文传输,所以会很有可能产生中间人攻击(获取并篡改传输在客户端及服务端的信息并不被人发觉),HTTPS加密应运而生。 …...
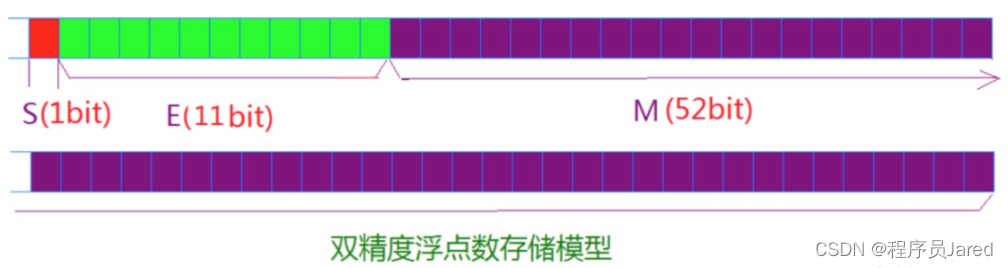
深入浅出C语言——数据在内存中的存储
文章目录一、数据类型详细介绍1. C语言中的内置类型2. 类型的基本归类:二. 整形在内存中的存储1. 原码、反码、补码2. 大小端三.浮点数存储规则一、数据类型详细介绍 1. C语言中的内置类型 C语言的内置类型有char、short、int、long、long long、float、double&…...

在 Centos 上在线安装 GitLab
作为程序员,其中一个愿望是拥有一个自己的代码存储库。在支持私有部署的代码存储库产品中,GitLab 是比较著名的了,所以今天我总结了一下在 Centos 上安装 GitLab 的过程。 依赖 基础依赖 首先,需要安装部分基础的依赖ÿ…...

模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。 1. Shapley值理论 Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免…...

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

常见的EMC问题
电磁兼容设计的目的就在于满足产品功能要求、减少调试时间,使产品满足电磁兼容标准的要求,并且使产品不会对系统中的其它设备产生电磁干扰。 电磁兼容设计中常见的问题有哪些? 1、电磁兼容设计可以从电路设计(包括器件选择&…...

Redis内存存储效率问题
目录 内存碎片是如何形成的? 如何判断是否有内存碎片? 如何清理内存碎片? INFO命令 面向 Prometheus 的 Redis-exporter 监控 实习期间,了解到,企业级开发中多个项目使用Redis,运行Redis实例的有可能是…...
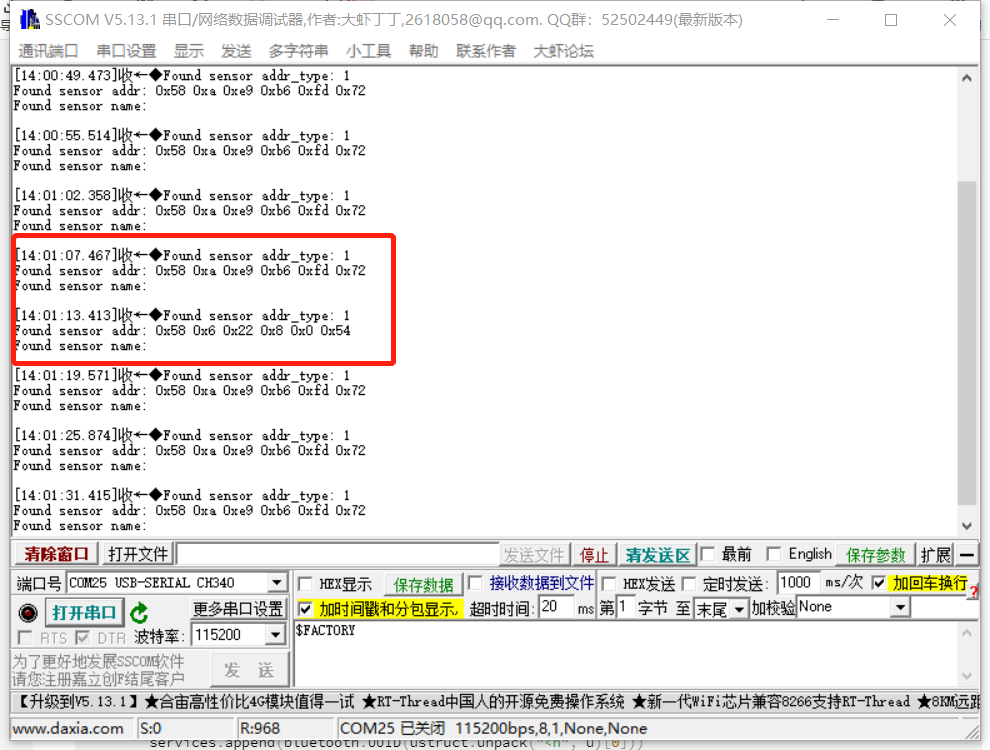
3.28 haas506 2.0开发教程-example-蓝牙多设备扫描(仅支持M320,HD1)
haas506 2.0开发教程-example-蓝牙多设备扫描案例说明蓝牙信息克隆1.手机蓝牙改名信息克隆代码测试案例说明 开发板扫描蓝牙设备,获取并打印蓝牙设备mac地址。mac地址每个设备不同,且不能更改。本案例仅适用于M320开发板和HD1-RTU。案例使用手机与iBeac…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
