焕新启航,「龙蜥大讲堂」2023 年度招募来了!13 场技术分享先睹为快
龙蜥大讲堂是龙蜥推出的系列技术直播活动,邀请龙蜥社区的开发者们分享围绕龙蜥技术展开,包括但不限于内核、编译器、机密计算、容器、储存等相关技术领域。欢迎社区开发者们积极参与,共享技术盛宴。
往期回顾
龙蜥社区技术系列直播截至目前已举办 61 场直播活动,通过钉钉、视频号、B 站平台进行直播,邀请了来自 Arm、阿里云、Intel、浪潮信息、移动、联通、普华基础软件、海光、统信软件、龙芯、飞腾、中科方德、鉴释等公司的开发者进行技术分享。
龙蜥大讲堂覆盖了今日头条、B 站、InfoQ 、CSDN、 51CTO 等多媒体矩阵,吸引了众多开发者和技术爱好者观看,在 51CTO、InfoQ 等媒体渠道播放量均达 2000+,其中镜像集群 SIG 分享视频在传播矩阵中播放量包揽 TOP 5。
焕新启航
过去,「龙蜥大讲堂」为大家带来了众多高质量多领域的技术演讲。新年伊始,为了让各位开发者和技术爱好者有更极致的、沉浸式的观看体验,对龙蜥技术有系统且全面的了解,自 2023 年 2 月开始,「龙蜥大讲堂」实现全新改版,以月度主题形式开展当月分享。 如 2 月分享主题为 SysOM 一站式系统迁移运维平台。让我们整个二月一起徜徉在 SysOM 的海洋中吧~

注意:在当月中上旬更新下一月度的演讲主题,并推送至社区官网,请各位感兴趣的技术同学及时关注并报名。
嘉宾招募
3 月分享主题方向——机密计算,比如海光 CSV、AMD SEV、Intel TDX、Intel SGX 等,欢迎小伙伴们报名分享。
报名链接:https://openanolis.mikecrm.com/XlfyCKH
若有任何疑问,欢迎添加龙蜥助手-小龙微信【openanolis_assis】咨询,龙蜥大讲堂详细资料关注龙蜥公众号【OpenAnolis龙蜥】,回复关键字“操作指南”即可获取。
往期全部资料
课件地址:
关注微信公众号(OpenAnolis),回复“龙蜥课件” 即可获取。
视频回放:https://openanolis.cn/video/
下期直播预告
今天(2023.2.13),社区邀请了系统运维 SIG Contributor 李晔分享《龙蜥自动化运维平台 SysOM 2.0 的操作系统迁移功能介绍》,带大家继续了解 SysOM 2.0 中操作系统迁移的功能设计,操作方法和问题排查等。快来扫描上面海报二维码入群,预定前排小板凳观看直播!
相关文章:

焕新启航,「龙蜥大讲堂」2023 年度招募来了!13 场技术分享先睹为快
龙蜥大讲堂是龙蜥推出的系列技术直播活动,邀请龙蜥社区的开发者们分享围绕龙蜥技术展开,包括但不限于内核、编译器、机密计算、容器、储存等相关技术领域。欢迎社区开发者们积极参与,共享技术盛宴。往期回顾龙蜥社区技术系列直播截至目前已举…...
推广传单制作工具
临近节日如何制作推广活动呢?没有素材制作满减活动宣传单怎么办?小编教你如何使用在线设计工具乔拓云,轻松设计商品的专属满减活动宣传单,不仅设计简单,还能自动生成活动分享链接,只需跟着小编下面的设计步…...
数据结构(上))
软件设计(十一)数据结构(上)
线性结构 线性表 线性表是n个元素的有限序列,通常记为(a1,a2....an),特点如下。 存在唯一的一个称作“第一个”的元素。存在位移的一个称作“最后一个”的元素。除了表头外,表中的每一个元素均只有唯一的直接前趋除了表尾外&…...
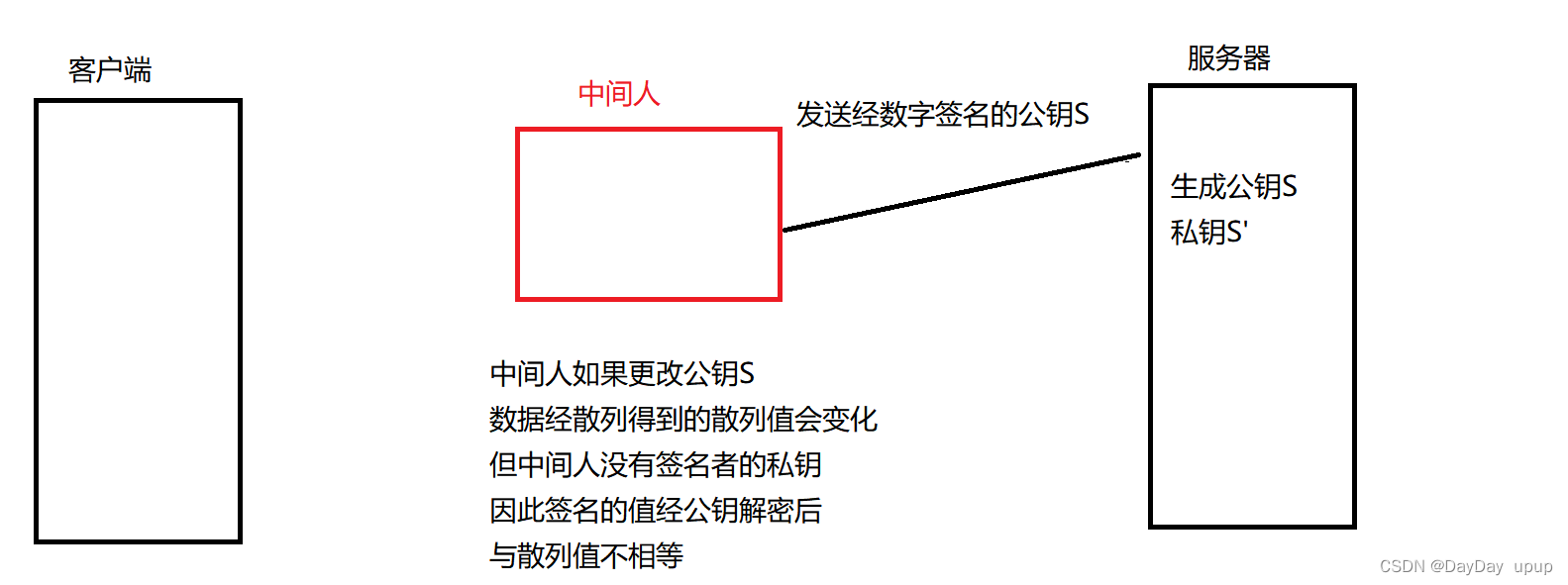
https协议
文章目录对称加密方案非对称加密方案对称加密方案非对称加密方案对称加密方案非对称加密方案数字证书因为HTTP是明文传输,所以会很有可能产生中间人攻击(获取并篡改传输在客户端及服务端的信息并不被人发觉),HTTPS加密应运而生。 …...
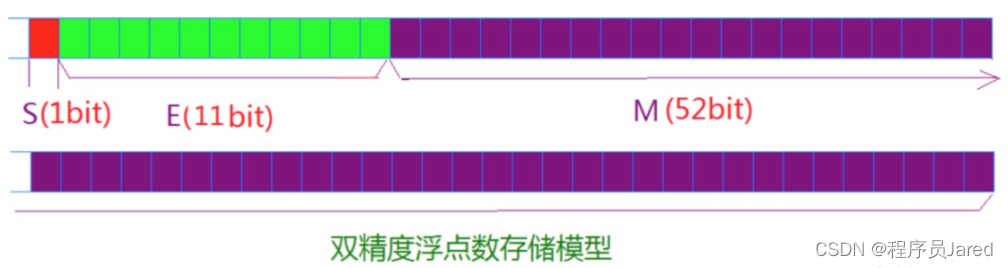
深入浅出C语言——数据在内存中的存储
文章目录一、数据类型详细介绍1. C语言中的内置类型2. 类型的基本归类:二. 整形在内存中的存储1. 原码、反码、补码2. 大小端三.浮点数存储规则一、数据类型详细介绍 1. C语言中的内置类型 C语言的内置类型有char、short、int、long、long long、float、double&…...

在 Centos 上在线安装 GitLab
作为程序员,其中一个愿望是拥有一个自己的代码存储库。在支持私有部署的代码存储库产品中,GitLab 是比较著名的了,所以今天我总结了一下在 Centos 上安装 GitLab 的过程。 依赖 基础依赖 首先,需要安装部分基础的依赖ÿ…...

模型解释性:SHAP包的使用
本篇博客介绍另一种事后可解释性方法:SHAP(SHapley Additive exPlanation)方法。 1. Shapley值理论 Shapley值是博弈论中的一个概念,通过衡量联盟中各成员对联盟总目标的贡献程度,从而根据贡献程度来进行联盟成员的利益分配,避免…...

算法训练营 day45 动态规划 0-1背包理论 分割等和子集
算法训练营 day45 动态规划 0-1背包理论 分割等和子集 0-1背包理论 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 在下面的讲解中&…...

SSM框架
1.mybatis的底层原理 本质上就是使用反射和动态代理来实现对应的映射关系 2.日志级别 3.传递参数 单个参数的传递和多个参数的传递 Emp selectOne(Param(“xingming”) String name); List selectByCondition(Param(“name”) String name,Param(“sal”) double sal); 4.#和…...

教育行业需要什么样的客服系统?
某教育公司拥有素质教育、成人教育、智慧教育等多个业务板块,日常通过电商、线上媒体、线上线下授课等方式进行业务开展和品牌宣传,取得了非常不错的成绩,受到了很多人的好评反馈。 对于这样一个教育公司,客户来源广泛࿰…...

花房集团任命新首席财务官:已跌破IPO发行价,活跃用户下滑
上市刚满2个月,花椒母公司花房集团(HK:03611)的高管就发生了变更。2023年2月12日,花房集团披露的公告显示,董事会宣布赵磊为该公司首席财务官(CFO),自2023年2月10日起生效。 据贝多…...

儿童绘本馆图书借阅租赁知识付费小程序源码交流
1.分类图书 2.书单推荐 4.会员卡次、期限购买 5.借阅时间选择 6.积分签到 7.优惠Q领取 前端uniapp开发 后端thinkphp开发 完全开源 <template> <view class"sp-section sp-index"> <!-- search --> <view class&qu…...

Vue3 中 axios 的安装及使用
目录前言:一、什么是 axios ?二、Axios 的配置项三、Axios 的请求方式四、自定义创建实例五、Axios 请求错误处理六、Axios 解决跨域问题七、Axios 请求案例随机笑话大全总结:前言: 在编写vue里的项目时,必须要用和后台…...

Django设计模式以及模板层介绍
MVC和MTV 传统的MVC作用:降低模块间的耦合度(解耦)Django的MTV模式 作用:降低模块间的耦合度(解耦)什么是模板 1、模板是可以根据字典数据动态变化的html网页2、模板可以根据视图中传递的字典数据动态生成相…...

Linux信号一门搞定
1.信号是什么? 信号其实就是一个软件中断。 例: 输入命令,在Shell下启动一个前台进程。用户按下Ctrl-C,键盘输入产生一个硬件中断。如果CPU当前正在执行这个进程的代码,则该进程的用户空间代码暂停执行,…...

手撸一个动态Feign,实现一个“万能”接口调用
Feign,在微服务框架中,是的服务直接的调用变得很简洁、简单,而不需要再编写Java Http调用其他微服务的接口。 动态feign 对于fegin调用,我们一般的用法:为每个微服务都创建对应的feignclient接口,然后为每…...
Linux Capabilities 入门
目录 Linux capabilities 是什么? capabilities 的赋予和继承 线程的 capabilities Permitted Effective Inheritable Bounding Ambient 文件的 capabilities Permitted Inheritable Effective 运行 execve() 后 capabilities 的变化 案例 Linux capab…...

驱动 day6
关于设备树的理解: 设备树(Device Tree)是一种用于特定硬件设备的解释语法树。它用来表示存储有关主板硬件和CPU架构信息的数据在内核中的传递格式,使内核可以更好地了解硬件并支持它们,而不必编写固定的代码。设备节点…...
附录2-tensorflow目标检测
源码来自作者Bubbliiiing,我对参考链接的代码略有修改,网盘地址 链接:百度网盘 请输入提取码 提取码:dvb1 目录 1 参考链接 2 环境 3 数据集准备 3.1 VOCdevkit/VOC2007 3.2 model_data/voc_classes.txt 3.3 voc_an…...

常见的EMC问题
电磁兼容设计的目的就在于满足产品功能要求、减少调试时间,使产品满足电磁兼容标准的要求,并且使产品不会对系统中的其它设备产生电磁干扰。 电磁兼容设计中常见的问题有哪些? 1、电磁兼容设计可以从电路设计(包括器件选择&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...
