杰林码图像增强算法——超分辨率、图像放大、轮廓和色彩强化算法(二)
一、前言
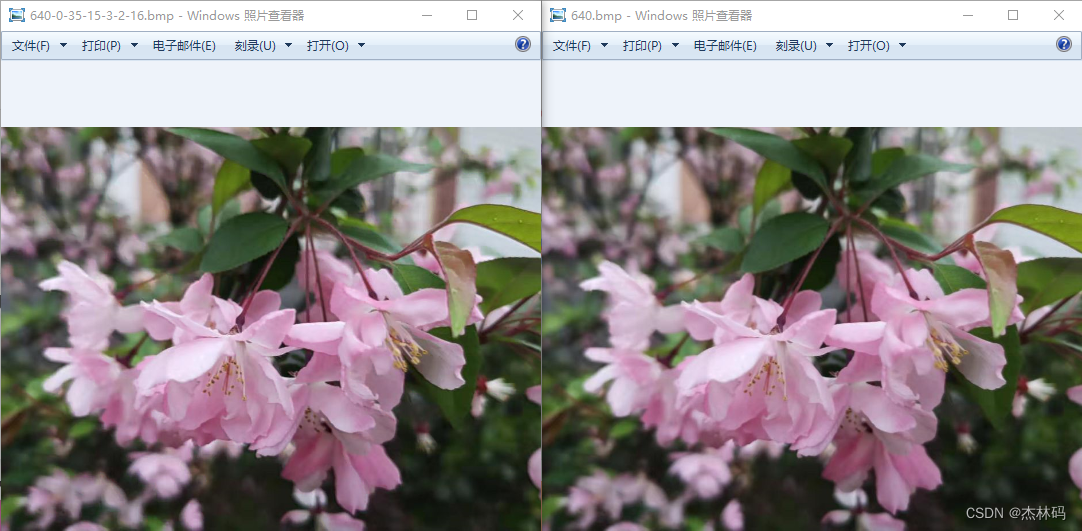
2023-03-23我发布了基于加权概率模型(杰林码的理论模型)的图像颜色增强和轮廓预测的应用方法。效果还不太明显,于是我又花了2周的时间进行了技术优化。下面仅提供了x86下的BMP和JPG对应的lib和dll,本文中的算法属于我国自主的发明专利技术,商用必须获得授权,可提供linux(麒麟、鸿蒙)、x64、riscv、ARM等库,可在GPU上实现视频清晰化处理。在相同的尺寸下加权概率模型优化后的效果:





效率方面还不错,一张1080P的图像大概能在1秒左右运算完毕。如果采用多线程完全可以在GPU上实现多帧优化。上面相关参数设置的比较夸张,实际情况下可以根据个人感觉进行设置。
二、测试程序
int main() { // 3ULONGLONG t1, t2;WJLImageEnhancement wie;int err;char url1[200], url2[200];int i, length;ImageEnhanced imageEnhanced;// 设置对应的参数imageEnhanced.magnification = 0; // 图像放大尺寸,0为不放大仅做清晰化处理imageEnhanced.contour_size = 15; // 轮廓像素范围,影响清晰度和运算效率,越大越清晰但运算所需时间越长imageEnhanced.jielin_ratio = 35; // 杰林码系数0-49共50种值,越接近0则可以分解出背景的子图,越接近50则可以分解出前景子图imageEnhanced.foreground_clear_size = 7; // 前景清晰化的像素范围imageEnhanced.background_clear_size = 3; // 背景清晰化的像素范围imageEnhanced.threshold = 13; // 相邻像素值之差的绝对阈值,当绝对值大于等于threshold时属于需要清晰化的像素值,配合foreground_clear_size和background_clear_size同时使用的const char* fileName = "xxxx"; // xxxx为BMP图像的名称sprintf_s(url1, 200, "D:\\%s.bmp", fileName);sprintf_s(url2, 200, "D:\\%s-%d-%d-%d-%d-%d.bmp", fileName, imageEnhanced.magnification, imageEnhanced.jielin_ratio, imageEnhanced.contour_size, imageEnhanced.foreground_clear_size, imageEnhanced.background_clear_size);// 把灰度图像进行滤波变换t1 = GetTickCount64();err = wie.WJL_BMPFILE_ENHANCEMENT(url1, url2, &imageEnhanced);t2 = GetTickCount64();// 耗时,包括了bmp图像读写和运算部分printf("运算总耗时:%lld ms\n", t2 - t1);system("pause");return 0;
}
三、vs2019下引用的方法
新建一个控制台项目,然后右击:

然后新建一个main.cpp
#include "WJLImageEnhancement.h"
#include <stdio.h>
#include <stdlib.h>
#include <windows.h>
#include <time.h>
#include <math.h>
using namespace std;
#ifdef WIN32
#define inline __inline
#endif // WIN32int main() { // 4ULONGLONG t1, t2;WJLImageEnhancement wie;int err;char url1[200], url2[200];ImageEnhanced imageEnhanced;// 设置对应的参数,根据个人喜好设置imageEnhanced.magnification = 0; // 图像放大尺寸,0为不放大仅做清晰化处理imageEnhanced.contour_size = 15; // 轮廓像素范围,影响清晰度和运算效率,越大越清晰但运算所需时间越长imageEnhanced.jielin_ratio = 35; // 杰林码系数0-49共50种值,越接近0则可以分解出背景的子图,越接近50则可以分解出前景子图imageEnhanced.foreground_clear_size = 5; // 前景清晰化的像素范围imageEnhanced.background_clear_size = 2; // 背景清晰化的像素范围imageEnhanced.threshold = 13; // 相邻像素值之差的绝对阈值,当绝对值大于等于threshold时属于需要清晰化的像素值,配合foreground_clear_size和background_clear_size同时使用的const char* fileName = "heye"; // jpg的文件名sprintf_s(url1, 200, "D:\\%s.jpg", fileName);sprintf_s(url2, 200, "D:\\%s-%d-%d-%d-%d-%d.bmp", fileName, imageEnhanced.magnification, imageEnhanced.jielin_ratio, imageEnhanced.contour_size, imageEnhanced.foreground_clear_size, imageEnhanced.background_clear_size);// 把灰度图像进行滤波变换t1 = GetTickCount64();err = wie.WJL_JPGFILE_ENHANCEMENT(url1, url2, &imageEnhanced);t2 = GetTickCount64();// 耗时printf("变换算法总耗时:%lld ms\n", t2 - t1);system("pause");return 0;
}
比如下面的效果图:
控制台运行时间:
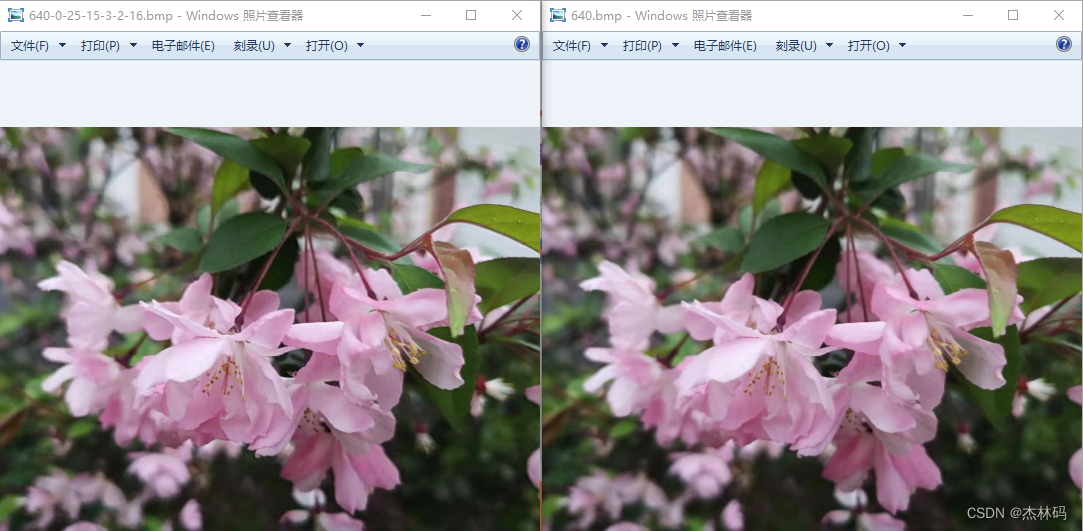
然后比较两张图的效果如下:

参数不同将产生不同的效果:
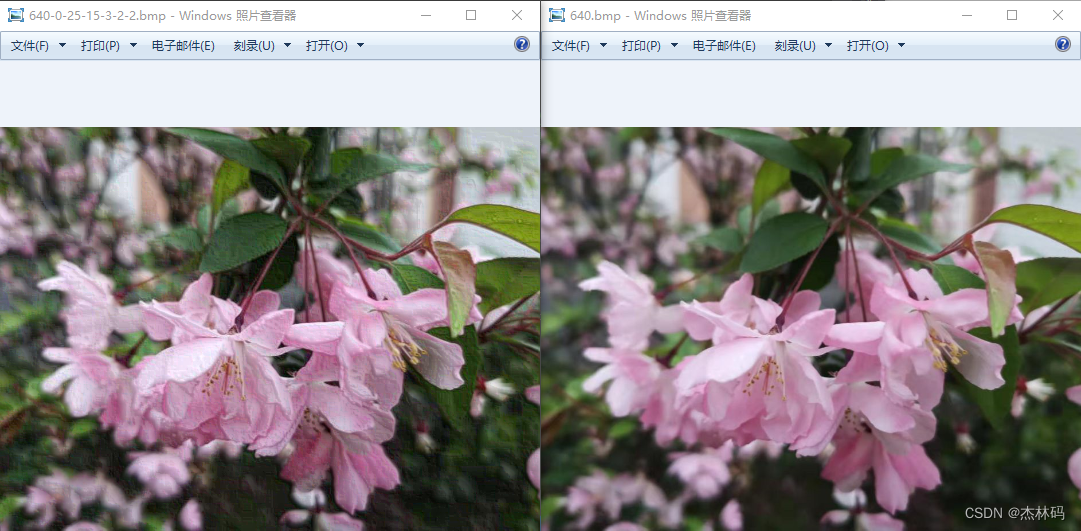
通过测试,各参数的设置取值范围为:
在杰林码超分辨率的算法程序内,主要是ImageEnhanced结构体的参数直接影响到图像输出的质量。
| 参数名称 | 取值范围 | 功能说明 |
|---|---|---|
| magnification | 0-3 | 尺寸放大参数,0表示不放大,1代表图像放大(1+1)(1+1)=4倍,2代表图像放大(2+1)(2+1)=9倍,一般情况下1080P放大到4K输入1即可,一般设置为0-2 |
| jielin_ratio | 0-49 | 杰林码算法的前景背景像素分离的核心参数,越接近0获得的像素块越接近纹理背景,越接近49获得的像素块越接近前景,通过参数设置把图像分割成为前景像素块和背景像素块,属于频率变换算法的一种,一般设置为15-35 |
| contour_size | 4-32 | 这个是以块为单位的轮廓预测参数,一般情况下设置为15,越小效率越高,但是轮廓预测的越不准确,一般设置为15-24 |
| foreground_clear_size | 1-16 | 前景像素块内的连续像素个数,此值越大运算越慢,前景和背景的轮廓越清晰,一般设置为1-8 |
| background_clear_size | 1-8 | 背景纹理预测的连续像素个数,此值越大运算越慢,纹理越清晰,一般设置为1-3 |
相关文章:

杰林码图像增强算法——超分辨率、图像放大、轮廓和色彩强化算法(二)
一、前言 2023-03-23我发布了基于加权概率模型(杰林码的理论模型)的图像颜色增强和轮廓预测的应用方法。效果还不太明显,于是我又花了2周的时间进行了技术优化。下面仅提供了x86下的BMP和JPG对应的lib和dll,本文中的算法属于我国…...

在three.js中废置对象
基于three.js子如何废置对象(How to dispose of objects) 前言: 为了提高性能,并避免应用程序中的内存泄露,一个重要的方面是废置未使用的类库实体。 每当创建一个three.js中的实例时,都会分配一定数量的内存。然而,three.js会创建在渲染中所必需的特定对象, 例如几何…...
Java中的String类真的不可变吗?
其实在Java中,String类被final修饰,主要是为了保证字符串的不可变性,进而保证了它的安全性。那么final到底是怎么保证字符串安全性的呢?接下来就让我们一起来看看吧。 一. final的作用 1. final关键词修饰的类不可以被其他类继…...
电脑重装了系统开不了机怎么办?
我们的电脑办公用久后也会出现故障问题,例如卡顿反应慢等等,这时候就要进行重装系统了,但是很多小伙伴重装系统后会出现开不了机的问题,其实我们比较常见的也就是电脑重装系统开不了机的情况。有很多小伙伴反映自己不知道应该怎么…...
)
SPOJ-NSUBSTR - Substrings(SAM求所有长度子串的最大出现次数)
NSUBSTR - Substrings 题面翻译 你得到了一个最多由 250000250000250000 个小写拉丁字母组成的字符串 SSS。定义 F(x)F(x)F(x) 为 SSS 的某些长度为 xxx 的子串在 SSS 中的最大出现次数。即 F(x)max{times(T)}F(x)max\{times(T)\}F(x)max{times(T)},满足 TTT 是 S…...
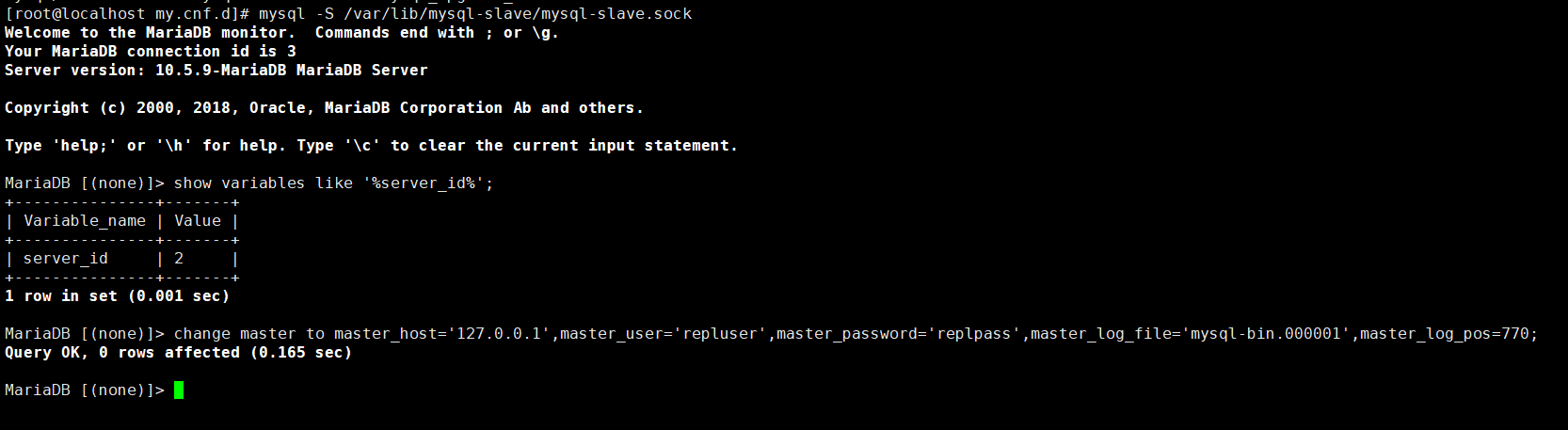
Mariadb10.5基于同服务器多实例主从配置
本次部署环境:Centos8stream 本次部署mariadb版本: mariadb:10.5 本次部署方式:rpm包直接安装,并通过systemd直接托管 可以参考 /usr/lib/systemd/system/mariadb.service 该文件 # Multi instance version of mariadb. For i…...

linux 修改主机名称
1、hostname命令进行临时更改 如果只需要临时更改主机名,可以使用hostname命令: sudo hostname <new-hostname> 例如: 只需重新打开session终端,就能生效, 但是,重启计算机后会回到旧的主机名。…...
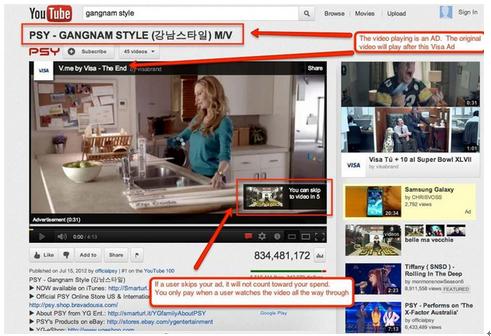
学校的地下网站(学校的地下网站1080P高清)
这个问题本身就提得有问题,为什么这么说,这是因为YouTube本身就不是一个视频网站或者说YouTube不是一个传统的视频网站!!! YouTube能够一家独大,可不仅仅是因为有了Google 这个亲爹,还有一点&am…...

勒索病毒是什么?如何防勒索病毒
勒索病毒并不是某一个病毒,而是一类病毒的统称,主要以邮件、程序、木马、网页挂马的形式进行传播,利用各种加密算法对文件进行加密,被感染者一般无法解密,必须拿到解密的私钥才有可能破解。 已知最早的勒索软件出现于 …...

SpringBoot+VUE+Axios 【链接超时】 后端正常返回结果,前端却出现错误无法接收数据
一、错误原因及解决思路 错误提示表明前端发送的请求在默认的 2500ms 超时时间内没有得到服务器的响应,导致请求失败。尝试以下方法来解决这个问题: 增加请求超时时间:可以通过配置 Axios 请求对象的 timeout 属性来增加请求的超时时间&…...
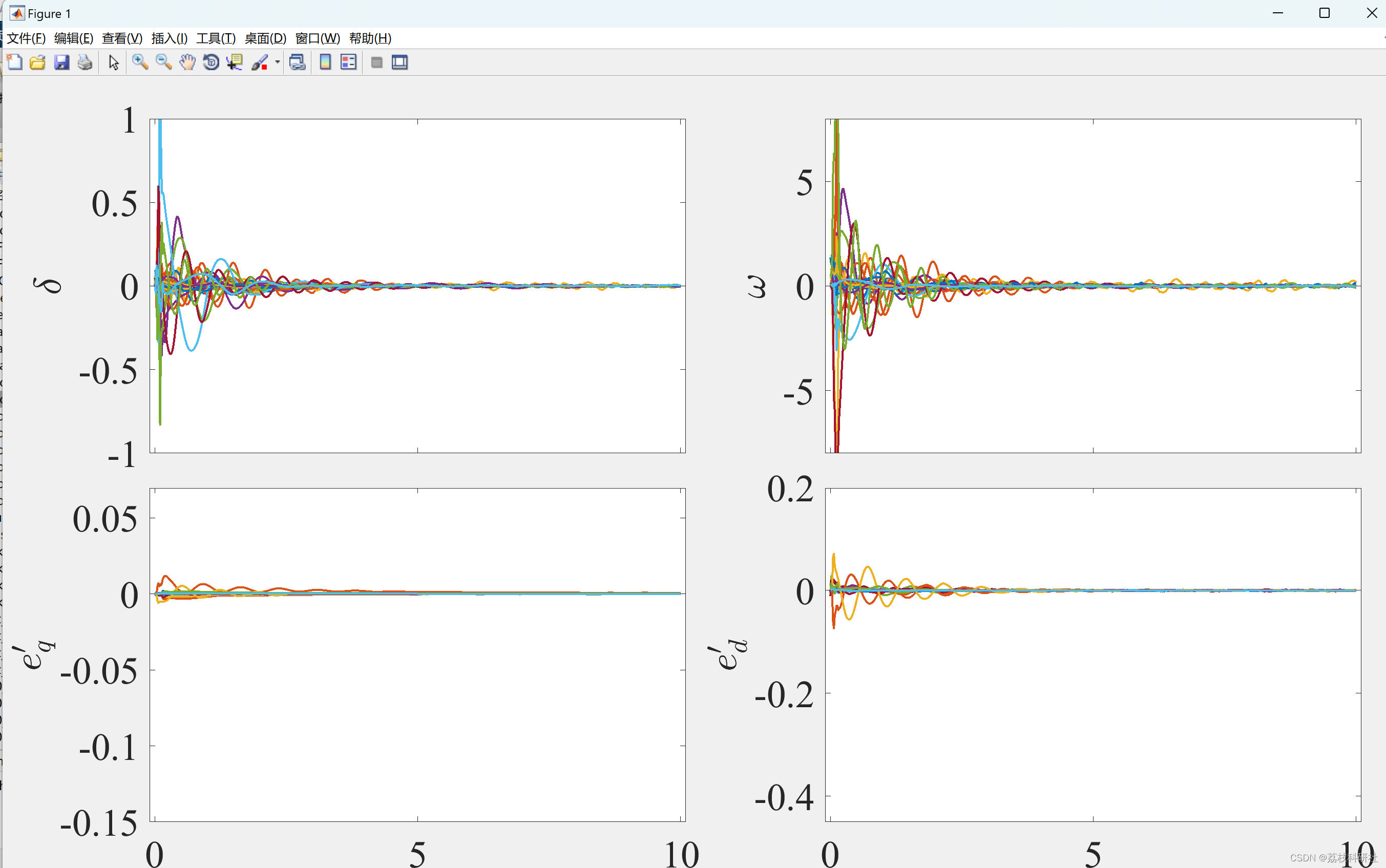
【状态估计】基于增强数值稳定性的无迹卡尔曼滤波多机电力系统动态状态估计(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

快速排序的简单理解
详细描述 快速排序通过一趟排序将待排序列分割成独立的两部分,其中一部分序列的关键字均比另一部分序列的关键字小,则可分别对这两部分序列继续进行排序,以达到整个序列有序的目的。 快速排序详细的执行步骤如下: 从序列中挑出…...
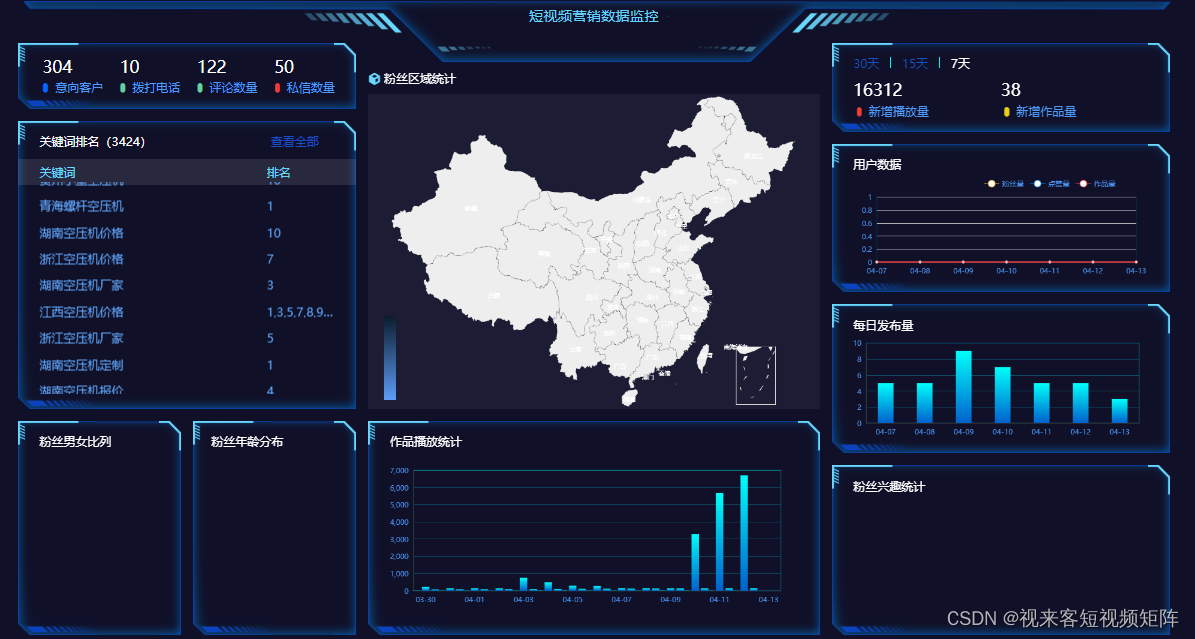
短视频多平台发布软件功能详解
随着移动互联网的普及和短视频的兴起,短视频发布软件越来越受到人们的关注。短视频发布软件除了常规的短视频发布功能,还拥有智能创作、帐号绑定、短视频一键发布、视频任务管理和数据统计等一系列实用功能。下面我们将分步骤详细介绍一下这些功能。 …...

谷歌人机验证Google reCAPTCHA
reCAPTCHA是Google公司推出的一项验证服务,使用十分方便快捷,在国外许多网站上均有使用。它与许多其他的人机验证方式不同,它极少需要用户进行各种识图验证。 它的使用方式如下如所示,只需勾选复选框即可通过人机验证。 虽然简单…...
VB+ACCESS电脑销售系统的设计与实现
为了使此系统简单易学易用、功能强大、软件费用支出低、见效快等特点,我们选择Visual Basic6.0开发此系统。Visual Basic6.0起代码有效率以达到Visual c的水平。在面向对象程序设计方面,Visual Basic6.0全面支持面向对你程序设计包括数据抽象、封装、对象…...

嵌入式开发:硬件和软件越来越接近
从前,硬件和软件工程师大多生活在自己的世界里。硬件团队设计了芯片,调试了从铸造厂返回的第一批样本,让软件团队测试他们的代码。随着虚拟平台和其他可执行模型变得越来越普遍,软件团队可以在芯片制造之前开始,有时甚…...
亲测:腾讯云轻量应用服务器性能如何?
腾讯云轻量应用服务器性能评测,轻量服务器CPU主频、处理器型号、公网带宽、月流量、Ping值测速、磁盘IO读写及使用限制,轻量应用服务器CPU内存性能和标准型云服务器CVM处于同一水准,所以大家不要担心轻量应用服务器的性能,腾讯云百…...
编程语言,TIOBE 4 月榜单:黑马出现了
TIOBE 4 月榜单已经发布了,一起来看看这个月编程语言排行榜有什么变化吧! C 发展依旧迅猛 在本月榜单中,TOP 20 的变动不大,Python、C、Java 、 C 和C#依然占据前五。甚至排名顺序都和上个月一样没有变动。 同时,Rus…...

基于DSP+FPGA的机载雷达伺服控制系统(二)电源仿真
板级电源分配网络的分析与仿真在硬件电路设计中,电源系统的设计是关键步骤之一,良好的电源系统为电路板 上各种信号的传输提供了保障。本章将研究电源完整性的相关问题,并提出一系列改 进电源质量的措施。 3.1 电源完整性 电源完整性…...

SpringBoot整合Redis、以及缓存穿透、缓存雪崩、缓存击穿的理解分布式情况下如何添加分布式锁 【续篇】
文章目录前言1、分布式情况下如何加锁2、具体实现过程3、测试3.1 一个服务按照多个端口同时启动3.2 使用jmeter进行压测前言 上一篇实现了单体应用下如何上锁,这一篇主要说明如何在分布式场景下上锁 上一篇地址:加锁 1、分布式情况下如何加锁 需要注意的点是: 在上锁和释放…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
