【算法题解】24. 模拟机器人行走
这是一道 中等难度 的题
https://leetcode.cn/problems/walking-robot-simulation/description/
题目
机器人在一个无限大小的 XY 网格平面上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令 commands :
- -2 :向左转 90 度
- -1 :向右转 90 度
- 1 <= x <= 9 :向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 obstacles[i] = (xi, yi) 。
机器人无法走到障碍物上,它将会停留在障碍物的前一个网格方块上,但仍然可以继续尝试进行该路线的其余部分。
返回从原点到机器人所有经过的路径点(坐标为整数)的最大欧式距离的平方。(即,如果距离为 5 ,则返回 25 )
注意:
- 北表示 +Y 方向。
- 东表示 +X 方向。
- 南表示 -Y 方向。
- 西表示 -X 方向。
示例 1:
输入:commands = [4,-1,3], obstacles = []
输出:25
解释: 机器人开始位于 (0, 0): 1. 向北移动 4 个单位,到达 (0, 4) 2. 右转 3. 向东移动 3 个单位,到达 (3, 4) 距离原点最远的是 (3, 4) ,距离为 32 + 42 = 25
示例 2:
输入:commands = [4,-1,4,-2,4], obstacles = [[2,4]]
输出:65
解释:机器人开始位于 (0, 0):
1. 向北移动 4 个单位,到达 (0, 4)
2. 右转
3. 向东移动 1 个单位,然后被位于 (2, 4) 的障碍物阻挡,机器人停在 (1, 4)
4. 左转
5. 向北走 4 个单位,到达 (1, 8) 距离原点最远的是 (1, 8) ,距离为 12 + 82 = 65
提示:
- 1<=commands.length<=1041 <= commands.length <= 10^41<=commands.length<=104
- commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9].
- 0<=obstacles.length<=1040 <= obstacles.length <= 10^40<=obstacles.length<=104
- −3∗104<=xi,yi<=3∗104-3 * 104 <= xi, yi <= 3 * 10^4−3∗104<=xi,yi<=3∗104
- 答案保证小于 2312^{31}231
题解思路
这道题理解起来其实很简单,就是求机器人走过的点位当中离原点(0,0)(0,0)(0,0)最远的点(x,y)(x,y)(x,y),并计算其欧式距离的平方。
具体实现逻辑为: 循环遍历命令行数组 commands:
- 如果遇到
-2和-1就切换机器人方向。 - 如果遇到
1 <= x(前进步数) <= 9按照当前方向一步一步前进。- 如果将要前进到的位置
(x, y)在给定的障碍物obstacles数组中,就停下不能走了,也就是直接退出然后执行下一个命令command。 - 否则每走一步,就计算一下
ans = Math.max(ans, x2 + y2)。
- 如果将要前进到的位置
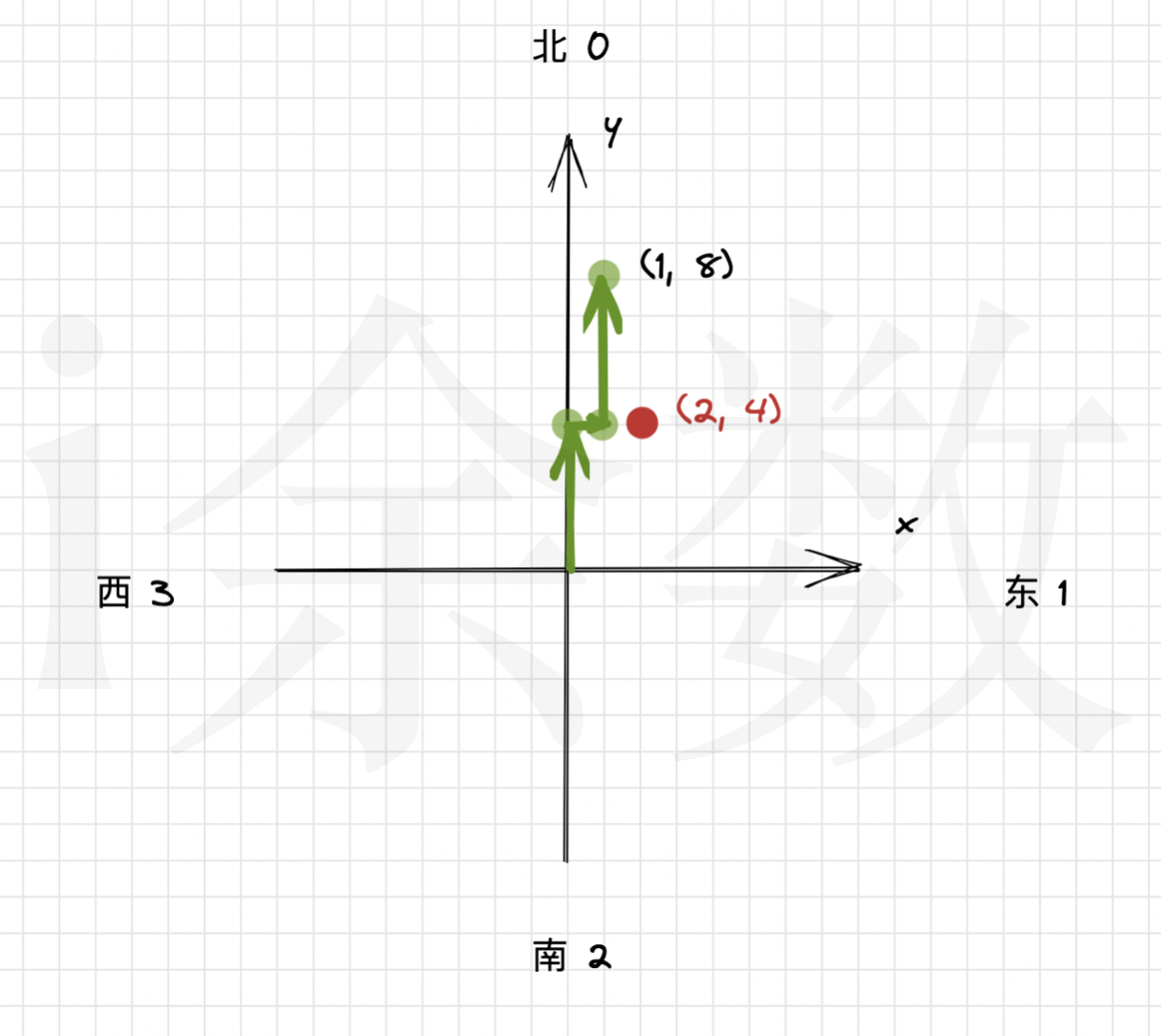
示例2 图示:
代码实现的难点在于方向的切换,这一类题目我们统一采用 方向数组 来处理。
我们定义当前方向为dir,可取值为 {0,1,2,3} ;分别代表 {北,东,南,西} 。见上图。
那么当机器人遇到改变方向的命令时,我们直接修改dir的值即可:
右转:加一,dir = (dir + 1) % 4。
左转:减一,dir = (dir - 1 + 4) % 4。因为dir - 1可能为负,所以先加4。
然后再分别在x 和 y 两个方向上定义两个方向数组,以Java为例:
int[] dx = {0, 1, 0, -1};
int[] dy = {1, 0, -1, 0};
- 方向为北(0)时:每次前进 x 不变,y 加一。
- 方向为东(1)时:每次前进 x 加一,y 不变。
- 方向为南(2)时:每次前进 x 不变,y 减一。
- 方向为西(3)时:每次前进 x 减一,y 不变。
当遇到行走命令时,每前进一步,其位置变换就应该是(x + dx[dir], y + dy[dir])。
另外需要注意的一点是,如果每次判断(x,y)(x, y)(x,y)是不是障碍物点都从 obstaclesobstaclesobstacles 数组找一次的话,那么光查找障碍点的时间复杂度就已经是 O(mn)O(mn)O(mn)了, 其中 mmm 为机器人行走的步数,nnn 为障碍物的个数。我们可以提前以O(n)O(n)O(n)的时间复杂度,将障碍物点初始化到一个哈希表当中,然后我们就可以O(1)O(1)O(1)的时间复杂度来判断一个点是不是障碍物了,具体实现见代码。
代码实现
Java代码实现
class Solution {private Set<Integer> obstacleSet = new HashSet<>();private int factor = 100000;public int robotSim(int[] commands, int[][] obstacles) {genObstacleSet(obstacles);// 当前方向,北:0, 东:1,南:2, 西:3int dir = 0;// 方向数组int[] dx = {0, 1, 0, -1};int[] dy = {1, 0, -1, 0};// 机器人位置int x = 0, y = 0; int ans = 0;for(int command : commands){if(command == -2){dir = (dir + 3) % 4;continue;}if(command == -1){dir = (dir + 1) % 4;continue;}for(int i = 0; i < command; i++){// 如果遇到障碍物,停止在当前位置if(isObstacle(x + dx[dir], y + dy[dir])){break;}x += dx[dir];y += dy[dir];ans = Math.max(ans, x * x + y * y);}}return ans;}// 判断是否是障碍物private boolean isObstacle(int x, int y){return obstacleSet.contains(factor * x + y);}private void genObstacleSet(int[][] obstacles){for(int[] obstacle : obstacles){obstacleSet.add(factor * obstacle[0] + obstacle[1]);}}
}
Go代码实现
func robotSim(commands []int, obstacles [][]int) int {// 初始化障碍点位obstacleMap := make(map[[2]int]bool)for _, obstacle := range obstacles {obstacleMap[[2]int{obstacle[0], obstacle[1]}] = true}// 当前方向dir := 0// 方向数组dx, dy := []int{0, 1, 0, -1}, []int{1, 0, -1, 0}// 当前位置x, y := 0, 0// 答案ans := 0for _, command := range commands {if command == -2 {dir = (dir + 3) % 4continue}if command == -1 {dir = (dir + 1) % 4continue}for i := 0; i < command; i++ {// 遇到障碍物if _, ok := obstacleMap[[2]int{x + dx[dir], y + dy[dir]}]; ok {break;}x += dx[dir]y += dy[dir]ans = max(ans, x * x + y * y)}}return ans}func max(a int, b int) int {if a > b {return a}return b
}
复杂度分析
-
时间复杂度:O(m+n+k)O(m + n + k)O(m+n+k), 其中 mmm 为机器人行走的步数,nnn 为障碍物的个数,kkk为转换方向的次数。
-
空间复杂度:O(n)O(n)O(n), nnn 为障碍物的个数。
相关文章:

【算法题解】24. 模拟机器人行走
这是一道 中等难度 的题 https://leetcode.cn/problems/walking-robot-simulation/description/ 题目 机器人在一个无限大小的 XY 网格平面上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令 commands : -2 &am…...
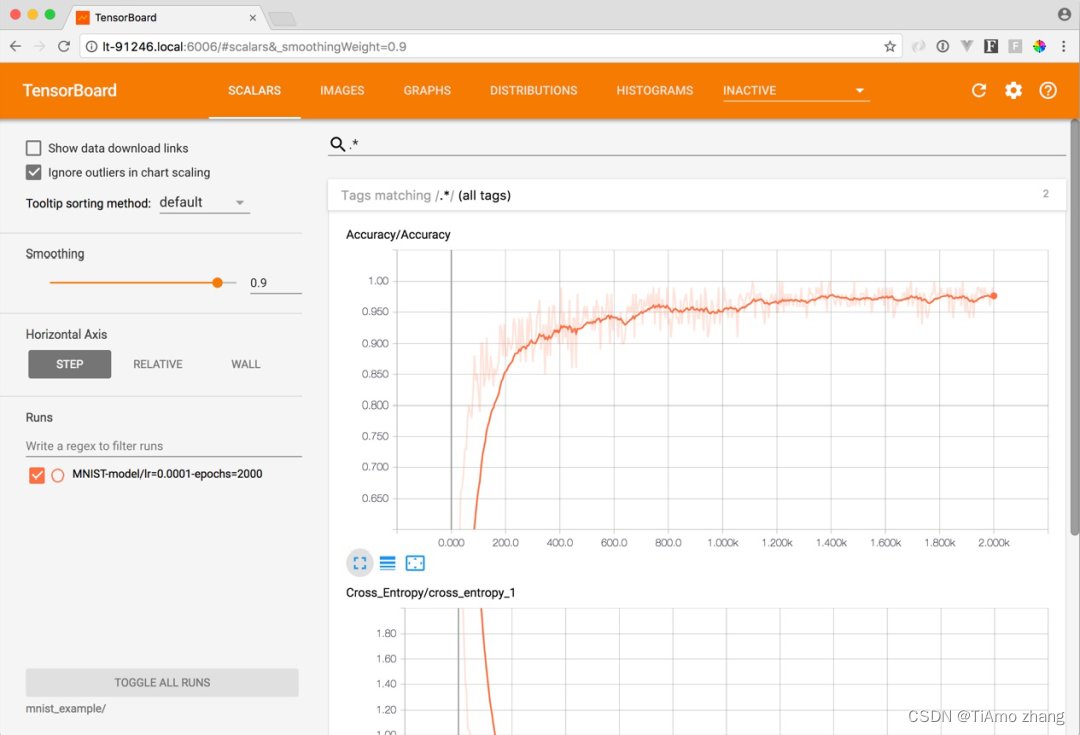
PyTorch 深度学习实战 |用 TensorFlow 训练神经网络
为了更好地理解神经网络如何解决现实世界中的问题,同时也为了熟悉 TensorFlow 的 API,本篇我们将会做一个有关如何训练神经网络的练习,并以此为例,训练一个类似的神经网络。我们即将看到的神经网络,是一个预训练好的用…...

【进阶C语言】静态版通讯录的实现(详细讲解+全部源码)
前言 📕作者简介:热爱跑步的恒川,正在学习C/C、Java、Python等。 📗本文收录于C语言进阶系列,本专栏主要内容为数据的存储、指针的进阶、字符串和内存函数的介绍、自定义类型结构、动态内存管理、文件操作等࿰…...

【JavaWeb】后端(Maven+SpringBoot+HTTP+Tomcat)
目录一、Maven1.什么是Maven?2.Maven的作用?3.介绍4.安装5.IDEA集成Maven6.IDEA创建Maven项目7.IDEA导入Maven项目8.依赖配置9.依赖传递10.依赖范围11.生命周期二、SpringBoot1.Spring2.SpringBoot3.SpringBootWeb快速入门二、HTTP1.HTTP-概述2.HTTP-请求协议3.HTTP-响应协议…...

面试官:准备了一些springboot相关的面试题,快来看看吧
文章目录摘要Spring Boot 中的注解 RestController 和 Controller 有什么区别?Spring Boot 中如何处理异常?使用 ExceptionHandler 注解处理特定类型的异常:使用 ExceptionHandler 注解可以将特定类型的异常映射到一个处理方法上,…...
原子的波尔模型、能量量子化、光电效应、光谱实验、量子态、角动量
一. 卢瑟福模型 1908年,卢瑟福用α粒子继续轰击金箔,发现有极少数粒子,发生了非常大的偏移。而这对于当时主流的葡萄干面包模型理论分析是相悖的。 原子可看成由带正电的原子核和围绕核运动的一些电子组成,原子中心的原子核带正…...

【如何使用Arduino控制WS2812B可单独寻址的LED】
【如何使用Arduino控制WS2812B可单独寻址的LED】 1. 概述2. WS2812B 发光二极管的工作原理3. Arduino 和 WS2812B LED 示例3.1 例 13.2 例 24. 使用 WS2812B LED 的交互式 LED 咖啡桌4.1 原理图4.2 源代码在本教程中,我们将学习如何使用 Arduino 控制可单独寻址的 RGB LED 或 …...
)
计算机基本知识扫盲(持续更)
计算机基本知识扫盲Q:硬盘和磁盘有什么区别?A:硬盘和磁盘都是存储数据的设备。磁盘指的是存储数据的圆形或者是方形的光盘,但是硬盘则是指机械式硬盘和固态硬盘。磁盘一般用于存储少量数据,例如软件安装文件、音乐和电…...

学习大数据需要什么语言基础
Python易学,人人都可以掌握,如果零基础入门数据开发行业的小伙伴,可以从Python语言入手。 Python语言简单易懂,适合零基础入门,在编程语言排名上升最快,能完成数据挖掘、机器学习、实时计算在内的各种大数…...
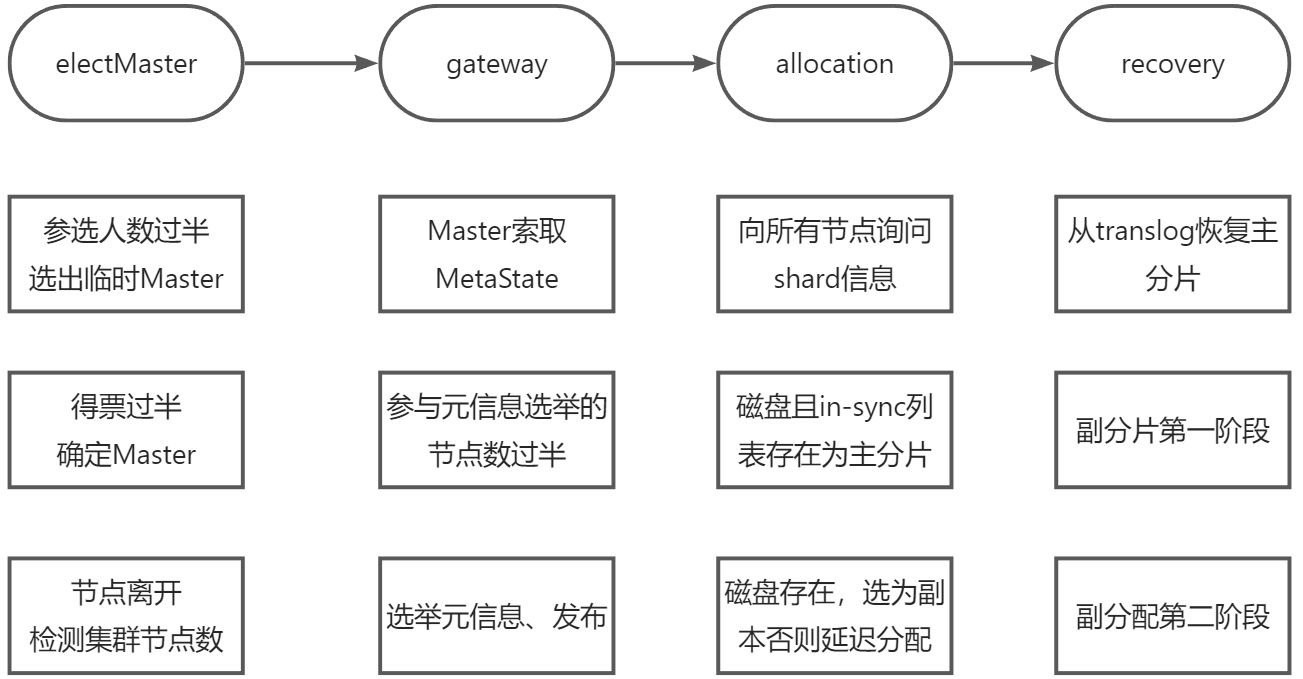
ElasticSearch——详细看看ES集群的启动流程
参考:一起看看ES集群的启动流程 本文主要从流程上介绍整个集群是如何启动的,集群状态如何从Red变成Green,然后分析其他模块的流程。 这里的集群启动过程指集群完全重启时的启动过程,期间要经历选举主节点、主分片、数据恢复等重…...

【教学类-30-01】5以内加法题不重复(一页两份)(包含1以内、2以内、3以内、4以内、5以内加法,抽取最大不重复数量)
作品样式: 背景需求: 虽然学前阶段就对幼儿训练加减法列式题遭到诟病,但是从不少幼儿(特别是二胎)在家中已经开始适应加减法题型了。 结合中班年龄特点,我从5以内的不重复加法题开始实验(雪花…...
写博客8年与人生第一个502万
题记:我们并非生来强大,但依然可以不负青春。 原本想好好写一下如何制定一个目标并通过一点一滴的努力去实现,这三年反思发现其实写自己的经历并不重要。 很多人都听过一句话:榜样的力量是无穷的。 更现实和实际的情况是&#x…...
)
【华为OD机试真题】日志采集系统(javapython)
日志采集系统 时间限制:1s空间限制:256MB限定语言:不限 题目描述: 日志采集是运维系统的的核心组件。日志是按行生成,每行记做一条,由采集系统分 批上报。 如果上报太频繁,会对服务端造成压力;如果上报太晚,会降低用户的体验;如果一 次上报的条数太多,会导致超时…...

epoll源码剖析
文章目录1.前言2.应用层的体现3.两个重要结构(1)eventpoll(2)epitem4.四个函数(1)epoll_create源码(2)epoll_ctl源码(3)epoll_wait的源码(4)epoll_event_callback()5.水平触发和边缘触发1.状态变化2.LT模式3.ET模式1.前言 好久好久没有更新博客了,最近一直在实习&a…...
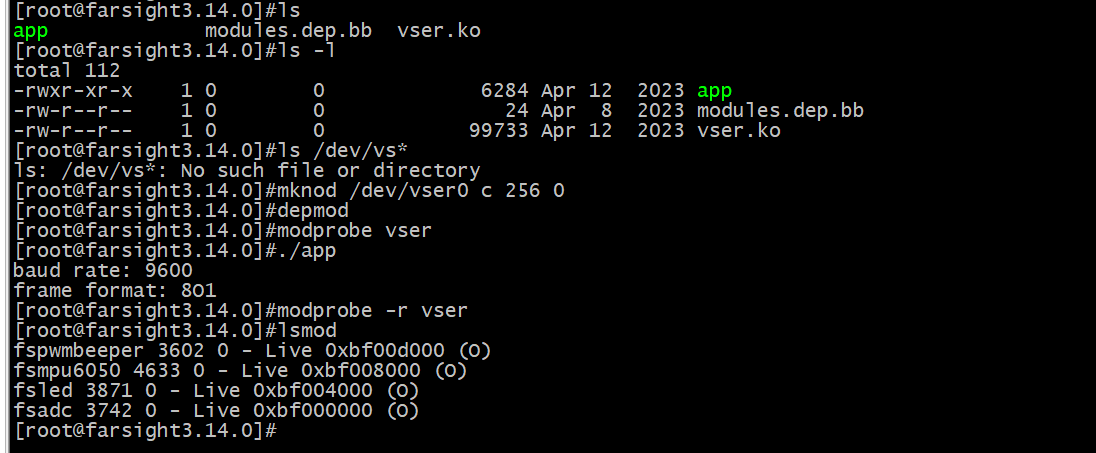
Linux驱动开发——高级I/O操作(一)
一个设备除了能通过读写操作来收发数据或返回、保存数据,还应该有很多其他的操作。比如一个串口设备还应该具备波特率获取和设置、帧格式获取和设置的操作;一个LED设备甚至不应该有读写操作,而应该具备点灯和灭灯的操作。硬件设备是如此众多,…...

适配器模式:C++设计模式中的瑞士军刀
适配器模式揭秘:C设计模式中的瑞士军刀引言设计模式的重要性适配器模式简介与应用场景适配器模式在现代软件设计中的地位与价值适配器模式基本概念适配器模式的定义与核心思想类适配器与对象适配器的比较设计原则与适配器模式的关系类适配器实现类适配器模式的UML图…...

【三十天精通Vue 3】 第三天 Vue 3的组件详解
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录引言一、Vue 3 组件的概述1. Vue 3 的组件系统2. Vue 3 组件的特点…...

SqlServer实用系统视图,你了解多少?
SqlServer实用系统视图,你了解多少?前言master..spt_valuessysdatabasessysprocesses一套组合拳sysobjectssys.all_objectssyscolumnssystypessyscommentssysindexes结束语前言 在使用任何数据库软件的时候,该软件都会提供一些可能不是那么公…...

NodeJS Cluster模块基础教程
Cluster简介 默认情况下,Node.js不会利用所有的CPU,即使机器有多个CPU。一旦这个进程崩掉,那么整个 web 服务就崩掉了。 应用部署到多核服务器时,为了充分利用多核 CPU 资源一般启动多个 NodeJS 进程提供服务,这时就…...
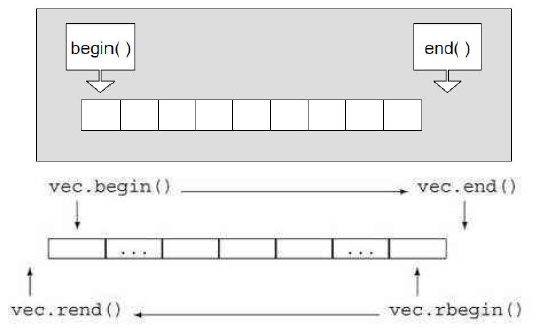
[C++笔记]vector
vector vector的说明文档 vector是表示可变大小数组的序列容器(动态顺序表)。就像数组一样,vector也采用连续的存储空间来储存元素。这就意味着可以用下标对vector的元素进行访问,和数组一样高效。与数组不同的是,它的大小可以动态改变——…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
