密文题解(图论+字典树)
题目大意
有一段长度为nnn的密文,密文的每一位都可以用一个非负整数来描述,并且每一位都有一个权值aia_iai。你可以操作任意多次,每次操作可以选择任意一段密文,花费选择的所有位上权值的异或和的代价获得这段密文每一位的异或和。求至少需要花费多少代价才能将密文的每一位都破解出来。
数据范围
1≤n≤105,0≤ai≤1091\leq n\leq 10^5,0\leq a_i\leq 10^91≤n≤105,0≤ai≤109
题解
令前iii个未知数的异或和为xix_ixi,那么询问[l,r][l,r][l,r]就是询问xr⊕xl−1x_r\oplus x_{l-1}xr⊕xl−1的值。而知道每一个数的值等同于知道每个xix_ixi的值。
一开始,我们只知道x0x_0x0的值。对于一次询问[l,r][l,r][l,r],如果在询问之前我们已经知道xl−1x_{l-1}xl−1的值或xrx_rxr的值,那么询问之后我们就能知道它们两个的值分别为多少。
将每个xix_ixi看作点iii,将询问[l,r][l,r][l,r]看作点l−1l-1l−1向点rrr连一条边,那么题目就转化为求让000到nnn的所有点连通的最小代价,即求最小生成树。
令前iii个aaa值的异或和为sis_isi,那么点iii到点jjj的边的边权为si⊕sjs_i\oplus s_jsi⊕sj。考虑如何求最小生成树。
我们可以把所有sis_isi放在字典树上。对于字典树上的每一个节点,它有两棵子树。只需要从两棵子树中各选一个点,使它们的异或和最小,再把它们连起来,即可将这两部分中的点连通。
那怎么选点呢?我们可以暴力枚举其中一棵子树中的数,然后在另一棵子树上贪心去找与其异或和最小的数,对所有数求最小值即可。
因为每个节点只会被其每个父亲枚举一次,所以这样做的时间复杂度为O(nlog2w)O(n\log^2 w)O(nlog2w),其中www为aia_iai的最大值。
code
#include<bits/stdc++.h>
using namespace std;
const int N=30;
int n,tot=1,tmp,a[100005],s[100005],ch[5000005][2];
vector<int>v[5000005];
long long ans=0;
void pt(int s){int q=1;for(int i=N;i>=0;i--){if(!ch[q][(s>>i)&1]) ch[q][(s>>i)&1]=++tot;q=ch[q][(s>>i)&1];v[q].push_back(s);}
}
int find(int u,int s,int now){int re=0,vq;for(int i=now-1;i>=0;i--){int vq=(s>>i)&1;if(!ch[u][vq]){re|=(1<<i);vq^=1;}u=ch[u][vq];}return re;
}
void gt(int u,int now){--now;if(ch[u][0]) gt(ch[u][0],now);if(ch[u][1]) gt(ch[u][1],now);if(ch[u][0]&&ch[u][1]){tmp=1<<N;for(int i=0;i<v[ch[u][0]].size();i++){tmp=min(tmp,find(ch[u][1],v[ch[u][0]][i],now));}ans+=tmp+(1ll<<now);}
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);s[i]=s[i-1]^a[i];}for(int i=0;i<=n;i++) pt(s[i]);gt(1,N+1);printf("%lld",ans);return 0;
}
相关文章:
)
密文题解(图论+字典树)
题目大意 有一段长度为nnn的密文,密文的每一位都可以用一个非负整数来描述,并且每一位都有一个权值aia_iai。你可以操作任意多次,每次操作可以选择任意一段密文,花费选择的所有位上权值的异或和的代价获得这段密文每一位的异或…...
Baumer工业相机堡盟工业相机如何通过BGAPISDK里的工具函数来计算工业相机的实时帧率(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK里函数来计算相机的实时帧率(C#)Baumer工业相机Baumer工业相机的帧率的技术背景Baumer工业相机的帧率计算方式在BufferEvent声明显示FrameID设计显示帧率的函数Baumer工业相机通过BGAPI SDK计算帧率的优势B…...
)
数据结构与常量(Java)
目录 1.字面常量 2. 数据类型 3. 变量 3.1 变量概念 3.2 语法格式 补充:变量 int long short double和float char boolean byte 4.类型转换 类型提升小结 5. 字符串类型 1. int 转成 String 2. String 转成 int 1.字面常量 类似System.Out.p…...

【LeetCode】剑指 Offer 54. 二叉搜索树的第k大节点 p269 -- Java Version
题目链接:https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/ 1. 题目介绍( 54. 二叉搜索树的第k大节点) 给定一棵二叉搜索树,请找出其中第 k 大的节点的值。 【测试用例】: 示例 1: 示例2&…...
参数)
[工具类] post请求 获取request对象, 获取request的请求体(body)参数
目录 引言: 1. 获取request对象的几种常用方式 -> 1.1 获取请求对象 通过请求上下文对象 获取信息[推荐] -> 1.2 在controller层直接获取[不推荐 侵害性太强] -> 1.3 interceptor中获取[部分业务中使用] -> 1.4 request常用api简介 2. 获取request的body的工具…...

Golang 多版本安装小工具G
voidint制作的Golang版本安装管理,非常好用。想装就装,想换版本就换版本 除了一些使用go install的场景可能有不兼容,主要是安装了工具有时候不能直接用。 GitHub - voidint/g: Golang Version Manager 使用方式很简单&a…...

day29—选择题
文章目录1.HashSet子类依靠什么方法区分重复元素(C)2.以下代码在编译和运行过程中会出现什么情况(A)3.有这么一段程序,执行的结果是(C)1.HashSet子类依靠什么方法区分重复元素(C&…...
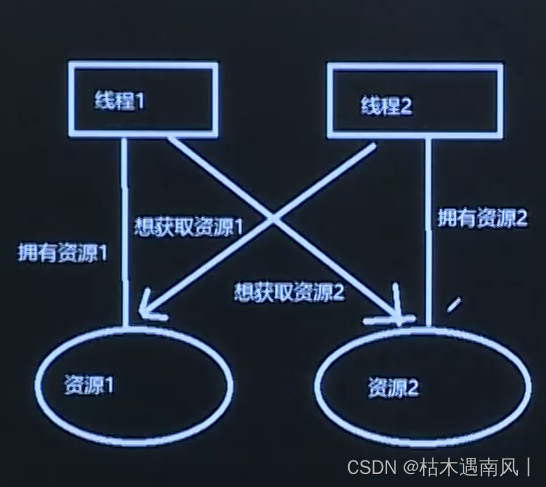
day8 互斥锁/读写锁的概念及使用、死锁的避免
目录 互斥锁的概念和使用 线程通信 - 互斥 互斥锁的创建和销毁 互斥锁的创建 互斥锁的销毁 互斥锁的使用 申请锁 释放锁 互斥锁的概念和使用 线程通信 - 互斥 临界资源: 一次只允许一个任务(进程、线程)访问的共享资源;…...

2023-04-13 monetdb-str类型变长存储-分析
摘要: monetdb的列的基本抽象是BAT,但是对于列数据的存储方式, 对于固定长度和不固定长度,使用了不同的存储方式。 固定长度的数据比如int,int64之类的, 直接存储在了数据tail文件。 但是对于不固定长度比如string, 则使用另外一个独立的theap文件存储, tail文件仅保留对于…...
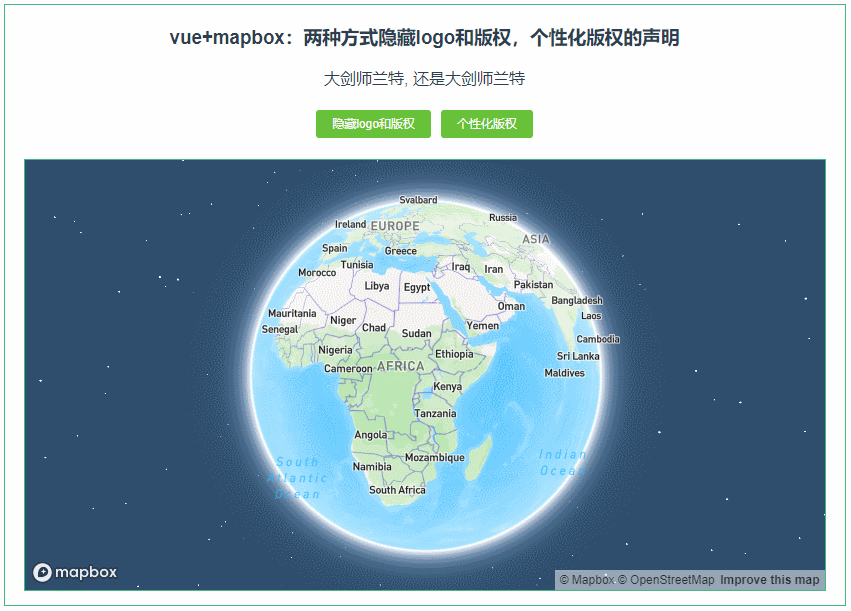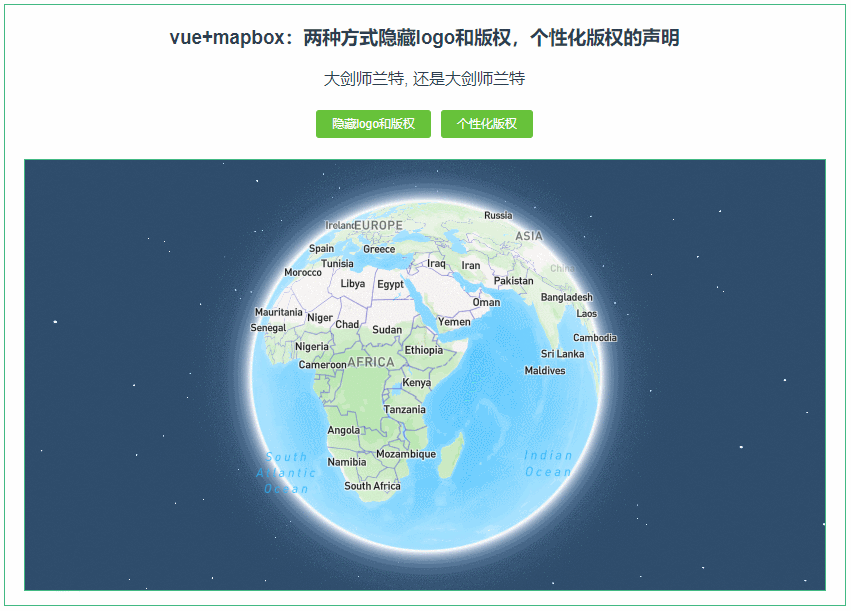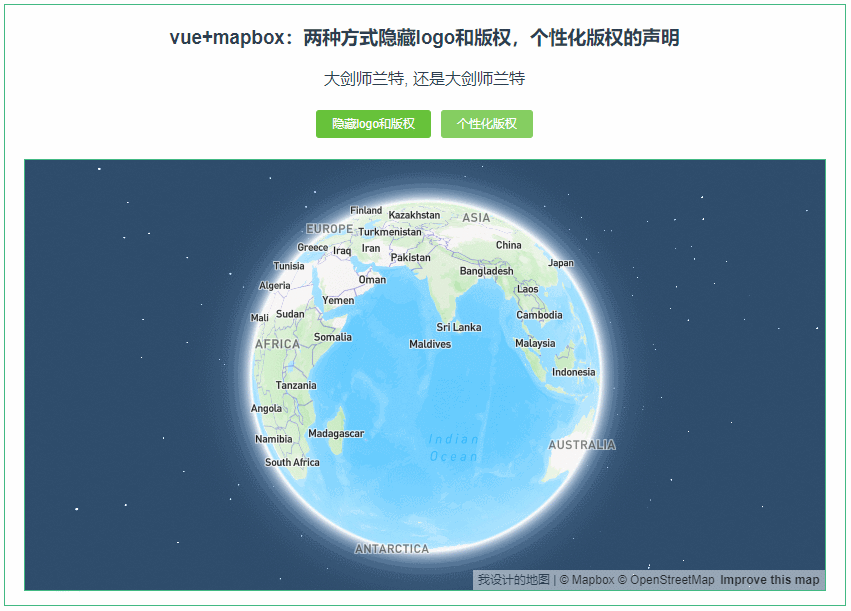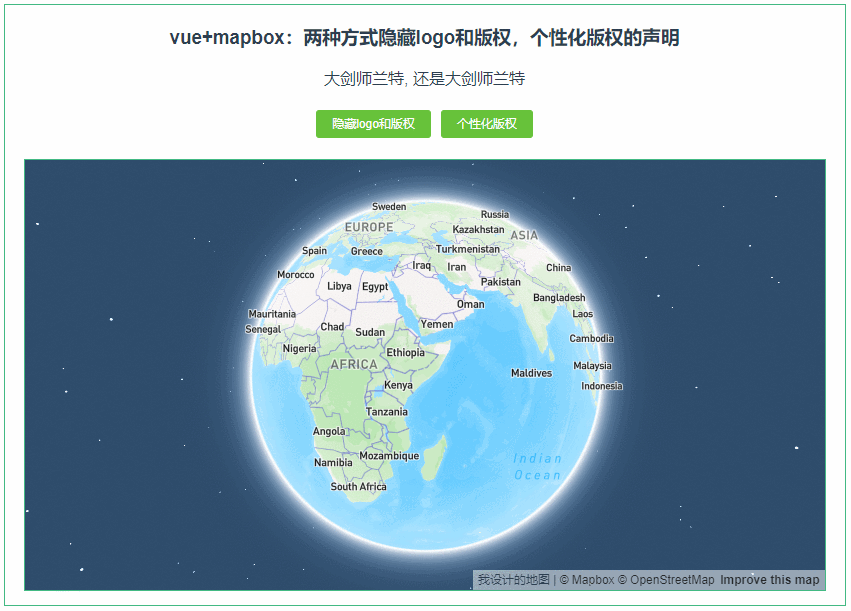
011:Mapbox GL两种方式隐藏logo和版权,个性化版权的声明
第011个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中用两种方式隐藏logo和版权,并个性化版权的声明 。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共91行)相关API参考:专栏目标示例效果 配置方式…...

结合PCA降维的DBSCAN聚类方法(附Python代码)
目录 前言介绍: 1、PCA降维: (1)概念解释: (2)实现步骤: (3)优劣相关: 2、DBSCAN聚类: (1)概念解释&a…...
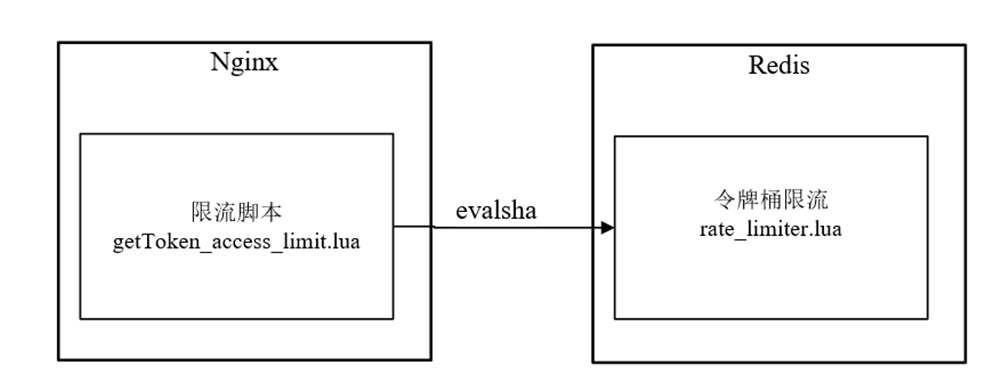
限流:计数器、漏桶、令牌桶 三大算法的原理与实战(史上最全)
限流 限流是面试中的常见的面试题(尤其是大厂面试、高P面试) 注:本文以 PDF 持续更新,最新尼恩 架构笔记、面试题 的PDF文件,请到文末《技术自由圈》公号获取 为什么要限流 简单来说: 限流在很多场景中用来…...
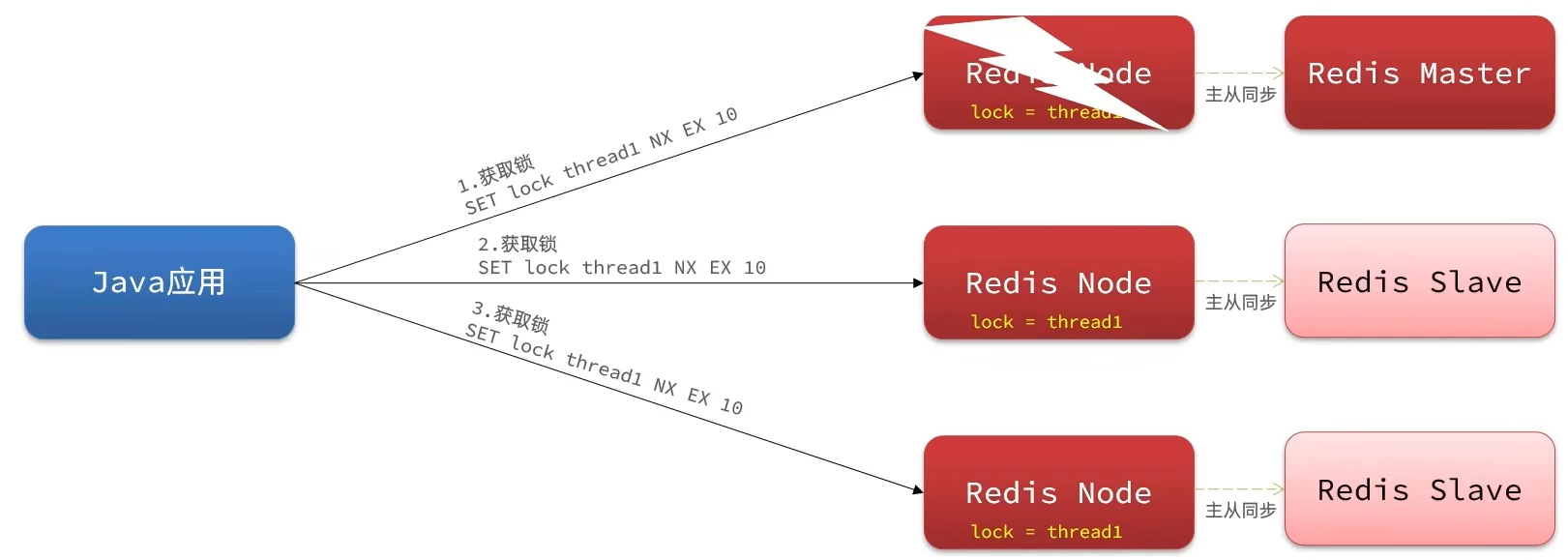
Redis用于全局ID生成器、分布式锁的解决方案
全局ID生成器 每个店铺都可以发布优惠卷 当用户抢购时,就会生成订单并保存到tb_voucher_order这张表中,而订单表如果使用数据库自增id就存在一些问题: 1.id的规律性太明显 2.受单表数据量的限制 全局ID生成器,是一种在分布式系…...
OpenTex 企业内容管理平台
OpenText 企业内容管理平台 将内容服务与领先应用程序集成,弥合内容孤岛、加快信息流并扩大治理 什么是内容服务集成? 内容服务集成通过将内容管理平台与处于流程核心的独立应用程序和系统连接起来,支持并扩展了 ECM 的传统优势。 最好的内…...

【0基础学爬虫】爬虫基础之数据存储
大数据时代,各行各业对数据采集的需求日益增多,网络爬虫的运用也更为广泛,越来越多的人开始学习网络爬虫这项技术,K哥爬虫此前已经推出不少爬虫进阶、逆向相关文章,为实现从易到难全方位覆盖,特设【0基础学…...
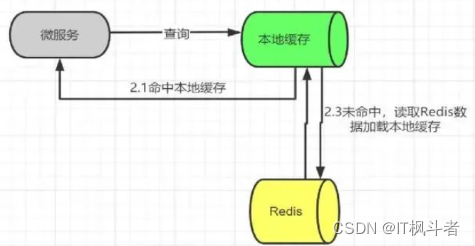
Redis与本地缓存组合使用(IT枫斗者)
Redis与本地缓存组合使用 前言 我们开发中经常用到Redis作为缓存,将高频数据放在Redis中能够提高业务性能,降低MySQL等关系型数据库压力,甚至一些系统使用Redis进行数据持久化,Redis松散的文档结构非常适合业务系统开发…...
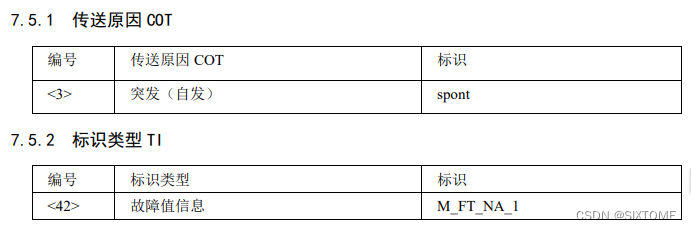
手把手教你学习IEC104协议和编程实现 十 故障事件与复位进程
故障事件 目的 在IEC104普遍应用之前,据我了解多个协议,再综合自动化协议中,有这么一个概念叫“事故追忆”,意思是当变电站出现事故的时候,不但要记录事故的时间,还需记录事故前后模拟量的数据,从而能从一定程度上分析事故产生的原因,这个模拟量就是和今天讲解的故障…...

浅析分布式理论的CAP
大家好,我是易安! 今天让我们来聚焦于分布式系统架构中的重要理论——CAP理论。在分布式系统中,可用性和数据一致性是两个至关重要的因素,而CAP理论就是在这两者之间提供了一种权衡的原则,帮助我们在设计分布式系统时进…...

使用 TensorFlow 构建机器学习项目:6~10
原文:Building Machine Learning Projects with TensorFlow 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...
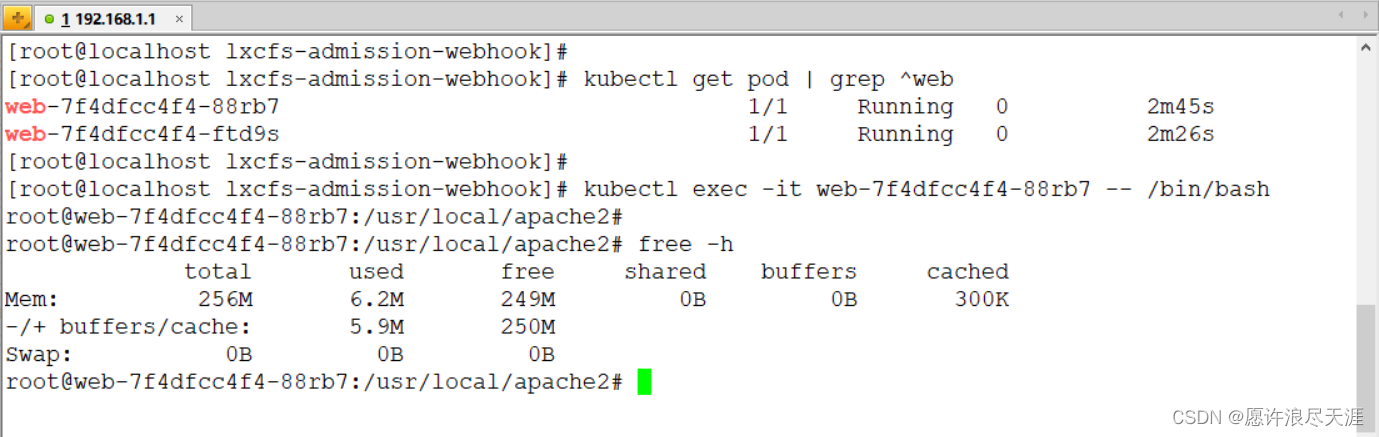
使用 LXCFS 文件系统实现容器资源可见性
使用 LXCFS 文件系统实现容器资源可见性一、基本介绍二、LXCFS 安装与使用1.安装 LXCFS 文件系统2.基于 Docker 实现容器资源可见性3.基于 Kubernetes 实现容器资源可见性前言:Linux 利用 Cgroup 实现了对容器资源的限制,但是当在容器内运行 top 命令时就…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
