结合PCA降维的DBSCAN聚类方法(附Python代码)
目录
前言介绍:
1、PCA降维:
(1)概念解释:
(2)实现步骤:
(3)优劣相关:
2、DBSCAN聚类:
(1)概念解释:
(2)算法原理:
(3)优劣相关:
代码实现:
0、数据准备:
1、PCA降维:
2、DBSCAN聚类:
3、代码汇总:
实现效果:
1、降维效果:
2、聚类效果:
写在最后:
前言介绍:
1、PCA降维:
(1)概念解释:
PCA,全称Principal Component Analysis,即主成分分析。是一种降维方法,实现途径是提取特征的主要成分,从而在保留主要特征的情况下,将高维数据压缩到低维空间。
在经过PCA处理后得到的低维数据,其实是原本的高维特征数据在某一低维平面上的投影(只要维度较低,都可以视为平面,例如三维相对于四维空间也可以视为一个平面)。虽然降维的数据能够反映原本高维数据的大部分信息,但并不能反映原本高维空间的全部信息,因此要根据实际情况,加以鉴别使用。
(2)实现步骤:
PCA主要通过6个步骤加以实现:
1、标准化(将原始数据进行标准化,一般是去均值,如果特征在不同量级上,还要将矩阵除以标准差)
具体:
其中,E为原始矩阵,Emean为均值矩阵,Enorm为标准化矩阵。
2、协方差(计算标准化数据集的协方差矩阵)
具体:
其中,Cov为协方差矩阵,m为样本的数量,Enorm为均值矩阵。
3、特征值(计算协方差矩阵的特征值和特征向量)
具体:
假设实数λ、n行(原始矩阵E的列数即为n)1列的矩阵X(即n维向量)满足下式:
则λ为Cov的特征值,其中Cov为协方差矩阵。
4、K 特征(保留特征值最大的前K个特征(K是降维后,我们期望达到的维度))
具体:
若有多个特征值,则保留前K个最大的特征值,以满足之后的计算需求。
5、K 向量(找到这K个特征值对应的特征向量)
具体:
通过步骤3中的公式得到每个特征值对应的特征向量。
6、得降维(将标准化数据集乘以该K个特征向量,得到降维后的结果)
具体:
其中,Epca为最后要求得的PCA降维矩阵,Enorm为标准化矩阵,X1、X2、X3、...、Xk为对K个特征值对应的特征向量。
(3)优劣相关:
优点:
1.PCA降维之后的各个主成分之间相互正交,可消除原始数据之间相互影响的因素。
2.PCA降维的计算过程并不复杂,因实现起来较简单容易。
3.在保留大部分主要信息的前提下,起到了降维,简便化计算效果。
缺点:
1.特征主成分的定义具有模糊性,解释性差。
2.PCA降维选取令原数据在新坐标轴上方差最大的主成分的标准,使得一些方差小的特征较易丢失,有损失重要信息的可能性。
2、DBSCAN聚类:
(1)概念解释:
密度聚类亦称“基于密度的聚类”(Density-Based Clustering),此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下,密度聚类算法从样本密度的角度来考察样本之间的可连续性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)就是这样一种聚类算法,该算法基于一组“领域”(neighborhood)参数(ε,MinPts)来刻画样本分布的紧密程度。
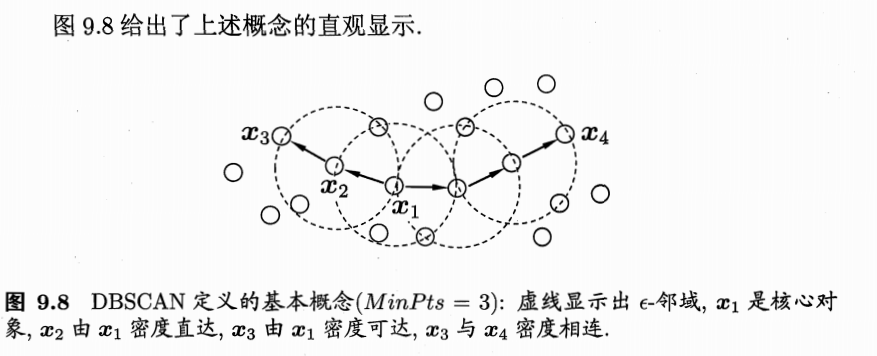
(2)算法原理:
给定数据集D={x1,x2,...,xm},定义下面这几个概念:
理解了相关概念之后,下面给出算法实现的伪代码:
(3)优劣相关:
优点:
1、能够识别任意形状的样本。
2、该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇。
3、无需指定簇个数,而是由算法自主发现。
缺点:
1、需要指定最少点个数(MinPts)与半径(ε)。(但其实相对其他聚类算法来说,已经具有较大的自由性。)
2、最少点个数与半径对算法的影响较大,一般需多次调试。
代码实现:
0、数据准备:
在这里,我们使用sklearn库的鸢尾花iris数据集(sklearn.datasets.load_iris)作为测试数据样本。iris数据集包含150个样本,每个样本包含四个属性特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)和一个类别标签(分别用0、1、2表示山鸢尾、变色鸢尾和维吉尼亚鸢尾)。
首先,我们要安装sklearn库。安装此库,还是通过pip install命令,但是并不是pip install sklearn,而是pip install scikit-learn。正如我们调用opencv是import cv2,而安装却是通过pip install opencv一样。
pip install scikit-learn
然后,获取数据集,其中x为鸢尾花的特征数据集(数据类型为数组numpy.adarray),y为鸢尾花的标签数据集(数据类型为数组numpy.adarray) 。
from sklearn.datasets import load_iris
x = load_iris().data
y = load_iris().target1、PCA降维:
import numpy as npdef PCA_DimRed(dataMat,topNfeat): #PCA_DimRed--PCA dimension reduction,PCA降维meanVals = np.mean(dataMat, axis=0)meanRemoved = dataMat - meanVals # 标准化(去均值)covMat = np.cov(meanRemoved, rowvar=False)eigVals, eigVets = np.linalg.eig(np.mat(covMat)) # 计算矩阵的特征值和特征向量eigValInd = np.argsort(eigVals) # 将特征值从小到大排序,返回的是特征值对应的数组里的下标eigValInd = eigValInd[:-(topNfeat + 1):-1] # 保留最大的前K个特征值redEigVects = eigVets[:, eigValInd] # 对应的特征向量lowDDatMat = meanRemoved * redEigVects # 将数据转换到低维新空间# reconMat = (lowDDatMat * redEigVects.T) + meanVals # 还原原始数据return lowDDatMat2、DBSCAN聚类:
import numpy as np
import random
import copydef DBSCAN_cluster(mat,eps,min_Pts): #进行DBSCAN聚类,优点在于不用指定簇数量,而且适用于多种形状类型的簇k = -1neighbor_list = [] # 用来保存每个数据的邻域omega_list = [] # 核心对象集合gama = set([x for x in range(len(mat))]) # 初始时将所有点标记为未访问cluster = [-1 for _ in range(len(mat))] # 聚类for i in range(len(mat)):neighbor_list.append(find_neighbor(mat, i, eps))if len(neighbor_list[-1]) >= min_Pts:omega_list.append(i) # 将样本加入核心对象集合omega_list = set(omega_list) # 转化为集合便于操作while len(omega_list) > 0:gama_old = copy.deepcopy(gama)j = random.choice(list(omega_list)) # 随机选取一个核心对象k = k + 1Q = list()Q.append(j)gama.remove(j)while len(Q) > 0:q = Q[0]Q.remove(q)if len(neighbor_list[q]) >= min_Pts:delta = neighbor_list[q] & gamadeltalist = list(delta)for i in range(len(delta)):Q.append(deltalist[i])gama = gama - deltaCk = gama_old - gamaCklist = list(Ck)for i in range(len(Ck)):cluster[Cklist[i]] = komega_list = omega_list - Ckreturn cluster3、代码汇总:
from sklearn.datasets import load_iris
import numpy as np
import random
import copy
import matplotlib.pyplot as pltdef PCA_DimRed(dataMat,topNfeat): #PCA_DimRed--PCA dimension reduction,PCA降维meanVals = np.mean(dataMat, axis=0)meanRemoved = dataMat - meanVals # 标准化(去均值)covMat = np.cov(meanRemoved, rowvar=False)eigVals, eigVets = np.linalg.eig(np.mat(covMat)) # 计算矩阵的特征值和特征向量eigValInd = np.argsort(eigVals) # 将特征值从小到大排序,返回的是特征值对应的数组里的下标eigValInd = eigValInd[:-(topNfeat + 1):-1] # 保留最大的前K个特征值redEigVects = eigVets[:, eigValInd] # 对应的特征向量lowDDatMat = meanRemoved * redEigVects # 将数据转换到低维新空间# reconMat = (lowDDatMat * redEigVects.T) + meanVals # 还原原始数据return lowDDatMatdef find_neighbor(data,pos,eps): #寻找相邻点函数N = list()temp = np.sum((data-data[pos])**2, axis=1)**0.5N = np.argwhere(temp <= eps).flatten().tolist()return set(N)def DBSCAN_cluster(data,eps,min_Pts): #进行DBSCAN聚类,优点在于不用指定簇数量,而且适用于多种形状类型的簇,如果使用K均值聚类的话,对于这次实验的数据(条状簇)无法得到较好的分类结果k = -1neighbor_list = [] # 用来保存每个数据的邻域omega_list = [] # 核心对象集合gama = set([x for x in range(len(data))]) # 初始时将所有点标记为未访问cluster = [-1 for _ in range(len(data))] # 聚类for i in range(len(data)):neighbor_list.append(find_neighbor(data, i, eps))if len(neighbor_list[-1]) >= min_Pts:omega_list.append(i) # 将样本加入核心对象集合omega_list = set(omega_list) # 转化为集合便于操作while len(omega_list) > 0:gama_old = copy.deepcopy(gama)j = random.choice(list(omega_list)) # 随机选取一个核心对象k = k + 1Q = list()Q.append(j)gama.remove(j)while len(Q) > 0:q = Q[0]Q.remove(q)if len(neighbor_list[q]) >= min_Pts:delta = neighbor_list[q] & gamadeltalist = list(delta)for i in range(len(delta)):Q.append(deltalist[i])gama = gama - deltaCk = gama_old - gamaCklist = list(Ck)for i in range(len(Ck)):cluster[Cklist[i]] = komega_list = omega_list - Ckreturn clusterif __name__ == "__main__":#1、准备数据x = load_iris().datay = load_iris().target#2、PCA降维pro_data = PCA_DimRed(x,2)#3、DBSCAN聚类(此步中要保证数据集类型为数组,以配合find_neighbor函数)pro_array = np.array(pro_data)thecluster = DBSCAN_cluster(pro_array,eps=0.8,min_Pts=30)#4、展示降维效果:print("下面是降维之前的鸢尾花数据集特征集:")print(x)print("下面是降维之后的鸢尾花数据集特征集:")print(pro_data)#5、展示聚类效果:plt.figure()plt.scatter(pro_array[:, 0], pro_array[:, 1], c=thecluster)plt.show()
实现效果:
1、降维效果:
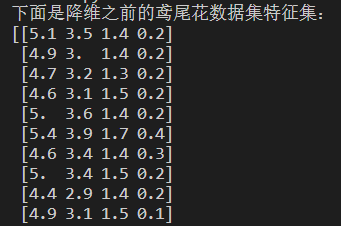
降维之前的鸢尾花数据集特征集:
降维之后的鸢尾花数据集特征集:
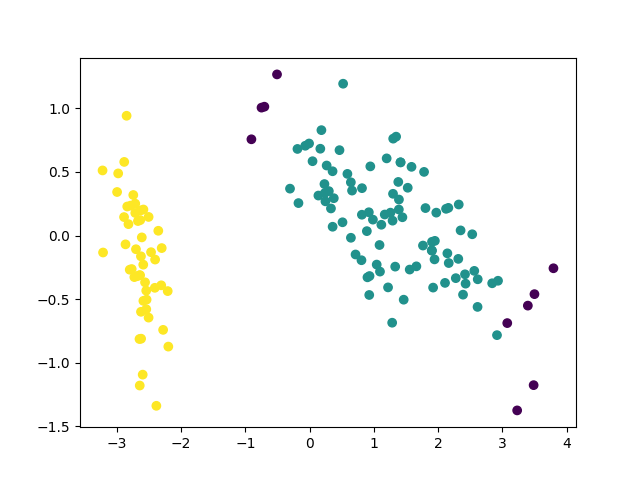
2、聚类效果:
可以看出来,DBSCAN聚类方法并不能很准确地根据PCA降维后的鸢尾花特征集对鸢尾花样本进行聚类,原因是变色鸢尾与维吉尼亚鸢尾的样本特征较近,两者更类似于同属于一个密度空间,因而导致了该实验的不准确性。
但是,其实也可以看出,山鸢尾与其他两种鸢尾能够进行较好的区别 ,说明该方法仍适用于不同类别样本间差距较大的聚类情形。
写在最后:
本篇文章主要介绍了PCA降维、DBSCAN聚类这两个机器学习操作的基本原理,以及两者结合的用于实际数据处理的方法。
可能基于PCA降维的DBSCAN聚类的方法不是很适用于sklearn库中的鸢尾花数据集,但是该方法既具有处理高维数据的能力,也能够处理各种形状的簇,说明其作为一套较为完整的聚类方法,仍然具有较为广阔的应用场景。
希望大家能够积极应用这个方法,使得其拥有更多的应用可能性。谢谢各位!
参考书籍:
周志华.机器学习[M].北京:清华大学出版社,2016.01
参考文章:
六种常见聚类算法:http://t.csdn.cn/Urhn9
Python PCA(主成分分析法)降维的两种实现:http://t.csdn.cn/NlAeU
DBSCAN聚类算法Python实现:http://t.csdn.cn/lkFhF
PCA降维原理 操作步骤与优缺点:http://t.csdn.cn/QiEJM
好了以上就是所有的内容,希望大家多多关注,点赞,收藏,这对我有很大的帮助。谢谢大家了!

好了,这里是Kamen Black 君。祝国康家安,大家下次再见喽!!!
溜溜球~~

相关文章:

结合PCA降维的DBSCAN聚类方法(附Python代码)
目录 前言介绍: 1、PCA降维: (1)概念解释: (2)实现步骤: (3)优劣相关: 2、DBSCAN聚类: (1)概念解释&a…...
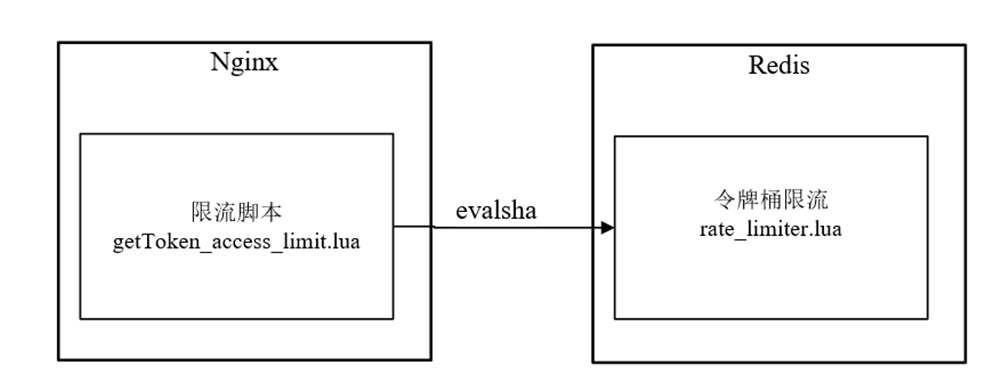
限流:计数器、漏桶、令牌桶 三大算法的原理与实战(史上最全)
限流 限流是面试中的常见的面试题(尤其是大厂面试、高P面试) 注:本文以 PDF 持续更新,最新尼恩 架构笔记、面试题 的PDF文件,请到文末《技术自由圈》公号获取 为什么要限流 简单来说: 限流在很多场景中用来…...
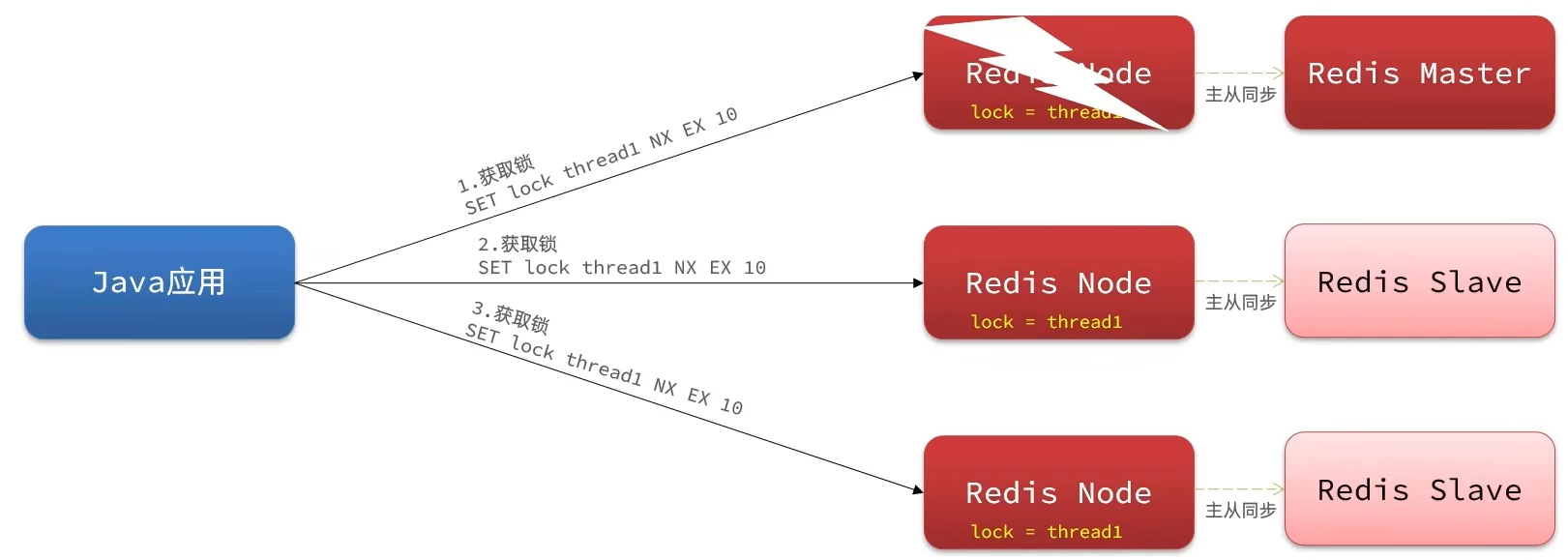
Redis用于全局ID生成器、分布式锁的解决方案
全局ID生成器 每个店铺都可以发布优惠卷 当用户抢购时,就会生成订单并保存到tb_voucher_order这张表中,而订单表如果使用数据库自增id就存在一些问题: 1.id的规律性太明显 2.受单表数据量的限制 全局ID生成器,是一种在分布式系…...
OpenTex 企业内容管理平台
OpenText 企业内容管理平台 将内容服务与领先应用程序集成,弥合内容孤岛、加快信息流并扩大治理 什么是内容服务集成? 内容服务集成通过将内容管理平台与处于流程核心的独立应用程序和系统连接起来,支持并扩展了 ECM 的传统优势。 最好的内…...

【0基础学爬虫】爬虫基础之数据存储
大数据时代,各行各业对数据采集的需求日益增多,网络爬虫的运用也更为广泛,越来越多的人开始学习网络爬虫这项技术,K哥爬虫此前已经推出不少爬虫进阶、逆向相关文章,为实现从易到难全方位覆盖,特设【0基础学…...
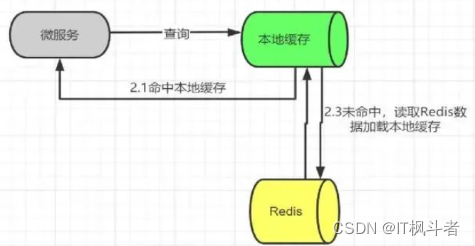
Redis与本地缓存组合使用(IT枫斗者)
Redis与本地缓存组合使用 前言 我们开发中经常用到Redis作为缓存,将高频数据放在Redis中能够提高业务性能,降低MySQL等关系型数据库压力,甚至一些系统使用Redis进行数据持久化,Redis松散的文档结构非常适合业务系统开发…...
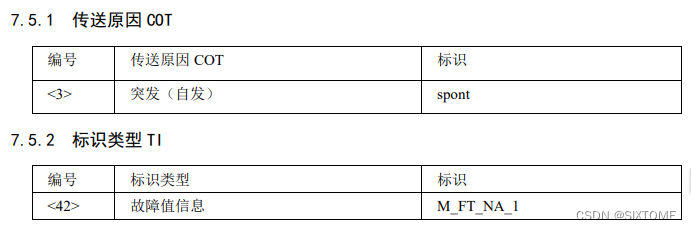
手把手教你学习IEC104协议和编程实现 十 故障事件与复位进程
故障事件 目的 在IEC104普遍应用之前,据我了解多个协议,再综合自动化协议中,有这么一个概念叫“事故追忆”,意思是当变电站出现事故的时候,不但要记录事故的时间,还需记录事故前后模拟量的数据,从而能从一定程度上分析事故产生的原因,这个模拟量就是和今天讲解的故障…...

浅析分布式理论的CAP
大家好,我是易安! 今天让我们来聚焦于分布式系统架构中的重要理论——CAP理论。在分布式系统中,可用性和数据一致性是两个至关重要的因素,而CAP理论就是在这两者之间提供了一种权衡的原则,帮助我们在设计分布式系统时进…...

使用 TensorFlow 构建机器学习项目:6~10
原文:Building Machine Learning Projects with TensorFlow 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...
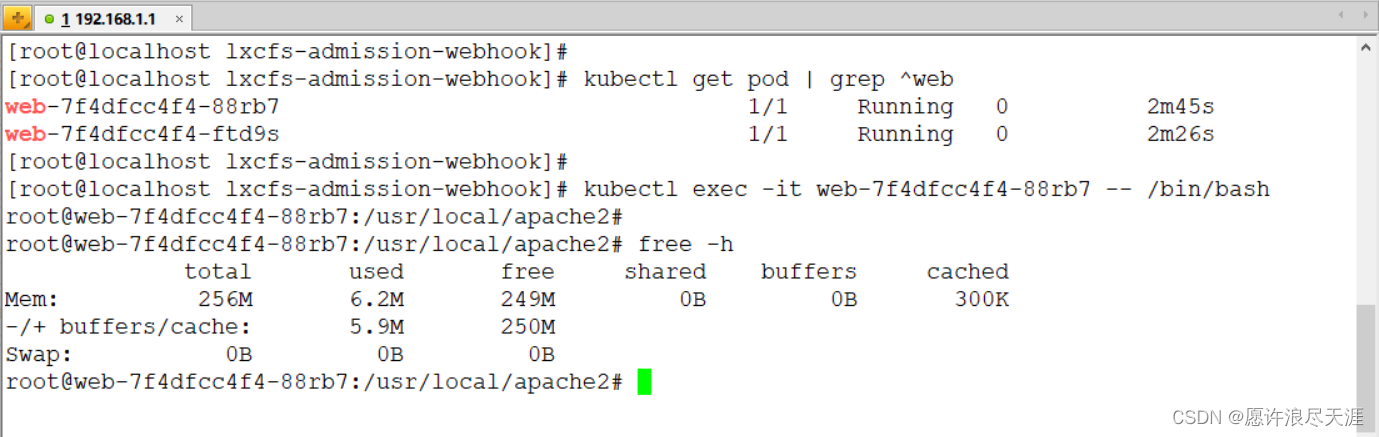
使用 LXCFS 文件系统实现容器资源可见性
使用 LXCFS 文件系统实现容器资源可见性一、基本介绍二、LXCFS 安装与使用1.安装 LXCFS 文件系统2.基于 Docker 实现容器资源可见性3.基于 Kubernetes 实现容器资源可见性前言:Linux 利用 Cgroup 实现了对容器资源的限制,但是当在容器内运行 top 命令时就…...
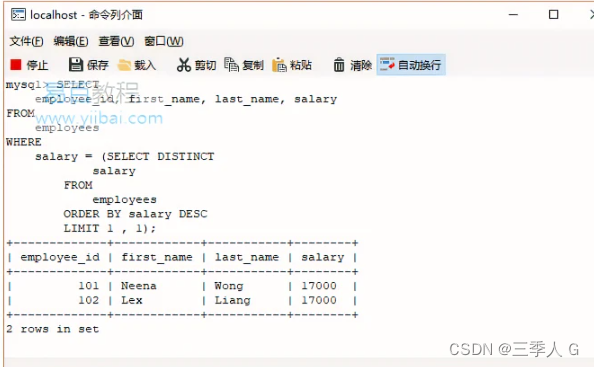
SQL LIMIT
SQL LIMIT SQL LIMIT子句简介 要检索查询返回的行的一部分,请使用LIMIT和OFFSET子句。 以下说明了这些子句的语法: SELECT column_list FROMtable1 ORDER BY column_list LIMIT row_count OFFSET offset;在这个语法中, row_count确定将返…...
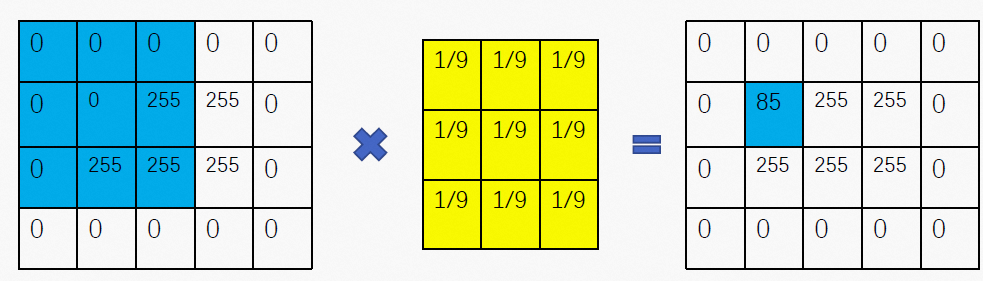
OpenCV实战之人脸美颜美型(六)——磨皮
1.需求分析 有个词叫做“肤若凝脂”,直译为皮肤像凝固的油脂,形容皮肤洁白且光润,这是对美女的一种通用评价。实际生活中我们的皮肤多少会有一些毛孔、斑点等表现,在观感上与上述的“光润感”相反,因此磨皮也成为美颜算法中的一项基础且重要的功能。让皮肤变得更加光润,就…...

Java技术栈—重装系统后不重新安装也能正常使用的设置方式
声明: 最近在重装电脑,重装完后,开发工具会有些功能使用不了,在这做个记录!这里是 JAVA 技术栈 问题描述: git 右键无菜单 111 git git 右键无菜单 参考文章:注册表修复git右键无菜单 git …...
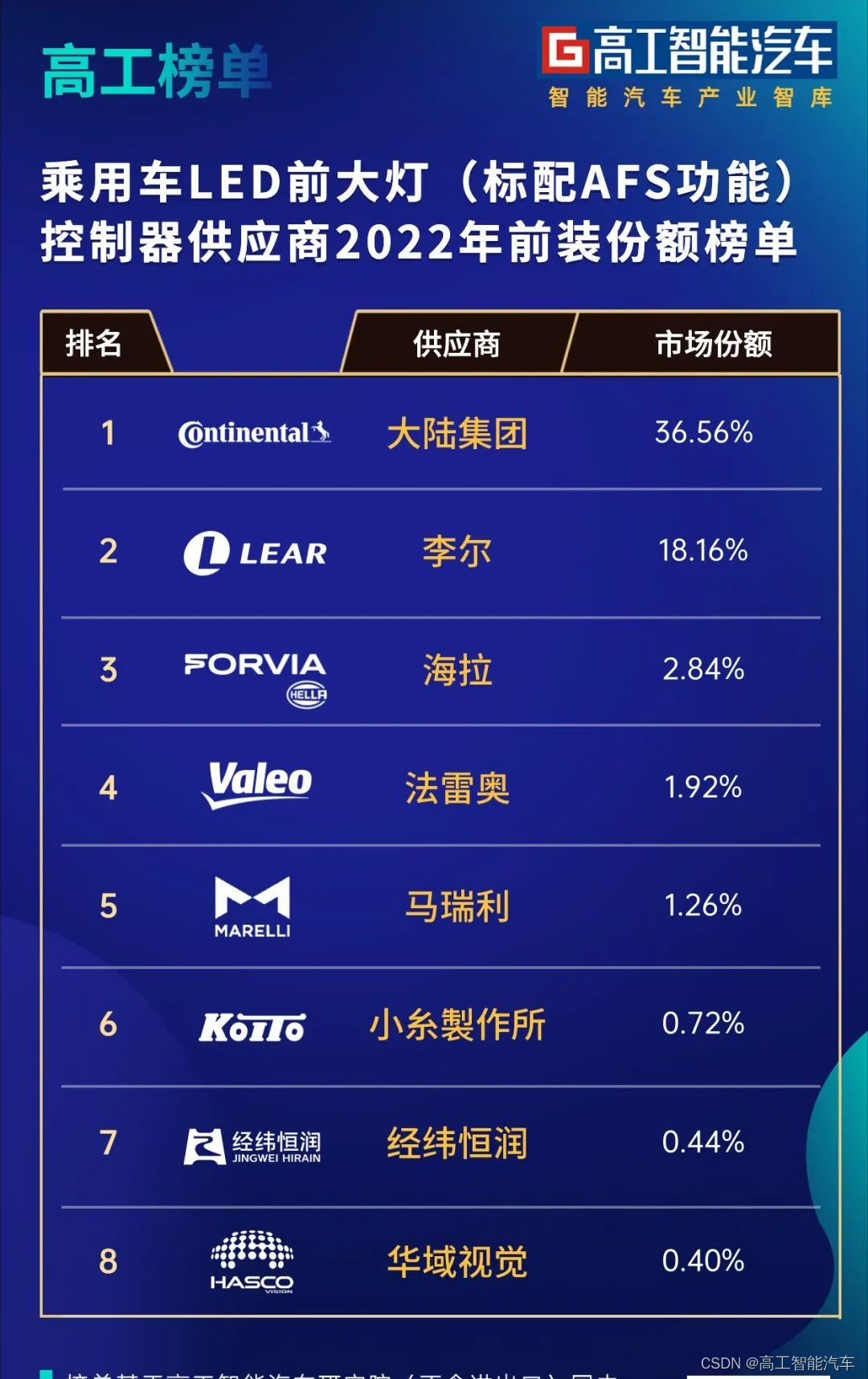
智驾升级!ADB+AFS「起势」
目前,乘用车前大灯已经完成从传统卤素、氙气到LED的转型升级,高工智能汽车研究院监测数据显示,2022年中国市场(不含进出口)乘用车前装标配LED前大灯搭载率达到75.99%,同比2021年提高约7个百分点。 而相比而…...

算法记录 | Day27 回溯算法
39.组合总和 思路: 1.确定回溯函数参数:定义全局遍历存放res集合和单个path,还需要 candidates数组 targetSum(int)目标和。 startIndex(int)为下一层for循环搜索的起始位置。 2.终止条件…...
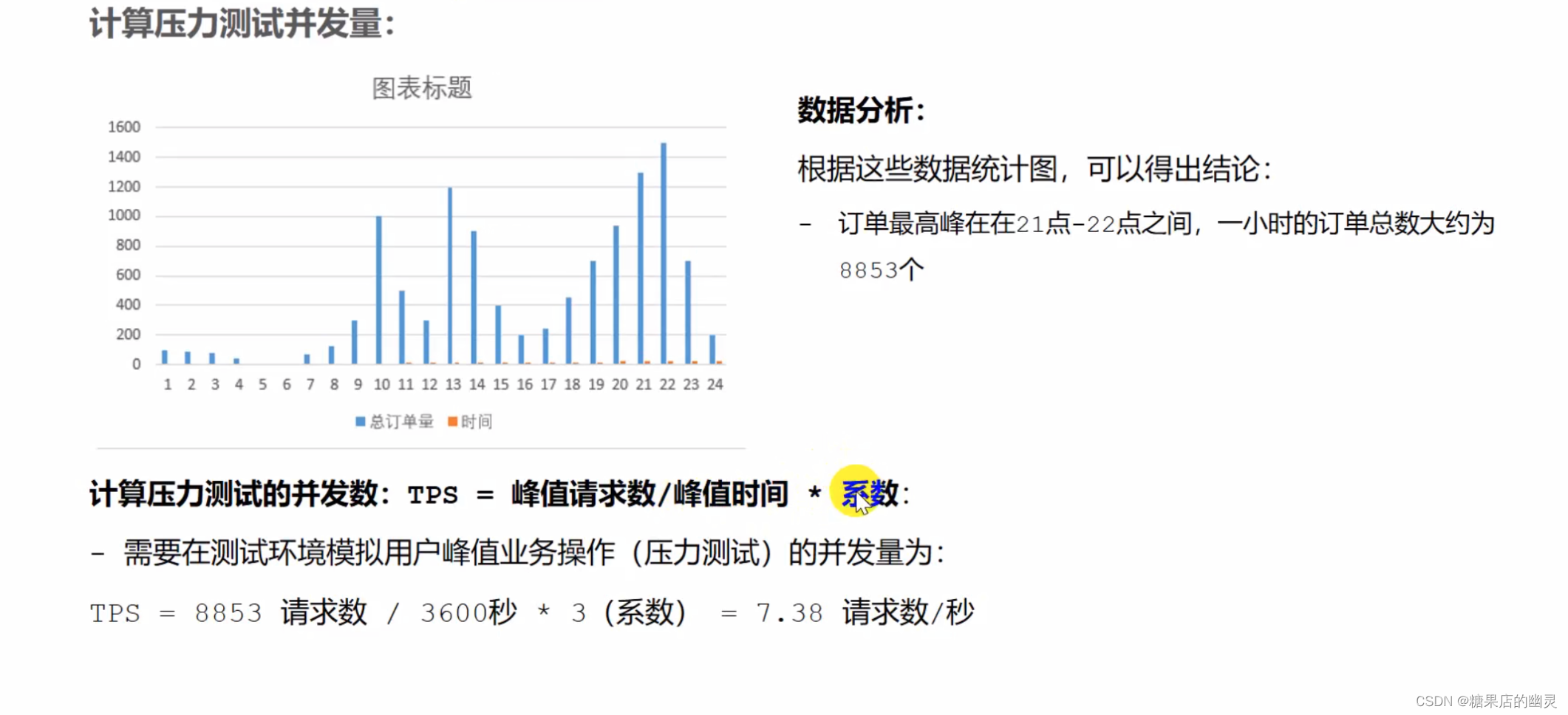
性能测试总结-根据工作经验总结还比较全面
性能测试总结性能测试理论性能测试的策略基准测试负载测试稳定性测试压力测试并发测试性能测试的指标响应时间并发数吞吐量资源指标性能测试流程性能测试工具JMeter基本使用元件构成线程组jmeter的分布式使用jmeter测试报告常用插件性能测试的计算1.根据请求数明细数据计算满足…...

类型断言[as语法 | <> 语法
TypeScript中的类型断言[as语法 | <> 语法] https://huaweicloud.csdn.net/638f0fbbdacf622b8df8e283.html?spm1001.2101.3001.6650.1&utm_mediumdistribute.pc_relevant.none-task-blog-2~default~CTRLIST~activity-1-107633405-blog-122438115.2…...
barret reduction原理详解及硬件优化
背景介绍 约减算法,通常应用在硬件领域,因为模运算mod是一个除法运算,在硬件中实现速度会比乘法慢的多,并且还会占用大量资源,因此需要想办法用乘法及其它简单运算来替代模运算。模约减算法可以利用乘法、加法和移位等…...
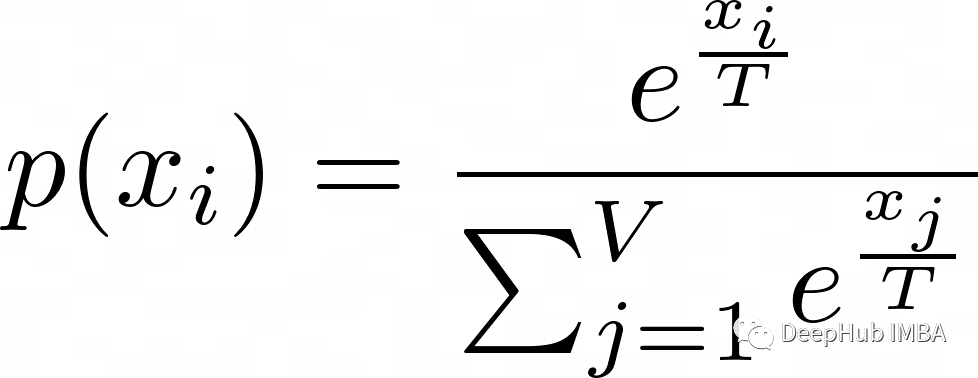
NLP / LLMs中的Temperature 是什么?
ChatGPT, GPT-3, GPT-3.5, GPT-4, LLaMA, Bard等大型语言模型的一个重要的超参数 大型语言模型能够根据给定的上下文或提示生成新文本,由于神经网络等深度学习技术的进步,这些模型越来越受欢迎。可用于控制生成语言模型行为的关键参数之一是Temperature …...

c#快速入门~在java基础上,知道C#和JAVA 的不同即可
☺ 观看下文前提:如果你的主语言是java,现在想再学一门新语言C#,下文是在java基础上,对比和java的不同,快速上手C#,当然不是说学C#的前提是需要java,而是下文是从主语言是java的情况下ÿ…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...