NumPy 秘籍中文第二版:六、特殊数组和通用函数
原文:NumPy Cookbook - Second Edition
协议:CC BY-NC-SA 4.0
译者:飞龙
在本章中,我们将介绍以下秘籍:
- 创建通用函数
- 查找勾股三元组
- 用
chararray执行字符串操作 - 创建一个遮罩数组
- 忽略负值和极值
- 使用
recarray函数创建一个得分表
简介
本章是关于特殊数组和通用函数的。 这些是您每天可能不会遇到的主题,但是它们仍然很重要,因此在此需要提及。**通用函数(Ufuncs)**逐个元素或标量地作用于数组。 Ufuncs 接受一组标量作为输入,并产生一组标量作为输出。 通用函数通常可以映射到它们的数学对等物上,例如加法,减法,除法,乘法等。 这里提到的特殊数组是基本 NumPy 数组对象的所有子类,并提供其他功能。
创建通用函数
我们可以使用frompyfunc() NumPy 函数从 Python 函数创建通用函数。
操作步骤
以下步骤可帮助我们创建通用函数:
-
定义一个简单的 Python 函数以使输入加倍:
def double(a):return 2 * a -
用
frompyfunc()创建通用函数。 指定输入参数的数目和返回的对象数目(均等于1):from __future__ import print_function import numpy as npdef double(a):return 2 * aufunc = np.frompyfunc(double, 1, 1) print("Result", ufunc(np.arange(4)))该代码在执行时输出以下输出:
Result [0 2 4 6]
工作原理
我们定义了一个 Python 函数,该函数会将接收到的数字加倍。 实际上,我们也可以将字符串作为输入,因为这在 Python 中是合法的。 我们使用frompyfunc() NumPy 函数从此 Python 函数创建了一个通用函数。 通用函数是 NumPy 类,具有特殊功能,例如广播和适用于 NumPy 数组的逐元素处理。 实际上,许多 NumPy 函数都是通用函数,但是都是用 C 编写的。
另见
frompyfunc()NumPy 函数的文档
查找勾股三元组
对于本教程,您可能需要阅读有关勾股三元组的维基百科页面。 勾股三元组是一组三个自然数,即a < b < c,为此,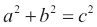 。
。
这是勾股三元组的示例: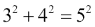 。
。
勾股三元组与勾股定理密切相关,您可能在中学几何学过的。
勾股三元组代表直角三角形的三个边,因此遵循勾股定理。 让我们找到一个分量总数为 1,000 的勾股三元组。 我们将使用欧几里得公式进行此操作:
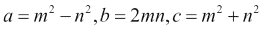
在此示例中,我们将看到通用函数的运行。
操作步骤
欧几里得公式定义了m和n索引。
-
创建包含以下索引的数组:
m = np.arange(33) n = np.arange(33) -
第二步是使用欧几里得公式计算勾股三元组的数量
a,b和c。 使用outer()函数获得笛卡尔积,差和和:a = np.subtract.outer(m ** 2, n ** 2) b = 2 * np.multiply.outer(m, n) c = np.add.outer(m ** 2, n ** 2) -
现在,我们有许多包含
a,b和c值的数组。 但是,我们仍然需要找到符合问题条件的值。 使用where()NumPy 函数查找这些值的索引:idx = np.where((a + b + c) == 1000) -
使用
numpy.testing模块检查解决方案:np.testing.assert_equal(a[idx]**2 + b[idx]**2, c[idx]**2)
以下代码来自本书代码包中的triplets.py文件:
from __future__ import print_function
import numpy as np#A Pythagorean triplet is a set of three natural numbers, a < b < c, for which,
#a ** 2 + b ** 2 = c ** 2
#
#For example, 3 ** 2 + 4 ** 2 = 9 + 16 = 25 = 5 ** 2.
#
#There exists exactly one Pythagorean triplet for which a + b + c = 1000.
#Find the product abc.#1\. Create m and n arrays
m = np.arange(33)
n = np.arange(33)#2\. Calculate a, b and c
a = np.subtract.outer(m ** 2, n ** 2)
b = 2 * np.multiply.outer(m, n)
c = np.add.outer(m ** 2, n ** 2)#3\. Find the index
idx = np.where((a + b + c) == 1000)#4\. Check solution
np.testing.assert_equal(a[idx]**2 + b[idx]**2, c[idx]**2)
print(a[idx], b[idx], c[idx])# [375] [200] [425]
工作原理
通用函数不是实函数,而是表示函数的对象。 工具具有outer()方法,我们已经在实践中看到它。 NumPy 的许多标准通用函数都是用 C 实现的 ,因此比常规的 Python 代码要快。 Ufuncs 支持逐元素处理和类型转换,这意味着更少的循环。
另见
outer()通用函数的文档
使用chararray执行字符串操作
NumPy 具有保存字符串的专用chararray对象。 它是ndarray的子类,并具有特殊的字符串方法。 我们将从 Python 网站下载文本并使用这些方法。 chararray相对于普通字符串数组的优点如下:
- 索引时会自动修剪数组元素的空白
- 字符串末尾的空格也被比较运算符修剪
- 向量化字符串操作可用,因此不需要循环
操作步骤
让我们创建字符数组:
-
创建字符数组作为视图:
carray = np.array(html).view(np.chararray) -
使用
expandtabs()函数将制表符扩展到空格。 此函数接受制表符大小作为参数。 如果未指定,则值为8:carray = carray.expandtabs(1) -
使用
splitlines()函数将行分割成几行:carray = carray.splitlines()以下是此示例的完整代码:
import urllib2 import numpy as np import reresponse = urllib2.urlopen('http://python.org/') html = response.read() html = re.sub(r'<.*?>', '', html) carray = np.array(html).view(np.chararray) carray = carray.expandtabs(1) carray = carray.splitlines() print(carray)
工作原理
我们看到了专门的chararray类在起作用。 它提供了一些向量化的字符串操作以及有关空格的便捷行为。
另见
chararray类的文档
创建遮罩数组
遮罩数组可用于忽略丢失或无效的数据项。 numpy.ma模块中的MaskedArray类是ndarray的子类,带有遮罩。 我们将使用 Lena 图像作为数据源,并假装其中一些数据已损坏。 最后,我们将绘制原始图像,原始图像的对数值,遮罩数组及其对数值。
操作步骤
让我们创建被屏蔽的数组:
-
要创建一个遮罩数组,我们需要指定一个遮罩。 创建一个随机遮罩,其值为
0或1:random_mask = np.random.randint(0, 2, size=lena.shape) -
使用上一步中的遮罩,创建一个遮罩数组:
masked_array = np.ma.array(lena, mask=random_mask)以下是此遮罩数组教程的完整代码:
from __future__ import print_function import numpy as np from scipy.misc import lena import matplotlib.pyplot as pltlena = lena() random_mask = np.random.randint(0, 2, size=lena.shape)plt.subplot(221) plt.title("Original") plt.imshow(lena) plt.axis('off')masked_array = np.ma.array(lena, mask=random_mask) print(masked_array) plt.subplot(222) plt.title("Masked") plt.imshow(masked_array) plt.axis('off') plt.subplot(223) plt.title("Log") plt.imshow(np.log(lena)) plt.axis('off')plt.subplot(224) plt.title("Log Masked") plt.imshow(np.log(masked_array)) plt.axis('off')plt.show()这是显示结果图像的屏幕截图:
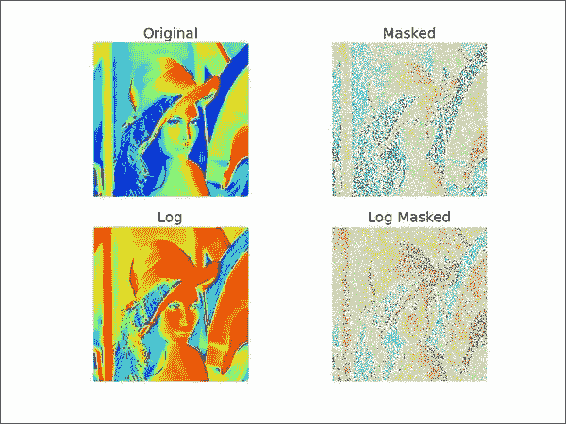
工作原理
我们对 NumPy 数组应用了随机的遮罩。 这具有忽略对应于遮罩的数据的效果。 您可以在numpy.ma 模块中找到一系列遮罩数组操作 。 在本教程中,我们仅演示了如何创建遮罩数组。
另见
numpy.ma模块的文档
忽略负值和极值
当我们想忽略负值时,例如当取数组值的对数时,屏蔽的数组很有用。 遮罩数组的另一个用例是排除极值。 这基于极限值的上限和下限。
我们将把这些技术应用于股票价格数据。 我们将跳过前面几章已经介绍的下载数据的步骤。
操作步骤
我们将使用包含负数的数组的对数:
-
创建一个数组,该数组包含可被三除的数字:
triples = np.arange(0, len(close), 3) print("Triples", triples[:10], "...")接下来,使用与价格数据数组大小相同的数组创建一个数组:
signs = np.ones(len(close)) print("Signs", signs[:10], "...")借助您在第 2 章,“高级索引和数组概念”中学习的索引技巧,将每个第三个数字设置为负数。
signs[triples] = -1 print("Signs", signs[:10], "...")最后,取该数组的对数:
ma_log = np.ma.log(close * signs) print("Masked logs", ma_log[:10], "...")这应该为
AAPL打印以下输出:Triples [ 0 3 6 9 12 15 18 21 24 27] ... Signs [ 1\. 1\. 1\. 1\. 1\. 1\. 1\. 1\. 1\. 1.] ... Signs [-1\. 1\. 1\. -1\. 1\. 1\. -1\. 1\. 1\. -1.] ... Masked logs [-- 5.93655586575 5.95094223368 -- 5.97468290742 5.97510711452 --6.01674381162 5.97889061623 --] ... -
让我们将极值定义为低于平均值的一个标准差,或高于平均值的一个标准差(这仅用于演示目的)。 编写以下代码以屏蔽极值:
dev = close.std() avg = close.mean() inside = numpy.ma.masked_outside(close, avg - dev, avg + dev) print("Inside", inside[:10], "...")此代码显示前十个元素:
Inside [-- -- -- -- -- -- 409.429675172 410.240597855 -- --] ...绘制原始价格数据,绘制对数后的数据,再次绘制指数,最后绘制基于标准差的遮罩后的数据。 以下屏幕截图显示了结果(此运行):
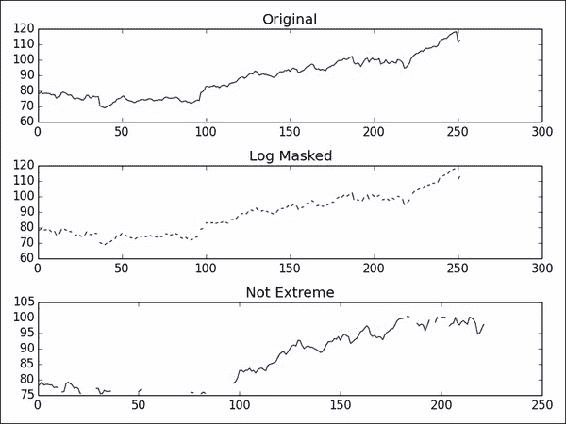
本教程的完整程序如下:
from __future__ import print_function import numpy as np from matplotlib.finance import quotes_historical_yahoo from datetime import date import matplotlib.pyplot as plt def get_close(ticker):today = date.today()start = (today.year - 1, today.month, today.day)quotes = quotes_historical_yahoo(ticker, start, today)return np.array([q[4] for q in quotes])close = get_close('AAPL')triples = np.arange(0, len(close), 3) print("Triples", triples[:10], "...")signs = np.ones(len(close)) print("Signs", signs[:10], "...")signs[triples] = -1 print("Signs", signs[:10], "...")ma_log = np.ma.log(close * signs) print("Masked logs", ma_log[:10], "...")dev = close.std() avg = close.mean() inside = np.ma.masked_outside(close, avg - dev, avg + dev) print("Inside", inside[:10], "...")plt.subplot(311) plt.title("Original") plt.plot(close)plt.subplot(312) plt.title("Log Masked") plt.plot(np.exp(ma_log))plt.subplot(313) plt.title("Not Extreme") plt.plot(inside)plt.tight_layout() plt.show()
工作原理
numpy.ma模块中的函数掩盖了数组元素,我们认为这些元素是非法的。 例如,log()和sqrt()函数不允许使用负值。 屏蔽值类似于数据库和编程中的NULL或None值。 具有屏蔽值的所有操作都将导致屏蔽值。
另见
numpy.ma模块的文档
使用recarray函数创建得分表
recarray类是ndarray的子类。 这些数组可以像数据库中一样保存记录,具有不同的数据类型。 例如,我们可以存储有关员工的记录,其中包含诸如薪水之类的数字数据和诸如员工姓名之类的字符串。
现代经济理论告诉我们,投资归结为优化风险和回报。 风险是由对数回报的标准差表示的。 另一方面,奖励由对数回报的平均值表示。 我们可以拿出相对分数,高分意味着低风险和高回报。 这只是理论上的,未经测试,所以不要太在意。 我们将计算几只股票的得分,并将它们与股票代号一起使用 NumPy recarray()函数中的表格格式存储。
操作步骤
让我们从创建记录数组开始:
-
为每个记录创建一个包含符号,标准差得分,平均得分和总得分的记录数组:
weights = np.recarray((len(tickers),), dtype=[('symbol', np.str_, 16), ('stdscore', float), ('mean', float), ('score', float)]) -
为了简单起见,请根据对数收益在循环中初始化得分:
for i, ticker in enumerate(tickers):close = get_close(ticker)logrets = np.diff(np.log(close))weights[i]['symbol'] = tickerweights[i]['mean'] = logrets.mean()weights[i]['stdscore'] = 1/logrets.std()weights[i]['score'] = 0如您所见,我们可以使用在上一步中定义的字段名称来访问元素。
-
现在,我们有一些数字,但是它们很难相互比较。 归一化分数,以便我们以后可以将它们合并。 在这里,归一化意味着确保分数加起来为:
for key in ['mean', 'stdscore']:wsum = weights[key].sum()weights[key] = weights[key]/wsum -
总体分数将只是中间分数的平均值。 对总分上的记录进行排序以产生排名:
weights['score'] = (weights['stdscore'] + weights['mean'])/2 weights['score'].sort()The following is the complete code for this example:
from __future__ import print_function import numpy as np from matplotlib.finance import quotes_historical_yahoo from datetime import datetickers = ['MRK', 'T', 'VZ']def get_close(ticker):today = date.today()start = (today.year - 1, today.month, today.day)quotes = quotes_historical_yahoo(ticker, start, today)return np.array([q[4] for q in quotes])weights = np.recarray((len(tickers),), dtype=[('symbol', np.str_, 16), ('stdscore', float), ('mean', float), ('score', float)])for i, ticker in enumerate(tickers):close = get_close(ticker)logrets = np.diff(np.log(close))weights[i]['symbol'] = tickerweights[i]['mean'] = logrets.mean()weights[i]['stdscore'] = 1/logrets.std()weights[i]['score'] = 0for key in ['mean', 'stdscore']:wsum = weights[key].sum()weights[key] = weights[key]/wsumweights['score'] = (weights['stdscore'] + weights['mean'])/2 weights['score'].sort()for record in weights:print("%s,mean=%.4f,stdscore=%.4f,score=%.4f" % (record['symbol'], record['mean'], record['stdscore'], record['score']))该程序产生以下输出:
MRK,mean=0.8185,stdscore=0.2938,score=0.2177 T,mean=0.0927,stdscore=0.3427,score=0.2262 VZ,mean=0.0888,stdscore=0.3636,score=0.5561
分数已归一化,因此值介于0和1之间,我们尝试从秘籍开始使用定义获得最佳收益和风险组合 。 根据输出,VZ得分最高,因此是最好的投资。 当然,这只是一个 NumPy 演示,数据很少,所以不要认为这是推荐。
工作原理
我们计算了几只股票的得分,并将它们存储在recarray NumPy 对象中。 这个数组使我们能够混合不同数据类型的数据,在这种情况下,是股票代码和数字得分。 记录数组使我们可以将字段作为数组成员访问,例如arr.field。 本教程介绍了记录数组的创建。 您可以在numpy.recarray模块中找到更多与记录数组相关的功能。
另见
numpy.recarray模块的文档
相关文章:

NumPy 秘籍中文第二版:六、特殊数组和通用函数
原文:NumPy Cookbook - Second Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 在本章中,我们将介绍以下秘籍: 创建通用函数查找勾股三元组用chararray执行字符串操作创建一个遮罩数组忽略负值和极值使用recarray函数创建一…...

各种交叉编译工具链的区别
目录 1 命名规则 2 实例 2.1 arm-none-eabi-gcc 2.2 arm-none-linux-gnueabi-gcc 2.3 arm-eabi-gcc 2.4 armcc 2.5 arm-none-uclinuxeabi-gcc 和 arm-none-symbianelf-gcc 3 gnueabi和gnueabihf的区别(硬浮点、软浮点) 4 Linaro公司出品的交叉编译工具链 5 ARM公司出…...
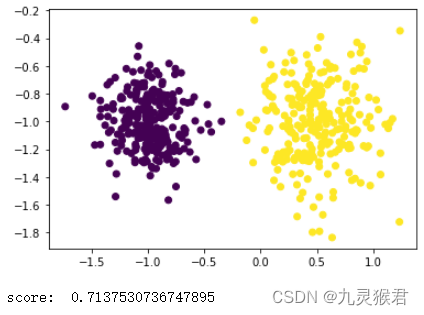
密度聚类算法(DBSCAN)实验案例
密度聚类算法(DBSCAN)实验案例 描述 DBSCAN是一种强大的基于密度的聚类算法,从直观效果上看,DBSCAN算法可以找到样本点的全部密集区域,并把这些密集区域当做一个一个的聚类簇。DBSCAN的一个巨大优势是可以对任意形状…...
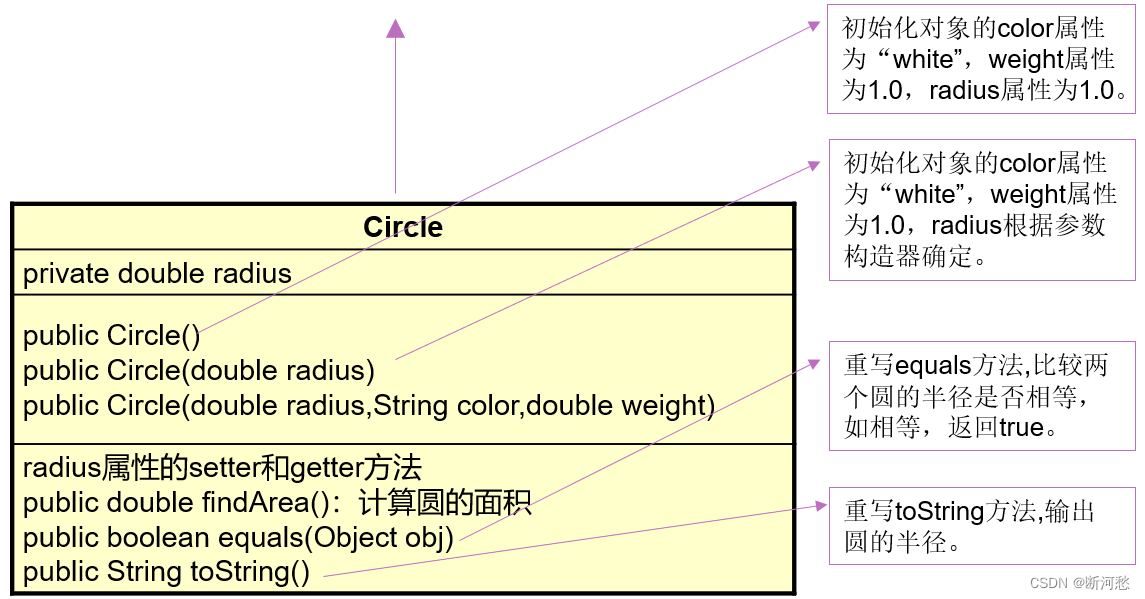
第07章_面向对象编程(进阶)
第07章_面向对象编程(进阶) 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 关键字:this 1.1 this是什么? 在Java中,this关键字不算难理解…...
)
异常的讲解(2)
目录 throws异常处理 基本介绍 throws异常处理注意事项和使用细节 自定义异常 基本概念 自定义异常的步骤 throw 和throws的区别 本章作业 第一题 第二题 第三题 第四题 throws异常处理 基本介绍 1)如果一个方法(中的语句执行时)可能生成某种异常,但是…...

jvm内存结构
1. 栈 程序计数器 2. 虚拟机栈 3. 本地方法栈 4. 堆 5. 方法区 1.2栈内存溢出 栈帧过多导致栈内存溢出 /*** 演示栈内存溢出 java.lang.StackOverflowError* -Xss256k*/ public class Demo1_2 {private static int count;public static void main(String[] args) {try {meth…...

要刹车?生成式AI迎新规、行业连发ChatGPT“警报”、多国考虑严监管
4月13日消息,据中国移动通信联合会元宇宙产业工作委员会网站,中国移动通信联合会元宇宙产业工作委员会、中国通信工业协会区块链专业委员会等,共同发布“关于元宇宙生成式人工智能(类 ChatGPT)应用的行业提示”。提示内…...

轻松掌握Qt FTP 机制:实现高效文件传输
轻松掌握Qt FTP:实现高效文件传输一、简介(Introduction)1.1 文件传输协议(FTP)Qt及其网络模块(Qt and its Network Module)QNetwork:二、QNetworkAccessManager上传实例(Qt FTP Upl…...

用AI帮我写一篇关于FPGA的文章,并推荐最热门的FPGA开源项目
FPGA定义 FPGA(Field Programmable Gate Array)是一种可编程逻辑器件,可以在硬件电路中实现各种不同的逻辑功能。与ASIC(Application Specific Integrated Circuit,特定应用集成电路)相比,FPGA…...

从兴趣或问题出发
当我们还沉寂在移动互联网给生活带来众多便利中,以 ChartGPT 为代表的 AI 时代已彻底到来。科技的发展,时刻在改变着我们的生活,我们需要不断地学习新知识和掌握新技能才能享受变化带来的便利,以及自身不被社会淘汰。 因此&#…...

C++ | 探究拷贝对象时的一些编译器优化
👑作者主页:烽起黎明 🏠学习社区:烈火神盾 🔗专栏链接:C 文章目录前言一、传值传参二、传引用传参三、传值返回拷贝构造和赋值重载的辨析四、传引用返回【❌】五、传匿名对象返回六、总计与提炼前言 在传参…...
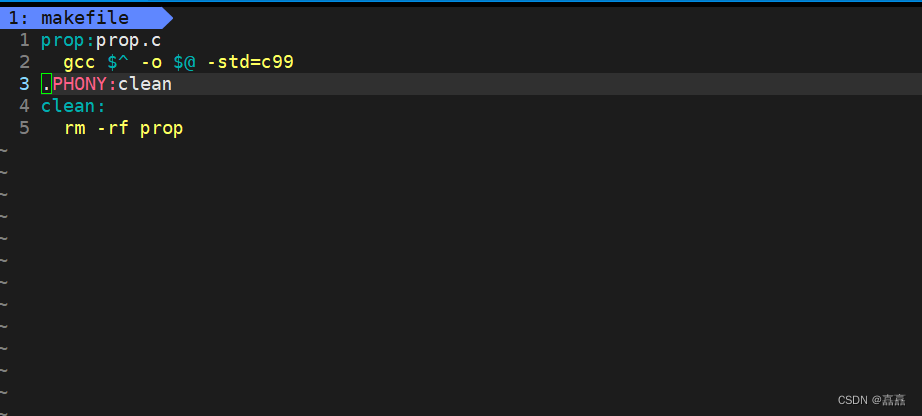
linux工具gcc/g++/gdb/git的使用
目录 gcc/g 基本概念 指令集 函数库 (重要) gdb使用 基本概念 指令集 项目自动化构建工具make/makefile 进度条小程序 编辑 git三板斧 创建仓库 git add git commit git push git status git log gcc/g 基本概念 gcc/g称为编译器…...
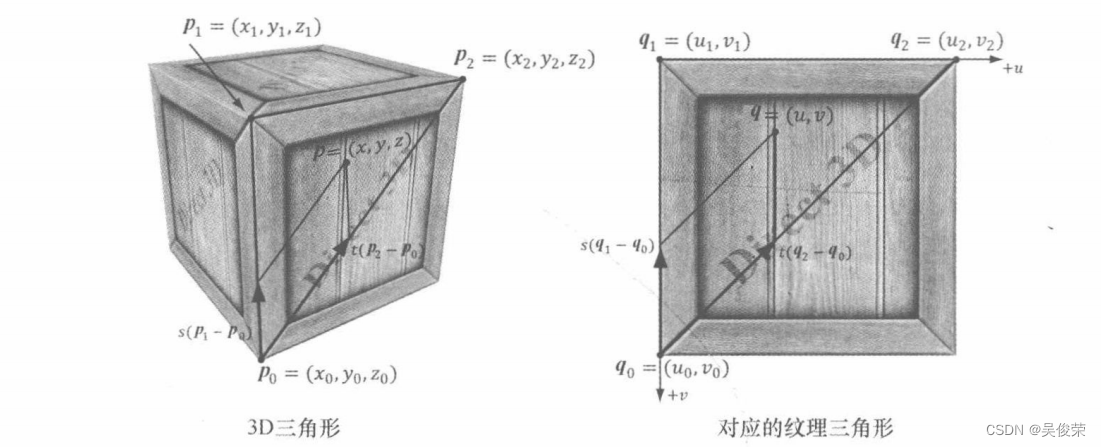
Direct3D 12——纹理——纹理
纹理不同于缓冲区资源,因为缓冲区资源仅存储数据数组,而纹理却可以具有多个mipmap层级(后 文有介绍),GPU会基于这个层级进行相应的特殊操作,例如运用过滤器以及多重采样。支持这些特殊 的操作纹理资源都被限定为一些特定的数据格式…...

产品经理必读 | 俞军产品经理十二条军规
最近在学习《俞军产品方法论》,觉得俞军总结的十二条产品经理原则非常受用,分享给大家。 01. 产品经理首先是产品的深度用户 自己设计的产品都没使用过的产品经理,如何明白用户使用的问题,如何解决问题,所以产品经理肯…...
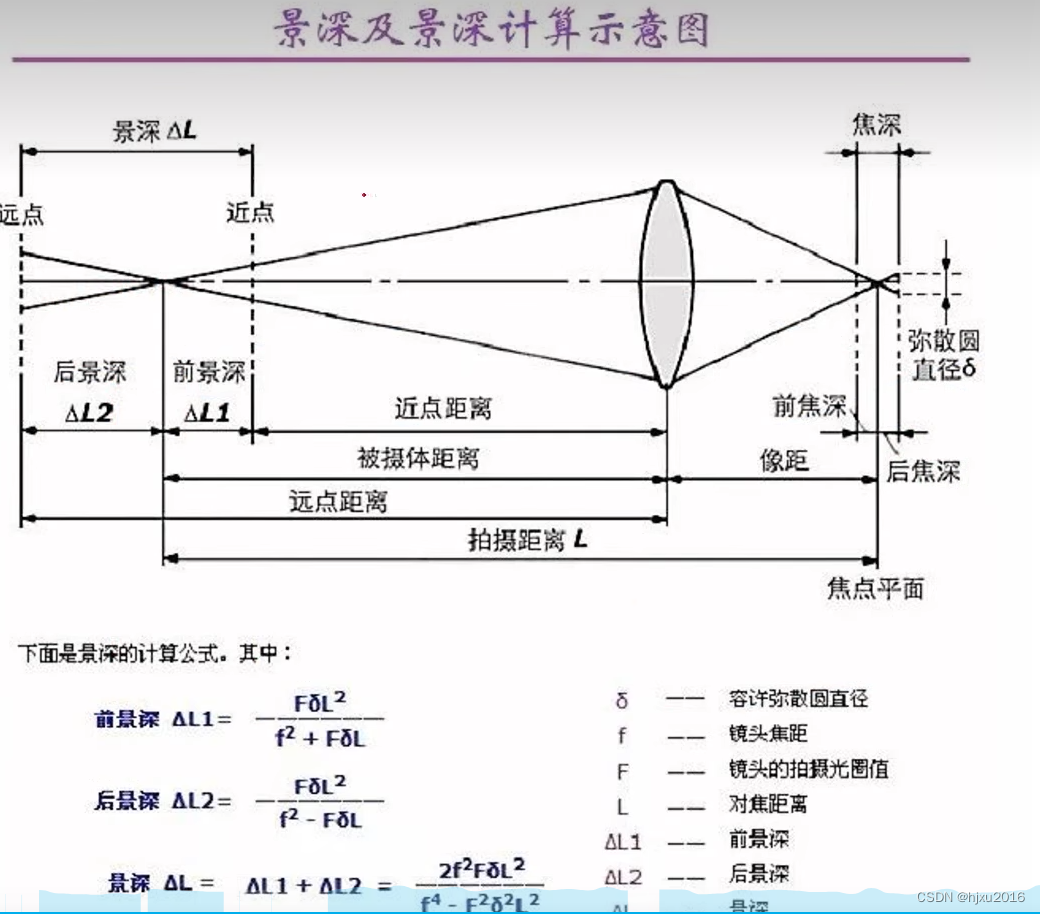
【机器视觉1】光源介绍与选择
文章目录一、常见照明光源类型二、照明光源对比三、照明技术3.1 亮视野与暗视野3.2 低角度照明3.3 前向光直射照明3.4 前向光漫射照明3.5 背光照明-测量系统的最佳选择3.6 颜色与补色示例3.7 偏光技术应用四、镜头4.1 镜头的几个概念4.2 影响图像质量的关键因素4.3 成像尺寸4.4…...

【三十天精通Vue 3】第十一天 Vue 3 过渡和动画详解
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录引言一、Vue 3 过度和动画概述1.1过度和动画的简介二、Vue 3 过度2…...
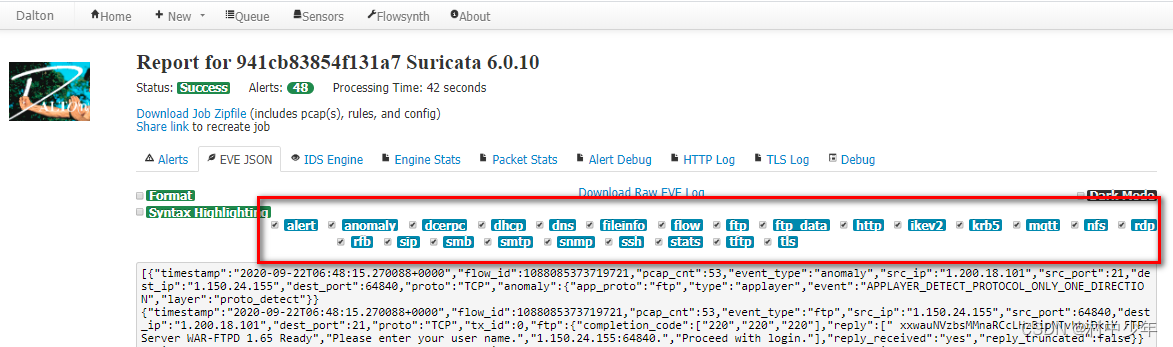
基于多种流量检测引擎识别pcap数据包中的威胁
在很多的场景下,会需要根据数据包判断数据包中存在的威胁。针对已有的数据包,如何判断数据包是何种攻击呢? 方法一可以根据经验,对于常见的WEB类型的攻击,比如SQL注入,命令执行等攻击,是比较容…...
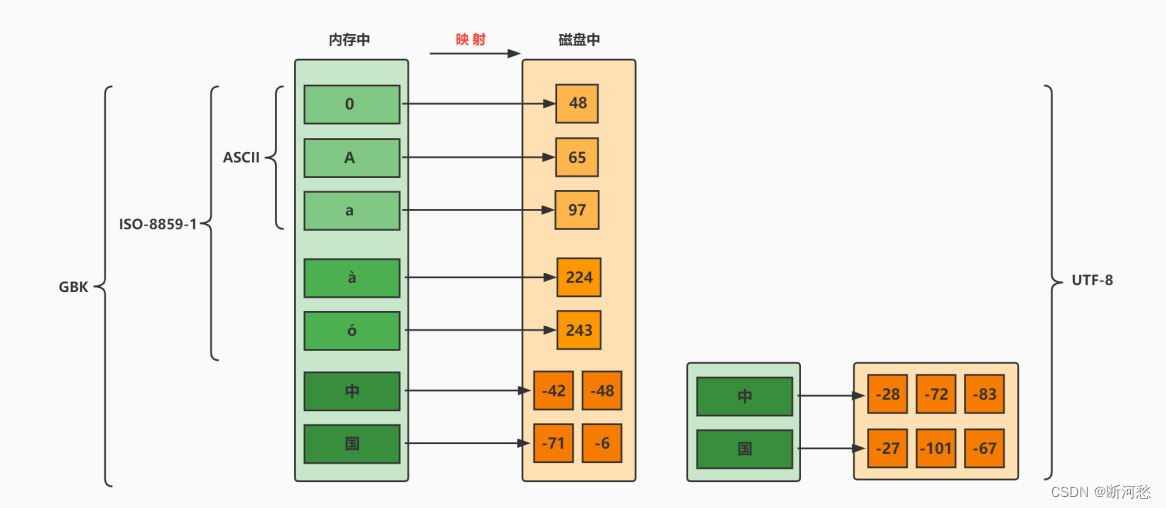
第02章_变量与运算符
第02章_变量与运算符 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 本章专题与脉络 1. 关键字(keyword) 定义:被Java语言赋予了特殊含义,用做专门…...

仅三行就能学会数据分析——Sweetviz详解
文章目录前言一、准备二、sweetviz 基本用法1.引入库2.读入数据3.调整报告布局总结前言 Sweetviz是一个开源Python库,它只需三行代码就可以生成漂亮的高精度可视化效果来启动EDA(探索性数据分析)。输出一个HTML。 如上图所示,它不仅能根据性别、年龄等…...

springboot——集成elasticsearch进行搜索并高亮关键词
目录 1.elasticsearch概述 3.springboot集成elasticsearch 4.实现搜索并高亮关键词 1.elasticsearch概述 (1)是什么: Elasticsearch 是位于 Elastic Stack 核心的分布式搜索和分析引擎。 Lucene 可以被认为是迄今为止最先进、性能最好的…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
