优先、双端队列-我的基础算法刷题之路(八)

本篇博客旨在整理记录自已对优先队列、双端队列的一些总结,以及刷题的解题思路,同时希望可给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉 💪。
本篇内容接上篇:http://t.csdn.cn/akLoF
文章目录
- 一、双端队列
- 1.概述
- 2.接口定义
- 3.代码实现
- 二、优先级队列
- 1.无序数组实现
- 2.有序数组实现
- 3.堆实现
- 三、阻塞队列
- 1.单锁实现
- 2.双锁实现
- 最后
一、双端队列
1.概述
对比如图:
| 定义 | 特点 | |
|---|---|---|
| 队列 | 一端删除(头)另一端添加(尾) | First In First Out |
| 双端队列 | 两端都可以删除、添加 | |
| 优先队列 | 优先级高者先出队 | |
| 延时队列 | 根据延时时间确定优先级 | |
| 并发非阻塞队列 | 队列空或满时不阻塞 | |
| 并发阻塞队列 | 队列空时删除阻塞、队列满时添加阻塞 |
注1:
- Java 中 LinkedList 即为典型双端队列实现,不过它同时实现了Queue 接口,也提供了栈的 push pop等方法
注2:
不同语言,操作双端队列得方法命名有所不同,见下表
操作 Java JavaScript C++ leetCode641 尾部插入 offerLast push push_back insertLast 头部插入 offerFirst unshift push_front insertFront 尾部移除 pollLast pop pop_back deleteLast 头部移除 pollFirst shift pop_front deleteFront 尾部获取 peekLast at(-1) back getRear 头部获取 peekFirst at(0) front getFront
- 常见的还有enqueue 入队、dequeue 出队
2.接口定义
public interface Deque<E> {boolean offerFirst(E e);boolean offerLast(E e);E pollFirst();E pollLast();E peekFirst();E peekLast();boolean isEmpty();boolean isFull();
}
3.代码实现
链表实现
/*** 基于环形链表的双端队列* @param <E> 元素类型*/
public class LinkedListDeque<E> implements Deque<E>, Iterable<E> {@Overridepublic boolean offerFirst(E e) {if (isFull()) {return false;}size++;Node<E> a = sentinel;Node<E> b = sentinel.next;Node<E> offered = new Node<>(a, e, b);a.next = offered;b.prev = offered;return true;}@Overridepublic boolean offerLast(E e) {if (isFull()) {return false;}size++;Node<E> a = sentinel.prev;Node<E> b = sentinel;Node<E> offered = new Node<>(a, e, b);a.next = offered;b.prev = offered;return true;}@Overridepublic E pollFirst() {if (isEmpty()) {return null;}Node<E> a = sentinel;Node<E> polled = sentinel.next;Node<E> b = polled.next;a.next = b;b.prev = a;size--;return polled.value;}@Overridepublic E pollLast() {if (isEmpty()) {return null;}Node<E> polled = sentinel.prev;Node<E> a = polled.prev;Node<E> b = sentinel;a.next = b;b.prev = a;size--;return polled.value;}@Overridepublic E peekFirst() {if (isEmpty()) {return null;}return sentinel.next.value;}@Overridepublic E peekLast() {if (isEmpty()) {return null;}return sentinel.prev.value;}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == capacity;}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {Node<E> p = sentinel.next;@Overridepublic boolean hasNext() {return p != sentinel;}@Overridepublic E next() {E value = p.value;p = p.next;return value;}};}static class Node<E> {Node<E> prev;E value;Node<E> next;public Node(Node<E> prev, E value, Node<E> next) {this.prev = prev;this.value = value;this.next = next;}}Node<E> sentinel = new Node<>(null, null, null);int capacity;int size;public LinkedListDeque(int capacity) {sentinel.next = sentinel;sentinel.prev = sentinel;this.capacity = capacity;}
}
数组实现
/*** 基于循环数组实现, 特点* <ul>* <li>tail 停下来的位置不存储, 会浪费一个位置</li>* </ul>* @param <E>*/
public class ArrayDeque1<E> implements Deque<E>, Iterable<E> {/*ht0 1 2 3b a*/@Overridepublic boolean offerFirst(E e) {if (isFull()) {return false;}head = dec(head, array.length);array[head] = e;return true;}@Overridepublic boolean offerLast(E e) {if (isFull()) {return false;}array[tail] = e;tail = inc(tail, array.length);return true;}@Overridepublic E pollFirst() {if (isEmpty()) {return null;}E e = array[head];array[head] = null;head = inc(head, array.length);return e;}@Overridepublic E pollLast() {if (isEmpty()) {return null;}tail = dec(tail, array.length);E e = array[tail];array[tail] = null;return e;}@Overridepublic E peekFirst() {if (isEmpty()) {return null;}return array[head];}@Overridepublic E peekLast() {if (isEmpty()) {return null;}return array[dec(tail, array.length)];}@Overridepublic boolean isEmpty() {return head == tail;}@Overridepublic boolean isFull() {if (tail > head) {return tail - head == array.length - 1;} else if (tail < head) {return head - tail == 1;} else {return false;}}@Overridepublic Iterator<E> iterator() {return new Iterator<E>() {int p = head;@Overridepublic boolean hasNext() {return p != tail;}@Overridepublic E next() {E e = array[p];p = inc(p, array.length);return e;}};}E[] array;int head;int tail;@SuppressWarnings("unchecked")public ArrayDeque1(int capacity) {array = (E[]) new Object[capacity + 1];}static int inc(int i, int length) {if (i + 1 >= length) {return 0;}return i + 1;}static int dec(int i, int length) {if (i - 1 < 0) {return length - 1;}return i - 1;}
}
数组实现中,如果存储的时基本类型,那么无需考虑内存释放,例如

但如果存储的是引用类型,应当设置该位置得引用为null,以便内存及时释放

二、优先级队列
1.无序数组实现
要点
- 入队保持顺序
- 出队前找到优先级最高的出队,相当于一次选择排序
public class PriorityQueue1<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue1(int capacity) {array = new Priority[capacity];}@Override // O(1)public boolean offer(E e) {if (isFull()) {return false;}array[size++] = e;return true;}// 返回优先级最高的索引值private int selectMax() {int max = 0;for (int i = 1; i < size; i++) {if (array[i].priority() > array[max].priority()) {max = i;}}return max;}@Override // O(n)public E poll() {if (isEmpty()) {return null;}int max = selectMax();E e = (E) array[max];remove(max);return e;}private void remove(int index) {if (index < size - 1) {System.arraycopy(array, index + 1,array, index, size - 1 - index);}array[--size] = null; // help GC}@Overridepublic E peek() {if (isEmpty()) {return null;}int max = selectMax();return (E) array[max];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
2.有序数组实现
要点
- 入队后排好序,优先级最高的排列在尾部
- 出队只需删除尾部元素即可
public class PriorityQueue2<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue2(int capacity) {array = new Priority[capacity];}// O(n)@Overridepublic boolean offer(E e) {if (isFull()) {return false;}insert(e);size++;return true;}// 一轮插入排序private void insert(E e) {int i = size - 1;while (i >= 0 && array[i].priority() > e.priority()) {array[i + 1] = array[i];i--;}array[i + 1] = e;}// O(1)@Overridepublic E poll() {if (isEmpty()) {return null;}E e = (E) array[size - 1];array[--size] = null; // help GCreturn e;}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[size - 1];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
3.堆实现
计算机科学中,堆是一种基于树的数据结构,通常用完全二叉树实现。堆的特性如下
- 在大顶堆中,任意节点 C 与它的父节点 P 符合 P.value≥C.valueP.value \geq C.valueP.value≥C.value
- 而小顶堆中,任意节点 C 与它的父节点 P 符合 P.value≤C.valueP.value \leq C.valueP.value≤C.value
- 最顶层的节点(没有父亲)称之为 root 根节点
例1 - 满二叉树(Full Binary Tree)特点:每一层都是填满的

例2 - 完全二叉树(Complete Binary Tree)特点:最后一层可能未填满,靠左对齐

例3 - 大顶堆

例4 - 小顶堆

完全二叉树可以使用数组来表示

特征
- 如果从索引 0 开始存储节点数据
- 节点 i 的父结点为 floor((i−1)/2)floor((i-1)/2)floor((i−1)/2),当i>0i > 0i>0时
- 节点 i 的左子节点为 2i+12i+12i+1,右子节点为2i+22i+22i+2,当然它们得 <size< size<size
- 如果从索引 1 开始存储节点数据
- 节点 iii 的父结点为 floor(i/2)floor(i/2)floor(i/2),当 i>1i>1i>1 时
- 节点 iii 的左子节点为 2i2i2i,右子节点为 2i+12i+12i+1,同样得 <size< size<size
代码
public class PriorityQueue4<E extends Priority> implements Queue<E> {Priority[] array;int size;public PriorityQueue4(int capacity) {array = new Priority[capacity];}@Overridepublic boolean offer(E offered) {if (isFull()) {return false;}int child = size++;int parent = (child - 1) / 2;while (child > 0 && offered.priority() > array[parent].priority()) {array[child] = array[parent];child = parent;parent = (child - 1) / 2;}array[child] = offered;return true;}private void swap(int i, int j) {Priority t = array[i];array[i] = array[j];array[j] = t;}@Overridepublic E poll() {if (isEmpty()) {return null;}swap(0, size - 1);size--;Priority e = array[size];array[size] = null;shiftDown(0); return (E) e;}void shiftDown(int parent) {int left = 2 * parent + 1;int right = left + 1;int max = parent;if (left < size && array[left].priority() > array[max].priority()) {max = left;}if (right < size && array[right].priority() > array[max].priority()) {max = right;}if (max != parent) {swap(max, parent);shiftDown(max);}}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E) array[0];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == array.length;}
}
三、阻塞队列
之前的队列在很多场景下都不能很好地工作,例如
- 大部分场景要求分离向队列放入(生产者)、从队列拿出(消费者)两个角色、它们得由不同的线程来担当,而之前的实现根本没有考虑线程安全问题
- 队列为空,那么在之前的实现里会返回 null,如果就是硬要拿到一个元素呢?只要不断循环尝试
- 队列为满,那么再之前的实现里会返回 false,如果就是硬要塞入一个元素呢?只能不断循环尝试
因此我们需要解决的问题有
- 用锁保证线程的安全
- 用条件变量让等待非空线程与等待不满线程进入等待状态,而不是不断循环尝试,让 CPU 空转
有同学对线程安全还没有足够的认识,下面举一个反例,两个线程都要执行入队操作(几乎在同一时刻)
public class TestThreadUnsafe {private final String[] array = new String[10];private int tail = 0;public void offer(String e) {array[tail] = e;tail++;}@Overridepublic String toString() {return Arrays.toString(array);}public static void main(String[] args) {TestThreadUnsafe queue = new TestThreadUnsafe();new Thread(()-> queue.offer("e1"), "t1").start();new Thread(()-> queue.offer("e2"), "t2").start();}
}
执行的时间序列如下,假设初始状态 tail = 0,在执行过程中由于 CPU 在两个线程之间切换,造成了指令交错。
| 线程1 | 线程2 | 说明 |
|---|---|---|
| array[tail]=e1 | 线程1 向 tail 位置加入 e1 这个元素,但还没来得及执行 tail++ | |
| array[tail]=e2 | 线程2 向 tail 位置加入 e2 这个元素,覆盖掉了 e1 | |
| tail++ | tail 自增为1 | |
| tail++ | tail 自增为2 | |
| 最后状态 tail 为 2,数组为 [e2, null, null …] |
糟糕的是,由于指令交错的顺序不同,得到的结果不止以上一种,宏观上造成混乱的效果。
1.单锁实现
Java 中要防止代码段交错执行,需要使用锁,有两种选择
- synchronized 代码块,属于关键字级别提供锁保护,功能少
- ReentrantLock 类,功能丰富
以 ReentrantLock 为例
ReentrantLock lock = new ReentrantLock();public void offer(String e) {lock.lockInterruptibly();try {array[tail] = e;tail++;} finally {lock.unlock();}
}
只要两个线程执行上段代码时,锁对象是同一个,就能保证 try 块内的代码的执行不会出现指令交错现象,即执行顺序只可能是下面两种情况之一。
| 线程1 | 线程2 | 说明 |
|---|---|---|
| lock.lockInterruptibly() | t1对锁对象上锁 | |
| array[tail]=e1 | ||
| lock.lockInterruptibly() | 即使 CPU 切换到线程2,但由于t1已经对该对象上锁,因此线程2卡在这儿进不去 | |
| tail++ | 切换回线程1 执行后续代码 | |
| lock.unlock() | 线程1 解锁 | |
| array[tail]=e2 | 线程2 此时才能获得锁,执行它的代码 | |
| tail++ |
- 另一种情况是线程2 先获得锁,线程1 被挡在外面
- 要明白保护的本质,本例中是保护的是 tail 位置读写的安全
事情还没有完,上面的例子是队列还没有放满的情况,考虑下面的代码(这回锁同时保护了 tail 和 size 的读写安全)
ReentrantLock lock = new ReentrantLock();
int size = 0;public void offer(String e) {lock.lockInterruptibly();try {if(isFull()) {// 满了怎么办?}array[tail] = e;tail++;size++;} finally {lock.unlock();}
}private boolean isFull() {return size == array.length;
}
之前是返回 false 表示添加失败,前面分析过想达到这么一种效果:
- 在队列满时,不是立刻返回,而是当前线程进入等待
- 什么时候队列不满了,再唤醒这个等待的线程,从上次的代码处继续向下运行
ReentrantLock 可以配合条件变量来实现,代码进化为:
ReentrantLock lock = new ReentrantLock();
Condition tailWaits = lock.newCondition(); // 条件变量
int size = 0;public void offer(String e) {lock.lockInterruptibly();try {while (isFull()) {tailWaits.await(); // 当队列满时, 当前线程进入 tailWaits 等待}array[tail] = e;tail++;size++;} finally {lock.unlock();}
}private boolean isFull() {return size == array.length;
}
- 条件变量底层也是个队列,用来存储这些需要等待的线程,当队列满了,就会将 offer 线程加入条件队列,并暂时释放锁
- 将来我们的队列如果不满了(由 poll 线程那边得知)可以调用 tailWaits.signal() 来唤醒 tailWaits 中首个等待的线程,被唤醒的线程会再次抢到锁,从上次 await 处继续向下运行
思考为何要用 while 而不是 if,设队列容量是 3?
| 操作前 | offer(4) | offer(5) | poll() | 操作后 |
|---|---|---|---|---|
| [1 2 3] | 队列满,进入tailWaits 等待 | [1 2 3] | ||
| [1 2 3] | 取走 1,队列不满,唤醒线程 | [2 3] | ||
| [2 3] | 抢先获得锁,发现不满,放入 5 | [2 3 5] | ||
| [2 3 5] | 从上次等待处直接向下执行 | [2 3 5 ?] |
关键点:
- 从 tailWaits 中唤醒的线程,会与新来的 offer 的线程争抢锁,谁能抢到是不一定的,如果后者先抢到,就会导致条件又发生变化
- 这种情况称之为虚假唤醒,唤醒后应该重新检查条件,看是不是得重新进入等待
最后的实现代码
/*** 单锁实现* @param <E> 元素类型*/
public class BlockingQueue1<E> implements BlockingQueue<E> {private final E[] array;private int head = 0;private int tail = 0;private int size = 0; // 元素个数@SuppressWarnings("all")public BlockingQueue1(int capacity) {array = (E[]) new Object[capacity];}ReentrantLock lock = new ReentrantLock();Condition tailWaits = lock.newCondition();Condition headWaits = lock.newCondition();@Overridepublic void offer(E e) throws InterruptedException {lock.lockInterruptibly();try {while (isFull()) {tailWaits.await();}array[tail] = e;if (++tail == array.length) {tail = 0;}size++;headWaits.signal();} finally {lock.unlock();}}@Overridepublic void offer(E e, long timeout) throws InterruptedException {lock.lockInterruptibly();try {long t = TimeUnit.MILLISECONDS.toNanos(timeout);while (isFull()) {if (t <= 0) {return;}t = tailWaits.awaitNanos(t);}array[tail] = e;if (++tail == array.length) {tail = 0;}size++;headWaits.signal();} finally {lock.unlock();}}@Overridepublic E poll() throws InterruptedException {lock.lockInterruptibly();try {while (isEmpty()) {headWaits.await();}E e = array[head];array[head] = null; // help GCif (++head == array.length) {head = 0;}size--;tailWaits.signal();return e;} finally {lock.unlock();}}private boolean isEmpty() {return size == 0;}private boolean isFull() {return size == array.length;}
}
- public void offer(E e, long timeout) throws InterruptedException 是带超时的版本,可以只等待一段时间,而不是永久等下去,类似的 poll 也可以做带超时的版本,这个留给大家了。
注意
- JDK 中 BlockingQueue 接口的方法命名与我的示例有些差异
- 方法 offer(E e) 是非阻塞的实现,阻塞实现方法为 put(E e)
- 方法 poll() 是非阻塞的实现,阻塞实现方法为 take()
2.双锁实现
单锁的缺点在于:
- 生产和消费几乎是不冲突的,唯一冲突的是生产者和消费者它们有可能同时修改 size
- 冲突的主要是生产者之间:多个 offer 线程修改 tail
- 冲突的还有消费者之间:多个 poll 线程修改 head
如果希望进一步提高性能,可以用两把锁:
- 一把锁保护 tail
- 另一把锁保护 head
ReentrantLock headLock = new ReentrantLock(); // 保护 head 的锁
Condition headWaits = headLock.newCondition(); // 队列空时,需要等待的线程集合ReentrantLock tailLock = new ReentrantLock(); // 保护 tail 的锁
Condition tailWaits = tailLock.newCondition(); // 队列满时,需要等待的线程集合
先看看 offer 方法的初步实现
@Override
public void offer(E e) throws InterruptedException {tailLock.lockInterruptibly();try {// 队列满等待while (isFull()) {tailWaits.await();}// 不满则入队array[tail] = e;if (++tail == array.length) {tail = 0;}// 修改 size (有问题)size++;} finally {tailLock.unlock();}
}
上面代码的缺点是 size 并不受 tailLock 保护,tailLock 与 headLock 是两把不同的锁,并不能实现互斥的效果。因此,size 需要用下面的代码保证原子性。
AtomicInteger size = new AtomicInteger(0); // 保护 size 的原子变量size.getAndIncrement(); // 自增
size.getAndDecrement(); // 自减
代码修改为
@Override
public void offer(E e) throws InterruptedException {tailLock.lockInterruptibly();try {// 队列满等待while (isFull()) {tailWaits.await();}// 不满则入队array[tail] = e;if (++tail == array.length) {tail = 0;}// 修改 sizesize.getAndIncrement();} finally {tailLock.unlock();}
}
对称地,可以写出 poll 方法
@Override
public E poll() throws InterruptedException {E e;headLock.lockInterruptibly();try {// 队列空等待while (isEmpty()) {headWaits.await();}// 不空则出队e = array[head];if (++head == array.length) {head = 0;}// 修改 sizesize.getAndDecrement();} finally {headLock.unlock();}return e;
}
下面来看一个难题,就是如何通知 headWaits 和 tailWaits 中等待的线程,比如 poll 方法拿走一个元素,通知 tailWaits:我拿走一个,不满了噢,你们可以放了,因此代码改为
@Override
public E poll() throws InterruptedException {E e;headLock.lockInterruptibly();try {// 队列空等待while (isEmpty()) {headWaits.await();}// 不空则出队e = array[head];if (++head == array.length) {head = 0;}// 修改 sizesize.getAndDecrement();// 通知 tailWaits 不满(有问题)tailWaits.signal();} finally {headLock.unlock();}return e;
}
问题在于要使用这些条件变量的 await(), signal() 等方法需要先获得与之关联的锁,上面的代码若直接运行会出现以下错误:
java.lang.IllegalMonitorStateException
那有同学说,加上锁不就行了吗,于是写出了下面的代码
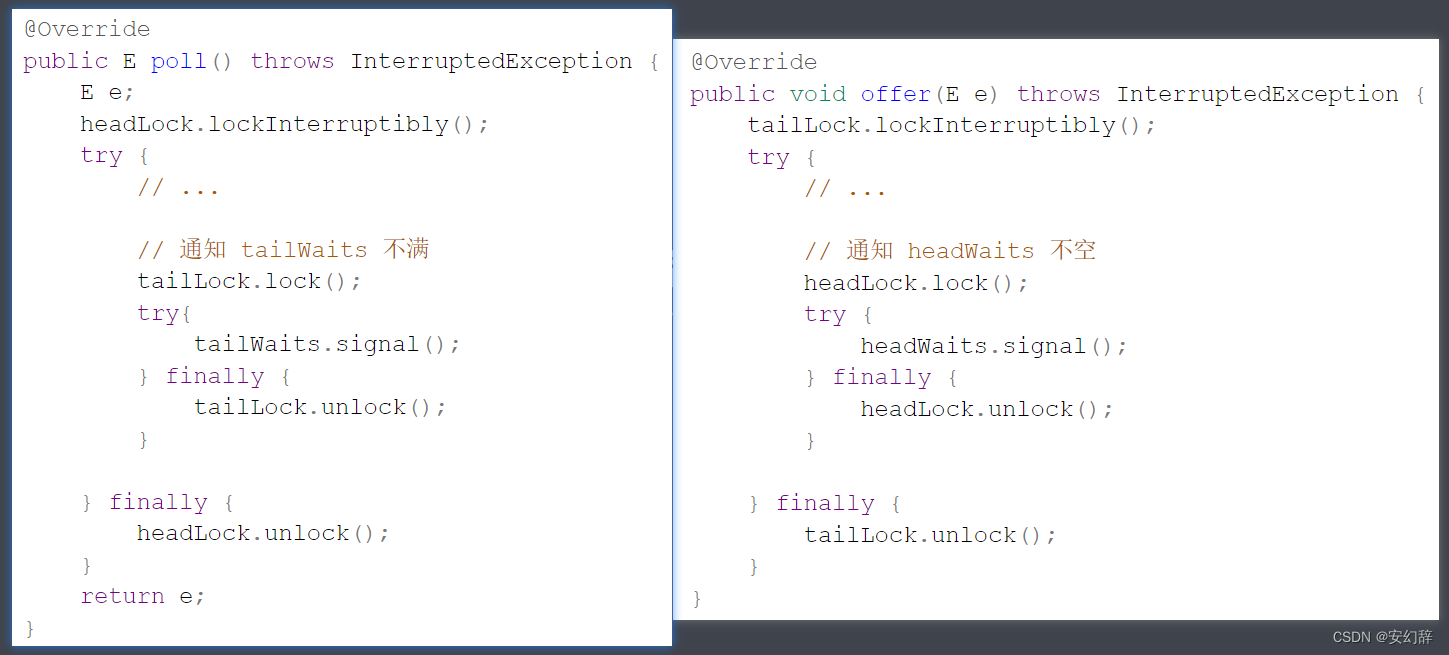
发现什么问题了?两把锁这么嵌套使用,非常容易出现死锁,如下所示

因此得避免嵌套,两段加锁的代码变成了下面平级的样子

性能还可以进一步提升
-
代码调整后 offer 并没有同时获取 tailLock 和 headLock 两把锁,因此两次加锁之间会有空隙,这个空隙内可能有其它的 offer 线程添加了更多的元素,那么这些线程都要执行 signal(),通知 poll 线程队列非空吗?
- 每次调用 signal() 都需要这些 offer 线程先获得 headLock 锁,成本较高,要想法减少 offer 线程获得 headLock 锁的次数
- 可以加一个条件:当 offer 增加前队列为空,即从 0 变化到不空,才由此 offer 线程来通知 headWaits,其它情况不归它管
-
队列从 0 变化到不空,会唤醒一个等待的 poll 线程,这个线程被唤醒后,肯定能拿到 headLock 锁,因此它具备了唤醒 headWaits 上其它 poll 线程的先决条件。如果检查出此时有其它 offer 线程新增了元素(不空,但不是从0变化而来),那么不妨由此 poll 线程来唤醒其它 poll 线程
这个技巧被称之为级联通知(cascading notifies),类似的原因
- 在 poll 时队列从满变化到不满,才由此 poll 线程来唤醒一个等待的 offer 线程,目的也是为了减少 poll 线程对 tailLock 上锁次数,剩下等待的 offer 线程由这个 offer 线程间接唤醒
最终的代码为
public class BlockingQueue2<E> implements BlockingQueue<E> {private final E[] array;private int head = 0;private int tail = 0;private final AtomicInteger size = new AtomicInteger(0);ReentrantLock headLock = new ReentrantLock();Condition headWaits = headLock.newCondition();ReentrantLock tailLock = new ReentrantLock();Condition tailWaits = tailLock.newCondition();public BlockingQueue2(int capacity) {this.array = (E[]) new Object[capacity];}@Overridepublic void offer(E e) throws InterruptedException {int c;tailLock.lockInterruptibly();try {while (isFull()) {tailWaits.await();}array[tail] = e;if (++tail == array.length) {tail = 0;} c = size.getAndIncrement();// a. 队列不满, 但不是从满->不满, 由此offer线程唤醒其它offer线程if (c + 1 < array.length) {tailWaits.signal();}} finally {tailLock.unlock();}// b. 从0->不空, 由此offer线程唤醒等待的poll线程if (c == 0) {headLock.lock();try {headWaits.signal();} finally {headLock.unlock();}}}@Overridepublic E poll() throws InterruptedException {E e;int c;headLock.lockInterruptibly();try {while (isEmpty()) {headWaits.await(); }e = array[head]; if (++head == array.length) {head = 0;}c = size.getAndDecrement();// b. 队列不空, 但不是从0变化到不空,由此poll线程通知其它poll线程if (c > 1) {headWaits.signal();}} finally {headLock.unlock();}// a. 从满->不满, 由此poll线程唤醒等待的offer线程if (c == array.length) {tailLock.lock();try {tailWaits.signal();} finally {tailLock.unlock();}}return e;}private boolean isEmpty() {return size.get() == 0;}private boolean isFull() {return size.get() == array.length;}}
最后
对各位小伙伴有帮助的话,希望可以点赞❤️+收藏⭐,谢谢各位大佬~~🙌🙌🙌
相关文章:

优先、双端队列-我的基础算法刷题之路(八)
本篇博客旨在整理记录自已对优先队列、双端队列的一些总结,以及刷题的解题思路,同时希望可给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉 &…...
 方法、Python 质数判断)
Python3 os.symlink() 方法、Python 质数判断
Python3 os.symlink() 方法 概述 os.symlink() 方法用于创建一个软链接。 语法 symlink()方法语法格式如下: os.symlink(src, dst)参数 src -- 源地址。 dst -- 目标地址。 返回值 该方法没有返回值。 实例 以下实例演示了 symlink() 方法的使用࿱…...

P1972 [SDOI2009] HH的项链
[SDOI2009] HH的项链 题目描述 HH 有一串由各种漂亮的贝壳组成的项链。HH 相信不同的贝壳会带来好运,所以每次散步完后,他都会随意取出一段贝壳,思考它们所表达的含义。HH 不断地收集新的贝壳,因此,他的项链变得越来…...
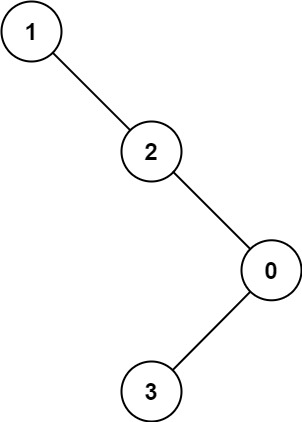
力扣解法汇总1026. 节点与其祖先之间的最大差值
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值…...
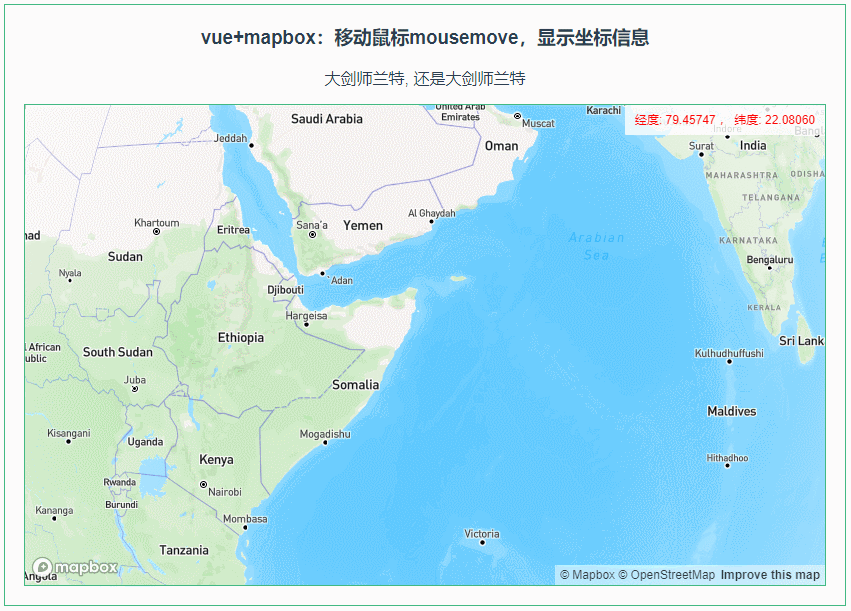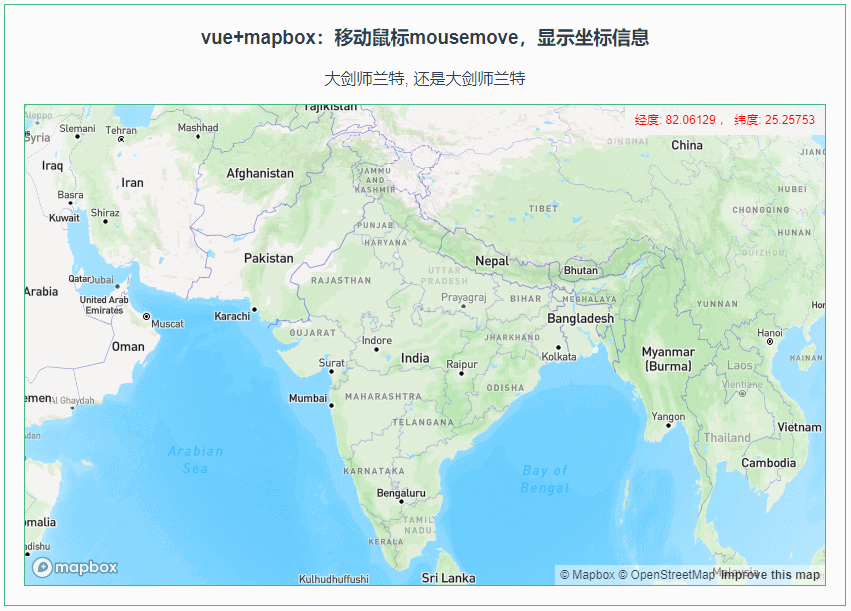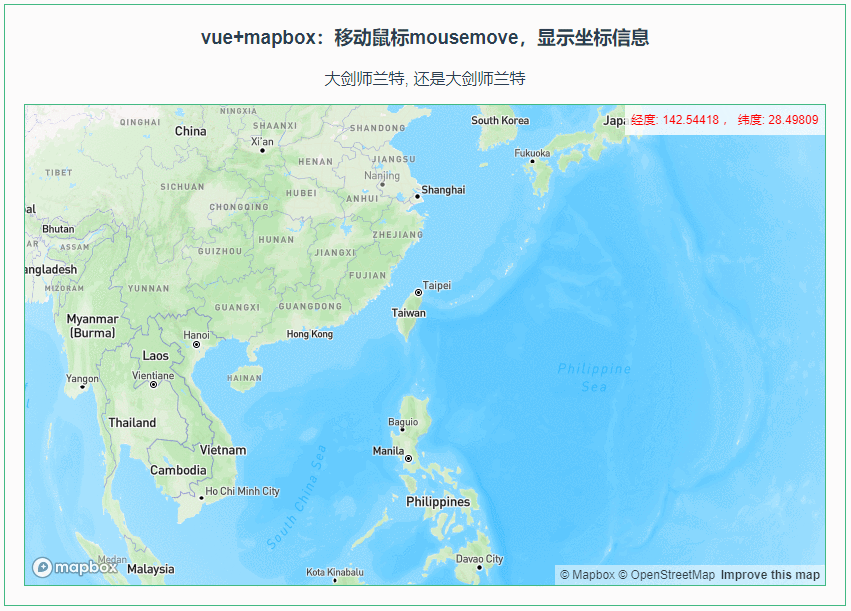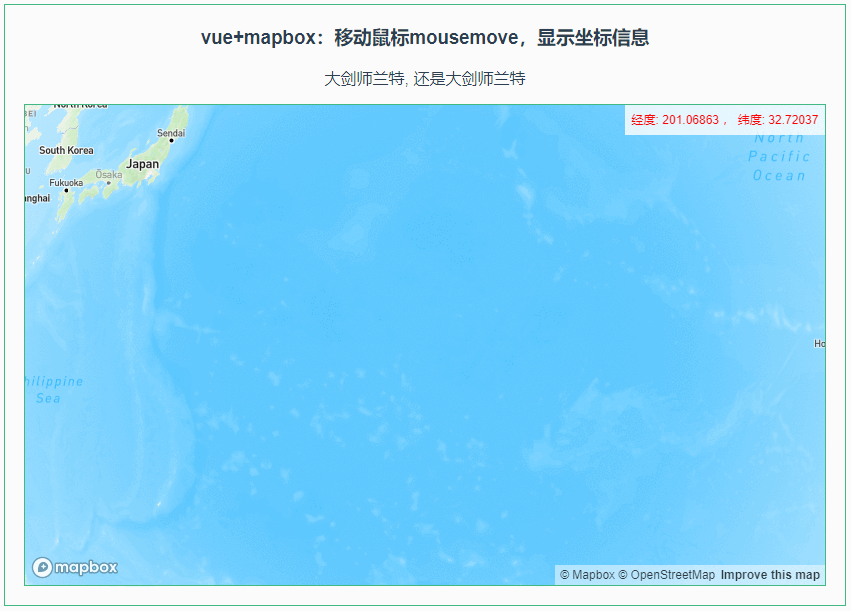
010:Mapbox GL移动鼠标mousemove,显示坐标信息
第010个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中移动鼠标mousemove,显示坐标信息。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共81行)相关API参考:专栏目标示例效果 配置方式 1)查看基础…...

【两阶段鲁棒优化】利用列-约束生成方法求解两阶段鲁棒优化问题(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

百度暑期实习 C++ 一面
1.数组 链表 数组是一种线性数据结构,其中相同类型的元素连续存储在一段内存中,并且可以通过索引来访问每个元素。数组的优点是随机访问元素非常快速,但缺点是插入或删除元素可能需要移动其他元素。 链表也是一种线性数据结构,但…...

计算机网络第一章(概述)【湖科大教书匠】
1. 各种网络 网络(Network)由若干**结点(Node)和连接这些结点的链路(Link)**组成多个网络还可以通过路由器互连起来,这样就构成了一个覆盖范围更大的网络,即互联网(互连网)。因此,互联网是"网络的网络(Network of Networks)"**因特…...

【JS】vis.js使用之vis-timeline使用攻略,vis-timeline在vue3中实现时间轴、甘特图
vis.js使用之vis-timeline使用攻略,vis-timeline实现时间轴、甘特图1、vis-timeline简介2、安装插件及依赖3、简单示例4、疑难问题集合1. 中文zh-cn本地化2. 关于自定义class样式无法被渲染3. 关于双向数据绑定vis.js是一个基于浏览器的可视化库,它提供了…...

机器学习——数据处理
机器学习简介 机器学习是人工智能的一个实现途径深度学习是机器学习的一个方法发展而来 机器学习:从数据中自动分析获得模型,并利用模型对未知数据进行预测。 数据集的格式: 特征值目标值 比如上图中房子的各种属性是特征值,然…...
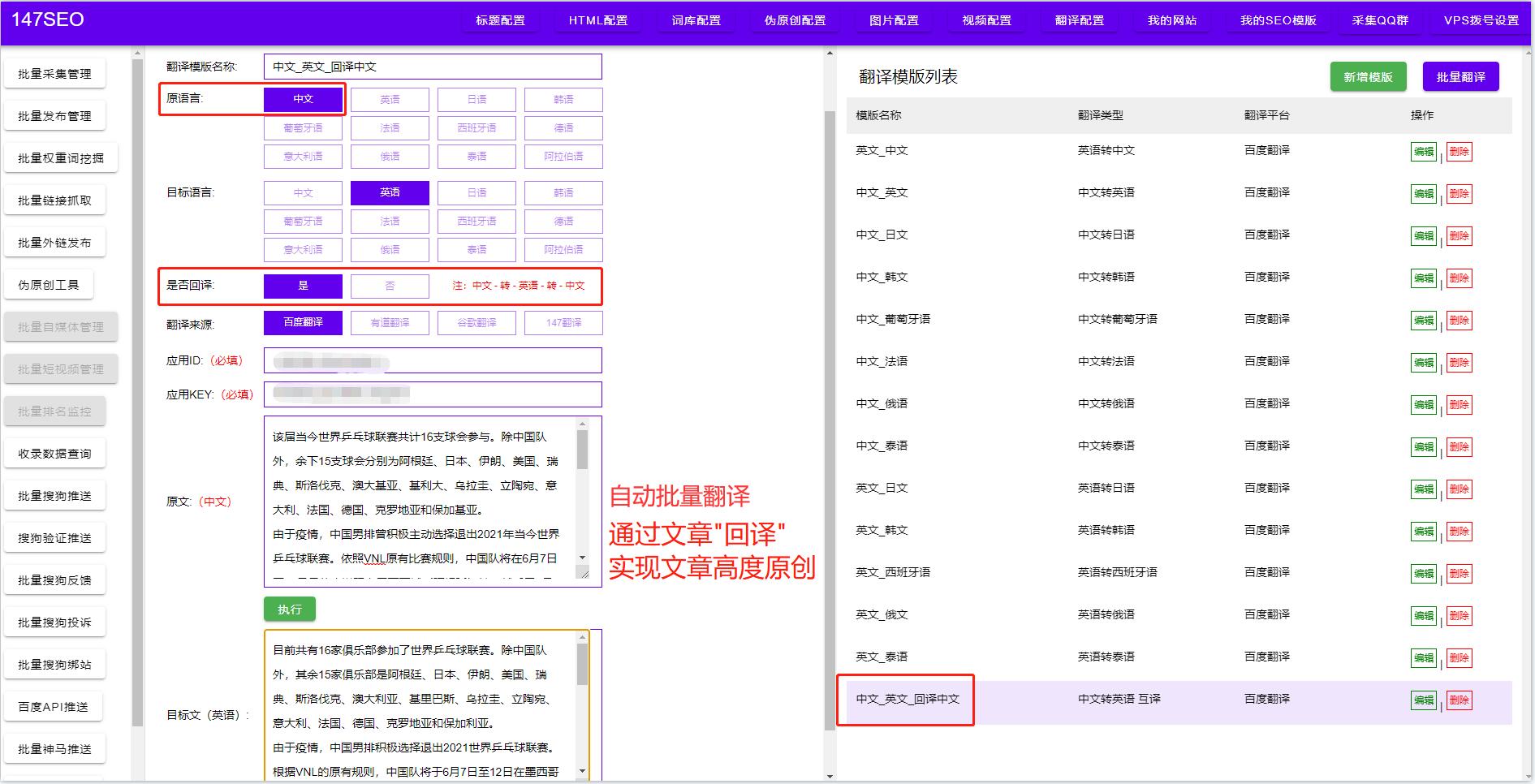
多种文字翻译软件-翻译常用软件
整篇文档翻译软件 整篇文档翻译软件是一种实现全文翻译的自动翻译工具,它能够快速、准确地将整篇文档的内容翻译成目标语言。与单词、句子翻译不同,整篇文档翻译软件不仅需要具备准确的语言识别和翻译技术,还需要考虑上下文语境和文档格式等多…...
)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK将相机图像数据用二进制的方式保存到本地(C++)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK将相机图像数据用二进制的方式保存到本地(C)Baumer工业相机Baumer工业相机将图像保存为二进制图像的技术背景代码分析第一步:先转换Byte*图像为二进制图像第二步:在回调函数里进行Buf…...

JavaScript模块的导出和导入之export和module.exports的区别
export和module.exports (需要前面的export没有“s”,后面的module.exports 有“s”) 使用两者根本区别是 **exports **返回的是模块函数 **module.exports **返回的是模块对象本身,返回的是一个类 使用上的区别是exports的方法可以直接调用module.exports需要new…...
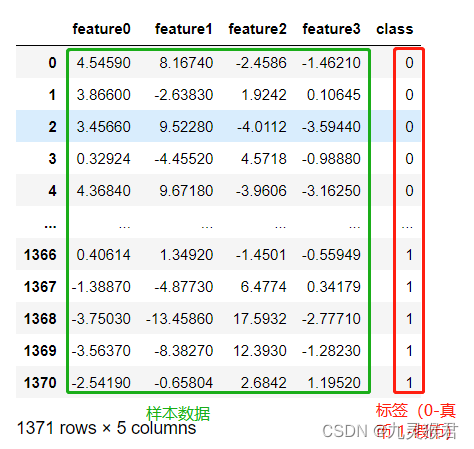
基于朴素贝叶斯分类器的钞票真伪识别模型
基于朴素贝叶斯分类器的钞票真伪识别模型 内容 本实验通过实现钞票真伪判别案例来展开学习朴素贝叶斯分类器的原理及应用。 本实验的主要技能点: 1、 朴素贝叶斯分类器模型的构建 2、 模型的评估与预测 3、 分类概率的输出 源码下载 环境 操作系统…...

【Python】【进阶篇】二十二、Python爬虫的BS4解析库
目录二十二、Python爬虫的BS4解析库22.1 BS4下载安装22.2 BS4解析对象22.3 BS4常用语法1) Tag节点22.4 遍历节点22.5 find_all()与find()1) find_all()2) find()22.6 CSS选择器二十二、Python爬虫的BS4解析库 Beautiful Soup 简称 BS4(其中 4 表示版本号࿰…...

UDS统一诊断服务【五】诊断仪在线0X3E服务
文章目录前言一、诊断仪在线服务介绍二、数据格式2.1,请求报文2.2,子功能2.3,响应报文前言 本文介绍UDS统一诊断服务的0X3E服务,希望能对你有所帮助 一、诊断仪在线服务介绍 诊断仪在线服务比较简单,其功能就是告诉服…...
我的创作纪念日:Unity CEO表示生成式AI将是Unity近期发展重点,发布神秘影片预告
PICK 未来的AI技术将会让人类迎来下一个生产力变革,这其中也包括生成型AI的突破性革新。各大公司也正在竞相推出AIGC工具,其中微软的Copilot、Adobe的Firefly、Github的chatGPT等引起了人们的关注。然而,游戏开发领域似乎还没有一款真正针对性…...

秩亏自由网平差的直接解法
目录 一、原理概述二、案例分析三、代码实现四、结果展示一、原理概述 N = B T P B N=B^TPB N=<...

大数据开发必备面试题Spark篇合集
1、Hadoop 和 Spark 的相同点和不同点? Hadoop 底层使用 MapReduce 计算架构,只有 map 和 reduce 两种操作,表达能力比较欠缺,而且在 MR 过程中会重复的读写 hdfs,造成大量的磁盘 io 读写操作,所以适合高时…...

C ++匿名函数:揭开C++ Lambda表达式的神秘面纱
潜意识编程:揭秘C Lambda表达式的神秘面纱 Subconscious Programming: Unveiling the Mystery of C Lambda Expressions 引言:Lambda表达式的魅力 (The Charm of C Lambda Expressions)Lambda表达式简介与基本概念 (Introduction and Basic Concepts of …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
