每日一题 leetcode1026 2023-4-18
1026. 节点与其祖先之间的最大差值
力扣题目链接
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例1:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0yEMB3qr-1681826098107)(image/leetcode1026/1681810158883.png)]](https://img-blog.csdnimg.cn/e43b7bf2a1264376b8e75d2ca14402bc.png)
输入:root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出:7
解释:
我们有大量的节点与其祖先的差值,其中一些如下:
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
示例2:
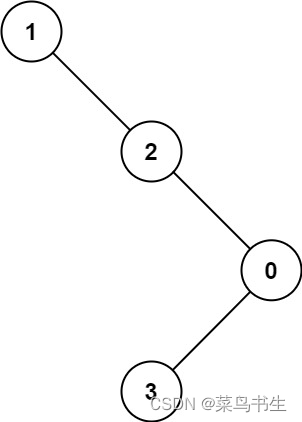
输入:root = [1,null,2,null,0,3]
输出:3
提示:
- 树中的节点数在
2到5000之间。 0 <= Node.val <= 10<sup>5</sup>
思路:
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number}*/
var maxAncestorDiff = function(root) {let diff = 0const diffData = (node,min,max) =>{if(!node) return 0diff = Math.max(Math.abs(node.val-min),Math.abs(node.val-max))min = Math.min(min,node.val)max = Math.max(max,node.val)diff = Math.max(diff,diffData(node.left,min,max)) diff = Math.max(diff,diffData(node.right,min,max)) return diff}return diffData(root,root.val,root.val)
};
总结:
复杂度
- 时间复杂度:O(n),其中n 是二叉树的节点数目。遍历二叉树的所有节点需要O(n)。
- 空间复杂度:O(n)。最坏情况下,二叉树退化为链表,递归栈的空间为O(n)。
更多详情看这里!
相关文章:

每日一题 leetcode1026 2023-4-18
1026. 节点与其祖先之间的最大差值 力扣题目链接 给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V |A.val - B.val|,且 A 是 B 的祖先。 (如果 A 的任何子节点之一为 B,或者 A 的任何…...

【Python_Scrapy学习笔记(十二)】基于Scrapy框架实现POST请求爬虫
基于Scrapy框架实现POST请求爬虫 前言 本文中介绍 如何基于 Scrapy 框架实现 POST 请求爬虫,并以抓取指定城市的 KFC 门店信息为例进行展示 正文 1、Scrapy框架处理POST请求方法 Scrapy框架 提供了 FormRequest() 方法来发送 POST 请求; FormReques…...

《花雕学AI》02:人工智能挺麻利,十分钟就为我写了一篇长长的故事
ChatGPT最近火爆全网,上线短短两个多月,活跃用户就过亿了,刷新了历史最火应用记录,网上几乎每天也都是ChatGPT各种消息。国内用户由于无法直接访问ChatGPT,所以大部分用户都无缘体验。不过呢,前段时间微软正…...

做程序员累了想要转行?我想给大家分享一下看法
今天早上起床时,我看到有粉丝评论说关于程序员的话题,如果做着觉得累了,就会觉得自己不适合这个工作,想转行。我想给大家分享一下我的看法。 在我刚开始工作时,有人说我不适合做这个工作,但是我坚持了下来…...
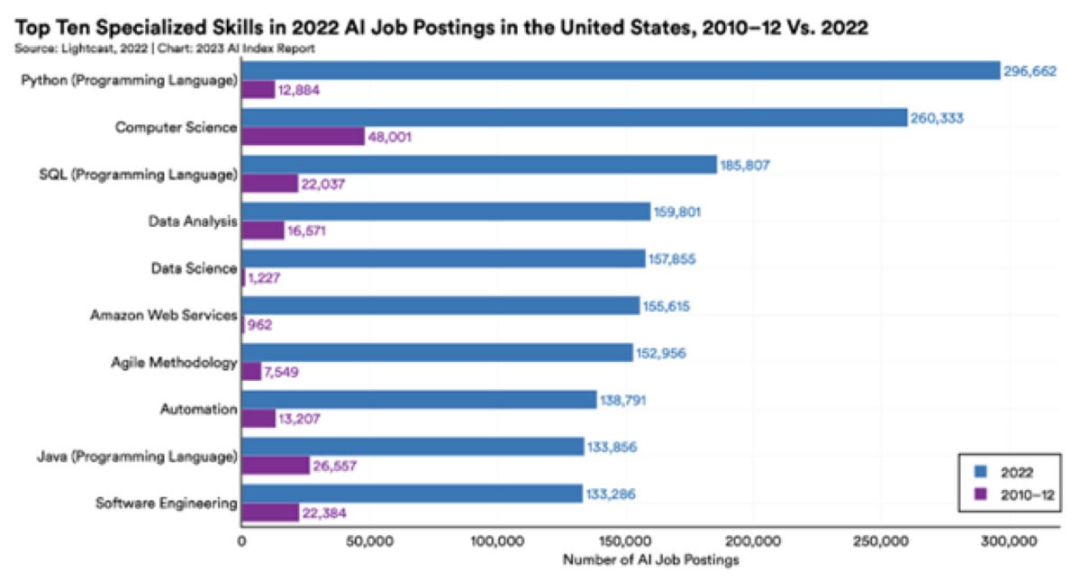
如果你想从事人工智能职业,学习Python吧
人工智能并不会抢走你的工作,至少目前还不会。人工智能和机器学习(AI/ML)最好的应用是补充人类的创造力,而不是取代它。具有讽刺意味的是,最好的大型语言模型(LLMs)可能是通过使用受版权保护的人…...

百模大战,谁是下一个ChatGPT?
“不敢下手,现在中国还没跑出来一家绝对有优势的大模型,上层应用没法投,担心押错宝。”投资人Jucy(化名)向光锥智能表示,AI项目看得多、投的少是这段时间的VC常态。 ChatGPT点燃AI大爆炸2个月中࿰…...

Revit中怎么绘制多面坡度的屋顶及生成墙
一、Revit中怎么绘制多面坡度的屋顶 像这种坡屋顶我们可以观察到,它的屋顶轮廓都是带有坡度的,那我可以通过添加定义坡度的方式来绘制出该屋顶。 点击建筑选项卡中的屋顶按钮,选择迹线屋顶。 选择使用拾取线工具,在选项栏中将偏…...

【jvm系列-07】深入理解执行引擎,解释器、JIT即时编译器
JVM系列整体栏目 内容链接地址【一】初识虚拟机与java虚拟机https://blog.csdn.net/zhenghuishengq/article/details/129544460【二】jvm的类加载子系统以及jclasslib的基本使用https://blog.csdn.net/zhenghuishengq/article/details/129610963【三】运行时私有区域之虚拟机栈…...

【GCU体验】基于PaddlePaddle + GCU跑通模型并测试GCU性能
一、环境 地址:启智社区:https://openi.pcl.ac.cn/ 二、计算卡介绍 云燧T20是基于邃思2.0芯片打造的面向数据中心的第二代人工智能训练加速卡,具有模型覆盖面广、性能强、软件生态开放等特点,可支持多种人工智能训练场景。同时具备灵活的可…...
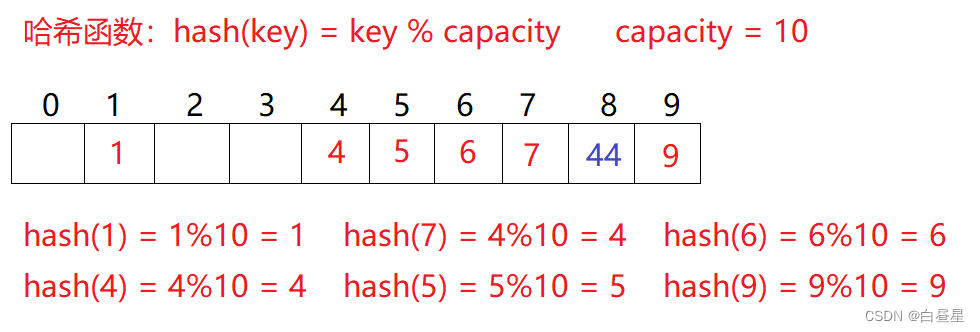
解析hash(散列)数据结构
前言 在学习完map、set这两个由红黑树构成的容器后,我们来到了这里hash,首先我们要有一个基础的认知——哈希和map与set的仅在使用时的差别区别:前者内部的元素没有序,而后者有序,其它的都相同,这里我们可…...

《2023金融科技·校园招聘白皮书》新鲜出炉|牛客独家
数智创新时代,科技人才为先。 眼下,在建设“数字中国”的时代背景下,金融行业全面数智化转型已箭在弦上。政策端,金融行业为中共中央、国务院印发《数字中国建设整体布局规划》的7大重点行业之一。 资本端,仅2022年三…...

文明的标志:书写系统、修建城市、使用金属器
文章目录 引言I 预备知识1.1 文明”和“文化”概念1.2 文明的标志1.3 应对水患II 定居开启了人类文明2.1 书写系统2.2 陶器2.3 家畜引言 一切和开启文明相关的技术都是围绕着两根主线展开: 多获取能量,以便于生存,信息能够管理起酋邦,总结、记录并传授经验。I 预备知识 1.…...

算法:将一个数组旋转k步
题目 输入一个数组如 [1,2,3,4,5,6,7],输出旋转 k 步后的数组。 旋转 1 步:就是把尾部的 7 放在数组头部前面,也就是 [7,1,2,3,4,5,6]旋转 2 步:就是把尾部的 6 放在数组头部前面,也就是 [6,7,1,2,3,4,5]… 思路 思…...

使用大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据
记录一下使用Java的SpringBoot大华SDK在智慧公厕项目中使大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据 首先根据说明书登录摄像头,一般摄像头都有自己的账号和密码(可能是admin admin 也可能是admin 888888 还有可能是admin 12345),…...

DC插装式流量阀压力阀
Cartridge Valves 电磁阀 止回阀 运动控制阀 流量控制阀 溢流阀 压力控制阀 顺序阀 梭阀 方向阀 配件 Zero Profile Valves 止回阀 运动控制阀 流量控制阀 溢流阀 梭阀 In-Line Valves 止回阀和梭阀 方向阀 配件 微型系列 AB20S APIDC-30S C10B C10S C10S…...

NumPy 数组学习手册:6~7
原文:Learning NumPy Array 协议:CC BY-NC-SA 4.0 译者:飞龙 六、性能分析,调试和测试 分析,调试和测试是开发过程的组成部分。 您可能熟悉单元测试的概念。 单元测试是程序员编写的用于测试其代码的自动测试。 例如&…...

【笔试强训选择题】Day6.习题(错题)解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、Day6习题(错题)解析 二、Day6习题(原题)练习 总结 前言 一、Day6习题(错题)解析…...

磁盘分区-LINUX
1、主分区(primary) 磁盘在Linux当中的命名: IDE /dev/hda hdb SCSI sda sdb 分区数字表示:sda1 、sda2、sda3 磁盘分区相当于给磁盘打隔断 ① 系统中必须要存在的分区,系统盘选择主分区安装 ② 数字编号只能是1-4&am…...
SpringAOP入门基础银行转账实例(进阶版)------------事务处理
SpringAOP入门基础银行转账实例**(进阶版)**------------事务处理 由上一节讲述的通过Connection和QueryRunner对事务进行的处理(详情可以去我之前写的博客文章:https://blog.csdn.net/m0_56245143/article/details/130069160?spm1001.2014…...

【python学习】基础篇-常用函数-format函数 格式化操作
format()可以对数据进行格式化处理操作,语法如下: format(value,format_spec) value 为要转换的数据,fommat spec 为格式化解释, 当参数 format spec 为空时,等同于函数 str(value)的方式。 format spec 可以设置非常复…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
