解析hash(散列)数据结构
前言
在学习完map、set这两个由红黑树构成的容器后,我们来到了这里hash,首先我们要有一个基础的认知——哈希和map与set的仅在使用时的差别区别:前者内部的元素没有序,而后者有序,其它的都相同,这里我们可以通过STL标准库对应的unordered_map和unordered_set的两个名字就能看出,那hash存在的意义在哪里?底层的数据结构又是如何实现的呢?
一、存在的意义(应用场景)
1.1 hash与红黑树(map、set)
在程序员的第一准则“绝不制造重复的轮子”下,明明有了map、set比hash(对应容器unordered_map和unordered_set)还能排序的容器,为啥我们还要添加它呢?我们使用时直接忽略有序不是一样用吗?
其实前人们也是这样想的,所以一开始是没有hash的对应标准容器的。


见上图,我们可以看到直到C++11标准unordered_map和unordered_set才推出。
1.2 hash的优势
其实hash推出的原因其实,我们可以类比List和Vector这两个容器,虽然这两容器的应用高度重叠,但是这两个容器由于本身的底层的结构不同在面对相同需求时,其效率相差甚远,所以这两个容器谁也替代不了对方。
hash的底层机构不像map、set的红黑树插入时需要排序旋转、但是由于其结构的特别又保留了查询的效率,所以相比红黑树的两个容器,hash的优势是大数据的查找。(为何有这些优势在下文结构介绍中)而红黑树的优势是自带排序和去重,还兼顾了查找效率。
二、底层结构
2.1 哈希概念
注:
- 关键码(key)可以理解为可以代表元素成员变量的唯一代表值,就如我们的身份证号一样。
- 哈希函数:将元素转化为关键码的方法。
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素
时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即
O(log_2 N),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。
如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立
一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称
为哈希表(Hash Table)(或者称散列表)。
举个生活的栗子:大家使用字典时,会根据字的拼音字母依次翻到对应页数,而每个字母在字典上的映射页数都是已知可查的,直接跳到对应页数即可。(在下文的进一步解析中,我们将以vector来作为“字典”)。
当向该结构中
- 插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放
- 搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置
取元素比较,若关键码相等,则搜索成功。
例如:数据集合{1,7,6,4,5,9};
哈希函数设置为:hash(key) = key % capacity; capacity(哈希函数:将元素转化为关键码的方法)为存储元素底层空间总的大小。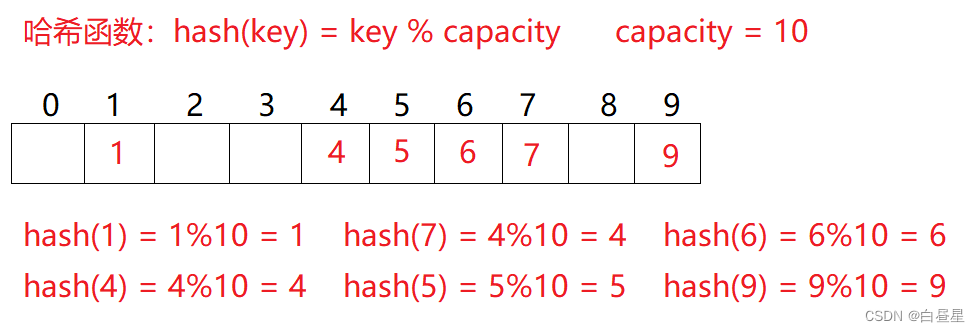
用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快。
问题:按照上述哈希方式,向集合中插入元素44,会出现什么问题?(答案在下个标题)
2.2 哈希冲突与哈希函数
①哈希冲突
对于两个数据元素的关键字k_i和 k_j,有k_i != k_j,但有:Hash(k_i) == Hash(k_j),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
发生哈希冲突该如何处理呢?
②哈希函数
引起哈希冲突的一个重要原因可能是:哈希函数设计不够合理。
哈希函数设计原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m(capacity)个地址时,其值域必须在0到m-1之间。
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单(哈希函数需要被对应容器频繁调用,不能因为它将hash的效率降下去)
string的哈希函数的算法![]() https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html
https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html
常见哈希函数
1. 直接定址法--(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B
优点:简单、均匀
缺点:需要事先知道关键字的分布情况
使用场景:适合查找比较小且连续的情况
2. 除留余数法--(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,
按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址。(上面的例子就是)
3. 平方取中法
假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址;
再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况
4.数学分析法
利用不同的元素的概率分布情况,制定出对应的哈希函数。
例如:设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定
相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只
有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散
列地址。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的
若干位分布较均匀的情况
注意:
- 哈希函数设计的越精妙,产生哈希冲突的可能性就越低
- 由于不同的哈希函数对于关键码的生成方式不同,带来的冲突结果也不同
- 哈希冲突在理论上是不可避免的,举几个栗子:
1、我们将10个成员放入到capacity只有9的哈希表中,至少有一个会冲突。
2、由于数据分布集中而hash函数实现没有将集中的元素分开,就会导致冲突加重。
既然哈希函数无法从根本的解决哈希冲突,那遇到它时该如何解决呢?
2.3 哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列(哈希桶)。
①结构:闭散列
也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有
空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置
呢?
②结构:开散列/哈希桶(常用)
1. 开散列概念
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地
址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链
接起来,各链表的头结点存储在哈希表中。
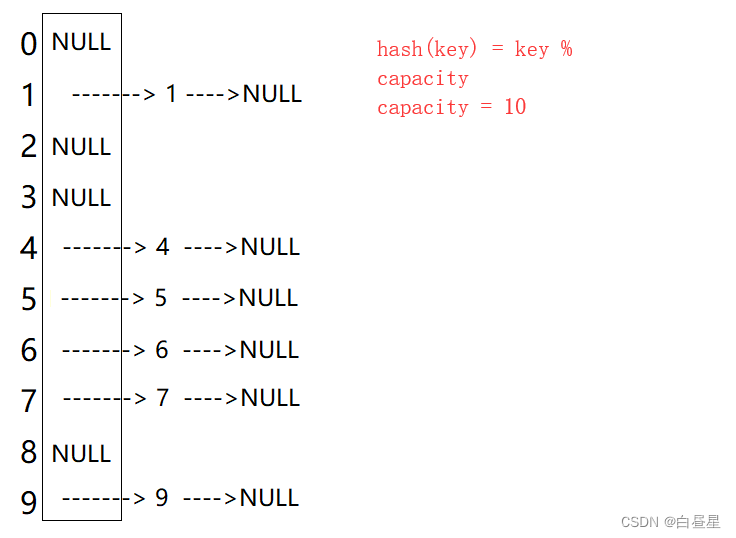
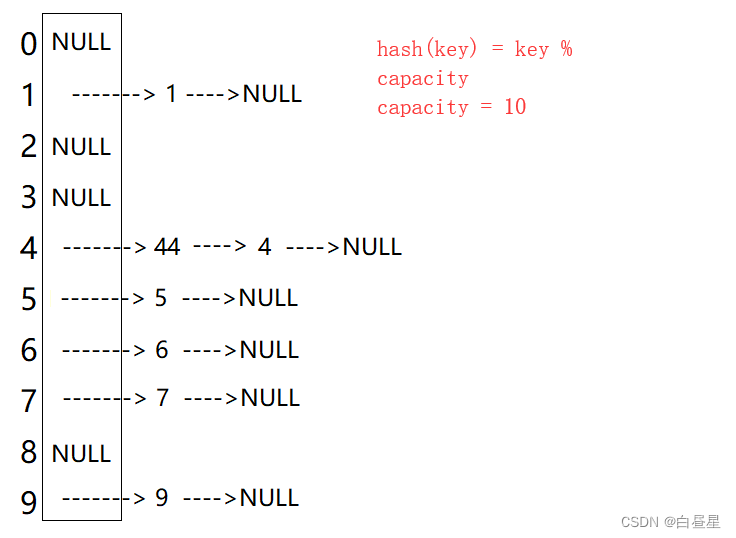
从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
template<class V>
struct HashBucketNode
{HashBucketNode(const V& data): _pNext(nullptr), _data(data){}HashBucketNode<V>* _pNext;V _data;
};
// 本文所实现的哈希桶中key是唯一的
template<class V>
class HashBucket
{typedef HashBucketNode<V> Node;typedef Node* PNode;
public:HashBucket(size_t capacity = 3) : _size(0){_ht.resize(GetNextPrime(capacity), nullptr);}// 哈希桶中的元素不能重复PNode* Insert(const V& data){// 确认是否需要扩容。。。// _CheckCapacity();// 1. 计算元素所在的桶号size_t bucketNo = HashFunc(data);// 2. 检测该元素是否在桶中PNode pCur = _ht[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}// 3. 插入新元素pCur = new Node(data);pCur->_pNext = _ht[bucketNo];_ht[bucketNo] = pCur;_size++;return pCur;}// 删除哈希桶中为data的元素(data不会重复),返回删除元素的下一个节点PNode* Erase(const V& data){size_t bucketNo = HashFunc(data);PNode pCur = _ht[bucketNo];PNode pPrev = nullptr, pRet = nullptr;while (pCur){if (pCur->_data == data){if (pCur == _ht[bucketNo])_ht[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;pRet = pCur->_pNext;delete pCur;_size--;return pRet;}}return nullptr;}PNode* Find(const V& data);size_t Size()const;bool Empty()const;void Clear();bool BucketCount()const;void Swap(HashBucket<V, HF>& ht;~HashBucket();
private:size_t HashFunc(const V& data){return data % _ht.capacity();}
private:vector<PNode*> _ht;size_t _size; // 哈希表中有效元素的个数
};③开散列增容
桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可
能会导致一个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希
表进行增容,那该条件怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点,
再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可
以给哈希表增容。
void _CheckCapacity()
{size_t bucketCount = BucketCount();if (_size == bucketCount){HashBucket<V, HF> newHt(bucketCount);for (size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx){PNode pCur = _ht[bucketIdx];while (pCur){// 将该节点从原哈希表中拆出来_ht[bucketIdx] = pCur->_pNext;// 将该节点插入到新哈希表中size_t bucketNo = newHt.HashFunc(pCur->_data);pCur->_pNext = newHt._ht[bucketNo];newHt._ht[bucketNo] = pCur;pCur = _ht[bucketIdx];}}newHt._size = _size;this->Swap(newHt);}
}④ 开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销。事实上:由于开地址法必须保持大量的空闲空间以确保搜索效率,如二次探查法要求装载因子a <=0.7(见下文),而表项所占空间又比指针大的多,所以使用链地址法反而比开地址法节省存储空间
1. 探测方式:线性探测
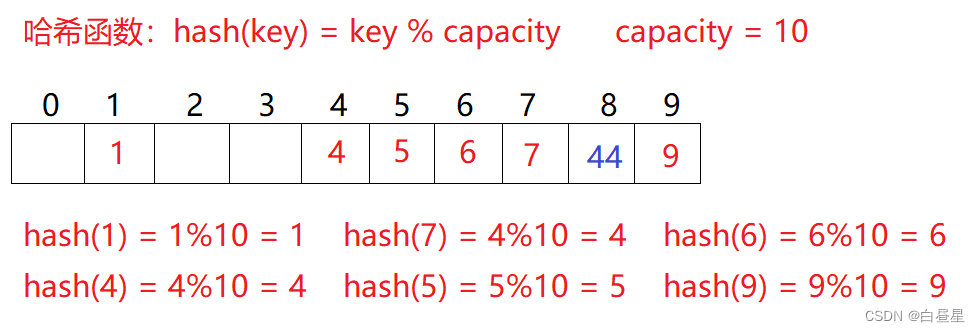
比如2.1中的场景,现在需要插入元素44,先通过哈希函数计算哈希地址,hashAddr为4,
因此44理论上应该插在该位置,但是该位置已经放了值为4的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
-
插入
通过哈希函数获取待插入元素在哈希表中的位置
如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,
使用线性探测找到下一个空位置,插入新元素
- 删除
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素
会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影
响。因此线性探测采用标记的伪删除法来删除一个元素。
线性探测 + 闭散列的实现:
// 哈希表每个空间给个标记
// EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除
enum State
{EMPTY, EXIST, DELETE
};// 注意:假如实现的哈希表中元素唯一,即key相同的元素不再进行插入
// 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起
template<class K, class V>
class HashTable
{struct Elem{pair<K, V> _val;State _state;};
public:HashTable(size_t capacity = 3): _ht(capacity), _size(0){for (size_t i = 0; i < capacity; ++i)_ht[i]._state = EMPTY;}bool Insert(const pair<K, V>& val){// 检测哈希表底层空间是否充足// _CheckCapacity();size_t hashAddr = HashFunc(key);// size_t startAddr = hashAddr;while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first== key)return false;hashAddr++;if (hashAddr == _ht.capacity())hashAddr = 0;/*// 转一圈也没有找到,注意:动态哈希表,该种情况可以不用考虑,哈希表中元素个数到达一定的数量,哈希冲突概率会增大,需要扩容来降低哈希冲突,因此哈希表中元素是不会存满的if(hashAddr == startAddr)return false;*/}// 插入元素_ht[hashAddr]._state = EXIST;_ht[hashAddr]._val = val;_size++;return true;}int Find(const K& key){size_t hashAddr = HashFunc(key);while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first== key)return hashAddr;hashAddr++;}return hashAddr;}bool Erase(const K& key){int index = Find(key);if (-1 != index){_ht[index]._state = DELETE;_size++;return true;}return false;}size_t Size()const;bool Empty() const;void Swap(HashTable<K, V, HF>& ht);
private:size_t HashFunc(const K& key){return key % _ht.capacity();}
private:vector<Elem> _ht;size_t _size;
};线性探测优点:实现非常简单,
线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同
关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降
低。如何缓解呢?
2.探测方式: 二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位
置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为(平方数):H_i = (H_0 + i^2 )% m, 或者:H_i = (H_0 - i^2 )% m。其中:i =1,2,3…, H_0是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置,m是表的大小。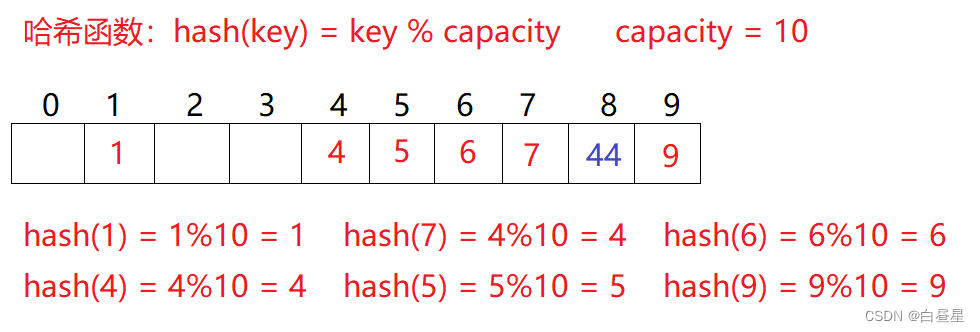
小结:哈希(unordered_map、unordered_set)作为以“映射”的方式储存内容,具备了高效的搜索和较低存储代价的特点,和强大的红黑树对应的set、map容器做到了再次补充。
我的博客即将同步至腾讯云+社区,邀请大家一同入驻:https://cloud.tencent.com/developer/support-plan?invite_code=1omyl741mq270
相关文章:

解析hash(散列)数据结构
前言 在学习完map、set这两个由红黑树构成的容器后,我们来到了这里hash,首先我们要有一个基础的认知——哈希和map与set的仅在使用时的差别区别:前者内部的元素没有序,而后者有序,其它的都相同,这里我们可…...

《2023金融科技·校园招聘白皮书》新鲜出炉|牛客独家
数智创新时代,科技人才为先。 眼下,在建设“数字中国”的时代背景下,金融行业全面数智化转型已箭在弦上。政策端,金融行业为中共中央、国务院印发《数字中国建设整体布局规划》的7大重点行业之一。 资本端,仅2022年三…...

文明的标志:书写系统、修建城市、使用金属器
文章目录 引言I 预备知识1.1 文明”和“文化”概念1.2 文明的标志1.3 应对水患II 定居开启了人类文明2.1 书写系统2.2 陶器2.3 家畜引言 一切和开启文明相关的技术都是围绕着两根主线展开: 多获取能量,以便于生存,信息能够管理起酋邦,总结、记录并传授经验。I 预备知识 1.…...

算法:将一个数组旋转k步
题目 输入一个数组如 [1,2,3,4,5,6,7],输出旋转 k 步后的数组。 旋转 1 步:就是把尾部的 7 放在数组头部前面,也就是 [7,1,2,3,4,5,6]旋转 2 步:就是把尾部的 6 放在数组头部前面,也就是 [6,7,1,2,3,4,5]… 思路 思…...

使用大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据
记录一下使用Java的SpringBoot大华SDK在智慧公厕项目中使大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据 首先根据说明书登录摄像头,一般摄像头都有自己的账号和密码(可能是admin admin 也可能是admin 888888 还有可能是admin 12345),…...

DC插装式流量阀压力阀
Cartridge Valves 电磁阀 止回阀 运动控制阀 流量控制阀 溢流阀 压力控制阀 顺序阀 梭阀 方向阀 配件 Zero Profile Valves 止回阀 运动控制阀 流量控制阀 溢流阀 梭阀 In-Line Valves 止回阀和梭阀 方向阀 配件 微型系列 AB20S APIDC-30S C10B C10S C10S…...

NumPy 数组学习手册:6~7
原文:Learning NumPy Array 协议:CC BY-NC-SA 4.0 译者:飞龙 六、性能分析,调试和测试 分析,调试和测试是开发过程的组成部分。 您可能熟悉单元测试的概念。 单元测试是程序员编写的用于测试其代码的自动测试。 例如&…...

【笔试强训选择题】Day6.习题(错题)解析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、Day6习题(错题)解析 二、Day6习题(原题)练习 总结 前言 一、Day6习题(错题)解析…...

磁盘分区-LINUX
1、主分区(primary) 磁盘在Linux当中的命名: IDE /dev/hda hdb SCSI sda sdb 分区数字表示:sda1 、sda2、sda3 磁盘分区相当于给磁盘打隔断 ① 系统中必须要存在的分区,系统盘选择主分区安装 ② 数字编号只能是1-4&am…...
SpringAOP入门基础银行转账实例(进阶版)------------事务处理
SpringAOP入门基础银行转账实例**(进阶版)**------------事务处理 由上一节讲述的通过Connection和QueryRunner对事务进行的处理(详情可以去我之前写的博客文章:https://blog.csdn.net/m0_56245143/article/details/130069160?spm1001.2014…...

【python学习】基础篇-常用函数-format函数 格式化操作
format()可以对数据进行格式化处理操作,语法如下: format(value,format_spec) value 为要转换的数据,fommat spec 为格式化解释, 当参数 format spec 为空时,等同于函数 str(value)的方式。 format spec 可以设置非常复…...

团团面试经验
1、Redis同时访问大量不存在的key会发生什么? 如果是缓存和数据库中都不存在,那么就会发生缓存穿透。 举个例子:某个黑客故意制造一些非法的 key 发起大量请求,导致大量请求落到数据库,结果数据库上也没有查到对应的数…...

今天面了个京东拿 38K 出来的,让我见识到了基础的天花板
今年的春招已经开始了,很多小伙伴收获不错,拿到了心仪的 offer。 各大论坛和社区里也看见不少小伙伴慷慨地分享了常见的软件测试面试题和八股文,为此咱这里也统一做一次大整理和大归类,这也算是划重点了。 俗话说得好࿰…...
Qt创建SDK库(dll动态库)并调用SDK库(dll动态库)
Qt创建SDK库(dll动态库)并调用SDK库(dll动态库) 一、项目场景 在日常的项目中,我们经常会遇到调用别人的数学库、线程库、图形库等操作。这些库通常就被称为SDK,SDK全称是Software Development Kit(软件开发工具包),…...

400以内的蓝牙耳机哪款好?400以内蓝牙耳机排行榜
谈起TWS,无论是传统的音频厂商还是手机厂商,都是其不可或缺的重要产品线,现在很多许多蓝牙耳机都不是千篇一律得形状,市场也鲜有商家在外观上下功夫,下面分享几款400元以内,内外兼具的耳机品牌。 一、南卡…...
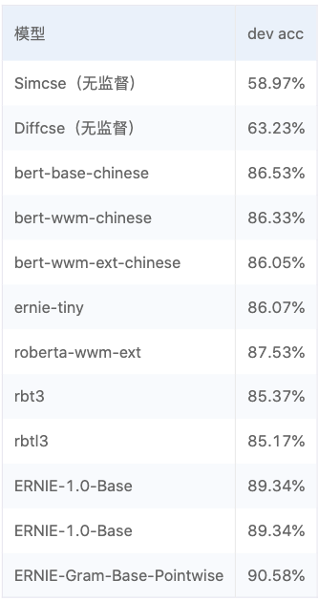
基于飞桨实现的特定领域知识图谱融合方案:ERNIE-Gram文本匹配算法
文本匹配任务在自然语言处理领域中是非常重要的基础任务,一般用于研究两段文本之间的关系。文本匹配任务存在很多应用场景,如信息检索、问答系统、智能对话、文本鉴别、智能推荐、文本数据去重、文本相似度计算、自然语言推理、问答系统、信息检索等&…...
前端基础复习
1.什么叫HTML5?和原本的所说的HTML有什么区别? 本质上html和html5是一样的的。区别有: 1. 在文档类型声明上 HTML4.0 <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loos…...

Vue2 API-源码解析
目录 Vue.extend(option) delimiters functional Vue.component(id, Function | Object) Vue.directive( id, [definition] ) Vue.filter( id, function) Vue.nextTick() Vue.set() Vue.delete(target, index/key) Vue.compile(template) Vue.observable(object) …...
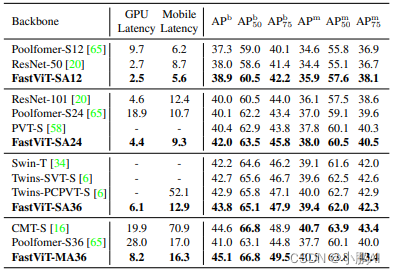
FastViT: A Fast Hybrid Vision Transformer using Structural Reparameterization
FastViT: A Fast Hybrid Vision Transformer using Structural Reparameterization 论文地址:https://arxiv.org/pdf/2303.14189.pdf 概述 本文提出了一种通用的 CNN 和 Transformer 混合的视觉基础模型 移动设备和 ImageNet 数据集上的精度相同的前提下…...

C/C++文档阅读笔记-A Simple Makefile Tutorial解析
Makefile文件可以使得程序编译变得简单。本博文并不是很系统的讲解makefile,本博文的目标是让读者快速编写自己的makefile文件并能应用到中小项目中。 简单实例 举个例子有下面3个文件,分别是hellomake.c,hellofunc.c,hellomake.…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
