磁盘分区-LINUX
1、主分区(primary)
磁盘在Linux当中的命名:
IDE /dev/hda hdb
SCSI sda sdb
分区数字表示:sda1 、sda2、sda3
磁盘分区相当于给磁盘打隔断
① 系统中必须要存在的分区,系统盘选择主分区安装
② 数字编号只能是1-4(sda1、sda2、sda3、sda4)
③ 主分区最多四个,最少一个
2、扩展分区(extend)
① 相当于一个独立的小磁盘。独立的分区表,不能独立存在。
② 有独立的分区表
③ 不能独立存在,即不能独立的存放数据。
④ 必须在扩展分区上建立逻辑分区才能存放数据。
⑤ 占用主分区的编号(主分区+扩展分区)之和最多4个
3、逻辑分区(logic)
① 数字编号只能从5号开始
②存放于扩展分区之上
③存放任意普通数据
注意:磁盘分区注意事要点
一块硬盘的分区方式只能为如下组合之一:
1、任意多个主分区,但只要求主分区数量大于等于1,小于等于4;
例如:一个硬盘可以分为4个主分区、3个主分区、2个主分区或者1个主分区
2、扩展分区可以和主分区组合,但要求主分区+扩展分区的数量大于等于2和小于等于4;
3、一个盘如果分区分完了,但是还有剩余的空间,则剩余的空间就浪费掉
相关文章:

磁盘分区-LINUX
1、主分区(primary) 磁盘在Linux当中的命名: IDE /dev/hda hdb SCSI sda sdb 分区数字表示:sda1 、sda2、sda3 磁盘分区相当于给磁盘打隔断 ① 系统中必须要存在的分区,系统盘选择主分区安装 ② 数字编号只能是1-4&am…...
SpringAOP入门基础银行转账实例(进阶版)------------事务处理
SpringAOP入门基础银行转账实例**(进阶版)**------------事务处理 由上一节讲述的通过Connection和QueryRunner对事务进行的处理(详情可以去我之前写的博客文章:https://blog.csdn.net/m0_56245143/article/details/130069160?spm1001.2014…...

【python学习】基础篇-常用函数-format函数 格式化操作
format()可以对数据进行格式化处理操作,语法如下: format(value,format_spec) value 为要转换的数据,fommat spec 为格式化解释, 当参数 format spec 为空时,等同于函数 str(value)的方式。 format spec 可以设置非常复…...

团团面试经验
1、Redis同时访问大量不存在的key会发生什么? 如果是缓存和数据库中都不存在,那么就会发生缓存穿透。 举个例子:某个黑客故意制造一些非法的 key 发起大量请求,导致大量请求落到数据库,结果数据库上也没有查到对应的数…...

今天面了个京东拿 38K 出来的,让我见识到了基础的天花板
今年的春招已经开始了,很多小伙伴收获不错,拿到了心仪的 offer。 各大论坛和社区里也看见不少小伙伴慷慨地分享了常见的软件测试面试题和八股文,为此咱这里也统一做一次大整理和大归类,这也算是划重点了。 俗话说得好࿰…...
Qt创建SDK库(dll动态库)并调用SDK库(dll动态库)
Qt创建SDK库(dll动态库)并调用SDK库(dll动态库) 一、项目场景 在日常的项目中,我们经常会遇到调用别人的数学库、线程库、图形库等操作。这些库通常就被称为SDK,SDK全称是Software Development Kit(软件开发工具包),…...

400以内的蓝牙耳机哪款好?400以内蓝牙耳机排行榜
谈起TWS,无论是传统的音频厂商还是手机厂商,都是其不可或缺的重要产品线,现在很多许多蓝牙耳机都不是千篇一律得形状,市场也鲜有商家在外观上下功夫,下面分享几款400元以内,内外兼具的耳机品牌。 一、南卡…...
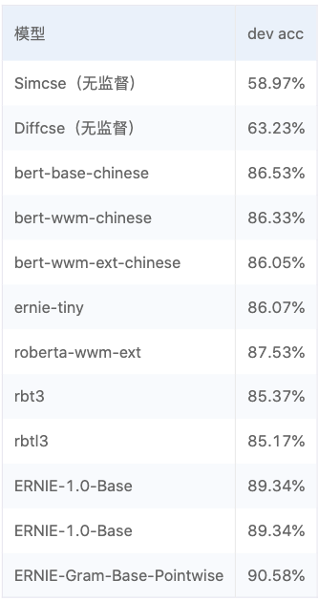
基于飞桨实现的特定领域知识图谱融合方案:ERNIE-Gram文本匹配算法
文本匹配任务在自然语言处理领域中是非常重要的基础任务,一般用于研究两段文本之间的关系。文本匹配任务存在很多应用场景,如信息检索、问答系统、智能对话、文本鉴别、智能推荐、文本数据去重、文本相似度计算、自然语言推理、问答系统、信息检索等&…...
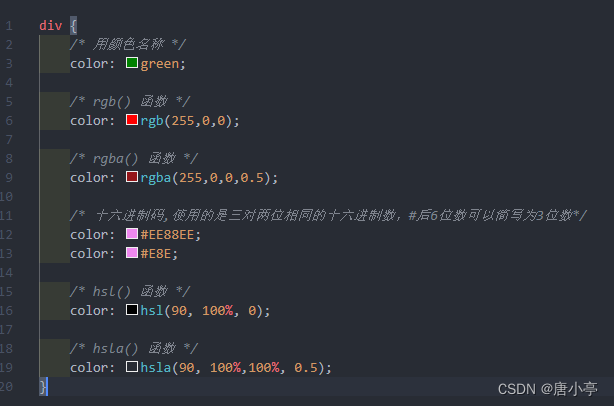
前端基础复习
1.什么叫HTML5?和原本的所说的HTML有什么区别? 本质上html和html5是一样的的。区别有: 1. 在文档类型声明上 HTML4.0 <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loos…...

Vue2 API-源码解析
目录 Vue.extend(option) delimiters functional Vue.component(id, Function | Object) Vue.directive( id, [definition] ) Vue.filter( id, function) Vue.nextTick() Vue.set() Vue.delete(target, index/key) Vue.compile(template) Vue.observable(object) …...
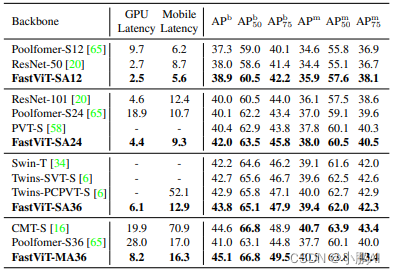
FastViT: A Fast Hybrid Vision Transformer using Structural Reparameterization
FastViT: A Fast Hybrid Vision Transformer using Structural Reparameterization 论文地址:https://arxiv.org/pdf/2303.14189.pdf 概述 本文提出了一种通用的 CNN 和 Transformer 混合的视觉基础模型 移动设备和 ImageNet 数据集上的精度相同的前提下…...

C/C++文档阅读笔记-A Simple Makefile Tutorial解析
Makefile文件可以使得程序编译变得简单。本博文并不是很系统的讲解makefile,本博文的目标是让读者快速编写自己的makefile文件并能应用到中小项目中。 简单实例 举个例子有下面3个文件,分别是hellomake.c,hellofunc.c,hellomake.…...

GraphSAGE的基础理论
文章目录GraphSAGE原理(理解用)GraphSAGE工作流程GraphSAGE的实用基础理论(编代码用)1. GraphSAGE的底层实现(pytorch)PyG中NeighorSampler实现节点维度的mini-batch GraphSAGE样例PyG中的SAGEConv实现2. …...

Windows 安装 GDAL C++库
Windows 安装 GDAL C库1. 方法1:下载配置网友编译的GDAL版本1.1 下载1.2 配置1.3 测试1.4 缺点2. 方法2:自己编译3. 参考1. 方法1:下载配置网友编译的GDAL版本 1.1 下载 CSDN: GDAL,geos联合编译的库,版本为1.8.0&am…...

二叉树基础概念
1.二叉树种类 1.1 满二叉树 满二叉树:如果一棵二叉树只有度为 0 0 0 的结点和度为 2 2 2 的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。 如图所示: 这棵二叉树为满二叉树,也可以说深度为 k k k&…...

【MySQL】(1)数据库基础,库与表的增删查改,数据库的备份与还原
文章目录服务器,数据库,表关系MySQL 数据存储逻辑SQL 分类存储引擎库的操作查看数据库创建数据库查看创建语句删除数据库选择(切换)数据库查看当前选择的数据库修改数据库字符集和排序规则表的操作创建表查询表查询表结构插入数据…...

Python基础-01 变量
注释 注释的分类 在Python中,支持单行及多行注释 单行注释 使用#对代码进行说明,#右边的所有内容就是注释的内容,起辅助说明作用 # #右边的都是注释,解析器会忽略 print(hello world) #在控制台里打印一段话多行注释 多行注释中,允许换行,使用三个单引号开始,三个单引号结…...
springcloud2.1.0整合seata1.5.2+nacos2.10(附源码)
springcloud2.1.0整合seata1.5.2nacos2.10(附源码) 1.创建springboot2.2.2springcloud2.1.0的maven父子工程如下,不过多描述: 搭建过程中也出现很多问题,主要包括: 1.seataServer.properties配置文件的组…...

map原理
map源码结构体: type hmap struct {count int // 元素的个数B uint8 // buckets 数组的长度就是 2^B 个overflow uint16 // 溢出桶的数量buckets unsafe.Pointer // 2^B个桶对应的数组指针oldbuckets unsafe.Pointer // 发生扩容时࿰…...
概览)
[Ext JS]3.6 Ext JS 表格(Grid)概览
Grid, 翻译过来是网格, 也就是表格。 Grid 的基本构成 面板 :Ext.grid.Panel表格视图 :Ext.view.Table。 不直接使用, 通过面板的viewConfig配置项进行配置。比如可以用来配置表格中行是否跳色显示列: Ext.grid.column.Column。 表格中的列定义store , 表格的数据示例代码…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...
