《算法竞赛进阶指南》0x51 线性DP
0x51 线性DP
271. 杨老师的照相排列
题意:
NNN 个人站成左端对齐的 kkk 排,每排有 NiN_iNi 人,Ni>NjN_i > N_jNi>Nj 如果 i<ji < ji<j,则 Ni>NjN_i > N_jNi>Nj 。每一排从左到右身高递减,每一列从后到前身高递减。询问方案数。
解析:
按照身高从大到小的顺序决定位置。在任意时刻,已经确定位置的人在每一行中一定是从左开始的连续位置。
用 kkk 元组可以描述当前已经确定的位置。在决定当前人的位置时,可放的排为没放满的排,且放完后满足 ni>nj(i<j)n_i > n_j (i < j)ni>nj(i<j),nin_ini 为第 iii 排已经放的人数。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 32;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int n[6];
int k;
ll dp[maxn][maxn][maxn][maxn][maxn];
int check(int a, int b, int c, int d, int e){return a >= b && b >= c && c >= d && d >= e && e >= 0;
}
void solve(){memset(dp, 0, sizeof(dp));dp[0][0][0][0][0] = 1;for(int a = 0; a <= n[1]; a++){for(int b = 0; b <= n[2]; b++){for(int c = 0; c <= n[3]; c++){for(int d = 0; d <= n[4]; d++){for(int e = 0; e <= n[5]; e++){if(!check(a, b, c, d, e))continue;if(check(a-1, b, c, d, e))dp[a][b][c][d][e] += dp[a-1][b][c][d][e];if(check(a, b-1, c, d, e))dp[a][b][c][d][e] += dp[a][b-1][c][d][e];if(check(a, b, c-1, d, e))dp[a][b][c][d][e] += dp[a][b][c-1][d][e];if(check(a, b, c, d-1, e))dp[a][b][c][d][e] += dp[a][b][c][d-1][e];if(check(a, b, c, d, e-1))dp[a][b][c][d][e] += dp[a][b][c][d][e-1];}}}}}//cout << "ans = ";cout << dp[n[1]][n[2]][n[3]][n[4]][n[5]] << endl;
}
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);while(1){cin >> k;if(k == 0)break;memset(n, 0, sizeof(n));for(int i = 1; i <= k; i++)cin >> n[i];solve();}return 0;
}最长公共上升子序列
题意:
给定两个序列 a,ba, ba,b,询问最长公共上升子序列的长度
解析:
令 fi,jf_{i,j}fi,j 为在 aaa 的前 iii 个数和 bbb 的前 jjj 个数中以 bjb_jbj 的最长公共上升子序列的长度。
- 不选 aia_iai,fi,j=fi−1,jf_{i,j} = f_{i-1, j}fi,j=fi−1,j
- 选了 aia_iai,fi,j=maxbk<bj{fi−1,k+1}f_{i,j} = \max\limits_{b_k<b_j}\{f_{i-1,k}+1\}fi,j=bk<bjmax{fi−1,k+1}
此时时间复杂度为 O(n3)O(n^3)O(n3)。
容易发现每次都是从 ai>bka_i > b_kai>bk 的前缀最大值转移过来,增加一个变量记录 fi−1,kf_{i-1,k}fi−1,k 的前缀最大值。此时时间复杂度为 O(n2)O(n^2)O(n2)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 3e3+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int n, a[maxn], b[maxn];
int f[maxn][maxn], ans;
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];for(int i = 1; i <= n; i++)cin >> b[i];for(int i = 1; i <= n; i++){int maxx = 0;for(int j = 1; j <= n; j++){f[i][j] = f[i-1][j];if(a[i] == b[j])f[i][j] = max(f[i][j], maxx+1);else if(a[i] > b[j])maxx = max(maxx, f[i][j]);if(i == n)ans = max(ans, f[i][j]);}}cout << ans << endl;return 0;
}
分级
题意:
给定序列 AAA,构造非严格的单调序列 BBB,使 S=∑i=1n∣Ai−Bi∣S = \sum\limits_{i=1}\limits^n |A_i-B_i|S=i=1∑n∣Ai−Bi∣ 最小。询问最小值。
解析
结论: 一定存在一组最优解,使得每个 BiB_iBi 都存在 jjj,满足 Bi=AjB_i = A_jBi=Aj
令 fi,jf_{i,j}fi,j 为确定前 iii 数,且第 iii 个数为 CjC_jCj ,CCC 为升序排序后的 AAA 序列。
fi,j=mink<=j{fi−1,k+∣Cj−Ai∣}f_{i,j} = \min\limits_{k <= j}\{ f_{i-1,k} + |C_j-A_i|\}fi,j=k<=jmin{fi−1,k+∣Cj−Ai∣}维护前缀最小值,可在 O(1)O(1)O(1) 时间转移
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 2e3+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int n, a[maxn], c[maxn];
int ans = INF;
bool cmp(int a, int b){return a > b;
}
int f[maxn][maxn];
void solve(){memset(f, 0, sizeof(f));int res = INF; for(int i = 1; i <= n; i++){int minn = INF;for(int j = 1; j <= n; j++){minn = min(minn, f[i-1][j]);f[i][j] = minn + abs(a[i]-c[j]);}}for(int i = 1; i <= n; i++)res = min(res, f[n][i]);ans = min(ans, res);
}
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];c[i] = a[i];}sort(c+1, c+1+n);solve();sort(c+1, c+1+n, cmp);solve();cout << ans << endl;return 0;
}移动服务
题意:
有 3 个人。有 nnn 个请求一个人去某地,移动有代价。依次满足请求,询问最小代价。
题意:
令 fi,x,yf_{i, x, y}fi,x,y 表示满足前 iii 个请求后,三人位于 posi,x,ypos_i, x, yposi,x,y 时的最小代价。
每个状态可以转移到另外三个状态,见代码。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
const int maxn = 1e3+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int L, n;
int p[maxn], c[210][210];
int dp[maxn][210][210];
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> L >> n; for(int i = 1; i <= L; i++)for(int j = 1; j <= L; j++)cin >> c[i][j];for(int i = 1; i <= n; i++)cin >> p[i];memset(dp, INF, sizeof(dp));dp[0][1][2] = 0; p[0] = 3;for(int i = 0; i < n; i++){for(int x = 1; x <= L; x++){for(int y = 1; y <= L; y++){if(x == y || y == p[i] || x == p[i])continue;int u = p[i+1];dp[i+1][x][y] = min(dp[i+1][x][y], dp[i][x][y] + c[p[i]][u]);dp[i+1][x][p[i]] = min(dp[i+1][x][p[i]], dp[i][x][y] + c[y][u]);dp[i+1][p[i]][y] = min(dp[i+1][p[i]][y], dp[i][x][y] + c[x][u]);}}}int res = INF;for(int i = 1; i <= L; i++)for(int j = 1; j <= L; j++)res = min(res, dp[n][i][j]);cout << res << endl;return 0;
}传纸条
题意:
m×nm\times nm×n 的矩阵,每次可以向右或者向下走一步。从左上角都右下角选择两条互不相交(在路径端点可以相交)的路径,使点权和最大。
解析:
令 fi,j,x,yf_{i,j,x,y}fi,j,x,y 为第一条路径走到 (i,j)(i,j)(i,j) 且第二条路径走到 (x,y)(x,y)(x,y) 的最大点权和
对于 (i,j)=(x,y)(i,j) = (x,y)(i,j)=(x,y) 的状态,只计算一次点权
也可以网络流。
把每个点拆成入点和出点,入点向出点连边,容量1,费用为点权。
每个点的出点向能到达的点的入点连边,容量INF,费用 0;再连一条边,容量INF,费用 0.
源点向起点的入点连边,容量2,费用 0;终点的出点向汇点连边,容量2,费用 0 。
参考洛谷上 Duan2baka 大佬题解
代码:
#include<iostream>
#include<algorithm>
using namespace std;
int dp[55][55][55][55],a[55][55],n,m;
int main(){cin >> m >> n;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++)cin >> a[i][j];}for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)for (int k = 1; k <= m; k++)for (int l = 1; l <= n; l++) {dp[i][j][k][l]=max(max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1]),max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1]))+a[i][j]+a[k][l];if(i==k && j==l) dp[i][j][k][l] -= a[i][j];}cout << dp[m][n][m][n];
}
饼干
题意:
mmm 个饼干,分给 nnn 个人。每个人有参数 gig_igi,如果有 aia_iai 个人的饼干多于 iii ,则 iii 产生 ai×gia_i \times g_iai×gi 的怨气。
每个孩子最少分一个饼干,询问最少的怨气。
解析:
贪心的考虑,ggg 大的人一定分的多于 ggg 少的人。否则可以交换,结果不会变劣。
令 fi,jf_{i,j}fi,j 为前 iii 个孩子分了 jjj 个饼干的最小怨气和。
如果当前第 iii 个人的饼干数大于 1,则前 iii 个人饼干数都大于 1。每个人都减去一个饼干,aaa 不变,所以 fi,j=fi,j−if_{i,j} = f_{i,j-i}fi,j=fi,j−i 。
如果当前第 iii 个人的饼干数为1,枚举有多少人饼干数不为 1
fi,j=min0≤k<i{fk,j−i+k+k∑t=k+1igt}f_{i,j} = \min\limits_{0\le k<i}\{f_{k,j-i+k}+k\sum\limits_{t = k+1}\limits^ig_t\}fi,j=0≤k<imin{fk,j−i+k+kt=k+1∑igt}
时间复杂度为 O(n3m)O(n^3m)O(n3m)。也可以前缀和优化一下,时间复杂度变成 O(n2m)O(n^2m)O(n2m)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
#define mkp(a, b) make_pair((a), (b))
const int maxn = 3e2+10;
const int maxm = 5e3+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;struct node{int g, id;node(){}node(int g, int id) : g(g), id(id){}bool operator < (const node &b) const{return g > b.g;}
}s[maxn];
int g[maxn], sum[maxn];
int f[maxn][maxm];
pii fr[maxn][maxm];
int res[maxn];
void cal(int x, int y){if(x == 0)return;cal(fr[x][y].first, fr[x][y].second);if(fr[x][y].first == x){for(int i = 1; i <= x; i++)res[s[i].id]++;}else{for(int i = fr[x][y].first+1; i <= x; i++)res[s[i].id] = 1;}
}
int n, m;
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= n; i++){cin >> s[i].g;s[i].id = i;} sort(s+1, s+1+n);for(int i = 1; i <= n; i++)sum[i] = sum[i-1] + s[i].g;memset(f, INF, sizeof(f));f[0][0] = 0;for(int i = 1; i <= n; i++){for(int j = i; j <= m; j++){f[i][j] = f[i][j-i];fr[i][j] = mkp(i, j-i);for(int k = 0; k < i; k++){if(f[i][j] > f[k][j-i+k] + k*(sum[i]-sum[k])){f[i][j] = f[k][j-i+k] + k*(sum[i]-sum[k]);fr[i][j] = mkp(k, j-i+k);}}}}cout << f[n][m] << endl;cal(n, m);for(int i = 1; i <= n; i++)cout << res[i] << " ";cout << endl;return 0;
}
相关文章:

《算法竞赛进阶指南》0x51 线性DP
0x51 线性DP 271. 杨老师的照相排列 题意: NNN 个人站成左端对齐的 kkk 排,每排有 NiN_iNi 人,Ni>NjN_i > N_jNi>Nj 如果 i<ji < ji<j,则 Ni>NjN_i > N_jNi>Nj 。每一排从左到右身高递减&…...

spring数据库事务管理
1.什么是事务 事务是逻辑上的一组操作,要么都执行,要么都不执行。 需要注意的是:事务能否生效数据库引擎是否支持事务是关键。比如常用的 MySQL 数据库默认使用支持事务的 innodb引擎。但是,如果把数据库引擎变为 myisam&#x…...

Huggingface微调BART的代码示例:WMT16数据集训练新的标记进行翻译
BART模型是用来预训练seq-to-seq模型的降噪自动编码器(autoencoder)。它是一个序列到序列的模型,具有对损坏文本的双向编码器和一个从左到右的自回归解码器,所以它可以完美的执行翻译任务。 如果你想在翻译任务上测试一个新的体系…...
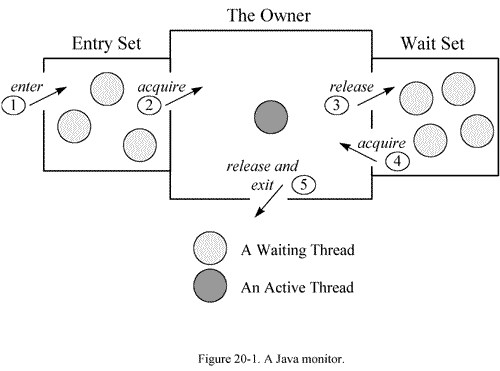
synchronized 的 monitor 机制
synchronized 的 monitor 机制 前言 本文基于 jdk 8 编写。author JellyfishMIX - github / blog.jellyfishmix.comLICENSE GPL-2.0 monitor monitor 是 synchronized 中用以实现线程之间的互斥与协作的主要手段,它可以看成是对象或者 class 持有的锁。每一个对象…...
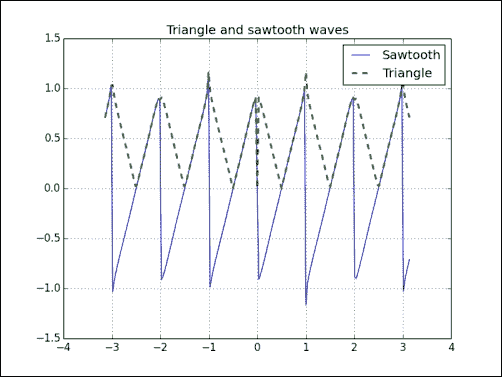
NumPy 初学者指南中文第三版:1~5
原文:NumPy: Beginner’s Guide - Third Edition 协议:CC BY-NC-SA 4.0 译者:飞龙 一、NumPy 快速入门 让我们开始吧。 我们将在不同的操作系统上安装 NumPy 和相关软件,并看一些使用 NumPy 的简单代码。 本章简要介绍了 IPython…...
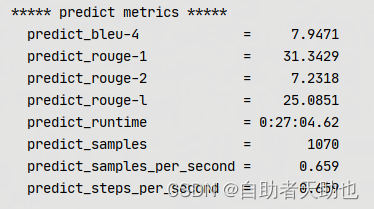
ChatGLM-6B论文代码笔记
ChatGLM-6B 文章目录 ChatGLM-6B前言一、原理1.1 优势1.2 实验1.3 特点:1.4 相关知识点 二、实验2.1 环境基础2.2 构建环境2.3 安装依赖2.4 运行2.5 数据2.6 构建前端页面 3 总结 前言 Github:https://github.com/THUDM/ChatGLM-6B 参考链接:…...
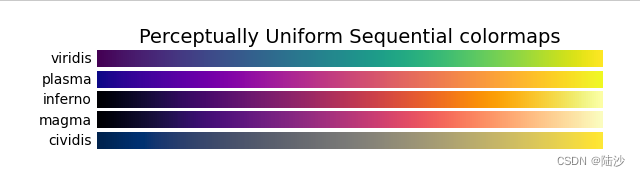
机器学习入门实例-加州房价预测-1(数据准备与可视化)
问题描述 数据来源:California Housing Prices dataset from the StatLib repository,1990年加州的统计数据。 要求:预测任意一个街区的房价中位数 缩小问题:superwised multiple regressiong(用到人口、收入等特征) univariat…...

【ROS2指南-20】了解ROS2组件的用法
在单个进程中组合多个节点 目录 背景 运行演示 发现可用组件 使用 ROS 服务 (1.) 与发布者和订阅者的运行时组合 使用 ROS 服务 (1.) 与服务器和客户端的运行时组合 使用 ROS 服务的编译时组合 (2.) 使用 dlopen 的运行时组合 使用启动动作组合 高级主题 卸载组件 重新…...
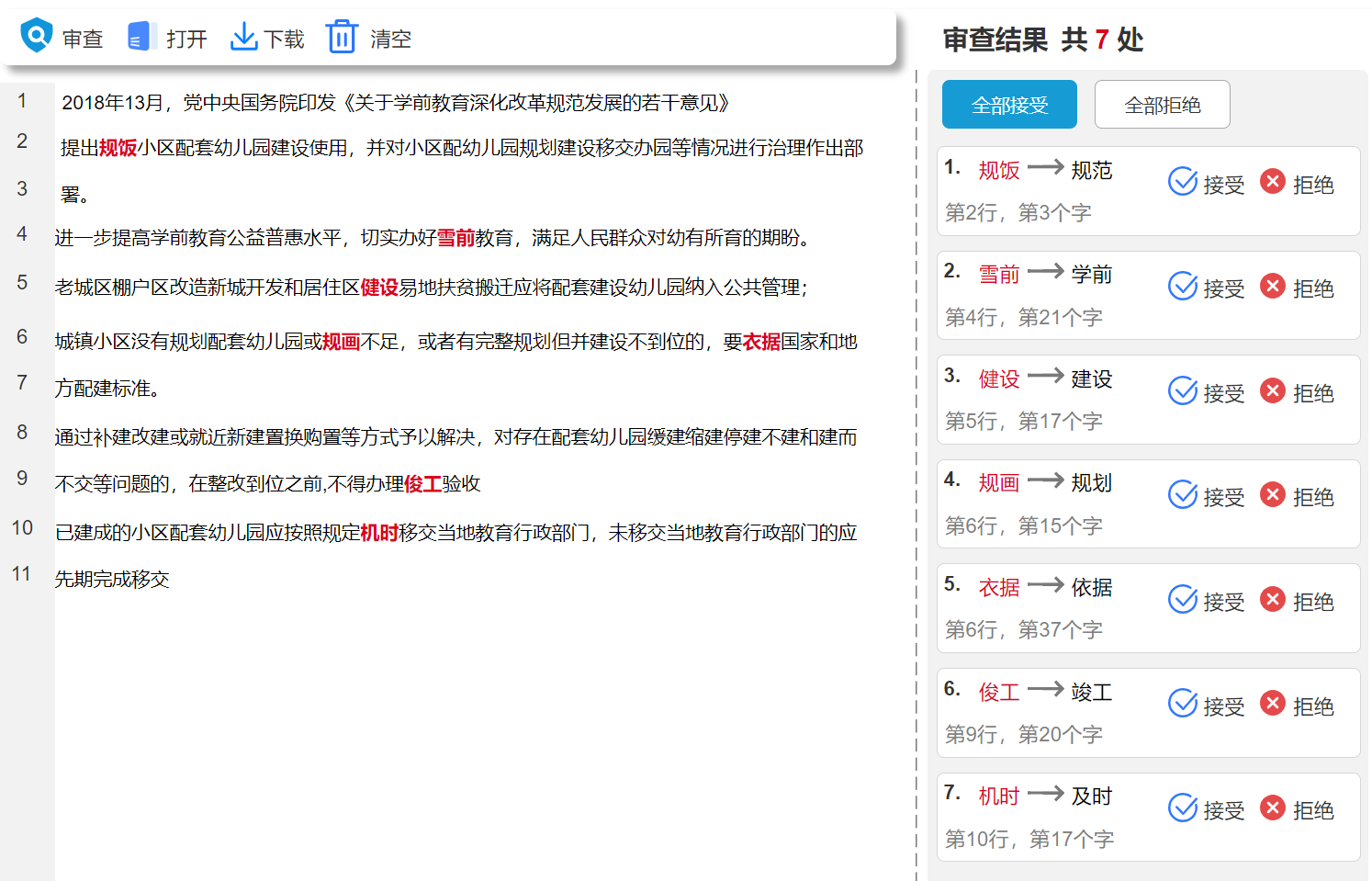
使用AI进行“文本纠错”
AI在现实中的应用有很多,你有没有想过,它还可以进行文本纠错呢?传统的校对既耗时又枯燥,通过“AI纠错”,不仅能更快完成,还能提高准确度。那么AI“文本纠错”背后的原理是什么呢?和我一起看看吧…...

第九章 法律责任与法律制裁
第九章 法律责任与法律制裁_副本 目录 第一节 法律责任的概念 一 法律责任的含义二 法律责任的特点 第二节 法律责任的分类与竞合 一 法律责任的分类 (一)根据责任行为所违反的法律的性质 民事责任:刑事责任行政责任违宪责任 (二…...

如何选择好用的海康视频恢复软件?综合考虑这几点
海康视频恢复通常是指从海康威视监控设备中恢复删除或丢失的视频。在使用海康设备进行监控时,一些重要的视频可能会被误删除或其他原因导致丢失,如果没有及时备份,数据就可能会“永久”丢失?其实不然,我们可以选择好用…...

前端学习:HTML颜色(什么是RGB、HEX、HSL)
一、什么是RGB、HEX、HSL? 无论是RGB、HEX、HSL,它们的作用只有一个:用数字表达出一种颜色。 1.RGB RGB通过输入的数值,将红色、绿色和蓝色的光源以一定的量混合在一起,形成颜色。 软件中通常让你输入Red、Green、B…...
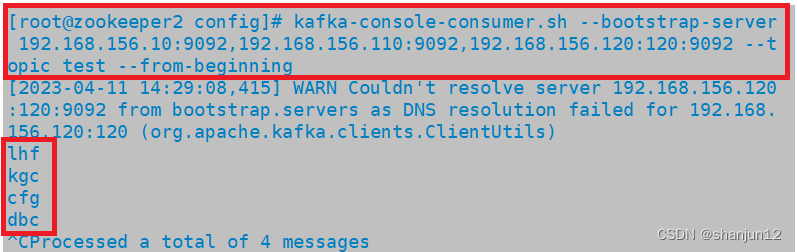
zookeeper + kafka集群搭建详解
目录 1.消息队列介绍 1.为什么需要消息队列 (MO) 2.使用消息队列的好处 3.消息队列的两种模式 2.Kafka相关介绍 1.Kafka定义 2.Kafka简介 3. Kafka的特性 3.Kafka系统架构 1. Broker(服务器) 2. Topic(一个队…...

【数据结构与算法】 - 双向链表 - 详细实现思路及代码
目录 一、概述 二、双向链表 三、双向链表实现步骤 📌3.1 C语言定义双向链表结点 📌3.2 双向链表初始化 📌3.3 双向链表插入数据 📌3.4 双向链表删除数据 📌3.5 双向链表查找数据 📌3.6 双向链…...

面试官在线点评4份留学生简历! 这些坑你中了几个?如何写项目描述才能被大厂发面试?转专业简历该咋写 | 还有优秀简历展示!
我们给大家展示一下 从材料的准备 也就是说到底包含哪些具体的项目 为什么说这些项目是不错的 第二呢就是说在陈述上 在整个这个简历的结构 他的完备性他的准确性 他的正确性 以及最后他的具体的这种项目的描述 那讲完了这个好的简历呢 我们另外搜集了几份简历 那这些简历呢其实…...
一觉醒后ChatGPT 被淘汰了
OpenAI 的 Andrej Karpathy 都大力宣传,认为 AutoGPT 是 prompt 工程的下一个前沿。 近日,AI 界貌似出现了一种新的趋势:自主人工智能。 这不是空穴来风,最近一个名为 AutoGPT 的研究开始走进大众视野。特斯拉前 AI 总监、刚刚回归…...

spring框架的事务
1.什么是事务? 事务:是数据库操作的最小工作单元,是作为单个逻辑工作单元执行的一系列操作;这些操作作为一个整体一起向系统提交,要么都执行、要么都不执行;事务是一组不可再分割的操作集合(工作逻辑单元…...

Spring配置数据源
Spring配置数据源数据源的作用环境准备手动创建c3p0数据源封装抽取关键信息,手动创建c3p0数据源使用Spring容器配置数据源数据源的作用 数据源(连接池)是提高程序性能如出现的 事先实例化数据源,初始化部分连接资源 使用连接资源时从数据源中获取 使用完…...

【前端之旅】Vue入门笔记
一名软件工程专业学生的前端之旅,记录自己对三件套(HTML、CSS、JavaScript)、Jquery、Ajax、Axios、Bootstrap、Node.js、Vue、小程序开发(Uniapp)以及各种UI组件库、前端框架的学习。 【前端之旅】Web基础与开发工具 【前端之旅】手把手教你安装VS Code并附上超实用插件…...
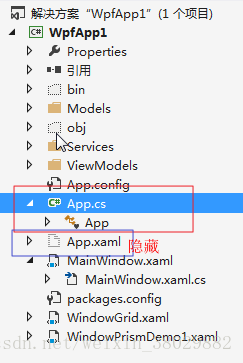
WPF教程(二)--Application WPF程序启动方式
1.Application介绍 WPF与WinForm一样有一个 Application对象来进行一些全局的行为和操作,并且每个 Domain (应用程序域)中仅且只有一个 Application 实例存在。和 WinForm 不同的是WPF Application默认由两部分组成 : App.xaml 和 App.xaml.…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
