【洛谷】P1631 序列合并
【洛谷】 P1631 序列合并
题目描述
有两个长度为 N N N 的单调不降序列 A , B A,B A,B,在 A , B A,B A,B 中各取一个数相加可以得到 N 2 N^2 N2 个和,求这 N 2 N^2 N2 个和中最小的 N N N 个。
输入格式
第一行一个正整数 N N N;
第二行 N N N 个整数 A 1 , A 2 , … , A N A_1,A_2,…,A_N A1,A2,…,AN。
第三行 N N N 个整数 B 1 , B 2 , … , B N B_1,B_2,…,B_N B1,B2,…,BN。输出格式
一行 N N N 个整数,从小到大表示这 N N N 个最小的和。
样例输入 #1
3
2 6 6
1 4 8样例输出 #1
3 6 7提示
对于 50 % 50\% 50% 的数据, N ≤ 1 0 3 N \le 10^3 N≤103。
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 1 0 5 1 \le N \le 10^5 1≤N≤105, 1 ≤ a i , b i ≤ 1 0 9 1 \le a_i,b_i \le 10^9 1≤ai,bi≤109。
题解
对于输入的两个数组 A = { a i ∣ i = 1 , 2 , … N } , B = { b i ∣ i = 1 , 2 , … N } A=\{a_i | i=1,2,…N\},B=\{b_i | i=1,2,…N\} A={ai∣i=1,2,…N},B={bi∣i=1,2,…N},最直接的方法是用一个规格为 N × N N×N N×N 的数组去存放所有的 a i + b j a_i +b_j ai+bj ,然后可采用基于选择排序的思路去选出前 N N N 个最小的值。但是这样求解的时间复杂度为 O ( N 3 ) O(N^3 ) O(N3) ,这将难以通过全部测试数据。因此需要想别的办法。
如果你足够敏感,你应该会立刻想到一个数据结构——堆。堆是一种建立为 O ( n ) O(n) O(n) 级、插入和删除都为 O ( l o g n ) O(logn) O(logn) 级的数据结构。显然,在面对 N × N N×N N×N 个数据时,用他们直接建立规格为 N × N N×N N×N 的堆依然有可能超时(此时的时间复杂度为 O ( N 2 ) O(N^2) O(N2)),因此需考虑别的方法。试想,我们能否能利用堆的这种具有快速修改能力的数据结构来动态构建一个长度为 N N N 的数据结构,并通过某种较为快速的取值方式对 N × N N×N N×N 个数据进行快速扫描并取值以更新该数据结构。为此,引入偏序集:
构建偏序集要求输入的数组有序。观察题中的两个数组: [ a 1 , a 2 , … , a N ] , [ b 1 , b 2 , … , b N ] [a_1,a_2,…,a_N],[b_1,b_2,…,b_N] [a1,a2,…,aN],[b1,b2,…,bN] ,它们的长度都为 N N N,对这两个数组分别排序的时间复杂度(最快)为 O ( N l o g N ) O(N logN) O(NlogN) ,这是能接受的。当输入的两个数组均有序时,由所有的 a i + b j a_i +b_j ai+bj 便可以组成以下 N N N 个偏序集:
{ a 1 + b 1 , a 1 + b 2 , … , a 1 + b N } { a 2 + b 1 , a 2 + b 2 , … , a 2 + b N } … … { a N + b 1 , a N + b 2 , … , a N + b N } \{ a_1+b_1, a_1+b_2, … ,a_1+b_N \} \\ \{ a_2+b_1, a_2+b_2, … ,a_2+b_N \} \\ …… \\ \{ a_N+b_1, a_N+b_2, … ,a_N+b_N \} {a1+b1,a1+b2,…,a1+bN}{a2+b1,a2+b2,…,a2+bN}……{aN+b1,aN+b2,…,aN+bN}
显然,在这 N N N 个偏序集中,其都是有序的(单调递增),因此,对每个单独的偏序集而言,其始终满足:
a i + b j ≤ a i + b ( j + 1 ) a_i+b_j≤ a_i+b_{(j+1)} ai+bj≤ai+b(j+1)
同时,可断言 a 1 + b 1 a_1+b_1 a1+b1 为所有 a i + b j a_i+b_j ai+bj 组合中的最小值; a N + b N a_N+b_N aN+bN 为所有 a i + b j a_i+b_j ai+bj 组合中的最大值;每个偏序集中的最小值为 a i + b 1 ( i = 1 , 2 , … , N ) a_i+b_1 (i=1,2,…,N) ai+b1(i=1,2,…,N) 、最大值为 a i + b N ( i = 1 , 2 , … , N ) a_i+b_N (i=1,2,…,N) ai+bN(i=1,2,…,N) ;不同偏序集对应同一列的元素中始终有 a i + b j ≤ a ( i + 1 ) + b j a_i+b_j≤ a_{(i+1)}+b_j ai+bj≤a(i+1)+bj 。
基于偏序集的这一特性,我们就能在 O ( 1 ) O(1) O(1) 的时间复杂度内,从构建好的偏序集中取出当前最小值。具体的取值策略如下(假设现在有一个已经构建好的长度为 N N N 的小根堆 h e a p heap heap ):
- 1、把每个偏序集中的最小元素加入小根堆 h e a p heap heap 中,即 h e a p = { a 1 + b 1 , a 2 + b 1 , … , a N + b 1 } heap=\{a_1+b_1,a_2+b_1,…,a_N+b_1\} heap={a1+b1,a2+b1,…,aN+b1} ;
- 2、从小根堆 h e a p heap heap 中取出根元素(即当前堆里的最小值),假设取出的元素为 a i + b j a_i+b_j ai+bj,记弹出数 +1;
- 3、从取出元素所在偏序集中,取出仅比其小的元素(即 a i + b ( j + 1 ) a_i+b_{(j+1)} ai+b(j+1)),将其插入小根堆 h e a p heap heap 中;
- 4、若弹出数不为 N N N,则继续执行 2;否则结束取值。
当此算法结束时,我们就取出了所有 a i + b j a_i+b_j ai+bj 组合中的前 N N N小值。
正确性证明
加入偏序集元素的顺序使得我们能保证当前加入的元素是该偏序集中最小的,而小根堆 h e a p heap heap 又能保证每次取出的元素是 N N N 个偏序集中未取的最小的元素中最小的,所以正确性得证。
STL 模板的使用
需要注意的是:在实际编码时,我们不必手动构建一个堆,而可以通过调用 STL 中的模板函数、数据结构来直接使用。优先队列priority_queue正是一个由 STL 提供的模板容器,该队列具有普通队列所具备的一切功能,不同的是,优先队列采用了“堆”这一数据结构,保证了该队列中的第一个元素总是整个优先队列中最大的(或最小的)元素(默认是大根堆)。
priority_queue 类的模板参数列表有三个参数:
class T,T 是优先队列中存储的元素的类型;class Container = vector<T>,Container 是优先队列底层使用的存储结构,可以看出来,默认采用 vector;class Compare = less<typename Container::value_type> Compar,是定义优先队列中元素比较方式的类。什么是优先队列中元素的比较方式?前面曾提到,优先队列的底层容器其实就是堆,而堆中元素是存在大小关系的。比如大根堆:每个结点的值都不大于它的父结点,因此其堆顶元素是最大的。当我们自己定义了某些类,并将由该类实例化得到的对象存进堆中时(此时堆里的元素就是某个对象),这时堆中元素的比较方式自然会发生改变。而编译器中的比较类只能比较内置类型,所以这时就需要用户给出一个用于比较大小的模式(即自定义类的比较方式),并将其填充到 Compare 参数的位置。
注:class Compare后跟着的less<typename Container::value_type>就是默认的比较类,默认是按小于(less)的方式比较,这种比较方式创建出来的是大根堆(所以优先队列默认为大根堆)。如果需要创建小堆,就需要将 less 改为 greater。
less<typename Container::value_type>的定义如下:
template <class T>
struct less: binary_function <T,T,bool> {bool operator() (const T& x, const T& y) const {return x<y;}
};
greater<typename Container::value_type>的定义如下:
template <class T>
struct greater: binary_function <T,T,bool> {bool operator() (const T& x, const T& y) const {return x>y;}
};
在这两个函数内部都重载了“( )”,从而构成仿函数以便使用。
方法一
前面的算法曾提到一点:当从优先队列中取出某个元素 a i + b j a_i+b_j ai+bj 时,需要从该元素所在偏序集中取出仅次(小)于该元素的另一个元素 a i + b ( j + 1 ) a_i+b_{(j+1)} ai+b(j+1) 填补进优先队列。理论上是这样进行取值,但实际操作时,我们不可能真的去建立一个 N × N N×N N×N 的二维数组(作为偏序集),因为这存在爆内存的可能。那要通过怎样的方式来完成这一功能呢?
回看对偏序集的取数操作,不难发现一点:当从优先队列中弹出某个元素 a i + b j a_i+b_j ai+bj 时,该元素存在两个索引(即 i i i 和 j j j ),其中第一个索引 i i i 指示了接下来要在 A 数组中取值的索引,第二个索引在执行 j + 1 j+1 j+1 后指示了接下来要在 B 数组中取值的索引。因此,我们实际上只需要再建立 N N N 个数对(为长度为N的优先队列中的每个元素各配置一个),就能完成从偏序集中取所需值的需求。
对于此结构(含:当前数的值 value、对应在A中索引 ida、对应在B中的索引 idb,共三个属性),因为他足够简单,因此我们可以自行构建结构体。但是需要注意一点:由于这个类型的数据会被放进优先队列中,因此需要为该结构指明一种比较大小的方式(当然,这里比较的肯定是 value),这就需要重载比较运算符;更进一步,我们要求此优先队列是“小根堆”,因此要重载的运算符是“>”。下面给出基于该思路写出的 AC 代码:
#include<bits/stdc++.h>
using namespace std;// 数据声明
const int N = 100005;
int n,k,a[N],b[N];// 自定义数据结构
struct NODE {int value, ida, idb;// 重载运算符bool operator>(const NODE &obj) const { return value > obj.value;}
}node;// 定义优先队列
priority_queue<NODE,vector<NODE>,greater<NODE> > q;int main(){// 录入数据 cin>>n;for (int i=0; i<n; i++) cin>>a[i];for (int i=0; i<n; i++) cin>>b[i];// 对数组排序 sort(a, a+n);sort(b, b+n);// 初始化优先队列 for (int i = 0; i<n; i++)q.push({a[i]+b[0], i, 0});while(n--){// 取出当前队列的最小值 node=q.top(), q.pop();// 输出 cout<<node.value<<" ";// 从取出元素所在偏序集中选出其次元素(并更改索引 idb 值) node.value = a[node.ida] + b[++node.idb];// 入队列 q.push(node);}return 0;
}方法二
都说 STL 是个大暖男,这道题为此提供了充分的论据。
STL 提供了一个表达“数对”含义的数据结构 pair,其相关属性和函数定义如下:
- 构造函数
pair<type1, type2>obj(value1, value2):此函数可以声明并定义一个pair对象; - 套娃函数
make_pair( obj1, obj2):此函数可以将两个已存在的对象构造为一个新的pair类型; first属性:pair_obj.first 可取出对象 pair_ obj 中的第一个属性值;second属性:pair_obj.second 可取出对象pair_ obj 中的第二个属性值。
根据前面的分析我们知道,现在需要一个含 3 个 int 类型组合在一起的数据结构,而 pair 结构体能够建立一个含两个元素的类。因此,为了能多加一个元素进去,我们可以再多建立一重(就像套娃一样再多一重)pair,即建立:pair<int, pair<int, int>> obj。这样一来,我们可设各层属性表达的含义如下:
- obj.first // 表示 value
- obj.second.first; // 表示 ida
- obj.second.second // 表示 idb
如此,就能根据前面的思路写出求解本题的完整代码:
#include<bits/stdc++.h>
using namespace std;// 数据声明
const int MAX = 100005;
int a[MAX], b[MAX];priority_queue<pair<int,pair<int,int> >,vector< pair<int,pair<int,int> > >,greater< pair<int,pair<int,int> > > > q;int main(){int n, tmpa, tmpb;// 录入数据 cin>>n;for(int i=0;i<n;i++) cin>>a[i];for(int i=0;i<n;i++) cin>>b[i];// 对数组排序sort(a, a+n);sort(b, b+n); for(int i=0;i<n;i++) q.push(make_pair(a[i]+b[0], pair<int,int>(i, 0)));// 查找前 k 小值 while(n--){// 输出 cout<<q.top().first<<" ";// 取出 ida 和 idb 索引 tmpa = q.top().second.first;tmpb = q.top().second.second;// 第一个元素出栈 q.pop();// 更改取出元素所在偏序集中的次元素入栈 q.push(make_pair(a[tmpa]+b[tmpb+1], pair<int,int>(tmpa, tmpb+1)));}return 0;
}
END
相关文章:

【洛谷】P1631 序列合并
【洛谷】 P1631 序列合并 题目描述 有两个长度为 N N N 的单调不降序列 A , B A,B A,B,在 A , B A,B A,B 中各取一个数相加可以得到 N 2 N^2 N2 个和,求这 N 2 N^2 N2 个和中最小的 N N N 个。 输入格式 第一行一个正整数 N N N; 第二…...
2023年七大最佳勒索软件解密工具
勒索软件是目前最恶毒且增长最快的网络威胁之一。作为一种危险的恶意软件,它会对文件进行加密,并用其进行勒索来换取报酬。 幸运的是,我们可以使用大量的勒索软件解密工具来解锁文件,而无需支付赎金。如果您的网络不幸感染了勒索软…...

prettier 命令行工具来格式化多个文件
prettier 命令行工具来格式化多个文件 你可以使用 prettier 命令行工具来格式化多个文件。以下是一个使用命令行批量格式化文件的示例: 安装 prettier 如果你还没有安装 prettier,你可以使用以下命令安装它: npm install -g prettier 进入…...
我发现了PMP通关密码!这14页纸直接背!
一周就能背完的PMP考试技巧只有14页纸 共分成了4大模块 完全不用担心看不懂 01关键词篇 第1章引论 1.看到“驱动变革”--选项中找“将来状态” 2.看到“依赖关系”--选项中找“项目集管理” 3.看到“价值最大化”--选项中找“项目组合管理” 4.看到“可行性研究”--选项中…...
Medical X-rays Dataset汇总(长期更新)
目录 ChestX-ray8 ChestX-ray14 VinDr-CXR VinDr-PCXR ChestX-ray8 ChestX-ray8 is a medical imaging dataset which comprises 108,948 frontal-view X-ray images of 32,717 (collected from the year of 1992 to 2015) unique patients with the text-mi…...

一文告诉你如何做好一份亚马逊商业计划书的框架
“做亚马逊很赚钱”、“我也来做”、“哎,亏钱了”诸如此类的话听了实在是太多。亚马逊作为跨境电商老大哥,许多卖家还是对它怀抱着很高的期许。但是,事实的残酷的。有人入行赚得盆满钵盈,自然也有人亏得血本无归。 会造成这种两…...

原来ChatGPT可以充当这么多角色
充当 Linux 终端 贡献者:f 参考:https ://www.engraved.blog/building-a-virtual-machine-inside/ 我想让你充当 linux 终端。我将输入命令,您将回复终端应显示的内容。我希望您只在一个唯一的代码块内回复终端输出,而不是其他任…...
数据结构_第十三关(3):归并排序、计数排序
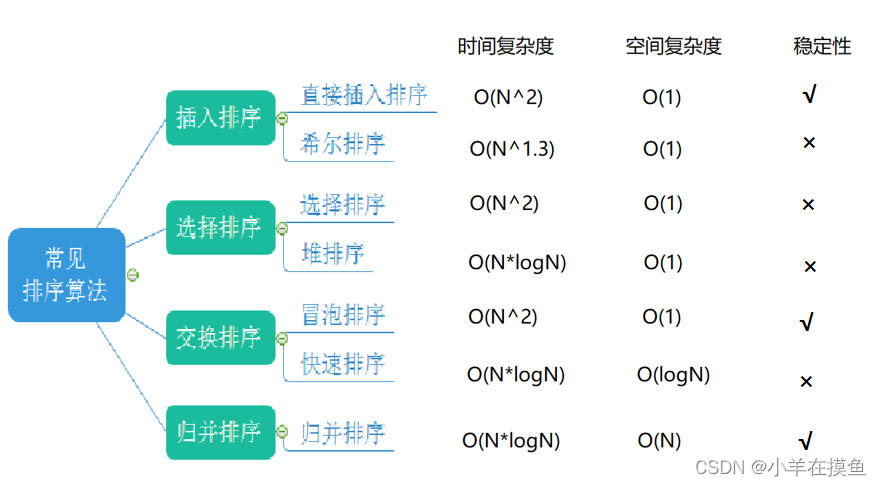
目录 归并排序 1.基本思想: 2.原理图: 1)分解合并 2)数组比较和归并方法: 3.代码实现(递归方式): 4.归并排序的非递归方式 原理: 情况1: 情况2&…...

“成功学大师”杨涛鸣被抓
我是卢松松,点点上面的头像,欢迎关注我哦! 4月15日,号称帮助一百多位草根开上劳斯莱斯,“成功学大师”杨涛鸣机其团队30多人已被刑事拘留,培训课程涉嫌精神传销,警方以诈骗案进行立案调查。 …...
【hello C++】内存管理
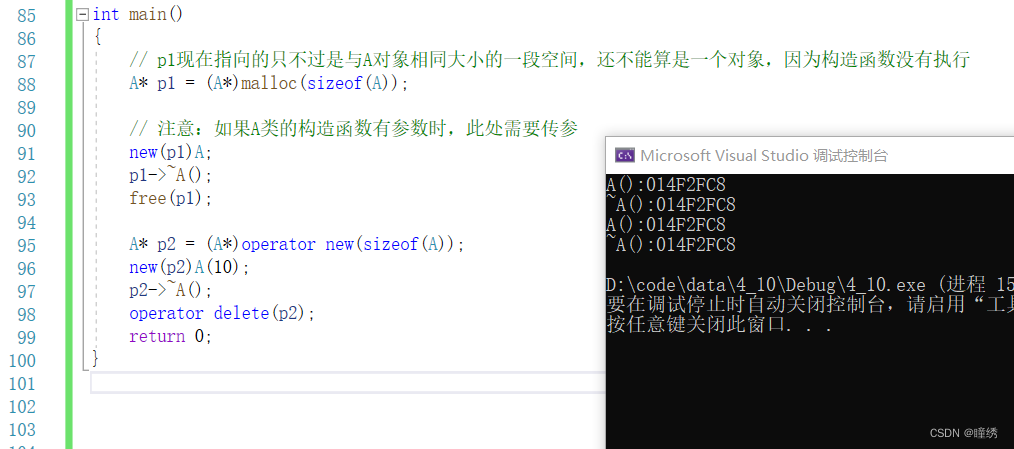
目录 前言: 1. C/C内存分布 2. C语言动态内存管理方式 3. C内存管理方式 3.1 new / delete 操作内置类型 3.2 new和delete操作自定义类型 4. operator new与operator delete函数 4.1 operator new与operator delete函数 5. new和delete的实现原理 5.1 内置类型 5.2…...
)
AppArmor零知识学习十二、源码构建(9)
本文内容参考: AppArmor / apparmor GitLab 接前一篇文章:AppArmor零知识学习十一、源码构建(8) 在前一篇文章中完成了apparmor源码构建的第六步——Apache mod_apparmor的构建和安装,本文继续往下进行。 四、源码…...

Unity - 带耗时 begin ... end 的耗时统计的Log - TSLog
CSharp Code // jave.lin 2023/04/21 带 timespan 的日志 (不帶 log hierarchy 结构要求,即: 不带 stack 要求)using System; using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEngine;public…...

Python 智能项目:1~5
原文:Intelligent Projects Using Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何实…...

C++设计模式:面试题精选集
目录标题 引言(Introduction)面试的重要性设计模式概述面试题的选择标准 设计模式简介 面试题解析:创建型模式(Creational Patterns Analysis)面试题与解答代码实例应用场景分析 面试题解析:结构型模式&…...

蓝桥 卷“兔”来袭编程竞赛专场-10仿射加密 题解
赛题介绍 挑战介绍 仿射密码结合了移位密码和乘数密码的特点,是一种替换密码。它是利用加密函数一个字母对一个字母的加密。加密函数是 yaxb(mod m) ,且 a,b∈Zm (a、b 的值在 m 范围内),且 a、m 互质。 m 是字符集的…...

android so库导致的闪退及tombstone分析
android中有3种crash情况:未捕获的异常、ANR和闪退。未捕获的异常一般用crash文件就可以记录异常信息,而ANR无响应表现就是界面卡着无法响应用户操作,而闪退则是整个app瞬间退出,个人感觉对用户造成的体验最差。闪退一般是由于调用…...

图结构基本知识
图 1. 相关概念2. 图的表示方式3. 图的遍历3.1 深度优先遍历(DFS)3.2 广度优先遍历(BFS) 1. 相关概念 图G(V,E) :一种数据结构,可表示“多对多”关系,由顶点集V和边集E组成;顶点(ve…...

Hibernate 的多种查询方式
Hibernate 是一个开源的 ORM(对象关系映射)框架,它可以将 Java 对象映射到数据库表中,实现对象与关系数据库的映射。Hibernate 提供了多种查询方式,包括 OID 检索、对象导航检索、HQL 检索、QBC 检索和 SQL 检索。除此…...
FreeRTOS 任务调度及相关函数详解(一)
文章目录 一、任务调度器开启函数 vTaskStartScheduler()二、内核相关硬件初始化函数 xPortStartScheduler()三、启动第一个任务 prvStartFirstTask()四、中断服务函数 xPortPendSVHandler()五、空闲任务 一、任务调度器开启函数 vTaskStartScheduler() 这个函数的功能就是开启…...
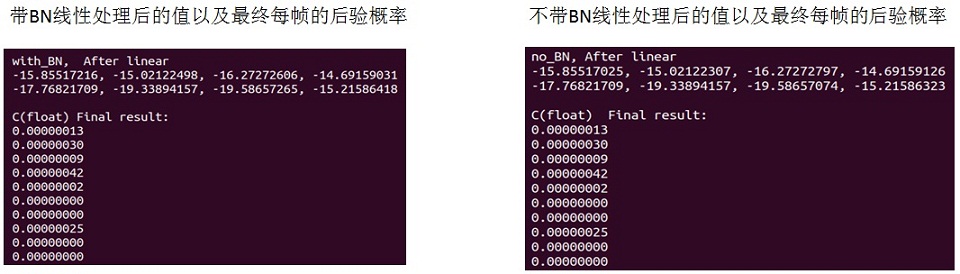
飞桨paddlespeech语音唤醒推理C实现
上篇(飞桨paddlespeech 语音唤醒初探)初探了paddlespeech下的语音唤醒方案,通过调试也搞清楚了里面的细节。因为是python 下的,不能直接部署,要想在嵌入式上部署需要有C下的推理实现,于是我就在C下把这个方…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...
