数据结构_第十三关(3):归并排序、计数排序
目录
归并排序
1.基本思想:
2.原理图:
1)分解合并
2)数组比较和归并方法:
3.代码实现(递归方式):
4.归并排序的非递归方式
原理:
情况1:
情况2:
情况3:
非递归代码实现
归并排序的特性总结:
计数排序
基本思想:
算法原理:
算法升级
计算排序的特点:
代码实现
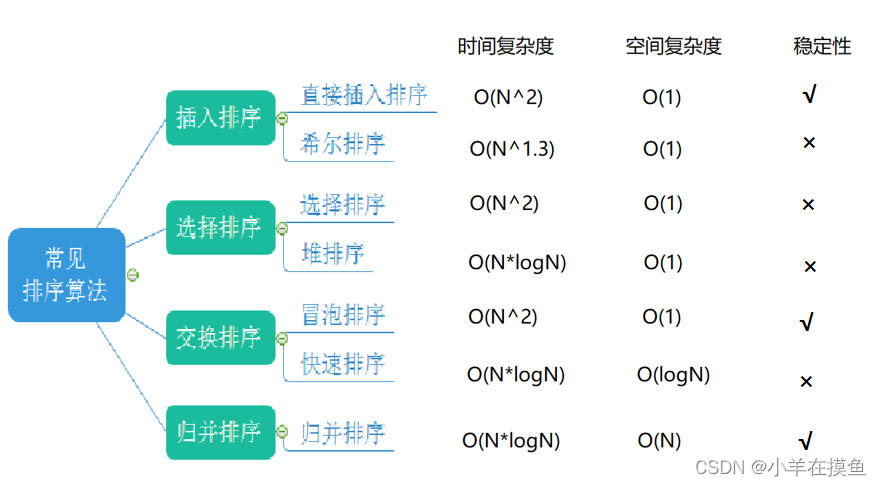
排序算法复杂度及稳定性分析
什么时稳定性?
各种常见排序算法的总结
归并排序
1.基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,
该算法是采用分治法(Divide andConquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;
即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为二路归并。
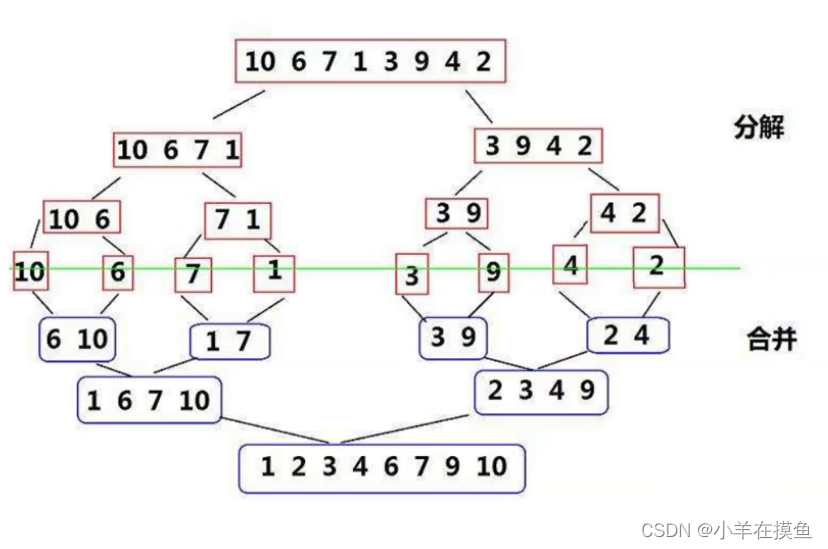
2.原理图:
1)分解合并
第一层将一个数组分两个大组,
第二层再继续分,直到分成每组都只有一个为止
分解完了之后就是进行合并,每两个小数组,按顺序合并成一个大的数组
最终,合并称为一个有序的集合
动图效果:
归并排序是在原数组上进行的,用一个临时数组来做归并,把归并好的元素复制回原数组
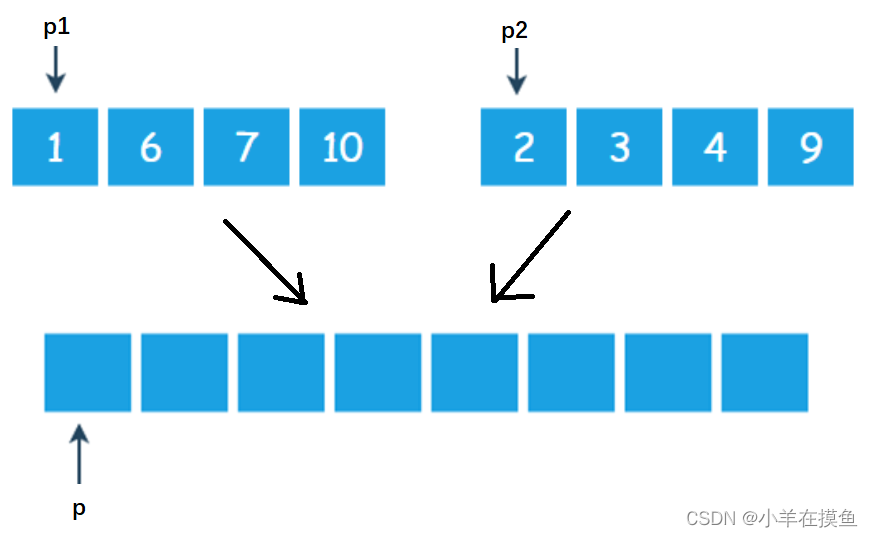
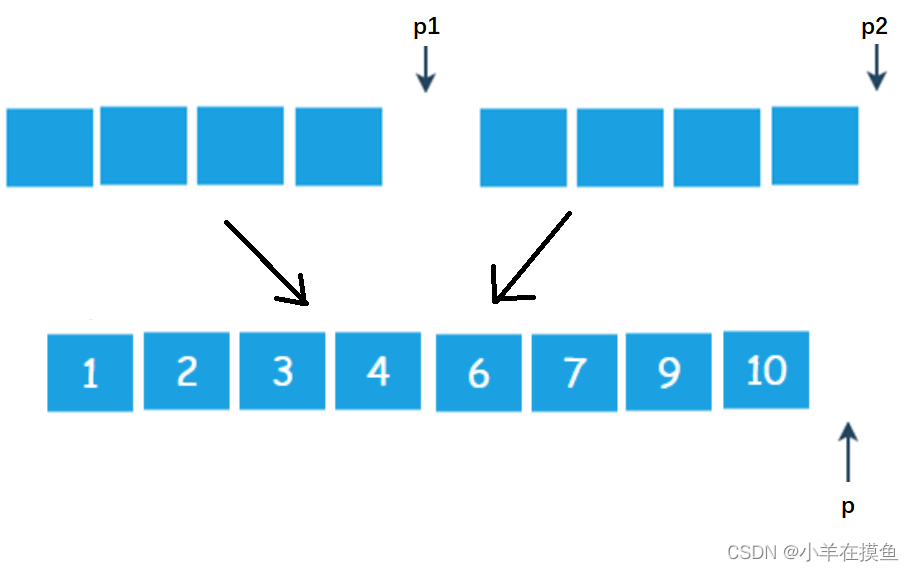
2)数组比较和归并方法:
用上述长度为4的集合举例:
第一步:比较p1和p2位置元素的大小,谁的小,将谁的值放到p位置,并将指向小的元素的那个指针++,并且将p++
1比2小,放1到p位置,p1++,p++
......
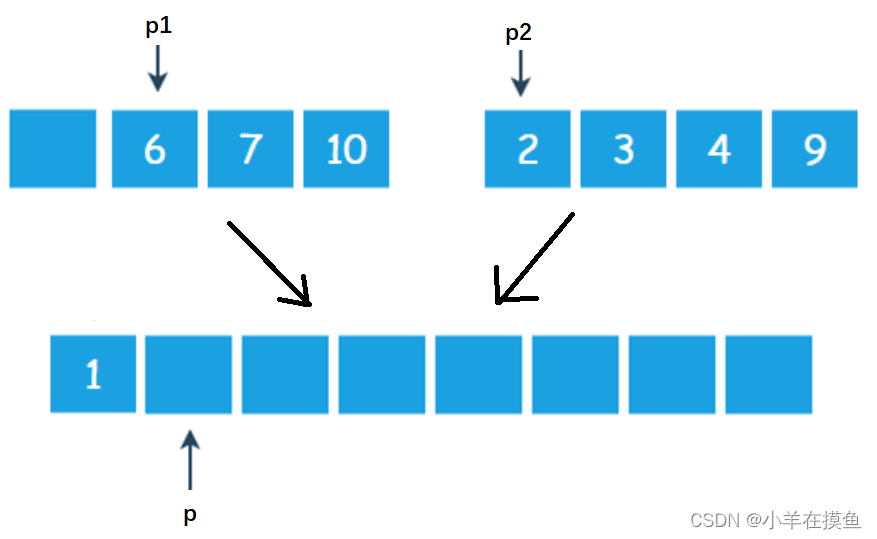
第二步:按第一步的步骤,逐一比较,直到有一个指针走到了集合之外如下:
此时p2已经走到了集合外,就可以退出循环了
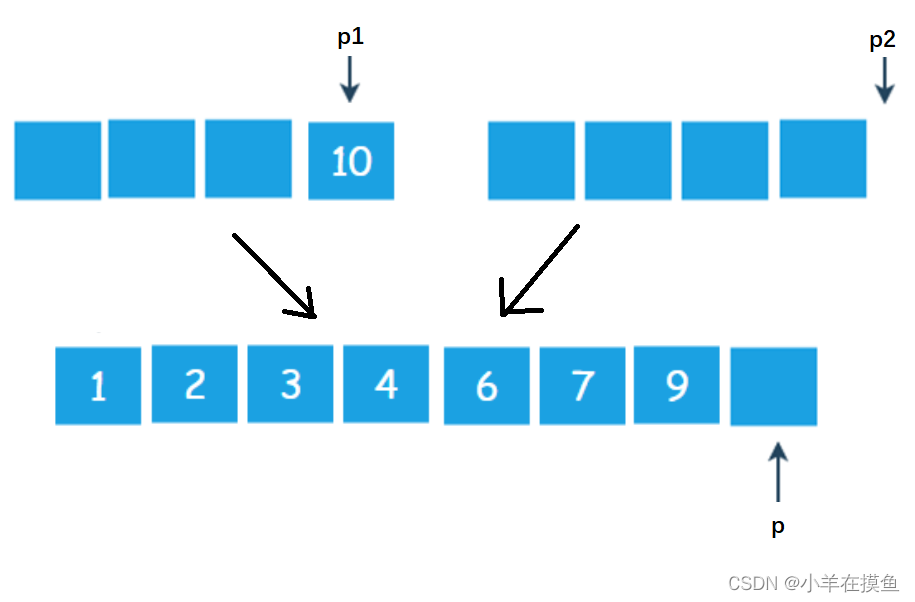
第三步:放一个循环,将没走完的那个集合的剩余元素按顺序放到大集合种即可
当p走到大集合外面时结束循环
3.代码实现(递归方式):
//归并排序(递归实现)//归并子函数
//(在遇到需要malloc扩容的函数时,将malloc代码放入主函数,另写一个子函数用来完成递归)
void _MergeSort(int* a, int begin ,int end, int* temp)
{//最后只剩下一个数的时候就说明begin=end,返回if (begin >= end){return;}int mid = (begin + end) / 2;//[begin, mid] [mid+1, end] 递归让子区间都有序_MergeSort(a, begin, mid, temp); //递归左半区_MergeSort(a, mid+1, end, temp); //递归右半区//归并int begin1 = begin, end1 = mid; //左区间[begin1, end1]int begin2 = mid + 1, end2 = end; //右区间[begin2, end2]int i = begin;//如果左右两个区间都没有结束就继续,只要有一个区间结束就终止while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){temp[i++] = a[begin1++]; }else{temp[i++] = a[begin2++];}}//将没走到头的区间按顺序放到后面while (begin1 <= end1){temp[i++] = a[begin1++];}while (begin2 <= end2){temp[i++] = a[begin2++];}//将临时区间的数据拷贝回原数组memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
}//归并主函数
void MergeSort(int* a, int n)
{int* temp = (int*)malloc(sizeof(int) * n);if (temp == NULL){perror("malloc fail");exit(-1);}_MergeSort(a, 0, n-1, temp);free(temp);temp = NULL;
}4.归并排序的非递归方式
原理:
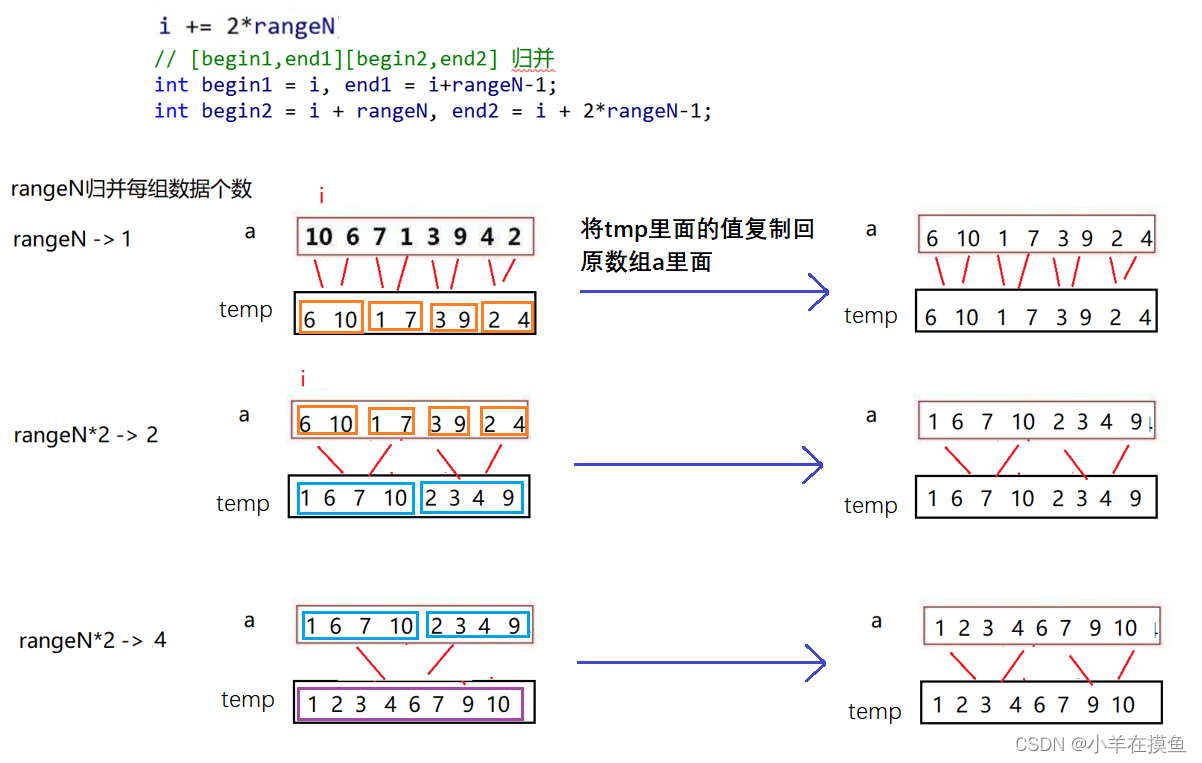
控制每次参与归并的元素即可,可以先定义一个变量rangeN,让其来划分区域
开始时rangeN=1,区域为1则是有序,
i = i + 2*rangeN 定义 i 来区分每块区域
左区域:[begin1,end1] 右区域:[begin2,end2]
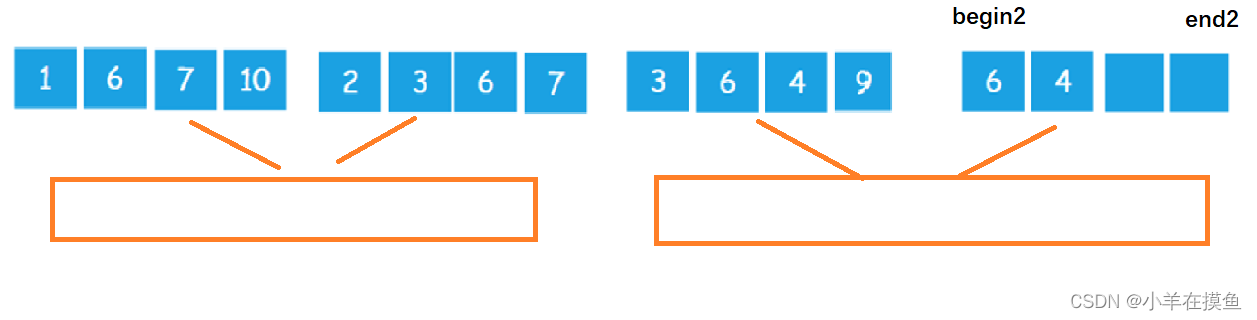
上图情况是一个特殊情况,如果遇到不能被完全划分左右区域对称的情况分为以下三种:
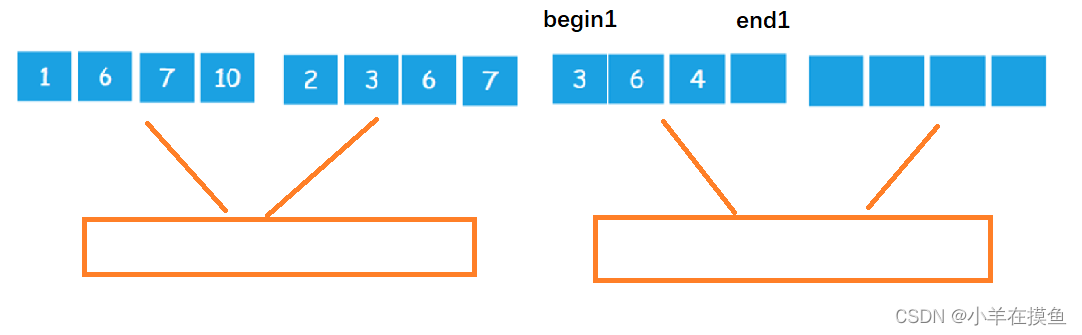
情况1:
当最后一个区域进行归并时,最后一组的左区间越界,所以需要对左区间的end1进行控制
情况2:
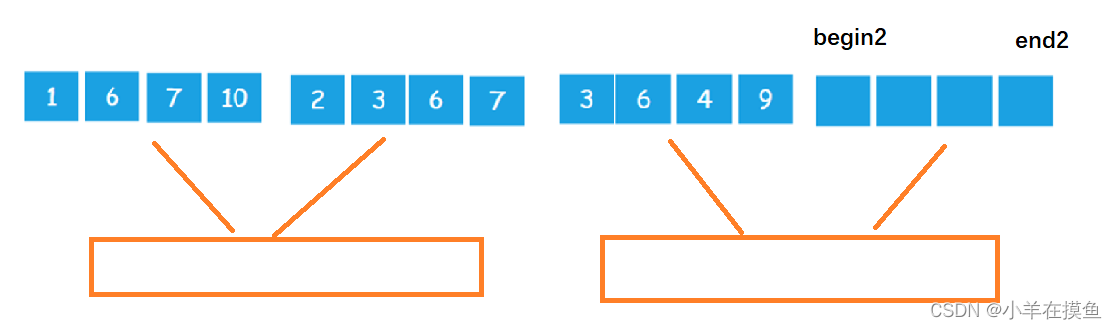
当最后一个区域进行归并时,最后一组的右区间全部越界,所以需要对右区间的begin2进行控制
情况3:
当最后一个小组进行归并时,由于右区间越界,所以我们需要对右区间end2进行控制
非递归代码实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);if (tmp == NULL){perror("malloc fail");exit(-1);}// 归并每组数据个数,从1开始,因为1个认为是有序的,可以直接归并int rangeN = 1;while (rangeN < n) {for (int i = 0; i < n; i += 2 * rangeN){// [begin1,end1][begin2,end2] 归并int begin1 = i, end1 = i + rangeN - 1;int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;int j = i;// end1 begin2 end2 越界的三种情况//一定需要按顺序进行判断,不然会出错//end1越界,情况1,//解决:直接退出本次循环,可以不让后面的进行归并,再下一次循环时再排序if (end1 >= n){break;}//begin2出界,情况2,//解决:直接退出本次循环,可以不让后面的进行归并,再下一次循环时再排序else if (begin2 >= n){break;}//end2越界,情况3//解决:让end2等于数组最后的下标else if (end2 >= n){end2 = n - 1;}//开始按顺序归并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}// 归并一部分,拷贝一部分memcpy(a + i, tmp + i, sizeof(int)*(end2 - i + 1));}rangeN *= 2;}free(tmp);tmp = NULL;
}归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,
归并排序的思考更多的是解决在磁盘中的外排序问题。- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
计数排序
基本思想:
之前学习的排序,无论是希尔排序,还是堆排序,都用的是比较两个数大小的方式进行的排序
而计数排序不是用比较的方法来进行排序的,它利用的是数组下标的计数来进行的排序
具体实现方法如下:
算法原理:
现假设有一组0~4的数据需要排序:{ 2,3,3,4,0,3,2,4,3 }
创建一个临时数组temp来依次记录每个数的出现次数
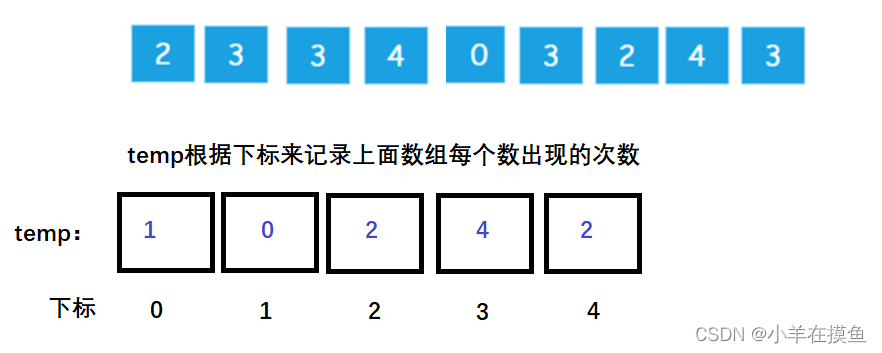
原数组中,
0出现了1次,就在temp下标为0的位置记录1
1没有出现, 就在temp下标为1的位置记录0
2出现了2次,就在temp下标为0的位置记录2
3出现了4次,就在temp下标为0的位置记录3
4出现了2次,就在temp下标为0的位置记录2
数组每一个下标位置的值,代表了数列中对应整数出现的次数。
有了这个 “统计结果”,排序就很简单了。
直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次:
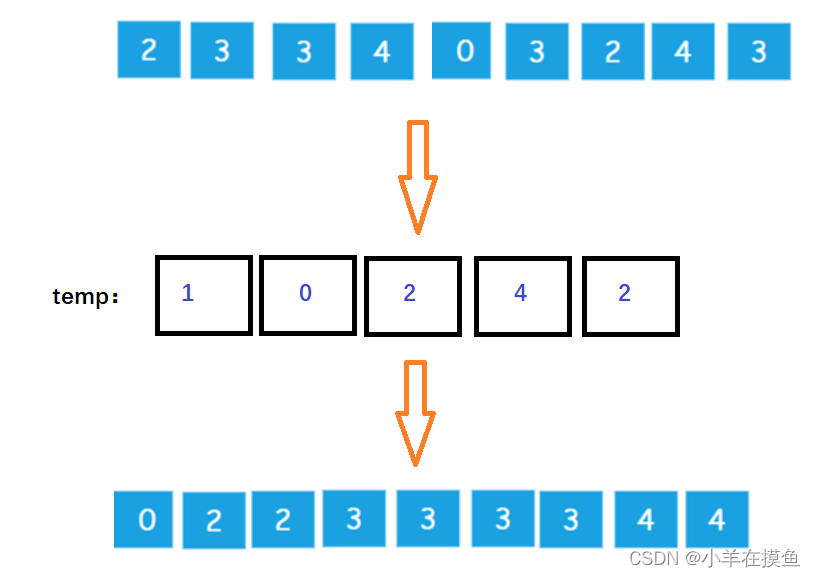
这样就能得到一个有序序列了
这就是计数排序的过程,因为他没有进行数与数之间的比较,
所以他的性能甚至快过那些O( log N) 的排序
可以看到上面的排序是一种特殊情况,那如果我们要排序的数组是 9000~9009,那么是不是得浪费前九千多个空间?
又或者是在原数组里面有负数的情况下是不是九不能进行计数排序了?
这就要对现有的算法进行一些小小的升级了
算法升级
例如我们有一组这样的数:9004,9001,9002,9005,9004,9001
这个数组,最大是9005,但最小的数是9001,如果用长度为9005的数组,那么按照上面的方法排序,肯定会太过浪费
事实上我们只需要开辟大小为5的数组即可(最大数 - 最小数 + 1)9005 - 9001 +1 = 5
用下标为0的记录9001,用下标为4的记录9005
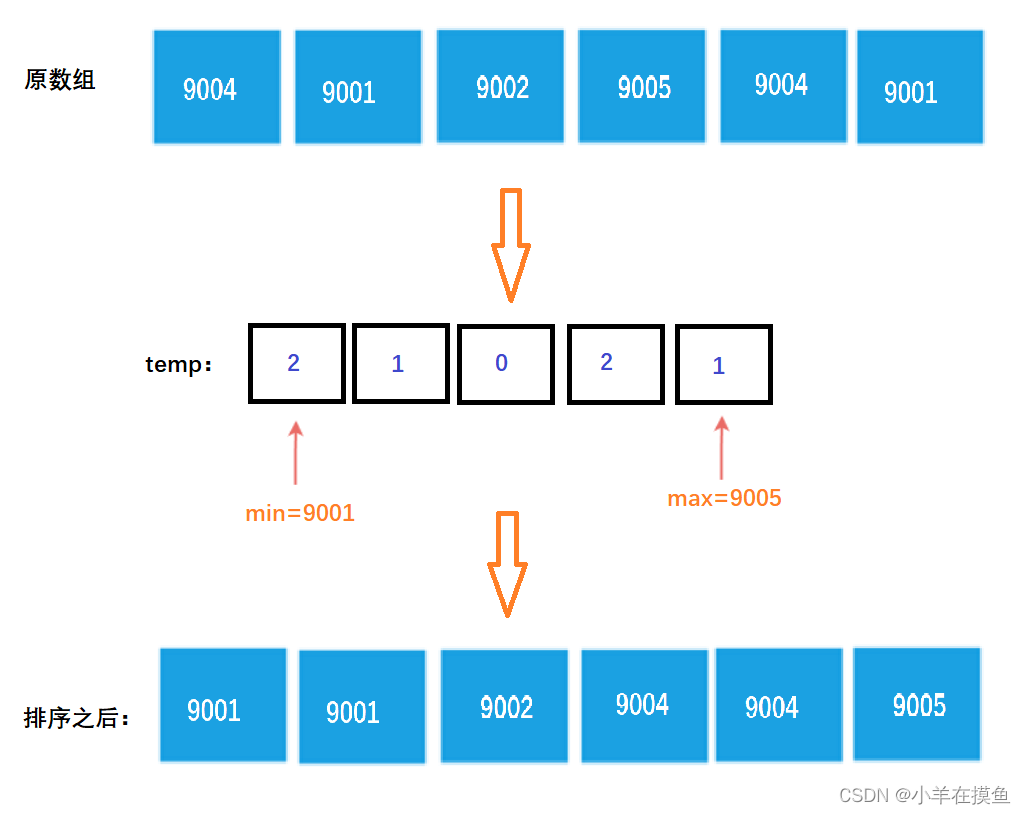
当然,对于负数也一样可以使用,这里就不一一展示了
计算排序的特点:
- 稳定性:稳定
- 时间复杂度:O(n+k)
- 空间复杂度:O(n+k)
对于数据率不是很大,并且数据比较集中时,计数排序是一个很有效的排序算法
计数排序的局限性:
不能对小数进行排序,只适用于整数
代码实现
分4步实现
- 找到数组中的最大最小值
- 计算范围,开辟临时数组空间
- 统计相同元素出现次数
- 根据计数结果将序列依次放回原来的数组中
//计数排序
void CountSort(int* a, int n)
{//确定数组里面的最大最小值int max = a[0], min = a[0];for (int i = 1;i < n;i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}//范围 = 最大值 - 最小值 + 1//比如从 0 到 9 有10个数int range = max - min + 1;//用calloc开辟range个大小为int的空间,并给每个元素赋值为0int* countA = (int*)calloc(range, sizeof(int));if (countA == NULL){perror("calloc fail");exit(-1);}//统计相同元素出现的次数for (int i = 0;i < n;i++){//a[i] - min 是a[i]下标在countA里面对应的相对位置countA[a[i] - min]++;}//排序,根据计数结果将序列依次放回原来的数组中int k = 0;for (int j = 0;j < range;j++){while (countA[j]--){//j + min 就是数组元素的大小a[k++] = j + min;}}free(countA);
}排序算法复杂度及稳定性分析
什么时稳定性?
稳定性的价值:
比如再考试排名的时候,第三名种有三个人的成绩相同,那么如果先交卷的人是第三名的话,就要去再成绩排序的时候保证其稳定性
各种常见排序算法的总结
相关文章:

数据结构_第十三关(3):归并排序、计数排序
目录 归并排序 1.基本思想: 2.原理图: 1)分解合并 2)数组比较和归并方法: 3.代码实现(递归方式): 4.归并排序的非递归方式 原理: 情况1: 情况2&…...

“成功学大师”杨涛鸣被抓
我是卢松松,点点上面的头像,欢迎关注我哦! 4月15日,号称帮助一百多位草根开上劳斯莱斯,“成功学大师”杨涛鸣机其团队30多人已被刑事拘留,培训课程涉嫌精神传销,警方以诈骗案进行立案调查。 …...
【hello C++】内存管理
目录 前言: 1. C/C内存分布 2. C语言动态内存管理方式 3. C内存管理方式 3.1 new / delete 操作内置类型 3.2 new和delete操作自定义类型 4. operator new与operator delete函数 4.1 operator new与operator delete函数 5. new和delete的实现原理 5.1 内置类型 5.2…...
)
AppArmor零知识学习十二、源码构建(9)
本文内容参考: AppArmor / apparmor GitLab 接前一篇文章:AppArmor零知识学习十一、源码构建(8) 在前一篇文章中完成了apparmor源码构建的第六步——Apache mod_apparmor的构建和安装,本文继续往下进行。 四、源码…...

Unity - 带耗时 begin ... end 的耗时统计的Log - TSLog
CSharp Code // jave.lin 2023/04/21 带 timespan 的日志 (不帶 log hierarchy 结构要求,即: 不带 stack 要求)using System; using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEngine;public…...

Python 智能项目:1~5
原文:Intelligent Projects Using Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何实…...

C++设计模式:面试题精选集
目录标题 引言(Introduction)面试的重要性设计模式概述面试题的选择标准 设计模式简介 面试题解析:创建型模式(Creational Patterns Analysis)面试题与解答代码实例应用场景分析 面试题解析:结构型模式&…...

蓝桥 卷“兔”来袭编程竞赛专场-10仿射加密 题解
赛题介绍 挑战介绍 仿射密码结合了移位密码和乘数密码的特点,是一种替换密码。它是利用加密函数一个字母对一个字母的加密。加密函数是 yaxb(mod m) ,且 a,b∈Zm (a、b 的值在 m 范围内),且 a、m 互质。 m 是字符集的…...

android so库导致的闪退及tombstone分析
android中有3种crash情况:未捕获的异常、ANR和闪退。未捕获的异常一般用crash文件就可以记录异常信息,而ANR无响应表现就是界面卡着无法响应用户操作,而闪退则是整个app瞬间退出,个人感觉对用户造成的体验最差。闪退一般是由于调用…...

图结构基本知识
图 1. 相关概念2. 图的表示方式3. 图的遍历3.1 深度优先遍历(DFS)3.2 广度优先遍历(BFS) 1. 相关概念 图G(V,E) :一种数据结构,可表示“多对多”关系,由顶点集V和边集E组成;顶点(ve…...

Hibernate 的多种查询方式
Hibernate 是一个开源的 ORM(对象关系映射)框架,它可以将 Java 对象映射到数据库表中,实现对象与关系数据库的映射。Hibernate 提供了多种查询方式,包括 OID 检索、对象导航检索、HQL 检索、QBC 检索和 SQL 检索。除此…...
FreeRTOS 任务调度及相关函数详解(一)
文章目录 一、任务调度器开启函数 vTaskStartScheduler()二、内核相关硬件初始化函数 xPortStartScheduler()三、启动第一个任务 prvStartFirstTask()四、中断服务函数 xPortPendSVHandler()五、空闲任务 一、任务调度器开启函数 vTaskStartScheduler() 这个函数的功能就是开启…...
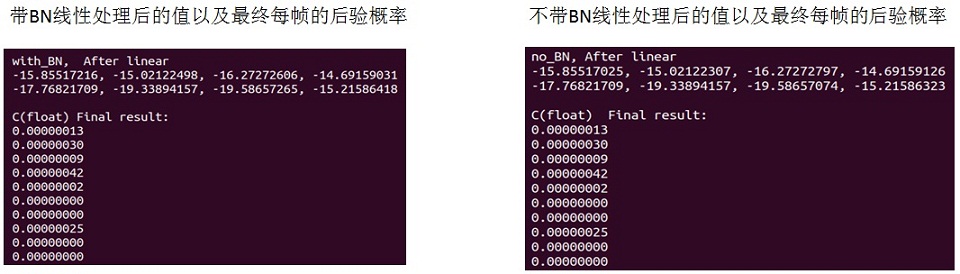
飞桨paddlespeech语音唤醒推理C实现
上篇(飞桨paddlespeech 语音唤醒初探)初探了paddlespeech下的语音唤醒方案,通过调试也搞清楚了里面的细节。因为是python 下的,不能直接部署,要想在嵌入式上部署需要有C下的推理实现,于是我就在C下把这个方…...

04-Mysql常用操作
1. DDL 常见数据库操作 # 查询所有数据库 show databases; # 查询当前数据库 select databases();# 使用数据库 use 数据库名;# 创建数据库 create database [if not exits] 数据库名; # []代表可选可不选# 删除数据库 drop database [if exits] 数据库名; 常见表操作 创建…...

TensorFlow 2 和 Keras 高级深度学习:1~5
原文:Advanced Deep Learning with TensorFlow 2 and Keras 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...
UML类图
一、UML 1、什么是UML? UML——Unified modeling language UML(统一建模语言),是一种用于软件系统分析和设计的语言工具,它用于帮助软件开发人员进行思考和记录思路的结果。UML本身是一套符号的规定,就像数学符号和化学符号一样&…...

【Python】【进阶篇】二十六、Python爬虫的Scrapy爬虫框架
目录 二十六、Python爬虫的Scrapy爬虫框架26.1 Scrapy下载安装26.2 创建Scrapy爬虫项目1) 创建第一个Scrapy爬虫项目 26.3 Scrapy爬虫工作流程26.4 settings配置文件 二十六、Python爬虫的Scrapy爬虫框架 Scrapy 是一个基于 Twisted 实现的异步处理爬虫框架,该框架…...

PyTorch 深度学习实用指南:6~8
原文:PyTorch Deep Learning Hands-On 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何实现目…...

数据湖 Hudi 核心概念
文章目录 什么是 Hudi ?Hudi 是如何对数据进行管理的?Hudi 表结构Hudi 核心概念 什么是 Hudi ? Hudi 是一个用于处理大数据湖的开源框架。 大数据湖是指一个大规模的、中心化的数据存储库,其中包含各种类型的数据,如结构化数据、半结构化…...

爬虫请求头Content-Length的计算方法
重点:使用node.js 环境计算,同时要让计算的数据通过JSON.stringify从对象变成string。 1. Blob size var str 中国 new Blob([str]).size // 6 2、Buffer.byteLength # node > var str 中国 undefined > Buffer.byteLength(str, utf8) 6 原文…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...