图结构基本知识
图
- 1. 相关概念
- 2. 图的表示方式
- 3. 图的遍历
- 3.1 深度优先遍历(DFS)
- 3.2 广度优先遍历(BFS)
1. 相关概念
- 图G(V,E) :一种数据结构,可表示“多对多”关系,由顶点集V和边集E组成;
- 顶点(vertex) :
- 边 (edge):一幅点对(v,w),v,w∈V,边也称为弧;
- 邻接:点v,w邻接,当且仅当边(v,w)∈E;
- 路径 :由一个顶点序列v1,v2,…,vn组成,路径长为n-1;
- 有向图 :边是单向的,点对有序;
- 无向图 :边是双向的图,点对无序;
- 带权图:不同边具有不同的权值的图;
- 连通:无向图的一个顶点到其他任何顶点都存在一条路径,则称其为连通的;
- 强连通:有向图的一个顶点到其他任何顶点都存在一条路径;
- 弱连通:有向图本身不是强连通的,但是其边不考虑方向的无向图是连通的;
- 完全图:每一对顶点间都存在边;
2. 图的表示方式
- 邻接矩阵:使用二维数组实现,数组中每个元素表示图中两顶点之间是否有边,或者表示边的权值,适用于稠密图,对于稀疏图而言此表示方法过于浪费空间;

package com.northsmile.graph;import java.util.ArrayList;
import java.util.Arrays;/*** Author:NorthSmile* Create:2023/4/18 9:17* 使用邻接矩阵表示图(无向图)*/
public class Graph {// 存储边及其权值int[][] edges;// 存储顶点ArrayList<String> vertexes;// 记录边的数目int edgeNums;public Graph(int n){edges=new int[n][n];vertexes=new ArrayList<>(n);edgeNums=0;}/*** 插入顶点* @param vertex*/public void insertVertex(String vertex){vertexes.add(vertex);}/*** 插入边* @param v1 边的一个顶点对应下标* @param v2 边的另一个顶点对应下标* @param w 边对应权值,默认为1*/public void insertEdge(int v1,int v2,int w){edges[v1][v2]=w;edges[v2][v1]=w;edgeNums++;}/*** 获取顶点数量* @return*/public int getVertexesNum(){return vertexes.size();}/*** 获取边的数目* @return*/public int getEdgesNum(){return edgeNums;}/*** 获取指定下标对应的顶点的值* @param v* @return*/public String getValByIndex(int v){return vertexes.get(v);}/*** 获取指定边的权值* @param v1* @param v2* @return*/public int getWeightOfEdge(int v1,int v2){return edges[v1][v2];}/*** 显示表示图的邻接矩阵*/public void showGraph(){for (int[] edge:edges){System.out.println(Arrays.toString(edge));}}
}package com.northsmile.graph;/*** Author:NorthSmile* Create:2023/4/18 9:18*/
public class GraphDemo {public static void main(String[] args) {int n=5;String[] vertexes={"A","B","C","D","E"};Graph graph = new Graph(n);// 插入顶点for (String vertex:vertexes){graph.insertVertex(vertex);}// 插入边graph.insertEdge(0,1,1);graph.insertEdge(0,2,1);graph.insertEdge(1,2,1);graph.insertEdge(1,3,1);graph.insertEdge(1,4,1);graph.showGraph();}
}
- 邻接表:使用数组+链表的方式实现,适用于稀疏图表示,是图的标准表示方法,对于每个顶点,将其所有邻接点使用一个表存放;

package com.northsmile.graph;import java.util.ArrayList;
import java.util.HashMap;/*** Author:NorthSmile* Create:2023/4/18 11:12* 使用邻接表表示图(有向图)*/
public class GraphByAdjacenceList {// 邻接表HashMap<String,Vertex> list;int vertexNums;int edgeNums;public GraphByAdjacenceList(int n){list=new HashMap<>();vertexNums=n;edgeNums=0;}/*** 插入顶点* @param vertex*/public void insertVertex(String vertex){list.put(vertex,new Vertex(vertexNums));}/*** 插入边* @param v 顶点* @param w 邻接点*/public void insertEdge(String v,String w){Vertex vertex = list.get(v);vertex.table.add(w);edgeNums++;}/*** 获取顶点数量* @return*/public int getVertexesNum(){return list.size();}/*** 获取边的数目* @return*/public int getEdgesNum(){return edgeNums;}/*** 显示表示图的邻接表*/public void showGraph(){for (String vertex:list.keySet()){System.out.println(vertex+":"+list.get(vertex).table);}}/*** 顶点类*/class Vertex{ArrayList<String> table;public Vertex(int n){table=new ArrayList<>(n/2);}}
}package com.northsmile.graph;/*** Author:NorthSmile* Create:2023/4/18 9:18*/
public class GraphDemo {public static void main(String[] args) {// 2.邻接表int n=5;String[] vertexes={"A","B","C","D","E"};GraphByAdjacenceList graph = new GraphByAdjacenceList(n);// 插入顶点for (String vertex:vertexes){graph.insertVertex(vertex);}// 插入边graph.insertEdge("A","B");graph.insertEdge("A","C");graph.insertEdge("B","C");graph.insertEdge("B","D");graph.insertEdge("B","E");graph.showGraph();}
}
3. 图的遍历

3.1 深度优先遍历(DFS)
- 类似树的先序遍历,先访问当前顶点,再依次以其邻接点为新的起点,进行深度优先遍历;
- 与树的遍历不同,图在深度优先遍历时,当前顶点的邻接点可能已经访问过,所以无需再进行访问;
- 为了实现顶点的唯一遍历,在代码实现时需要提供一个标记数组,表示对应顶点是否已经访问过;
- 代码实现以递归方式进行;


/*** 深度优先遍历:类似树的先序遍历* @param v 以当前点开始遍历* @param visited 标记节点是否访问过*/public void dfs(int v,boolean[] visited){System.out.print(vertexes.get(v)+"->");// 遍历当前顶点的邻接点for (int i=0;i<vertexes.size();i++){// 说明v、i之间存在边if (edges[v][i]!=0&&!visited[i]){visited[i]=true;dfs(i,visited);}}}public void dfs(){// 标记顶点是否已经访问过boolean[] visited=new boolean[vertexes.size()];// 以每个顶点开始进行DFS,实现图的完整遍历for (int i=0;i<vertexes.size();i++){if (!visited[i]){visited[i]=true;dfs(i,visited);}}}
3.2 广度优先遍历(BFS)
- 类似树的层序遍历,先访问当前顶点,再依次访问其邻接点,然后分别以其邻接点为新的起点,继续进行广度优先遍历;
- 与树的遍历不同,图在深度优先遍历时,当前顶点的邻接点可能已经访问过,所以无需再进行访问;
- 为了实现顶点的唯一遍历,在代码实现时需要提供一个标记数组,表示对应顶点是否已经访问过;
- 代码实现借助队列实现;

/*** 广度优先遍历:类似树的层次遍历* @param v 以当前点开始遍历* @param visited 标记节点是否访问过*/public void bfs(int v,boolean[] visited){ArrayDeque<Integer> queue=new ArrayDeque<>();queue.offer(v);visited[v]=true;while (!queue.isEmpty()){Integer cur = queue.poll();System.out.print(vertexes.get(cur)+"->");// 遍历当前顶点的邻接点for (int i=0;i<vertexes.size();i++){// 说明v、i之间存在边if (edges[cur][i]!=0&&!visited[i]){visited[i]=true;queue.offer(i);}}}}public void bfs(){// 标记顶点是否已经访问过boolean[] visited=new boolean[vertexes.size()];// 以每个顶点开始进行BFS,实现图的完整遍历for (int i=0;i<vertexes.size();i++){if (!visited[i]){bfs(i,visited);}}}
资料来源:尚硅谷
相关文章:

图结构基本知识
图 1. 相关概念2. 图的表示方式3. 图的遍历3.1 深度优先遍历(DFS)3.2 广度优先遍历(BFS) 1. 相关概念 图G(V,E) :一种数据结构,可表示“多对多”关系,由顶点集V和边集E组成;顶点(ve…...

Hibernate 的多种查询方式
Hibernate 是一个开源的 ORM(对象关系映射)框架,它可以将 Java 对象映射到数据库表中,实现对象与关系数据库的映射。Hibernate 提供了多种查询方式,包括 OID 检索、对象导航检索、HQL 检索、QBC 检索和 SQL 检索。除此…...
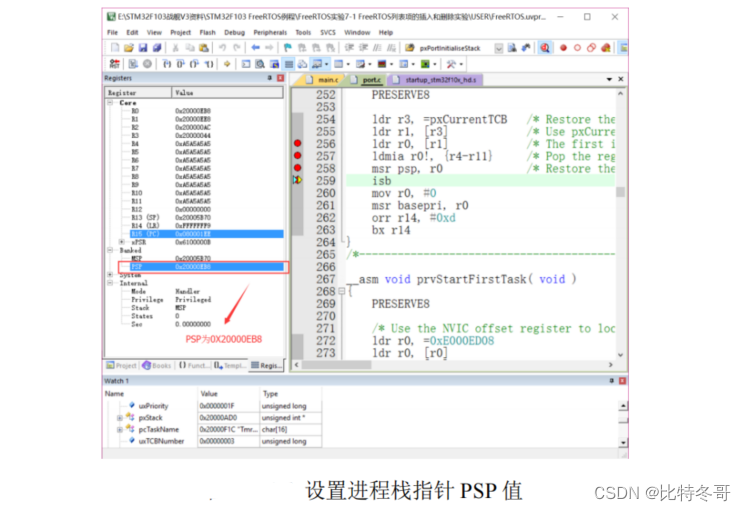
FreeRTOS 任务调度及相关函数详解(一)
文章目录 一、任务调度器开启函数 vTaskStartScheduler()二、内核相关硬件初始化函数 xPortStartScheduler()三、启动第一个任务 prvStartFirstTask()四、中断服务函数 xPortPendSVHandler()五、空闲任务 一、任务调度器开启函数 vTaskStartScheduler() 这个函数的功能就是开启…...
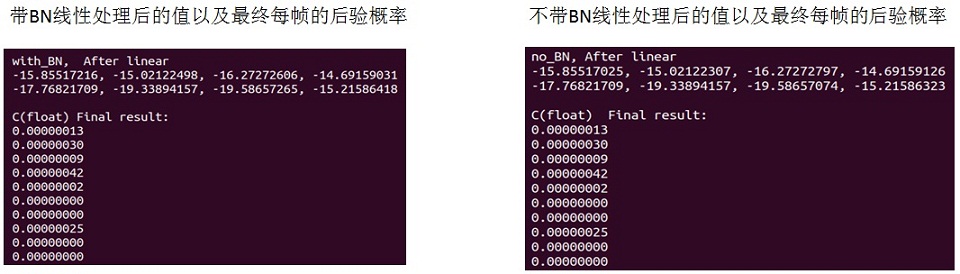
飞桨paddlespeech语音唤醒推理C实现
上篇(飞桨paddlespeech 语音唤醒初探)初探了paddlespeech下的语音唤醒方案,通过调试也搞清楚了里面的细节。因为是python 下的,不能直接部署,要想在嵌入式上部署需要有C下的推理实现,于是我就在C下把这个方…...

04-Mysql常用操作
1. DDL 常见数据库操作 # 查询所有数据库 show databases; # 查询当前数据库 select databases();# 使用数据库 use 数据库名;# 创建数据库 create database [if not exits] 数据库名; # []代表可选可不选# 删除数据库 drop database [if exits] 数据库名; 常见表操作 创建…...

TensorFlow 2 和 Keras 高级深度学习:1~5
原文:Advanced Deep Learning with TensorFlow 2 and Keras 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象&#x…...
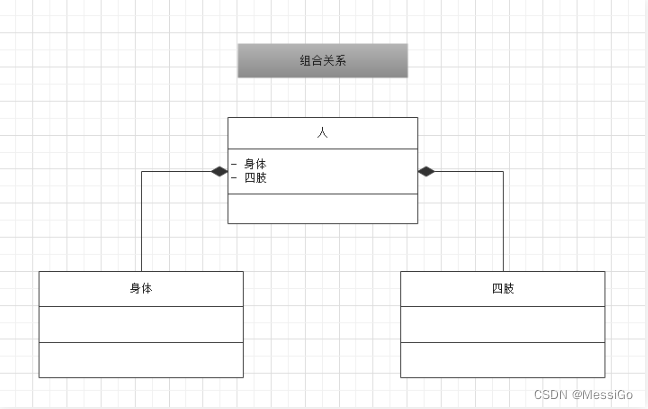
UML类图
一、UML 1、什么是UML? UML——Unified modeling language UML(统一建模语言),是一种用于软件系统分析和设计的语言工具,它用于帮助软件开发人员进行思考和记录思路的结果。UML本身是一套符号的规定,就像数学符号和化学符号一样&…...

【Python】【进阶篇】二十六、Python爬虫的Scrapy爬虫框架
目录 二十六、Python爬虫的Scrapy爬虫框架26.1 Scrapy下载安装26.2 创建Scrapy爬虫项目1) 创建第一个Scrapy爬虫项目 26.3 Scrapy爬虫工作流程26.4 settings配置文件 二十六、Python爬虫的Scrapy爬虫框架 Scrapy 是一个基于 Twisted 实现的异步处理爬虫框架,该框架…...

PyTorch 深度学习实用指南:6~8
原文:PyTorch Deep Learning Hands-On 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 不要担心自己的形象,只关心如何实现目…...

数据湖 Hudi 核心概念
文章目录 什么是 Hudi ?Hudi 是如何对数据进行管理的?Hudi 表结构Hudi 核心概念 什么是 Hudi ? Hudi 是一个用于处理大数据湖的开源框架。 大数据湖是指一个大规模的、中心化的数据存储库,其中包含各种类型的数据,如结构化数据、半结构化…...

爬虫请求头Content-Length的计算方法
重点:使用node.js 环境计算,同时要让计算的数据通过JSON.stringify从对象变成string。 1. Blob size var str 中国 new Blob([str]).size // 6 2、Buffer.byteLength # node > var str 中国 undefined > Buffer.byteLength(str, utf8) 6 原文…...
Open Inventor 2023.1 Crack
发行说明 Open Inventor 2023.1(次要版本) 文档于 2023 年 4 月发布。 此版本中包含的增强功能和新功能: Open Inventor 10 版本编号更改体积可视化 单一分辨率的体绘制着色器中与裁剪和 ROI 相关的新功能MeshVizXLM 在 C 中扩展的剪辑线提…...
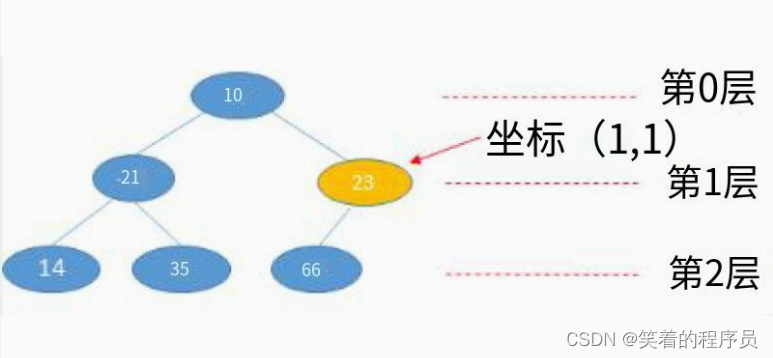
【华为OD机试真题】查找树中元素(查找二叉树节点)(javaC++python)100%通过率
查找树中元素 知识点树BFSQ搜索广搜 时间限制:1s空间限制:256MB限定语言:不限 题目描述: 已知树形结构的所有节点信息,现要求根据输入坐标(x,y)找到该节点保存的内容 值;其中: x表示节点所在的层数,根节点位于第0层,根节点的子节点位于第1层,依次类推; y表示节…...

常用设计模式
里氏替换原则:子类可以扩展父类的功能,但是不要更改父类的已经实现的方法子类对父类的方法尽量不要重写和重载。(我们可以采用final的手段强制来遵循)创建型模式 单例模式:维护线程数据安全 懒汉式 public class Test{ 饿汉式 private static final Test…...
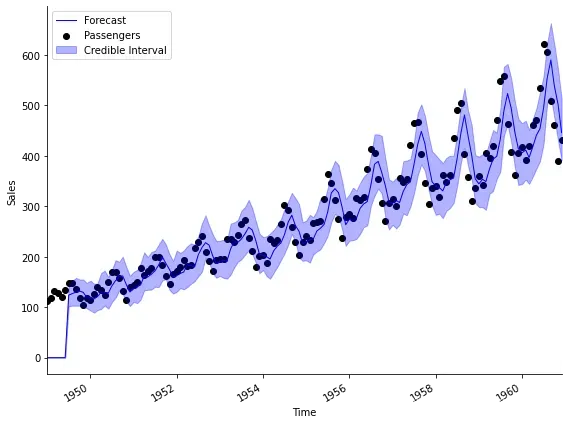
时序分析 49 -- 贝叶斯时序预测(一)
贝叶斯时序预测(一) 时序预测在统计分析和机器学习领域一直都是一个比较重要的话题。在本系列前面的文章中我们介绍了诸如ARIMA系列方法,Holt-Winter指数平滑模型等多种常用方法,实际上这些看似不同的模型和方法之间都具有千丝万缕…...

从传统管理到智慧水务:数字化转型的挑战与机遇
概念 智慧水务是指利用互联网、物联网、大数据、人工智能等技术手段,将智能化、信息化、互联网等技术与水务领域相结合,通过感知、传输、处理水质、水量、水价等数据信息,对水资源进行全面监测、综合管理、智能调度和优化配置的智能化水务系…...
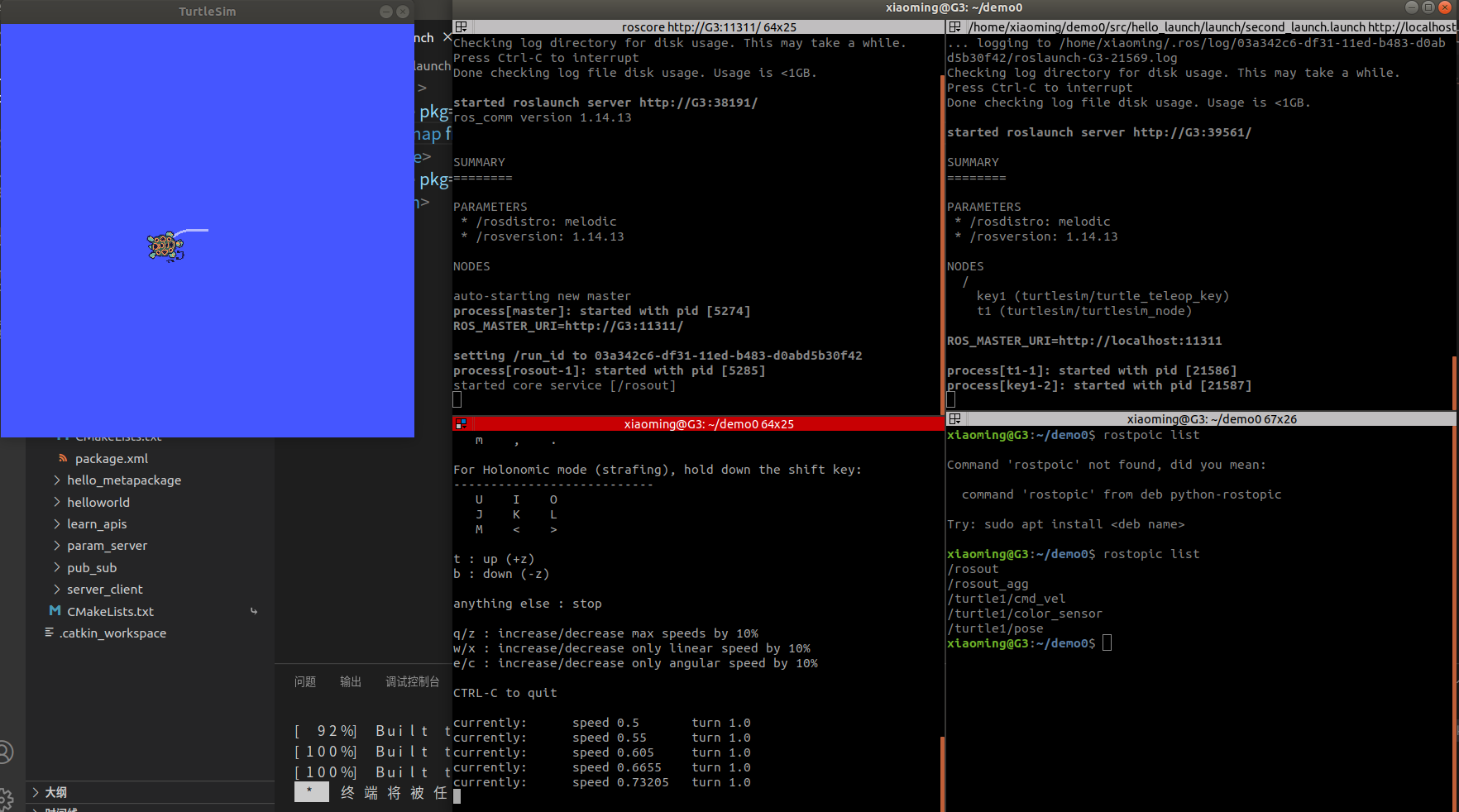
ROS学习第十八节——launch文件(详细介绍)
1.概述 关于 launch 文件的使用已经不陌生了,之前就曾经介绍到: 一个程序中可能需要启动多个节点,比如:ROS 内置的小乌龟案例,如果要控制乌龟运动,要启动多个窗口,分别启动 roscore、乌龟界面节点、键盘控制节点。如果…...
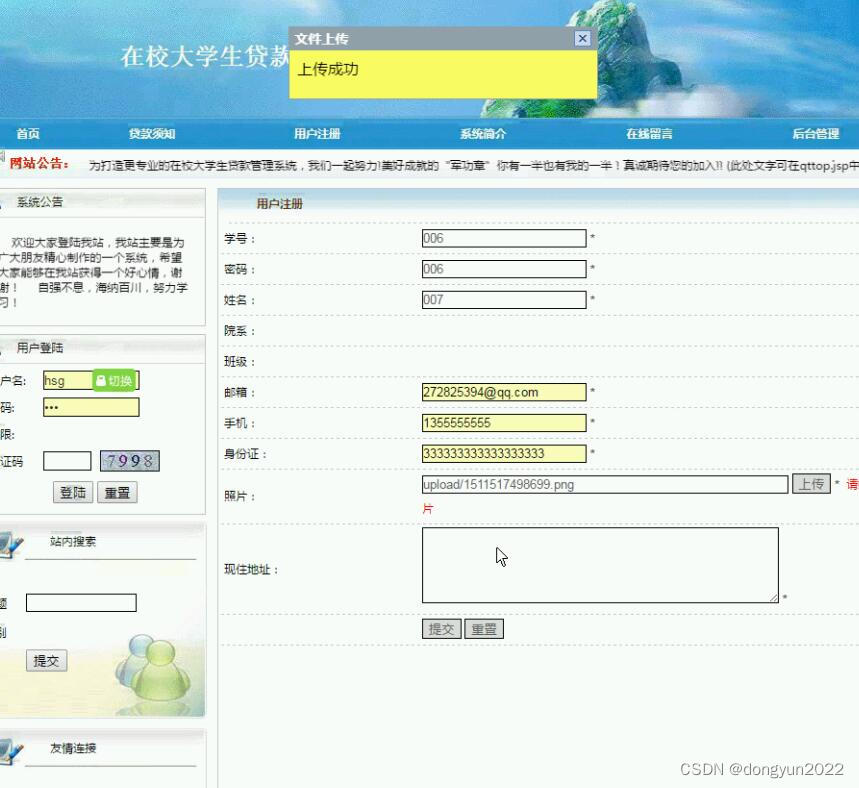
javaweb在校大学生贷款管理系统ns08a9
1系统主要实现:学生注册、填写详细资料、申请贷款、学校审核、银行审核、贷后管理等功能, (1) 学生注册:学生通过注册用户,提交自己的详细个人资料,考虑现实应用中的安全性,资料提交后不可修改;…...
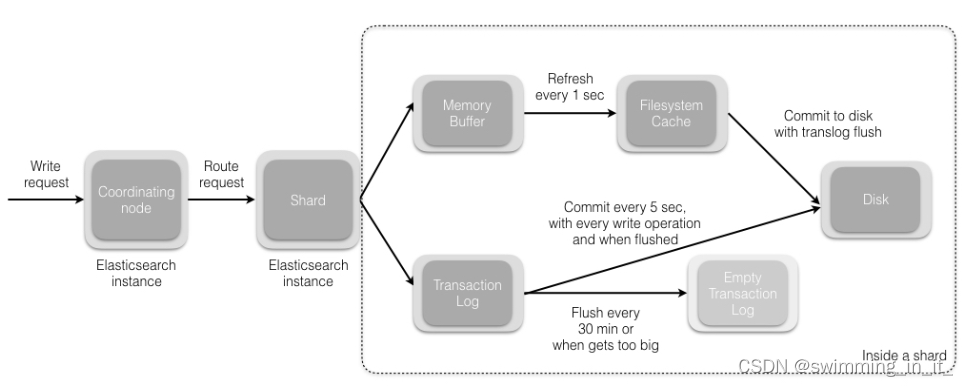
分布式之搜索解决方案es
一 ES初识 1.1 概述 ElasticSearch:是基于 Lucene 的 Restful 的分布式实时全文搜索引擎,每个字段都被索引并可被搜索,可以快速存储、搜索、分析海量的数据。是ELK的一个组成,是一个产品,而且是非常完善的产品,ELK代表…...

CSDN 编程竞赛四十六期题解
地址:CSDN 编程竞赛四十六期 思路:通过找规律可以知道,在周期第一个位置的数的下标都有一个规律:除以三的余数为 1 。而第二个位置,第三个位置的余数分别为 2 , 0 。 因此可以开一个长度为 3 的总和数组&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
