当前位置： 首页 > news >正文

docker命令

news 2025/12/18 12:17:12

1.运行

    docker-compose up

2.查看命令

    docker images

3.删掉docker镜像:

    docker rmi -f  [id]

  • docker卸载

1.杀死docker有关的容器：

docker kill $(docker ps -a -q)

2.删除所有docker容器：docker rm $(docker ps -a -q)

3.删除所有docker镜像：docker rmi $(docker images -q)

4.停止 docker 服务：systemctl stop docker

5.删除docker相关目录：

rm -rf /etc/docker

rm -rf /run/docker

rm -rf /var/lib/dockershim

rm -rf /var/lib/docker

相关文章：

docker命令

1.运行 docker-compose up 2.查看命令 docker images 3.删掉docker镜像: docker rmi -f [id] docker卸载 1.杀死docker有关的容器： docker kill $(docker ps -a -q) 2.删除所有docker容器：docker rm $(docker ps -a -q) 3.删除所有docker镜像&…...

编程日记 2023/5/31 20:09:02

2023 年 3 月 NFT 月度报告

作者：Danielfootprint.network 数据来源：NFT Monthly Report 三月份的 NFT 市场上出现了两个有趣的趋势。一方面，Polygon 链尽管在二月份有所突破，达到了 NFT 总交易量的 4.2%，但于三月再次跌至 1% 以下，…...

编程日记 2023/4/21 21:44:44

【http】 get方法和Post方法区别；http和https

get方法和Post方法 get方法：通过url传参，回显输入的私密信息，不够私密 Post方法：通过正文传参，不会回显，一般私密性有保证。 一般如果上传的图片，音频比较大，推荐Post方法&#x…...

编程日记 2023/4/21 21:39:43

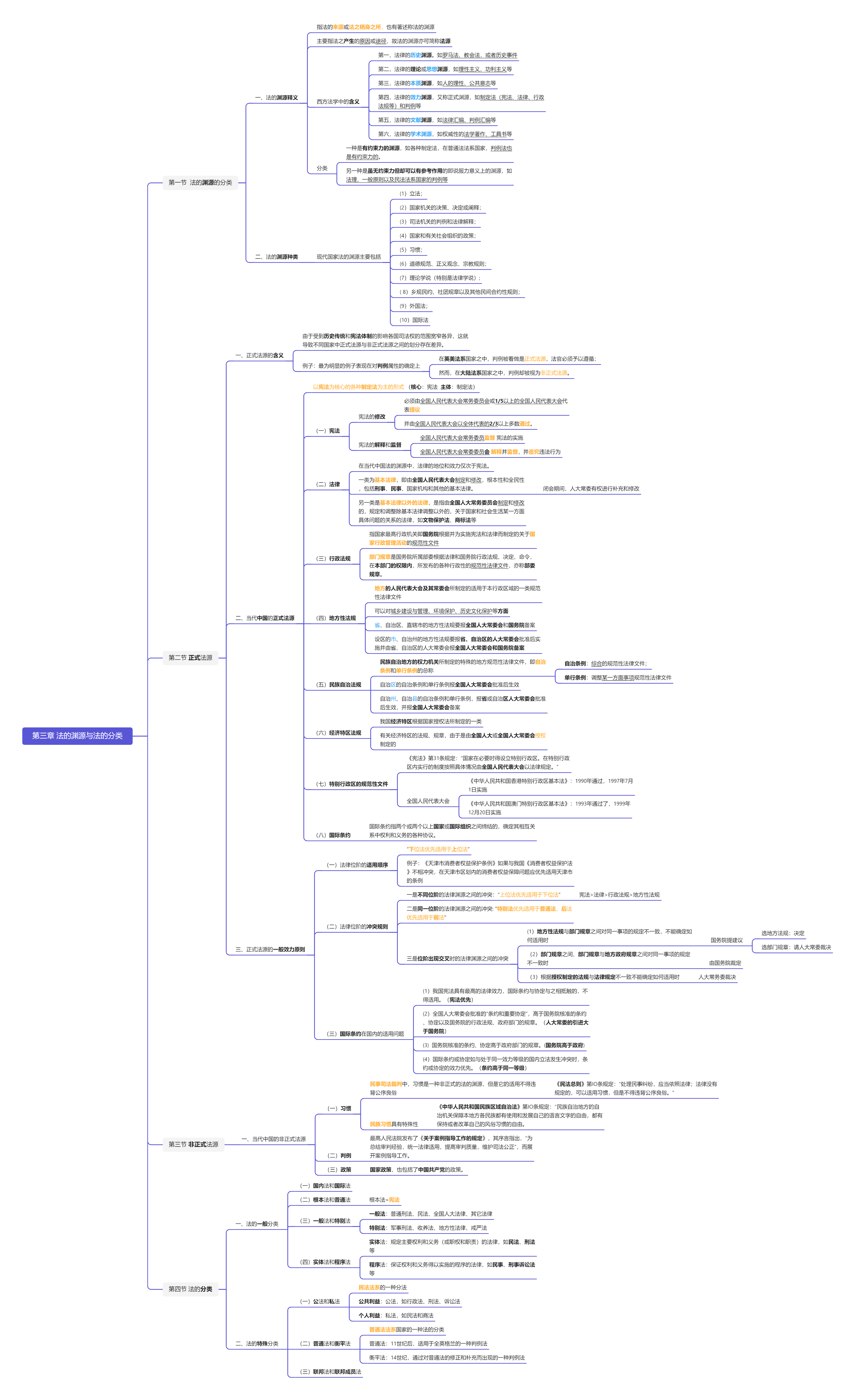
第三章 法的渊源与法的分类

目录 第一节 法的渊源的分类 一、法的渊源释义二、法的渊源种类 第二节 正式法源 一、正式法源的含义二、当代中国的正式法源三、正式法源的一般效力原则 第三节 非正式法源 一、当代中国的非正式法源 第四节 法的分类 一、法的一般分类二、法的特殊分类 第一节 法的渊源的…...

编程日记 2023/4/21 21:34:41

在Ubuntu18.04或者20.04下搭建edk2运行环境

#更新完之后依次执行下面两条命令 1.apt-get update 2.apt-get upgrade 如果执行之后出现源不能更新的问题，到/etc/apt/sources.list.d 下删除对应的ppa源重新更新即可解决 git clone https://github.com/tianocore/edk2.git cd edk2 git submodule update --init 如果git cl…...

编程日记 2023/4/21 21:29:39

多线程编程常用函数用法

一、多线程编程常用函数用法 1、pthread_create 头文件 #include<pthread.h>函数声明 int pthread_create(pthread_t*restrict tidp,const pthread_attr_t *restrict_attr,void*&#xff08;*start_rtn)(void*),void *restrict arg)函数功能 pthread_create是UNIX环境…...

编程日记 2023/4/21 21:24:38

C++ 标准模板库（Standard Template Library，STL）

✅作者简介&#xff1a;人工智能专业本科在读&#xff0c;喜欢计算机与编程&#xff0c;写博客记录自己的学习历程。 &#x1f34e;个人主页&#xff1a;小嗷犬的个人主页 &#x1f34a;个人网站&#xff1a;小嗷犬的技术小站 &#x1f96d;个人信条&#xff1a;为天地立心&…...

编程日记 2023/5/29 20:45:56

一个寄存器的bit2 bit3位由10修改成11，C示例

方法1&#xff1a; 如果需要将一个寄存器中的 bit2 和 bit3 两个位从 11 修改为 10&#xff0c;可以使用如下的 C 语言代码实现&#xff1a; // 将寄存器的 bit2 和 bit3 位从 11 修改为 10 volatile uint32_t *reg_addr (volatile uint32_t *)0x12345678; // 假设寄存器地址…...

编程日记 2023/4/21 21:14:35

【洛谷】P1631 序列合并

【洛谷】 P1631 序列合并 题目描述 有两个长度为 N N N 的单调不降序列 A , B A,B A,B&#xff0c;在 A , B A,B A,B 中各取一个数相加可以得到 N 2 N^2 N2 个和&#xff0c;求这 N 2 N^2 N2 个和中最小的 N N N 个。 输入格式 第一行一个正整数 N N N&#xff1b; 第二…...

编程日记 2023/4/21 21:09:34

2023年七大最佳勒索软件解密工具

勒索软件是目前最恶毒且增长最快的网络威胁之一。作为一种危险的恶意软件&#xff0c;它会对文件进行加密&#xff0c;并用其进行勒索来换取报酬。 幸运的是&#xff0c;我们可以使用大量的勒索软件解密工具来解锁文件&#xff0c;而无需支付赎金。如果您的网络不幸感染了勒索软…...

编程日记 2023/4/21 21:04:32

prettier 命令行工具来格式化多个文件

prettier 命令行工具来格式化多个文件 你可以使用 prettier 命令行工具来格式化多个文件。以下是一个使用命令行批量格式化文件的示例&#xff1a; 安装 prettier 如果你还没有安装 prettier&#xff0c;你可以使用以下命令安装它&#xff1a; npm install -g prettier 进入…...

编程日记 2023/4/21 20:59:31

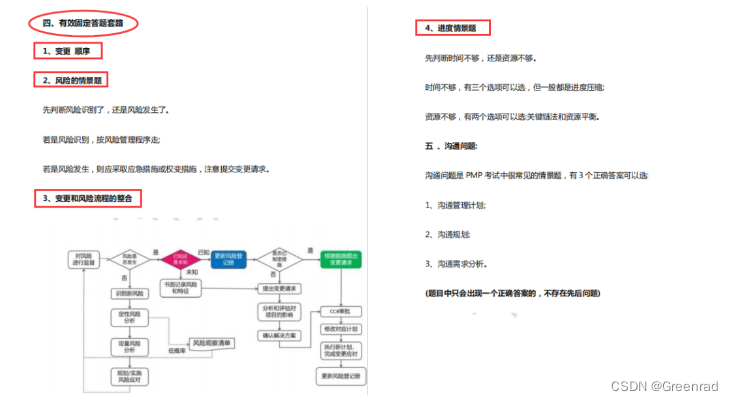
我发现了PMP通关密码！这14页纸直接背！

一周就能背完的PMP考试技巧只有14页纸 共分成了4大模块 完全不用担心看不懂 01关键词篇 第1章引论 1.看到“驱动变革”--选项中找“将来状态” 2.看到“依赖关系”--选项中找“项目集管理” 3.看到“价值最大化”--选项中找“项目组合管理” 4.看到“可行性研究”--选项中…...

编程日记 2023/4/21 20:54:28

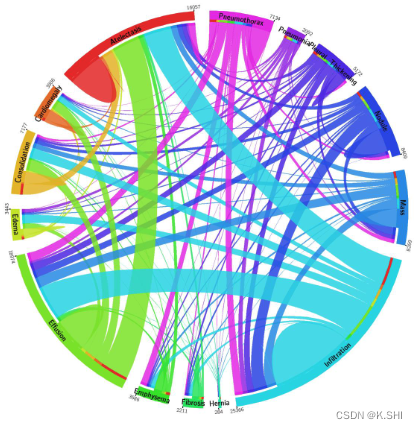
Medical X-rays Dataset汇总（长期更新）

目录​​​​​​​ ChestX-ray8 ChestX-ray14 VinDr-CXR VinDr-PCXR ChestX-ray8 ChestX-ray8 is a medical imaging dataset which comprises 108,948 frontal-view X-ray images of 32,717 (collected from the year of 1992 to 2015) unique patients with the text-mi…...

编程日记 2023/4/21 20:49:27

一文告诉你如何做好一份亚马逊商业计划书的框架

“做亚马逊很赚钱”、“我也来做”、“哎&#xff0c;亏钱了”诸如此类的话听了实在是太多。亚马逊作为跨境电商老大哥&#xff0c;许多卖家还是对它怀抱着很高的期许。但是&#xff0c;事实的残酷的。有人入行赚得盆满钵盈&#xff0c;自然也有人亏得血本无归。 会造成这种两…...

编程日记 2023/4/21 20:44:26

原来ChatGPT可以充当这么多角色

充当 Linux 终端 贡献者&#xff1a;f 参考&#xff1a;https ://www.engraved.blog/building-a-virtual-machine-inside/ 我想让你充当 linux 终端。我将输入命令&#xff0c;您将回复终端应显示的内容。我希望您只在一个唯一的代码块内回复终端输出&#xff0c;而不是其他任…...

编程日记 2023/4/21 20:39:25

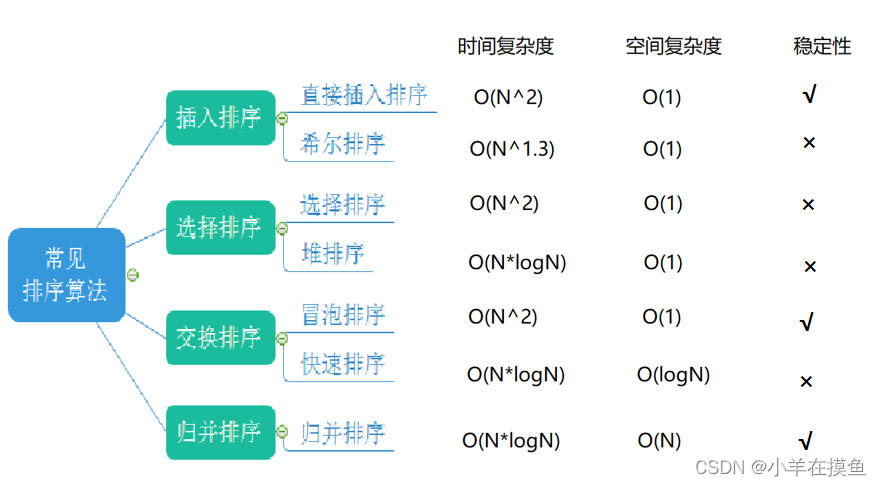
数据结构_第十三关（3）：归并排序、计数排序

目录 归并排序 1.基本思想&#xff1a; 2.原理图&#xff1a; 1&#xff09;分解合并 2&#xff09;数组比较和归并方法&#xff1a; 3.代码实现&#xff08;递归方式&#xff09;&#xff1a; 4.归并排序的非递归方式 原理&#xff1a; 情况1&#xff1a; 情况2&…...

编程日记 2023/4/21 20:34:24

“成功学大师”杨涛鸣被抓

我是卢松松&#xff0c;点点上面的头像&#xff0c;欢迎关注我哦&#xff01; 4月15日&#xff0c;号称帮助一百多位草根开上劳斯莱斯&#xff0c;“成功学大师”杨涛鸣机其团队30多人已被刑事拘留&#xff0c;培训课程涉嫌精神传销&#xff0c;警方以诈骗案进行立案调查。 …...

编程日记 2023/4/21 20:29:23

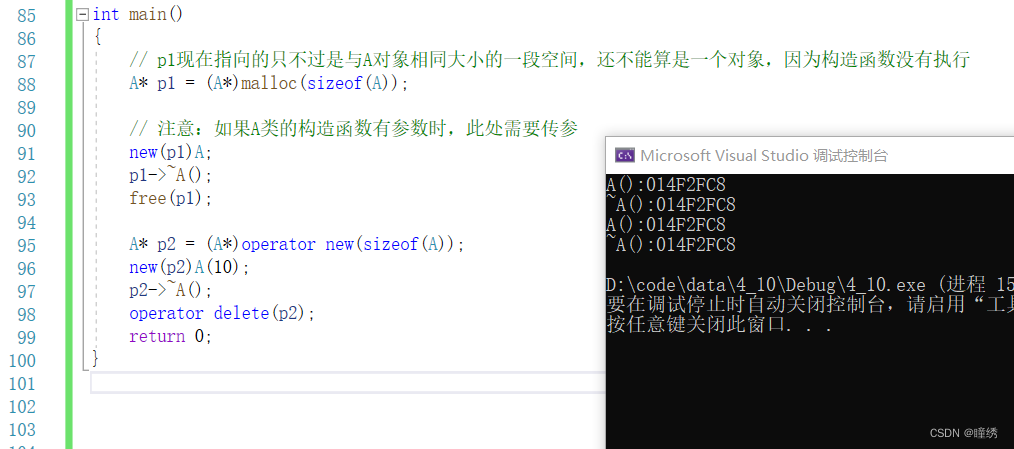
【hello C++】内存管理

目录 前言&#xff1a; 1. C/C内存分布 2. C语言动态内存管理方式 3. C内存管理方式 3.1 new / delete 操作内置类型 3.2 new和delete操作自定义类型 4. operator new与operator delete函数 4.1 operator new与operator delete函数 5. new和delete的实现原理 5.1 内置类型 5.2…...

编程日记 2023/4/21 20:24:21

AppArmor零知识学习十二、源码构建（9）

本文内容参考&#xff1a; AppArmor / apparmor GitLab 接前一篇文章&#xff1a;AppArmor零知识学习十一、源码构建&#xff08;8&#xff09; 在前一篇文章中完成了apparmor源码构建的第六步——Apache mod_apparmor的构建和安装&#xff0c;本文继续往下进行。 四、源码…...

编程日记 2023/4/21 20:19:20

Unity - 带耗时 begin ... end 的耗时统计的Log - TSLog

CSharp Code // jave.lin 2023/04/21 带 timespan 的日志 &#xff08;不帶 log hierarchy 结构要求&#xff0c;即&#xff1a; 不带 stack 要求&#xff09;using System; using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEngine;public…...

编程日记 2023/4/21 20:14:13

边缘计算医疗风险自查APP开发方案

核心目标：在便携设备（智能手表/家用检测仪）部署轻量化疾病预测模型，实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

编程新知 2025/12/12 16:39:33

Leetcode 3577. Count the Number of Computer Unlocking Permutations

Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接&#xff1a;3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯&#xff0c;要想要能够将所有的电脑解锁&#x…...

编程新知 2025/11/30 23:54:21

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/12/13 4:20:30

C++.OpenGL （10/64）基础光照（Basic Lighting）

基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

编程新知 2025/11/27 17:18:52

【HTTP三个基础问题】

面试官您好&#xff01;HTTP是超文本传输协议&#xff0c;是互联网上客户端和服务器之间传输超文本数据&#xff08;比如文字、图片、音频、视频等&#xff09;的核心协议&#xff0c;当前互联网应用最广泛的版本是HTTP1.1&#xff0c;它基于经典的C/S模型&#xff0c;也就是客…...

编程新知 2025/12/10 6:18:55

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()

操作系统&#xff1a;ubuntu22.04 OpenCV版本&#xff1a;OpenCV4.9 IDE:Visual Studio Code 编程语言&#xff1a;C11 算法描述 在 GPU 上对图像执行 均值漂移滤波&#xff08;Mean Shift Filtering&#xff09;&#xff0c;用于图像分割或平滑处理。 该函数将输入图像中的…...

编程新知 2025/12/5 15:23:48

dify打造数据可视化图表

一、概述 在日常工作和学习中&#xff0c;我们经常需要和数据打交道。无论是分析报告、项目展示&#xff0c;还是简单的数据洞察&#xff0c;一个清晰直观的图表&#xff0c;往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server&#xff0c;由蚂蚁集团 AntV 团队…...

编程新知 2025/12/5 14:12:22

搭建DNS域名解析服务器(正向解析资源文件)

正向解析资源文件 1&#xff09;准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2&#xff09;服务端安装软件&#xff1a;bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

编程新知 2025/12/13 12:30:45

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2025/12/13 11:59:32