扩散模型原理记录
1 扩散模型原理记录
参考资料:
[1]【54、Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读】 https://www.bilibili.com/video/BV1b541197HX/?share_source=copy_web&vd_source=7771b17ae75bc5131361e81a50a0c871
[2] https://t.bilibili.com/700526762586538024?spm_id_from=333.999.0.0
以下内容为对上述资料的补充理解,理解不对的地方,请多指教。
以下序号与资料中的章节序号一致。
七、目标数据分布的似然函数
扩散模型本质为生成模型,所以最本质的目标是最大化对数据分布真值的预测概率。
这里可以假设成一个分类问题,不同的类别表示不同的数据分布,其中包括与数据分布真值相近的和不相近的。模型会预测不同数据分布的概率。我们的目标是,使网络对数据分布真值对应的类别的预测概率最高。
用公式表示: m a x p θ ( x 0 ) max~p_{\theta}(x_0) max pθ(x0),其中, p θ ( x 0 ) p_{\theta}(x_0) pθ(x0)为模型对数据分布真值预测的概率分布(注意模型不只是网络,在扩散模型里,网络是模型的一部分,模型还包括对网络输出结果的后处理,因此网络输出值可能多种多样)。
但是 p θ ( x 0 ) p_{\theta}(x_0) pθ(x0)范围是 0 − 1 0-1 0−1,直接最大化不好计算,因此一般转化为最小化对数似然函数: − l o g p θ ( x 0 ) -log~p_{\theta}(x_0) −log pθ(x0)。直接最小化 − l o g p θ ( x 0 ) -log~p_{\theta}(x_0) −log pθ(x0)也不好求,所以扩散模型转而最小化 − l o g p θ ( x 0 ) -log~p_{\theta}(x_0) −log pθ(x0)的上界,这个上界就是 L V L B L_{VLB} LVLB(需要乘 q ( x 0 ) q(x_0) q(x0))。
下面的目标就是最小化 L V L B L_{VLB} LVLB。
L V L B L_{VLB} LVLB最终转化为 L V L B = E q [ L T + L t − 1 ] L_{VLB}=E_q[L_T+L_{t-1}] LVLB=Eq[LT+Lt−1]( L 0 L_0 L0与 L t − 1 L_{t-1} Lt−1合并到一起了),其中, L T L_T LT和 L t − 1 L_{t-1} Lt−1都是两个高斯分布的KL散度,结果只与两个高斯分布的均值和方差有关。 L T L_T LT中两个分布的均值和方差都是已知(在 x 0 x_0 x0分布已知的情况下已知)且不可优化的,因此直接去除。下面计算 L t − 1 L_{t-1} Lt−1,如下式(方差是设定的固定值,所以省略了):

其中, μ ~ ( x t , x 0 ) \tilde\mu(x_t, x_0) μ~(xt,x0)是 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0)高斯分布的均值, μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)是 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)高斯分布的均值。
p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)是模型的预测分布,也可以写成 p θ ( x t − 1 ∣ x t , t ) p_{\theta}(x_{t-1}|x_t, t) pθ(xt−1∣xt,t)。
对上式展开,其中 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t, x_0) q(xt−1∣xt,x0)的均值 μ ~ ( x t , x 0 ) \tilde\mu(x_t, x_0) μ~(xt,x0)已经在前面计算出来了,直接代入:

上式中 ϵ \epsilon ϵ与上文的 z z z一样,都是加的噪声。下面的问题是,我们要最小化 L t − 1 − C L_{t-1}-C Lt−1−C,网络在模型中扮演什么角色?可选择的是:
- 预测 μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t),使其逼近 μ ~ ( x t , x 0 ) \tilde\mu(x_t, x_0) μ~(xt,x0),即损失是他俩的差;
- 预测 x 0 ′ x_0' x0′,使其直接逼近 x 0 x_0 x0,损失是他俩的差;
- 预测 ϵ \epsilon ϵ,这样对应的 x 0 ′ x_0' x0′就可以一步步地推出来(只是可以这么干,但是这样的话就与上个选择一样了,直接一步到位其实效果不好),这样 p θ ( x t − 1 ∣ x t , t ) p_{\theta}(x_{t-1}|x_t,t) pθ(xt−1∣xt,t)分布的均值 μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)就与 q ( x t − 1 ∣ x t , x 0 ′ ) q(x_{t-1}|x_t,x_0') q(xt−1∣xt,x0′)的均值公式一样,即下式。这样就可以逼近 μ ~ ( x t , x 0 ) \tilde\mu(x_t, x_0) μ~(xt,x0),即损失是他俩的差(可以简化计算);

扩散模型的作者选择用网络来预测 ϵ \epsilon ϵ,这样, μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)的计算公式如下:

再简化 L t − 1 − C L_{t-1}-C Lt−1−C,如下:

到这里,网络的损失就确定了,即最小化预测的噪声与实际添加的噪声的差,网络输入是时刻t和时刻t对应的xt。
有了网络输出的噪声后,就可以通过 p θ ( x t − 1 ∣ x t , t ) p_{\theta}(x_{t-1}|x_t,t) pθ(xt−1∣xt,t)分布的均值 μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)和方差(方差是预定义的 β \beta β)来采样出 x t − 1 x_{t-1} xt−1,训练过程和反扩散过程的伪代码如下:

反扩散过程用到了重参数化采样,上图中的 σ t \sigma_t σt就是标准差 β t \sqrt{\beta_t} βt。
相关文章:

扩散模型原理记录
1 扩散模型原理记录 参考资料: [1]【54、Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读】 https://www.bilibili.com/video/BV1b541197HX/?share_sourcecopy_web&vd_source7771b17ae75bc5131361e81a50a0c871 [2] https://t.bili…...

Metasploit高级技术【第九章】
预计更新第一章 Metasploit的使用和配置 1.1 安装和配置Metasploit 1.2 Metasploit的基础命令和选项 1.3 高级选项和配置 第二章 渗透测试的漏洞利用和攻击方法 1.1 渗透测试中常见的漏洞类型和利用方法 1.2 Metasploit的漏洞利用模块和选项 1.3 模块编写和自定义 第三章 Met…...

RK3568平台开发系列讲解(调试篇)IS_ERR函数的使用
🚀返回专栏总目录 文章目录 一、IS_ERR函数用法二、IS_ERR函数三、内核错误码沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将介绍 IS_ERR 函数的使用。 一、IS_ERR函数用法 先看下用法: 二、IS_ERR函数 对于任何一个指针来说,必然存在三种情况: 一种是合…...
TouchGFX界面开发 | TouchGFX软件安装
TouchGFX软件安装 TouchGFX和STemWin类似,都是一个GUI框架,可以方便的在STM32 Cortex-M4 以及更高级别的STM32芯片上创建GUI应用程序。 本文中的TouchGFX软件安装,是基于已经安装有STM32CubeMX Keil MDK-ARM开发环境的情况下进行的&#x…...
使用 IDEA 远程 Debug 调试
背景 有时候我们需要进行远程的debug,本文研究如何进行远程debug,以及使用 IDEA 远程debug的过程中的细节。看完可以解决你的一些疑惑。 配置 远程debug的服务,以springboot微服务为例。首先,启动springboot需要加上特定的参数。…...

红黑树和平衡二叉树的优缺点及应用场景
红黑树和平衡二叉树都是为了解决二叉搜索树的缺陷而提出的自平衡二叉树结构。它们的优缺点和应用场景如下: 红黑树: 优点: 时间复杂度为O(logN),可以快速查找、插入和删除。 红黑树具有良好的平衡性,树的高度保持较小,因此查找效率较高。 缺点: 实现比较复杂,需要遵守红黑树的…...

软文推广:真实有效提升软文排名与收录的三大方法!
软文是一种具有良好传播效果的文体,可以通过在搜索引擎中排名靠前的方式,为品牌或企业带来更多曝光。但是,如何让软文在搜索引擎中得到更好的收录和排名呢?在本文中,我们将讨论如何提升软文的收录和排名,以…...

SElinux的介绍及配置
SELinux(Security-Enhanced Linux) 是美国国家安全局(NSA)对于强制访问控制的实现,是 Linux历史上最杰出的新安全子系统 SELinux安全增强型Linux系统,是Linux内核子系统,旨在最大限度的减少服务进程对文件、端口等资源…...

vscode-python环境配置
vscode-python环境配置 1、环境基础 下载vscode找到python插件并安装安装python环境并配置环境变量 2、选择python解释器 尝试执行了一下,直接运行py文件,会使用c的调试工具,需要告诉vscode哪些是python Ctrl Shift P打开命令面板 执行…...
问卷调查样本量的确定方法
我们在进行问卷调查的时候,问卷的收集数量是重要的流程之一。问卷数量取决于几个因素,包括研究的目的和研究的类型。接下来,我们就聊一聊怎么确定所需的调查问卷数量。 1、确定研究目标。 确定所需问卷数量的第一步是明确研究目标。这一步是…...
:学习Swift的设计模式)
ios客户端学习笔记(三):学习Swift的设计模式
设计模式是指在软件开发中常用的一些解决问题的方法和思想,它可以帮助你更好地组织代码和提高代码的可维护性。你需要学习常见的设计模式,如MVC、MVVM、单例模式、工厂模式等,在开发应用程序时应用它们。 当你学习常见的设计模式时ÿ…...
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。 请你重新构造并返回输入数组 peopl…...

ESP32使用ESP-NOW协议实现一对多通信和MAC地址存储
目录 介绍ESP-NOW 协议概述在 ESP32 上配置 ESP-NOW使用 ESP-NOW 进行一对多通信在 ESP32 上存储发件人的 MAC 地址代码结论 介绍 ESP32 是一款功能强大的 Wi-Fi 和蓝牙双模模块,可用于使用 ESP-NOW 协议实现低功耗、高效率的一对多通信。本文将介绍如何使用ESP-NO…...
Qt 学生信息数据库管理
1 添加样式表 我们采用了样式表 通过添加Qt resources文件 添加前缀 添加文件,将我们的图标进行添加 2 拖动部件 用到的部件 Label 标签Pushbutton 按钮table view 视图LineEdit 输入框 3 程序编写 1 配置sql环境 在 pro文件中 添加 连接数据库跟访问数据…...
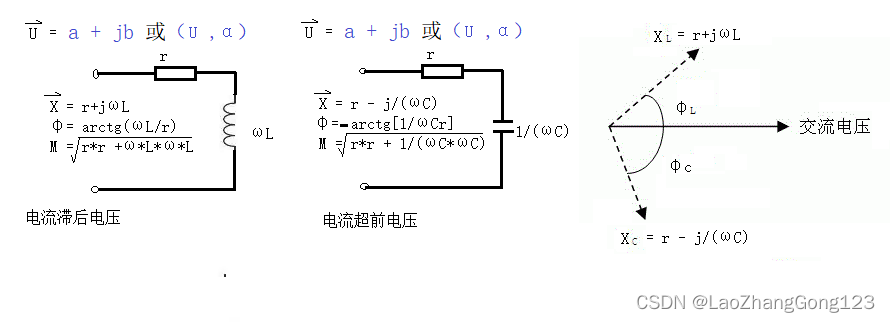
相量的加减乘除计算
相量的加减乘除计算 矢量是物理学中的术语,是指具有大小(magnitude)和方向的量。如速度、加速度、力等等就是这样的量。向量是数学中的术语,也称为欧几里得向量、几何向量、矢量。与向量对应的量叫做数量,在物理学中称…...

JavaScript 代码整洁之道
文章目录 概述篇变量篇函数篇注释篇异常处理篇复杂判断函数篇重构篇代码风格常量大写先声明后调用注释 参考资料 概述篇 书写能让人读懂的代码使用英语编写代码团队协作 制定通用的规则,依靠工具让团队的代码风格保持统一,要让代码看起来是由一个人编写…...
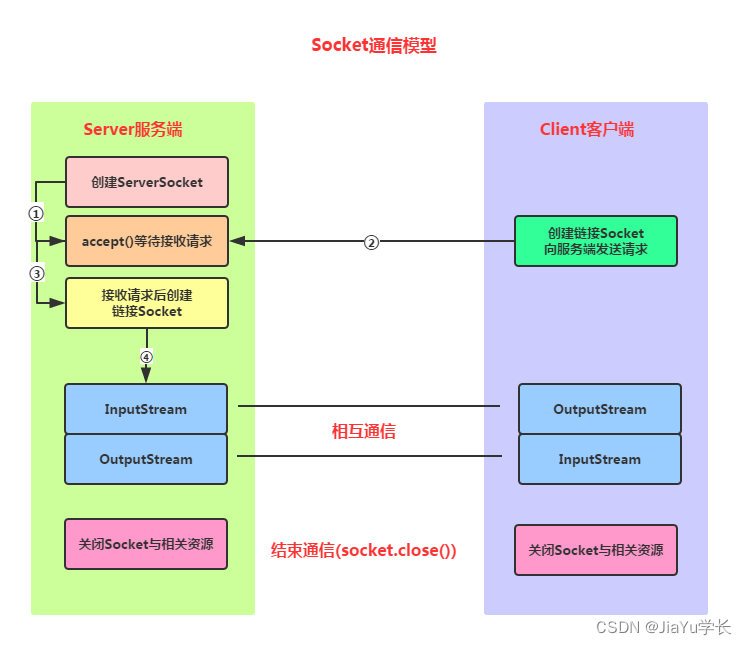
socket 及 字节序转换(嵌入式学习)
socket 及 字节序转换 socket简介Socket为什么需要Socket?socket类型Socket通信模型 字节序主机字节序到网络字节序网络字节序到主机字节序IP地址转换 socket简介 1、1982 - Berkeley Software Distributions 操作系统引入了socket作为本地进程之间通信的接口 2、1…...
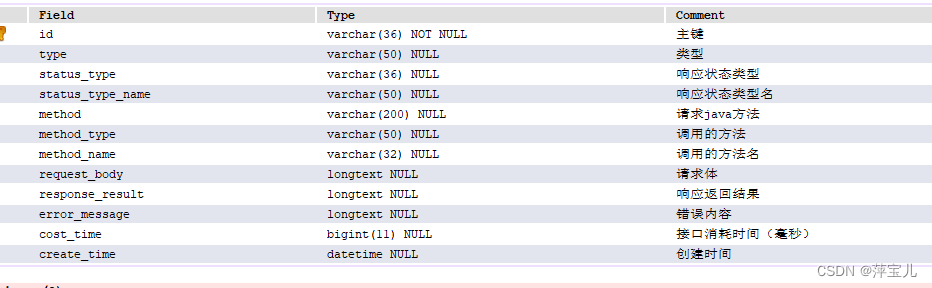
Java之~ Aop自定义注解日志
大纲步骤: 一,创建需要记录的日志表,创建基础方法。(省略) 二,在需要加记录日志的方法上加Aop注解1,创建一个注解类,Aop中定义一个注解import java.lang.annotation.*; /*** http 请…...

编译原理个人作业--第四章
构造FIRST和FOLLOW的大白话网站 第四章 1 考虑文法 G 1 G_1 G1: S → a ∣ ∧ ∣ ( T ) T → T , S ∣ S S \rightarrow a|\land|(T) \\ T\rightarrow T,S|S S→a∣∧∣(T)T→T,S∣S 先复习左递归如何消除 原书p69页 类似于 P → P a ∣ b P\rightarrow Pa|b P→Pa∣b的…...

学习笔记:数据库简介
数据库是一系列可以方便的访问和修改的数据的集合。 所有数据库管理系统的主要工作都是可靠的存储数据并使其对用户可用。 目前最常见的数据库模型主要是两种,即关系型数据库和非关系型数据库。 一、按数据的组织方式 数据从组织的角度上,主要分为结…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
