第一次参加CSDN周赛,这体验很难说···

👨💻个人主页:@花无缺
欢迎 点赞👍 收藏⭐ 留言📝 加关注✅!
本文由 花无缺 原创本文章收录于专栏 【CSDN周赛】
本篇文章目录
- 🌏前言
- 🌏一、勾股数
- 🌸题目描述
- 🌸题解
- 🌏二、最近的回文数
- 🌸题目描述
- 🌸题解
🌏前言
最近参加了 CSDN 官方举办的算法竞赛,恰好最近在学数据结构和算法,于是就顺带参加了第 45 期竞赛,比赛时间是两个小时,这次只有两个算法题,然后几个选择题,一个判断题。
算法题的难度我觉得一般吧,我都做出来了,但是第二个题目有 bug,一直不能通过,应该是测试用例的数据范围有问题。比赛过程中就只能通过 10% 的测试用例,但是后面自己在本地 IDE 里是可以通过题目要求的,希望以后官方大大审题能够更加仔细吧。
下面给大家讲讲这两个题。
🌏一、勾股数
🌸题目描述
勾股数是一组三个正整数,它们可以作为直角三角形的三条边。 比如3 4 5就是一组勾股数。 如果给出一组勾股数其中的两个,你能找出余下的一个吗?
输入输出:输入两个正整数,输出一个正整数表示满足勾股数的另一个数字,如果没有满足条件的第三个数,则输出 -1。
🌸题解
解题思路:这个题要求我们判断是否有对应的第三个数与已知的两个数构成勾股数,而勾股数必须要满足条件式:a*a + b*b = c*c;即两个较小的数的平方之和等于最大数的平方和,在三角形中,也即两直角边的平方之和等于斜边的平方。但是这里我们并不确定输入的两个数是直角边还是斜边,那么我们可以进行枚举,将这两个已知的数字分别作为斜边和两个直角边,这样就可以得出是否有第三个数与之构成勾股数了。
题解如下:
// CSDN周赛 45期 NO.1
// 花无缺题解
#include <iostream>
#include <math.h>
using namespace std;
int main() {long a,b;cin >> a >> b;long n = 0;long c; // c 为第三个数 // a 和 b 作为两个直角边, c 为斜边 // 开平方根函数返回的是一个浮点数, 向下取整c = sqrt(a*a + b*b);if (c*c==a*a+b*b) {cout << c;n++;}// a 为 斜边, b 和 c 为直角边 c = sqrt(a*a - b*b);if (a*a-b*b==c*c) {cout << c;n++;}// b 为斜边, a 和 c 为直角边 c = sqrt(b*b - a*a);if (b*b-a*a==c*c) {cout << c;n++;}// 如果 n 为 0, 那么说明没有满足成为勾股数的第 3 个数, 输出 -1 if (n==0)cout << -1;return 0;
}
🌏二、最近的回文数
🌸题目描述
回文数是一个非负整数,它的各位数字从高位到低位和从低位到高位的排列是相同的。 以下是一些回文数的例子: 0 133 525 7997 37273 现在给到一个数,求离它最近的一个回文数(离与它的差的绝对值最小)。如果这个数本身就是回文数,那么就输出它本身。
输入输出:输入一个正整数,输出与它最近的回文数。
🌸题解
解题思路:这个题顾名思义就是求回文数,使用一个 for 循环就可以求出最接近的回文数了,但是这里就出现 bug 了,比如数字 176,它的前面有一个回文数 171,后面有一个回文数 181,它们和176的差值的绝对值都是 5,那么我们应该输出 171 还是 181 呢,题目也没有给出说明,所以这个题问题有点大啊。
以下代码给大家参考下:
欢迎大家提出自己的想法
// CSDN周赛 45期 NO.2
// 花无缺题解
#include <iostream>
using namespace std;// 判断是否为回文数
bool palindrome(int n) {long x=0;long a=n;while (n) {x = n%10 + x*10;n /= 10;}if (x == a)return true;return false;
}int main() {long n;cin >> n;for (long i=n;; i++) {if (palindrome(i)) {cout << i;return 0;}}return 0;
}🌸欢迎
关注我的博客:@花无缺
持续为你输出有价值的内容~
🥇往期精彩好文:
📢【蓝桥杯省赛感想】
📢【CSS列表详解】
你们的点赞👍 收藏⭐ 留言📝 关注✅
是我持续创作,输出优质内容的最大动力!
谢谢!
相关文章:

第一次参加CSDN周赛,这体验很难说···
👨💻个人主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 本文章收录于专栏 【CSDN周赛】 本篇文章目录 🌏前言🌏一、勾股数🌸题目描述🌸题解 &a…...

8.DRF组件之认证、权限
DRF(Django Rest Framework)提供了一套权限和身份认证系统,可以在视图中进行配置。权限系统用于控制用户对资源的访问权限,身份认证系统用于验证用户的身份信息。 DRF支持以下几种权限控制方式: AllowAny:不做任何验证,允许所有用户访问。 IsAuthenticated:只允许已经…...

初识Tkinter弹窗
Tkinter弹窗 Tkinter是什么 Tkinter 是使用 python 进行窗口视窗设计的模块。Tkinter模块(“Tk 接口”)是Python的标准Tk GUI工具包的接口。作为 python 特定的GUI界面,是一个图像的窗口,tkinter是python 自带的,可以编辑的GUI界面ÿ…...

设计模式之责任链模式(C++)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 一、责任链模式是什么? 责任链模式是一种行为型的软件设计模式,对象内存在对下家的引用,层层连…...

音游判定原理详解——从触摸屏幕到判定音符【Project SEKAI攻略】
“音乐游戏”一般简称为“音游”,玩家需要配合音乐的节奏来进行一定的动作。 《Project SEKAI》作为一个“移动端音游”,绝大多数玩家会使用手机、平板电脑等移动设备的触摸屏进行游玩,也有极少数的玩家不按常理出牌,使用手台、键…...

【论文阅读】Self-Paced Boost Learning for Classification
论文下载 bib: INPROCEEDINGS{PiLi2016SPBL,title {Self-Paced Boost Learning for Classification},author {Te Pi and Xi Li and Zhongfei Zhang and Deyu Meng and Fei Wu and Jun Xiao and Yueting Zhuang},booktitle {IJCAI},year {2016},pages {1932--1938} …...

通过CSIG—走进合合信息探讨生成式AI及文档图像处理的前景和价值
一、前言 最近有幸参加了由中国图象图形学学会(CSIG)主办,合合信息、CSIG文档图像分析与识别专业委员会联合承办的“CSIG企业行——走进合合信息”的分享会,这次活动以“图文智能处理与多场景应用技术展望”为主题,聚…...
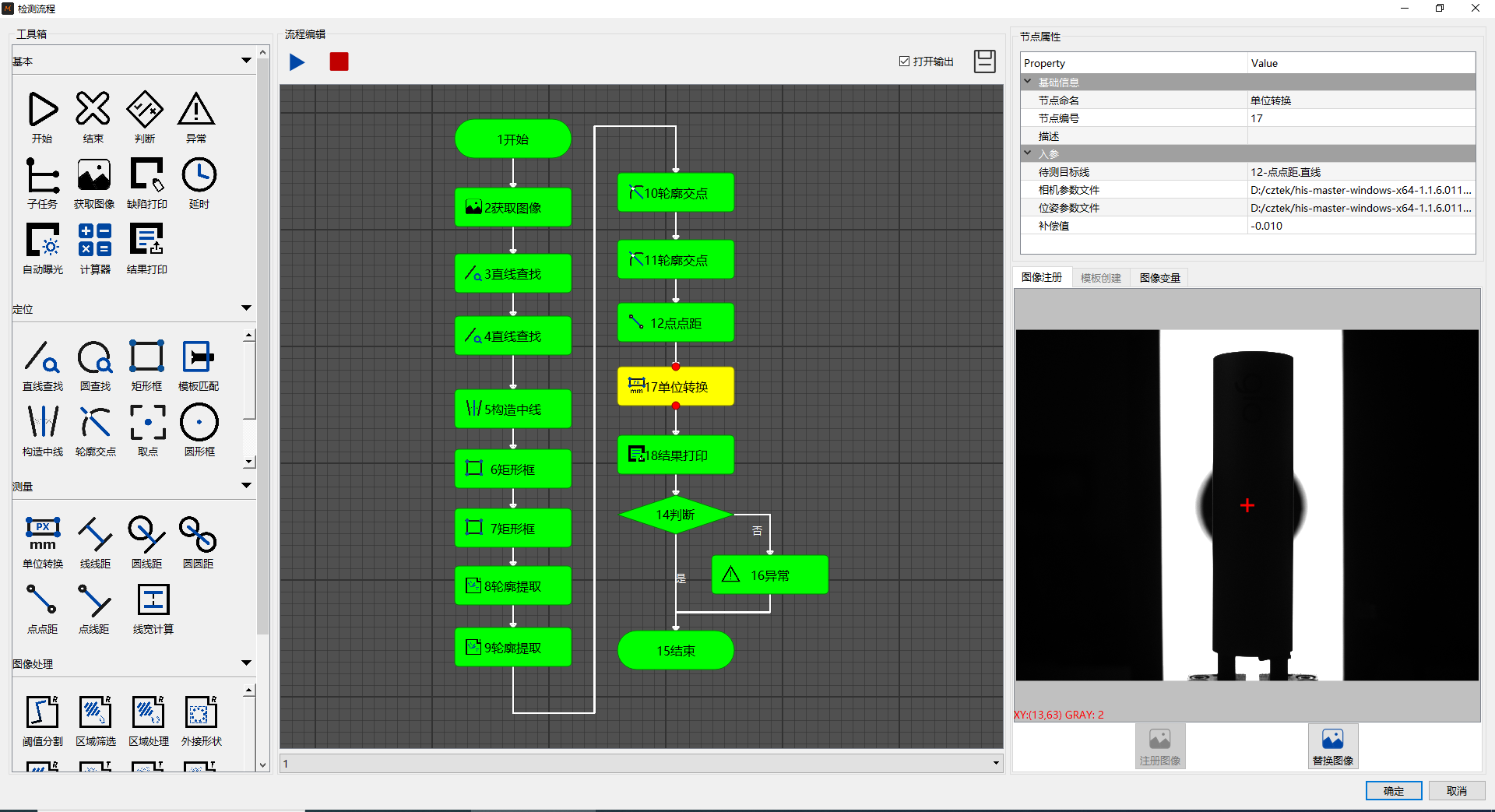
流程图拖拽视觉编程--概述
一般的机器视觉平台采用纯代码的编程方式,如opencv、halcon,使用门槛高、难度大、定制性强、开发周期长,因此迫切需要一个低代码开发的视觉应用平台。AOI缺陷检测的对象往往缺陷种类多,将常用的图像处理算子封装成图形节点,如抓直…...

深度学习中的卷积神经网络
博主简介 博主是一名大二学生,主攻人工智能研究。感谢让我们在CSDN相遇,博主致力于在这里分享关于人工智能,c,Python,爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主,博主会继续更新的,…...
vue3的介绍和两种创建方式(cli和vite)
目录 一、vue3的介绍 (一)vue3的简介 (二)vue3对比vue2带来的性能提升 二、vue3的两种创建方式 方式一:使用vue-cli创建(推荐--全面) 操作步骤 方式二:使用vite创建 操作步…...

camunda工作流user task如何使用
在Camunda中使用User Task通常需要以下步骤: 1、创建User Task:使用BPMN 2.0图形化设计器(如Camunda Modeler),将User Task元素拖到流程图中,并为任务命名,指定参与者(用户或用户组…...

三元运算符
三元运算符 三元运算符通常在Python⾥被称为条件表达式 这些表达式基于真(true)/假(not)的条件判 断 在Python 2.4以上才有了三元操作。 下⾯是⼀个伪代码和例⼦: 伪代码: 如果条件为真,返回真 否则返回假 condition_is_true if condition else c…...
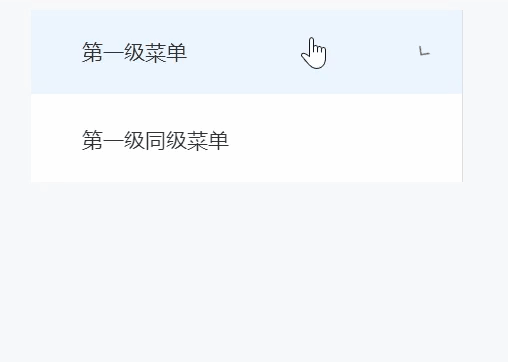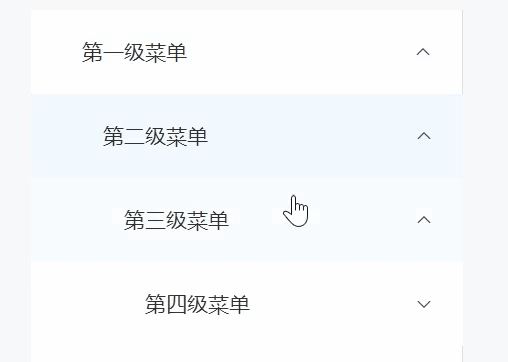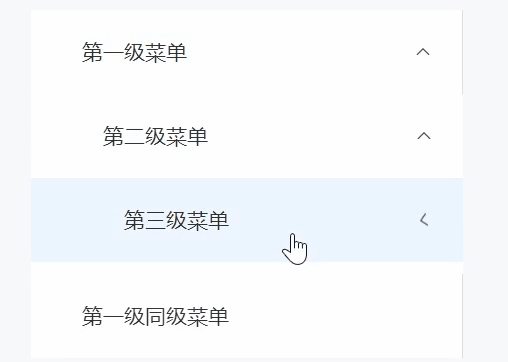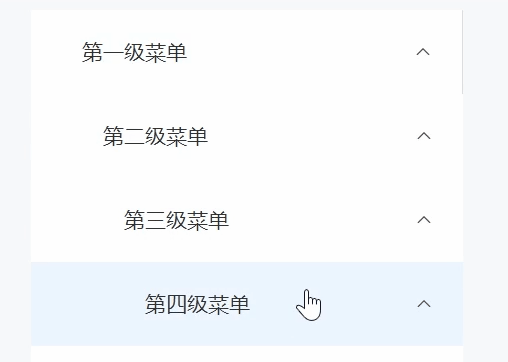
Vue3 Element-plus el-menu无限级菜单组件封装
对于element中提供给我们的el-menu组件最多可以实现三层嵌套,如果多一层数据只能自己通过变量去加一层,如果加了两层、三层这种往往是行不通的,所以只能进行封装 效果图 一、定义数据 MenuData.ts export default [{id: "1",name…...
( “树” 之 BST) 669. 修剪二叉搜索树 ——【Leetcode每日一题】
二叉查找树(BST):根节点大于等于左子树所有节点,小于等于右子树所有节点。 二叉查找树中序遍历有序。 669. 修剪二叉搜索树 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树&…...

【C语言】浅涉结构体(声明、定义、类型、定义及初始化、成员访问及传参)
简单不先于复杂,而是在复杂之后。 目录 1. 结构体的声明 1.1 结构体的基础知识 1.2 结构的声明 1.3 结构成员的类型 1.4 结构体变量的定义和初始化 2. 结构体成员的访问 3. 结构体传参 1. 结构体的声明 1.1 结构体的基础知识 结构是一些值的集合&…...
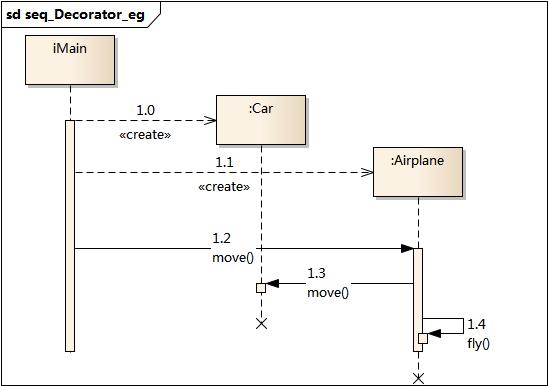
设计模式-结构型模式之装饰模式
3. 装饰模式 3.1. 模式动机 一般有两种方式可以实现给一个类或对象增加行为: 继承机制 使用继承机制是给现有类添加功能的一种有效途径,通过继承一个现有类可以使得子类在拥有自身方法的同时还拥有父类的方法。但是这种方法是静态的,用户不能…...
第九课 朴素贝叶斯分类器的工作原理 机器学习算法)
【Chatgpt4 教学】 NLP(自然语言处理)第九课 朴素贝叶斯分类器的工作原理 机器学习算法
我在起,点更新NLP自然语言处理》《王老师带我成为救世主》 为啥为它单独开章,因为它值得,它成功的让我断了一更,让我实践了自上而下找能够理解的知识点,然后自下而上的学习给自己的知识升级,将自己提升到能…...

基于html+css的图片展示17
准备项目 项目开发工具 Visual Studio Code 1.44.2 版本: 1.44.2 提交: ff915844119ce9485abfe8aa9076ec76b5300ddd 日期: 2020-04-16T16:36:23.138Z Electron: 7.1.11 Chrome: 78.0.3904.130 Node.js: 12.8.1 V8: 7.8.279.23-electron.0 OS: Windows_NT x64 10.0.19044 项目…...
Jupyter Notebook小知识
目录 1 快捷键1.1 常用快捷键1.2 魔法函数 2 常用快捷键2.1 模式切换2.2 命令模式快捷键2.3 编辑模式快捷键3 Matplotlib绘图 4 小技巧4.1 文件默认目录的查看以及更改4.2 更改主题颜色 5 其它5.1 python中 r, b, u, f 的含义5.2 f/format():格式化操作 6 常见问题6.1 查看模块…...
redis原理及进化之路
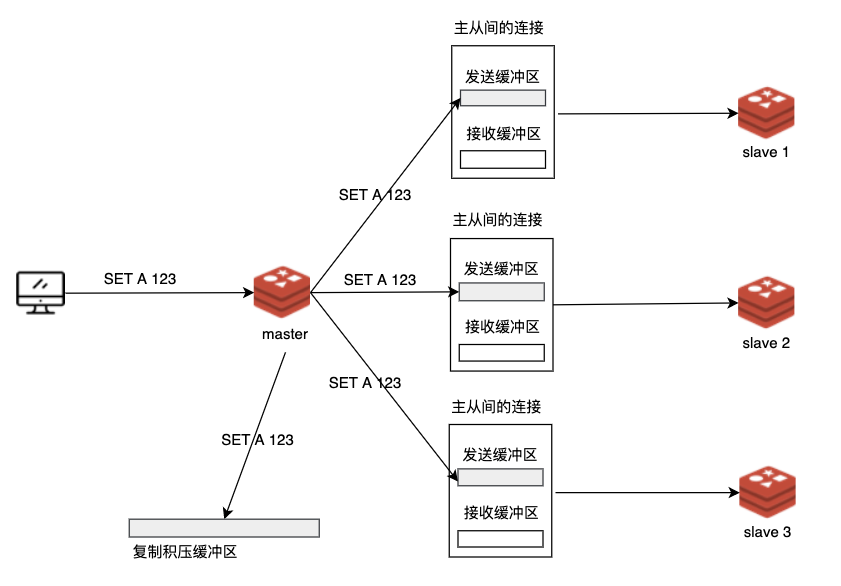
Redis 的主从复制经历了多次演进,本文将从最基本的原理和实现讲起,并层层递进,逐步呈现 Redis 主从复制的演进历史。大家将了解到 Redis 主从复制的原理,以及各个改进版本解决了什么问题,并最终看清 Redis 7.0 主从复制…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
