LeetCode:59. 螺旋矩阵 II
🌻算法,不如说它是一种思考方式🍀
算法专栏: 👉🏻123
一、🌱59. 螺旋矩阵 II
- 题目描述:给你一个正整数
n,生成一个包含 1 到n2 所有元素,且元素按顺时针顺序螺旋排列的nxn正方形矩阵matrix。 - 来源:力扣(LeetCode)
- 难度:中等
- 提示:
1 <= n <= 20 - 示例 1:
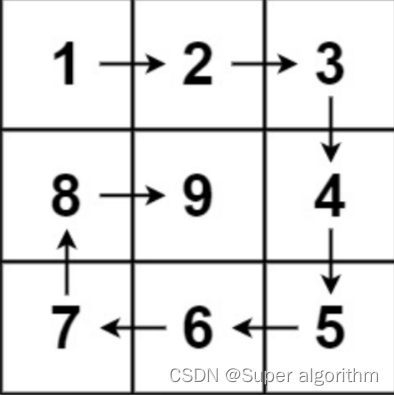
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
🌴解题
模拟方向
本题只需要考虑:右 下 左 上,四种走向是循环来的,因此定义一个变量 direction,分别赋值 0 右,1 下,2 左,3 上,每个走向结束就 +1 再对 4 取余。
右 下 左 上 四个走向其实只需要控制 x y 坐标的某一个进行加减,主要是判断何时到达边界:数组边界、数组有值。
code:
class Solution {public int[][] generateMatrix(int n) {int[][] ans=new int[n][n];if(n==1) {ans[0][0] = 1;return ans;}int direction=0;//0右 1下 2左 3上int i=0,j=-1;//坐标int k = 1;boolean tag=true;while(tag){switch (direction){case 0:j++;for (; j < n; j++) {if(ans[i][j]!=0)break;ans[i][j]=k;k++;}j--;direction=(direction + 1) % 4;if(ans[i+1][j]!=0)tag=false;break;case 1:i++;for (; i < n; i++) {if(ans[i][j]!=0)break;ans[i][j]=k;k++;}i--;direction=(direction + 1) % 4;if(ans[i][j-1]!=0)tag=false;break;case 2:j--;for (; j >=0 ; j--) {if(ans[i][j]!=0) {break;}ans[i][j]=k;k++;}j++;direction=(direction + 1) % 4;if(ans[i-1][j]!=0)tag=false;break;case 3:i--;for (; i >=0; i--) {if(ans[i][j]!=0)break;ans[i][j]=k;k++;}i++;direction=(direction + 1) % 4;if(ans[i][j+1]!=0)tag=false;break;}}return ans;}
}

返回第一页。☝
陶渊明(352 或 365 年 — 427 年),字元亮,又名潜,私谥“靖节”,世称靖节先生,浔阳柴桑(今江西省九江市)人。东晋末至南朝宋初期伟大的诗人、辞赋家。
☕物有本末,事有终始,知所先后。🍭
🍎☝☝☝☝☝我的CSDN☝☝☝☝☝☝🍓
相关文章:

LeetCode:59. 螺旋矩阵 II
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀 算法专栏: 👉🏻123 一、🌱59. 螺旋矩阵 II 题目描述:给你一个正整数 n ,…...

信息安全复习六:公开密钥密码学
一、章节梗概 1.公开密钥密码模型的基本原理 2.两个算法:RSA&D-H算法 主要内容 1.对称密钥密码的密钥交换问题 2.公钥密码模型的提出 3.设计公钥密码的基本要求 4.数字签名 5.RSA算法 6.公钥密码的特征总结 二、对称密钥密码 对称加密算法中,数据…...

YOLOv8 更换主干网络之 ShuffleNetv2
《ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design》 目前,神经网络架构设计多以计算复杂度的间接度量——FLOPs为指导。然而,直接的度量,如速度,也取决于其他因素,如内存访问成本和平台特性。因此,这项工作建议评估目标平台上的直接度量,而…...

async/await最详细的讲解
一、async 和 await 在干什么 async 是“异步”的简写,而 await 的意思是等待。async 用于申明一个 function 是异步的,而 await 等待某个操作完成。 async/await 是一种编写异步代码的新方法。之前异步代码的方案是回调和 promise。 async/await 像 p…...

学习数据结构第6天(栈的基本概念)
栈的基本概念 栈的定义栈的基本操作栈的存储结构 栈的定义 栈(Stack)是一种基于先进后出(FILO)或者后进先出(LIFO)的数据结构,是一种只允许在一端进行插入和删除操作的特殊线性表。 栈按照先进后出的原则存储数据,先进入的数据被压入栈底,最…...

自动化添加时间戳版本号
自动化添加时间戳版本号 前言一、静态资源二、版本号的来源三. 版本信息的位置四. 添加时间戳版本号1. 手动添加2. 自动化生成 前言 软件开发和发布过程中,版本是个极其重要的因素。大至操作系统,小到功能组件,都会涉及到版本相关的问题。 …...

【C语言】指针进阶[上] (字符、数组指针、指针数组、数组传参和指针传参)
简单不先于复杂,而是在复杂之后。 目录 1. 字符指针 面试题 2. 指针数组 3. 数组指针 3.1 数组指针的定义 3.2 &数组名 VS 数组名 3.3 数组指针的使用 4. 数组参数、指针参数 4.1 一维数组传参 4.2 二维数组传参 4.3 一级指针传参 4.4 二…...

软件测试外包干了4年,感觉废了..
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
ai改写句子软件-ai改写
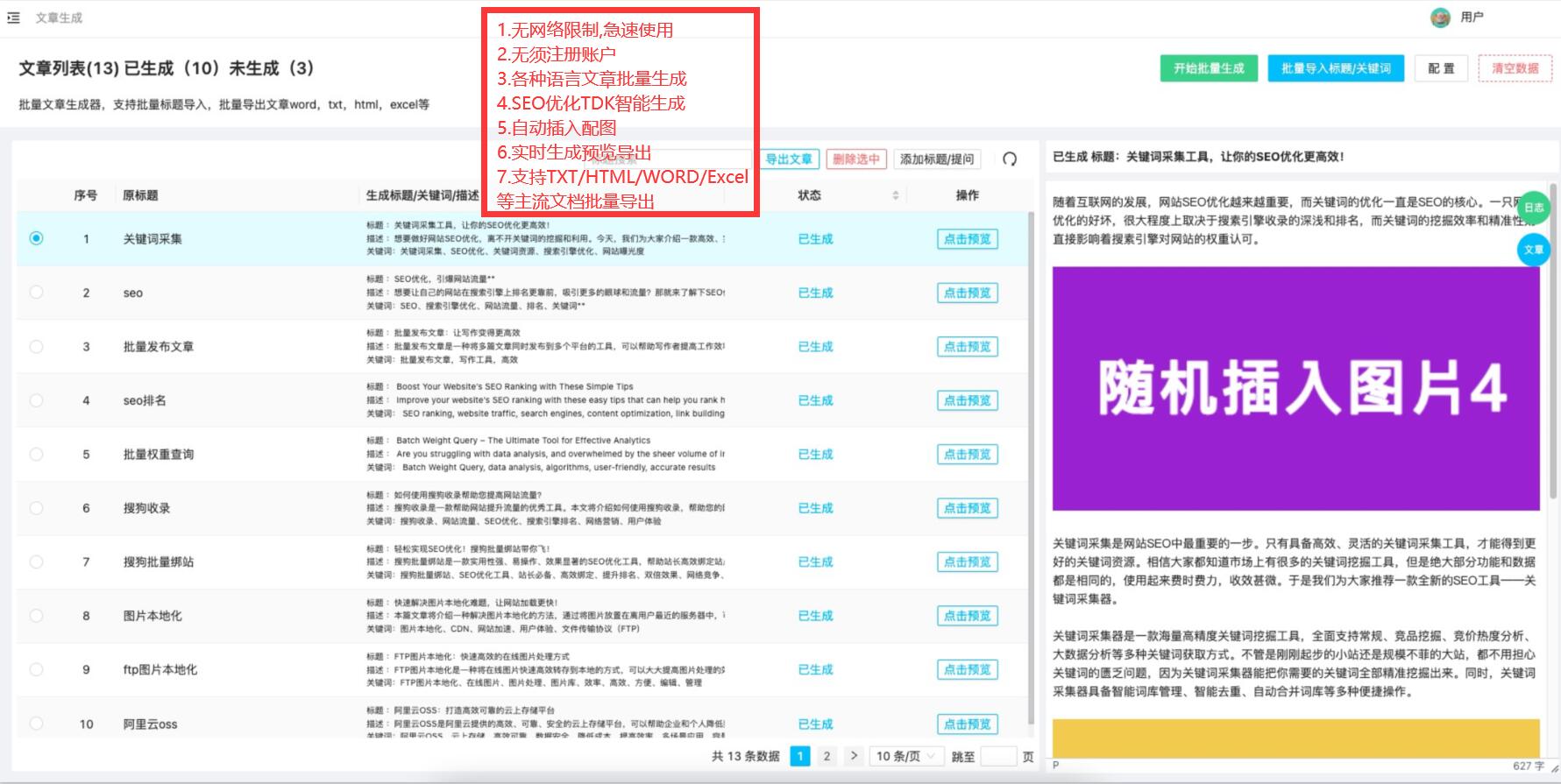
AI免费伪原创:助力网站内容升级 您是否曾经为网站优化而烦恼,无论是内容更新还是SEO优化,都需要大量的时间和精力。但是,您是否知道,现在有一款能够使用AI技术来帮助您完成这些任务,而且还是免费的呢&…...
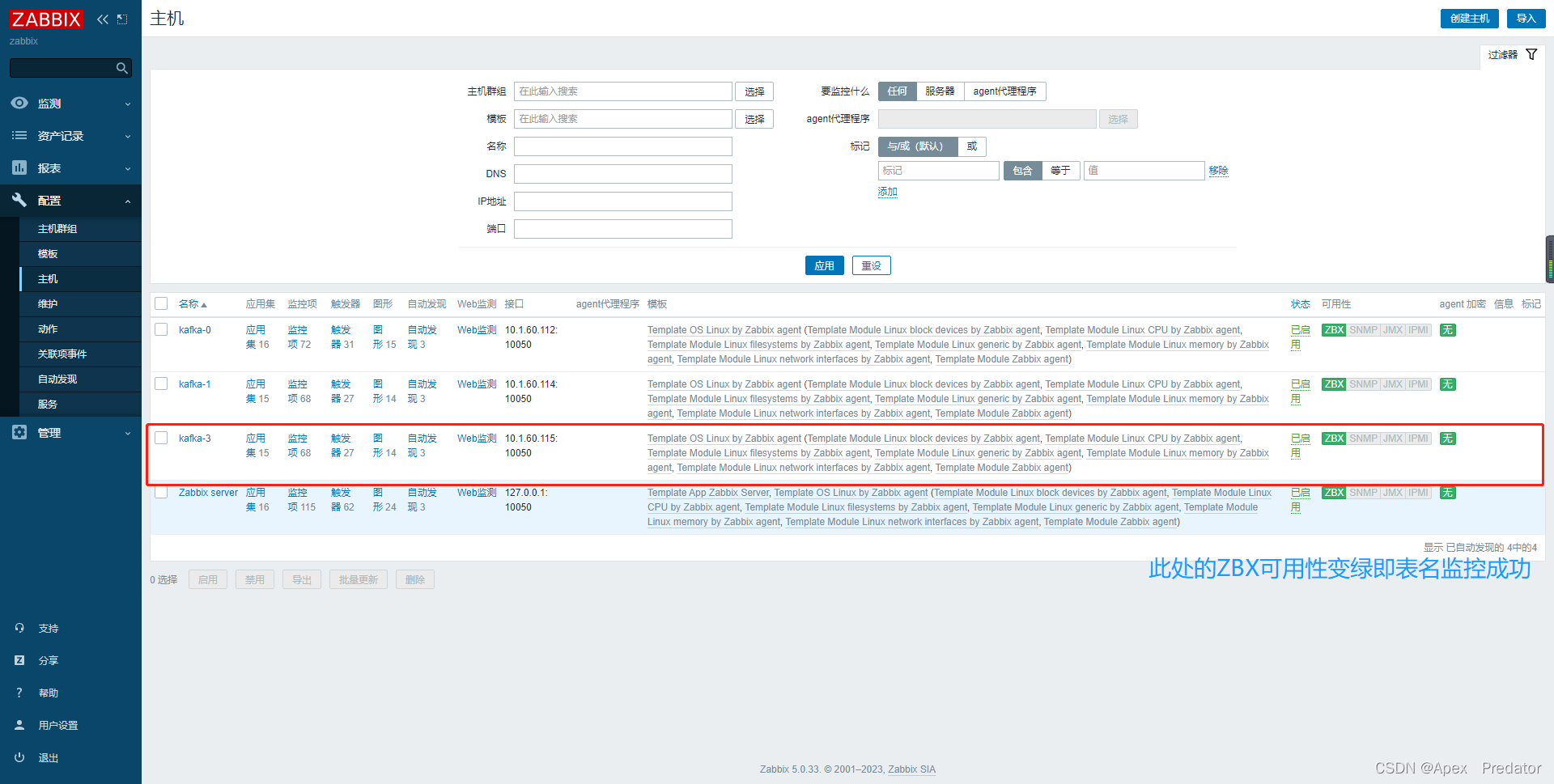
zabbix监控linux主机
1.本实验使用centos7主机,IP地址为10.1.60.115,firewalld和selinux服务已关闭 2.下载zabbix yum源(与zabbix server用一样的版本) rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm 3.安装zabbix客户…...

编程中泛型的使用规则和限制是什么?
泛型是一种程序设计风格,它允许程序员在编写代码时使用一些以后才指定的类型,在实例化时作为参数指明这些类型。泛型主要用于实现通用的数据结构,例如集合、映射、列表等,使得这些数据结构可以存储多种类型的元素。 在泛型使用之…...
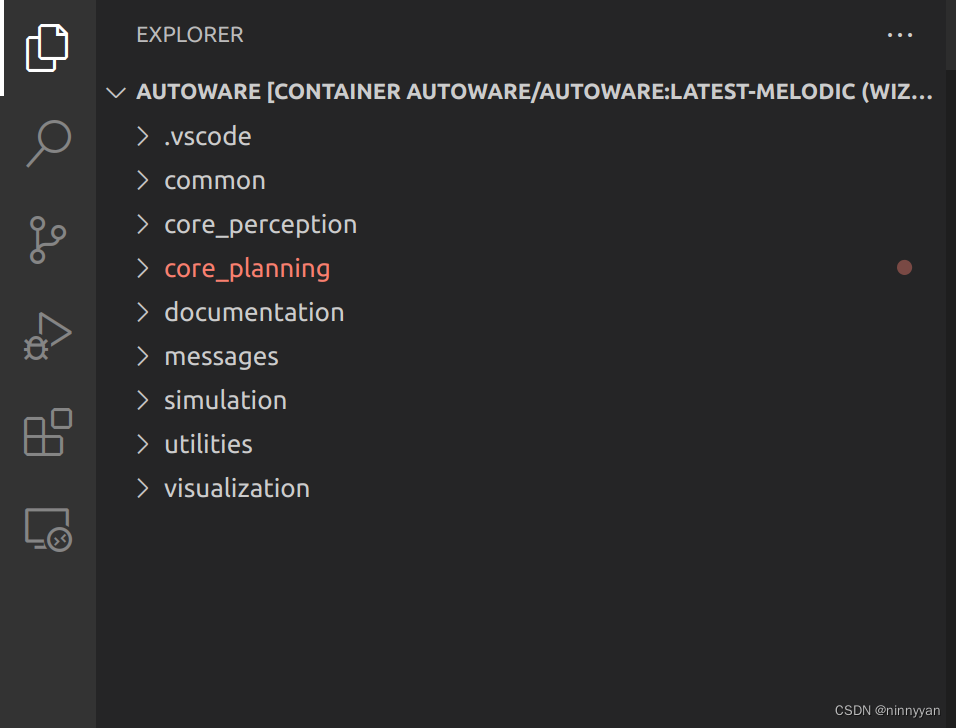
【工具】使用VS Code调试Docker Container中的代码
目录 使用VS Code调试Docker Container中的Autoware.ai代码第一种方法 -- 在VS Code中进行DebugStep1Step2Step3Step4c_cpp_properties.jsonlaunch.jsonsettings.jsontask.json Step5Step6Step7参考链接 第二种方法 -- cmake重新编译cmake使用方法(简介)…...

ZVL3网络分析仪
ZVL3 Rohde&Schwarz ZVL3 3G矢量网络分析仪|罗德与施瓦茨 9KHz至3GHz 罗德与施瓦茨Rohde&Schwarz 性能特点: 频率范围 9kHz至3GHz/6 GHz(典型值为5kHz) 测量时间(201个测量点,以校准的双端口) <75ms 数据传输(201个测量点) 在100Mbit/sLAN…...

TCP协议
传输层(协议) TCP协议 三次握手协议保证连接建立 四次挥手,利用这个协议断开连接,而且保证连接通道里面数据已经处理完毕 客户端(Socket): 1、创建客户端的Socket对象(Socket)与指…...

69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1࿱…...

Webshell应急响应指南
Webshell应急响应指南 1.Webshell 排查2.入侵时间确定3.Web日志分析4.漏洞分析5.漏洞复现6.清除Webshell并修复漏洞7.Webshell 防御方法1.Webshell 排查 可利用 Webshell 扫描工具(如 D 盾,河马)对应用部署目录进行扫描,如网站D:\WWW\目录 或者将当前网站目录文件与此前备…...
Linux如何定时执行任务
目录 crontab 介绍 安装crontab 服务操作说明 操作案例 crontab 介绍 Linux crontab是采用定期执行程序的命令,当安装完成操作 系统后,默认便会启动此任务调度命令,crond命令每分钟都会定期检查是否要执行任务的工作,如果要执…...

使用nvm替换nvmw作为nodejs的版本切换(亲测)
之前的文章:同时使用vue2.0和vue3.0版本的采坑记录 安装的nvmw,今天想要用nvmw切换时,居然给我报错了: 然后我就走上了使用nvm替换nvmw之路。。 1.安装 nvm-windows下载 下载release版 中Assets中的包,window10&…...
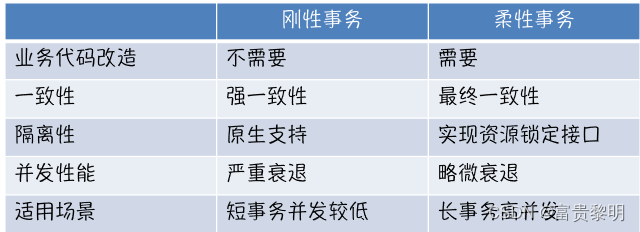
分布式事务
数据库事务 Atomicity 原子性 某个操作,要么全部执行完毕,要么全部回滚 Consistency 一致性 数据库中的数据全都符合现实世界的约束,则这些数据就符合一致性。 比如性别约束男or女,人名币面值不能为负数;出生地址不能…...

zk111111111111111111
Zookeeper 1 zookeeper(作为 dubbo 的注册中心): 概述: zookeper 是 一个分布式的、开源的分布式应用程序的协调服务,管理分布式应 用 作用: 配置管理,分布式锁,集群管理 2 zookeeper 的安装 (dubbo 的资料中已经整理) 3 zookeeper 的数据模型 zookeeper 是一个树形的服…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
