Codeforces Round 864 (Div. 2)(A~D)
A. Li Hua and Maze

给出两个不相邻的点,最少需要堵上几个方格,才能使得两个方格之间不能互相到达。
思路:显然,对于不邻任何边界的方格来说,最少需要的是4,即上下左右都堵上;邻一个边界就-1,两个方格取一下最小值即可。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 2e5 + 5;
int t, n, m, x1, y1, x2, y2;int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n >> m;std::cin >> x1 >> y1 >> x2 >> y2;int ans1 = 4, ans2 = 4;if(x1 == 1 || x1 == n) ans1 --;if(y1 == 1 || y1 == m) ans1 --;if(x2 == 1 || x2 == n) ans2 --;if(y2 == 1 || y2 == m) ans2 --;std::cout << std::min(ans1, ans2) << '\n';}return 0;
}B. Li Hua and Pattern

给出一个n*n的矩阵,操作k次,判断能否使得当前矩形和旋转180°后的图形完全相同。每次操作是将格子的颜色翻转。
思路:显然,将格子分为四部分,对角的两两都应该中心对称。对于两两方格的两个坐标有相加等于n+1的关系,判断一下即可。注意,对于奇数时的中心那一条,应该等于同一条线上的另一部分。对于操作次数k,如果小于不同的方格数,则一定不满足条件;若是大于k,n是偶数时,k-cnt必须是偶数。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 1e3 + 5;
int t, n, k;
int a[N][N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n >> k;for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {std::cin >> a[i][j];}}int m = (n + 1) / 2;int cnt = 0;for(int i = 1; i <= m; i ++) {for(int j = 1; j <= m; j ++) {if(a[i][j] != a[1 + n - i][1 + n - j])cnt ++;}}for(int i = m + 1; i <= n; i ++) {for(int j = 1; j <= n / 2; j ++) {if(a[i][j] != a[1 + n - i][1 + n - j])cnt ++;}}if(k < cnt || (k - cnt) % 2 && n % 2 == 0)std::cout << "NO" << '\n';elsestd::cout << "YES" << '\n';}return 0;
}C. Li Hua and Chess

 在n*m的方格中猜一个确定位置。每次可以询问目标位置和询问位置的距离,注意,距离是指经过八个方向移动的最小距离,在三次询问之内找到答案。
在n*m的方格中猜一个确定位置。每次可以询问目标位置和询问位置的距离,注意,距离是指经过八个方向移动的最小距离,在三次询问之内找到答案。
思路:观察移动方式,我们可以发现对于一个位置来说,向外扩展x圈上的点到中心点的距离都是x。那么我们可以先询问(1, 1)点,然后再问(1 + len, 1 + len)点,当然,注意和边界的判断。那么答案位置必然在第二次询问的点的正上方或者正左方。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 1e3 + 5;
int t, n, m;int ask(int x, int y) {std::cout << "? " << x << ' ' << y << '\n';std::cout.flush();int dis;std::cin >> dis;return dis;
}void work() {int a = 1, b = 1;int len = ask(a, b);if(!len) {std::cout << "! " << a << ' ' << b << '\n';return;}a = std::min(a + len, n), b = std::min(b + len, m);len = ask(a, b);if(!len) {std::cout << "! " << a << ' ' << b << '\n';return;}if(len >= a && len < b) {std::cout << "! " << a << ' ' << b - len << '\n';return;}else if(len >= b && len < a) {std::cout << "! " << a - len << ' ' << b << '\n';return;}int aa = a, bb = b, ll = len;a -= len;len = ask(a, b);if(!len) {std::cout << "! " << a << ' ' << b << '\n';return;}std::cout << "! " << aa << ' ' << bb - ll << '\n';
}int main() {// std::ios::sync_with_stdio(false);// std::cin.tie(0);// std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n >> m;work();std::cout.flush();}return 0;
}D. Li Hua and Tree

给出一棵树,进行k次操作,操作1是计算x的子树权值的和,操作2是交换x和x的重子,即断开x和x的父节点之间的边,链接x的重子和x的父节点之间的边。定义重子是x中具有最大子树的子节点,若有多个点满足条件,则重子是索引最小的那个点。
思路:模拟整个过程即可,注意细节。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
#define int long long
const int N = 1e5 + 5;
int n, m;
std::vector<int> vec[N];
int a[N], w[N], fa[N], val[N];struct node{int w, id;bool operator<(const node &a) const{if (w != a.w) return w > a.w;return id < a.id;}
};
std::set<node> s[N];void DFS(int u, int f){val[u] = a[u];w[u] = 1;for(auto v : vec[u]){if (v == f) continue;fa[v] = u;DFS(v, u);val[u] += val[v];w[u] += w[v];s[u].insert({w[v], v});}
}signed main(){std::cin.tie(0);std::cout.tie(0);std::ios::sync_with_stdio(0);std::cin >> n >> m;for(int i = 1; i <= n; i ++) {std::cin >> a[i];}for(int i = 1; i < n; i ++) {int u, v;std::cin >> u >> v;vec[u].push_back(v);vec[v].push_back(u);}DFS(1, -1);while(m --){int op, x;std::cin >> op >> x;if(op == 1) std::cout << val[x] << '\n';else {if (s[x].empty()) continue;int son = s[x].begin() -> id;s[fa[x]].erase({w[x], x});s[x].erase(s[x].begin());int big = w[son];int value = val[son];w[son] = w[x];w[x] -= big;val[son] = val[x];val[x] -= value;s[fa[x]].insert({w[son], son});s[son].insert({w[x], x});fa[son] = fa[x];fa[x] = son;}}return 0;
}
相关文章:

Codeforces Round 864 (Div. 2)(A~D)
A. Li Hua and Maze 给出两个不相邻的点,最少需要堵上几个方格,才能使得两个方格之间不能互相到达。 思路:显然,对于不邻任何边界的方格来说,最少需要的是4,即上下左右都堵上;邻一个边界就-1&a…...
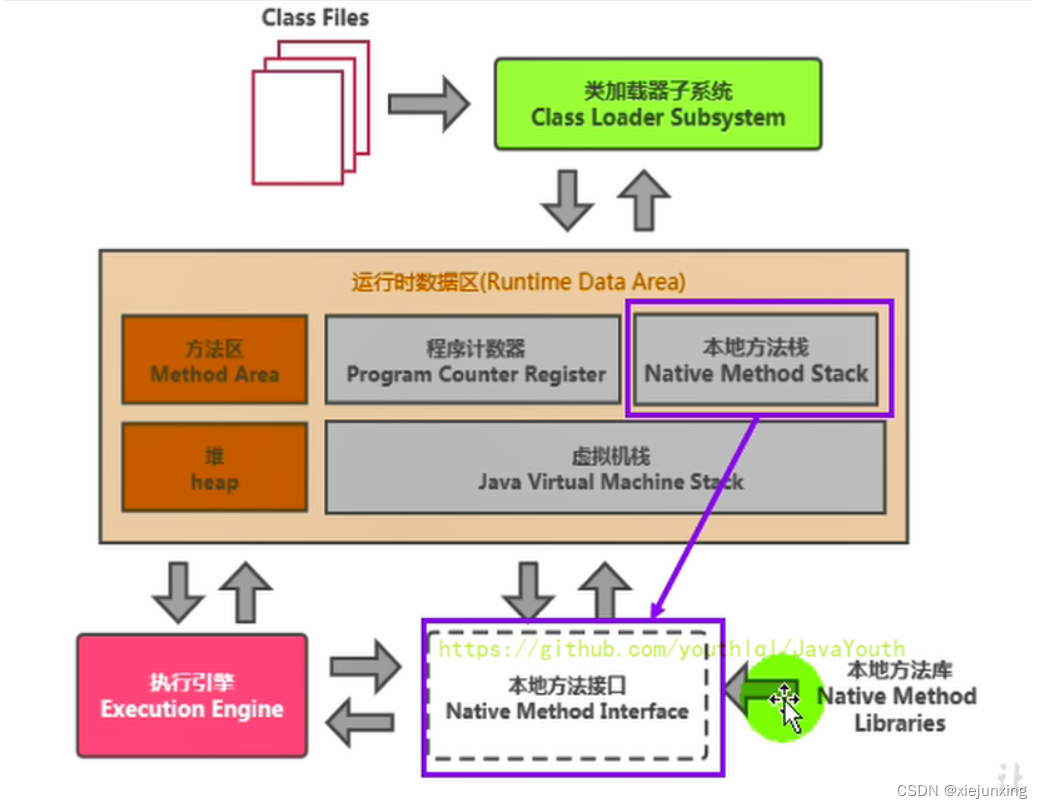
第3章-运行时数据区
此章把运行时数据区里比较少的地方讲一下。虚拟机栈,堆,方法区这些地方后续再讲。 转载https://gitee.com/youthlql/JavaYouth/tree/main/docs/JVM。 运行时数据区概述及线程 前言 本节主要讲的是运行时数据区,也就是下图这部分,…...
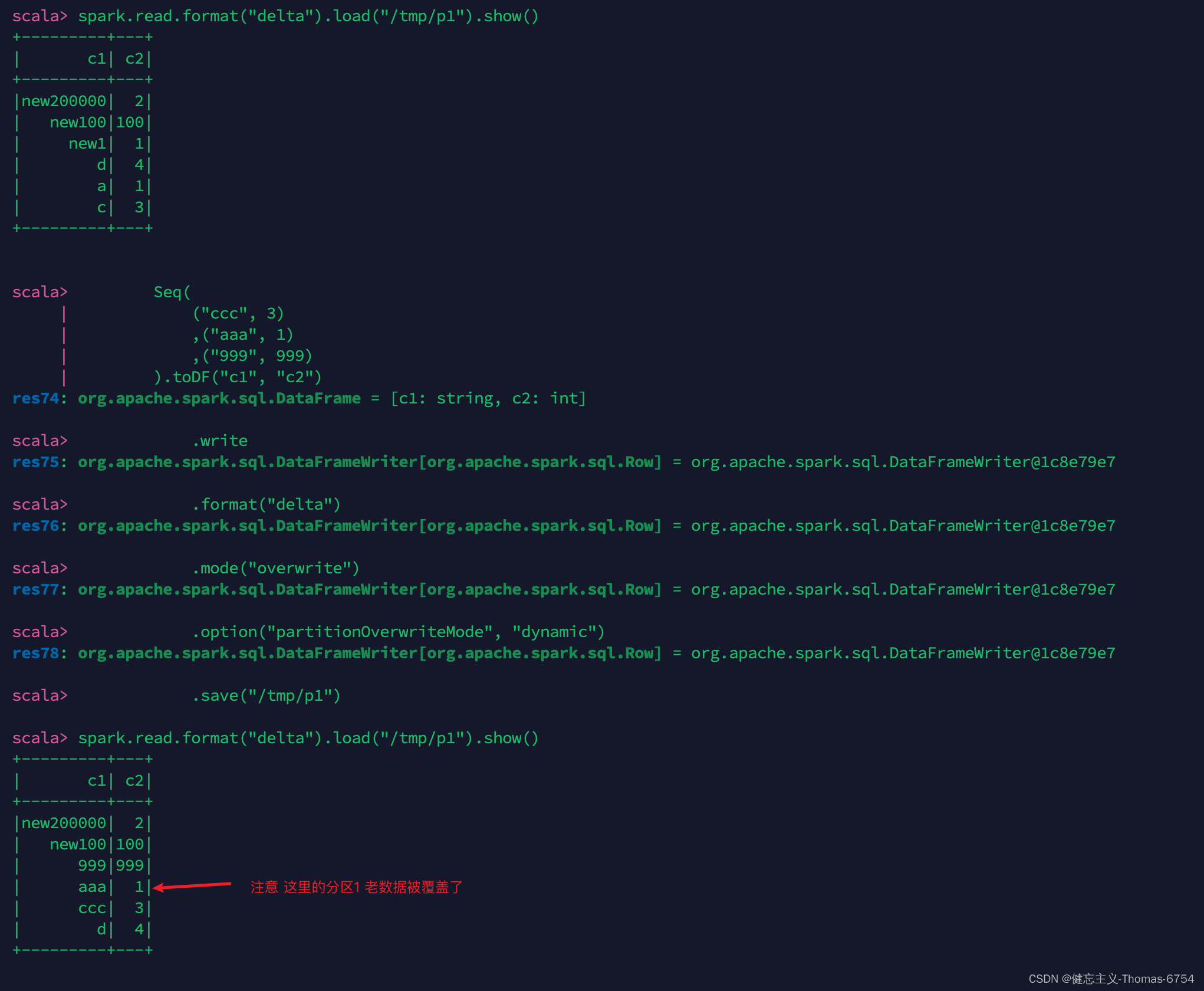
delta.io 参数 spark.databricks.delta.replaceWhere.constraintCheck.enabled
总结 默认值true 你写入的df分区字段必须全部符合覆盖条件 .option("replaceWhere", "c2 == 2") false: df1 overwrite tb1: df1中每个分区的处理逻辑: - tb1中存在(且谓词中匹配)的分区,则覆盖 - tb1中存在(谓词中不匹配)的分区,则append - tb1中不存…...

Redis知识点
1. Redis-常用数据结构 Redis提供了一些数据结构供我们往Redis中存取数据,最常用的的有5种,字符串(String)、哈希(Hash)、列表(list)、集合(set)、有序集合(zset…...
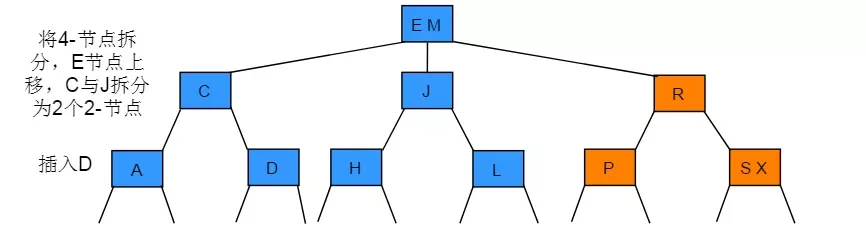
经典数据结构之2-3树
2-3树定义 2-3树,是最简单的B-树,其中2、3主要体现在每个非叶子节点都有2个或3个子节点,B-树即是平衡树,平衡树是为了解决不平衡树查询效率问题,常见的二叉平衡书有AVL树,它虽然提高了查询效率,…...

Numpy从入门到精通——节省内存|通用函数
这个专栏名为《Numpy从入门到精通》,顾名思义,是记录自己学习numpy的学习过程,也方便自己之后复盘!为深度学习的进一步学习奠定基础!希望能给大家带来帮助,爱睡觉的咋祝您生活愉快! 这一篇介绍《…...
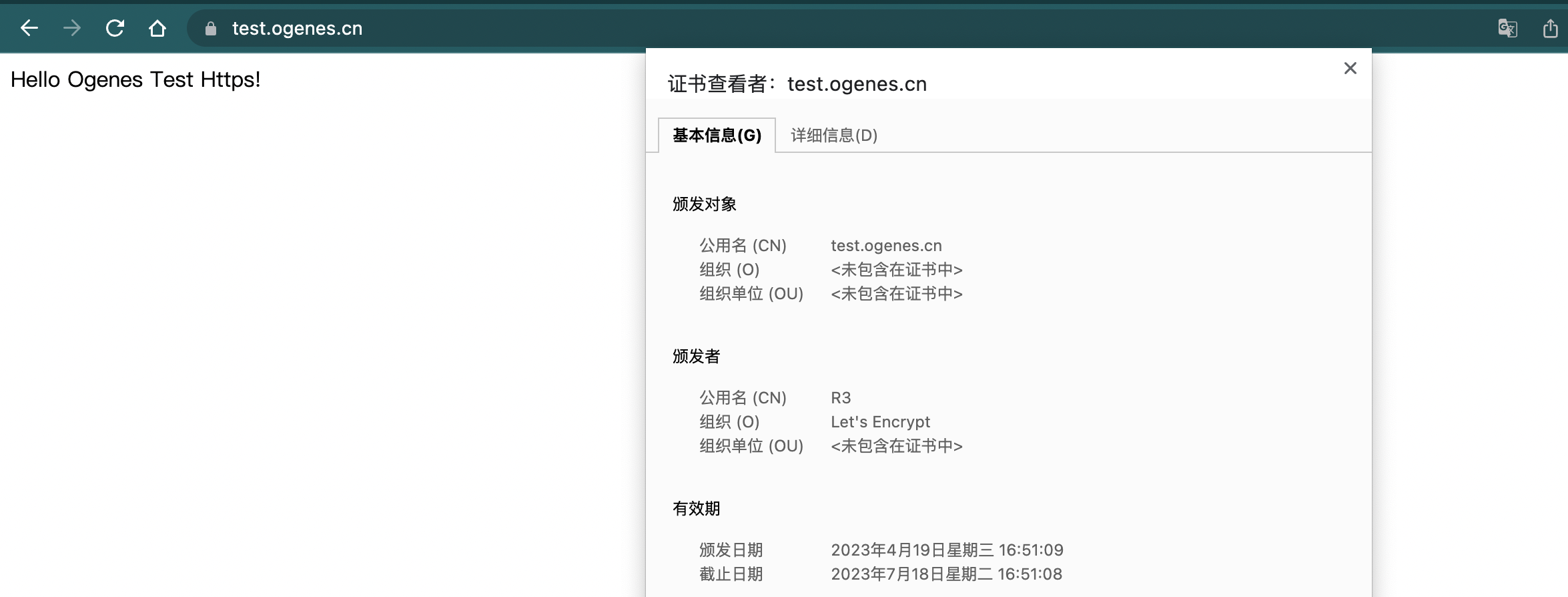
Docker-compose 启动 lnmp 开发环境
GitHub传送阵 docker-lnmp 项目帮助开发者快速构建本地开发环境,包括Nginx、PHP、MySQL、Redis 服务镜像,支持配置文件和日志文件映射,不限操作系统;此项目适合个人开发者本机部署,可以快速切换服务版本满足学习服务新…...

《android源码阅读四》Android系统源码整编、单编并运行到虚拟机
1、编译环境 《安装Ubuntu系统》《android源码下载》 2、整编源码 进入Android源码根目录 cd AOSP初始化环境 source build/envsetup.sh清除缓存 make clobber选择编译目标 // 选择编译目标 lunch // 因为本次是在虚拟机中运行,这里使用x86 lunch aosp_x86_6…...

深度学习技巧应用8-各种数据类型的加载与处理,并输入神经网络进行训练
大家好,我是微学AI,今天给大家介绍一下深度学习技巧应用8-各种数据类型的加载与处理,并输入神经网络进行训练。在模型训练中,大家往往对各种的数据类型比较难下手,对于非结构化数据已经复杂的数据的要进行特殊处理,这里介绍一下我们如何进行数据处理才能输入到模型中,进…...

【笔试】备战秋招,每日一题|20230415携程研发岗笔试
前言 最近碰到一个专门制作大厂真题模拟题的网站 codefun2000,最近一直在上面刷题。今天来进行2023.04.15携程研发岗笔试,整理了一下自己的思路和代码。 比赛地址 A. 找到you 题意: 给定一个仅包含小写字母的 n n n\times n nn 的矩阵…...
【unity专题篇】—GUI(IMGUI)思维导图详解
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...

【C++ Metaprogramming】0. 在C++中实现类似C#的泛型类
两年前,笔者因为项目原因刚开始接触C,当时就在想,如果C有类似C#中的泛型限定就好了,能让代码简单许多。我也一度认为: 虽然C有模板类,但是却没办法实现C#中泛型特有的 where 关键词: public c…...
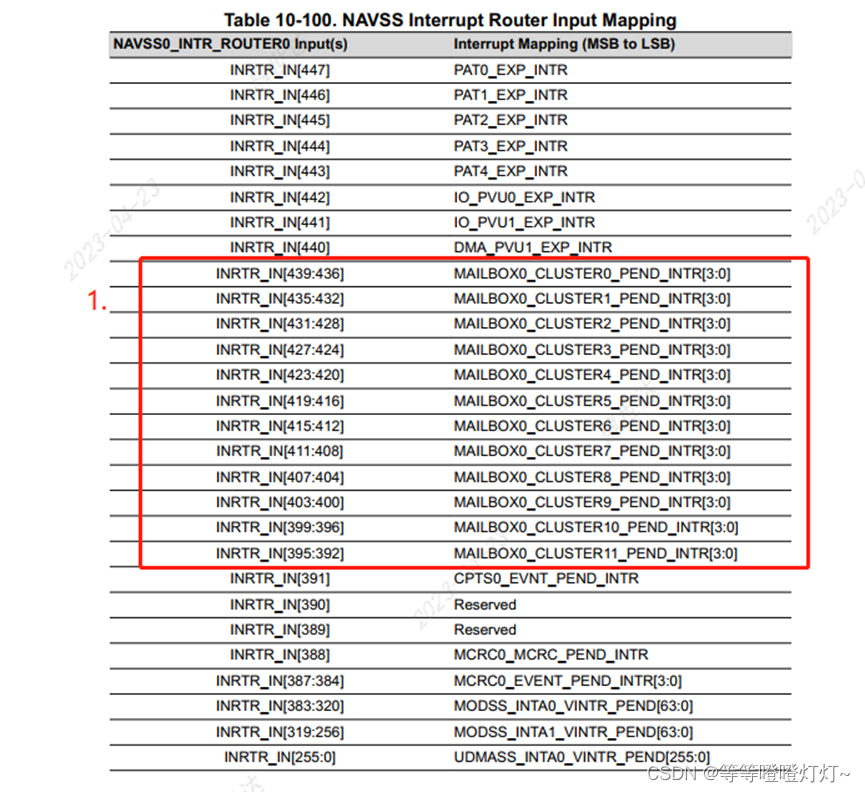
TDA4VM/VH 芯片 NAVSS0
请从官网下载 TD4VM 技术参考手册,地址如下: TDA4VM 技术参考手册地址 概述 (NAVSS0 的介绍在 TRM 的第10.2章节) NAVSS0 可以看作 MAIN 域的一个复杂外设域,实现如下功能: UDMASS: DMA 管理子系统;MODSS…...

基于springboot的前后端分离的案列(一)
SpringBootWeb案例 前面我们已经讲解了Web前端开发的基础知识,也讲解了Web后端开发的基础(HTTP协议、请求响应),并且也讲解了数据库MySQL,以及通过Mybatis框架如何来完成数据库的基本操作。 那接下来,我们就通过一个案例…...
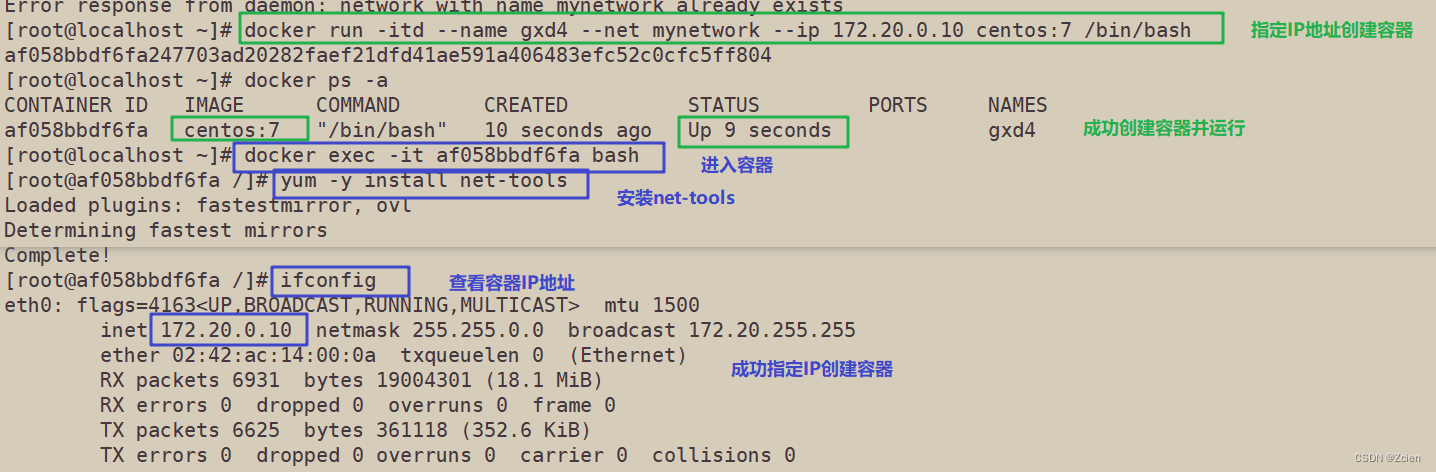
Docker网络模式详解
文章目录 一、docker网络概述1、docker网络实现的原理1.1 随机映射端口( 从32768开始)1.2 指定映射端口1.3 浏览器访问测试 二、 docker的网络模式1、默认网络2、使用docker run 创建Docker容器时,可以用--net或--network 选项指定容器的网络模式 三、docker网络模式…...
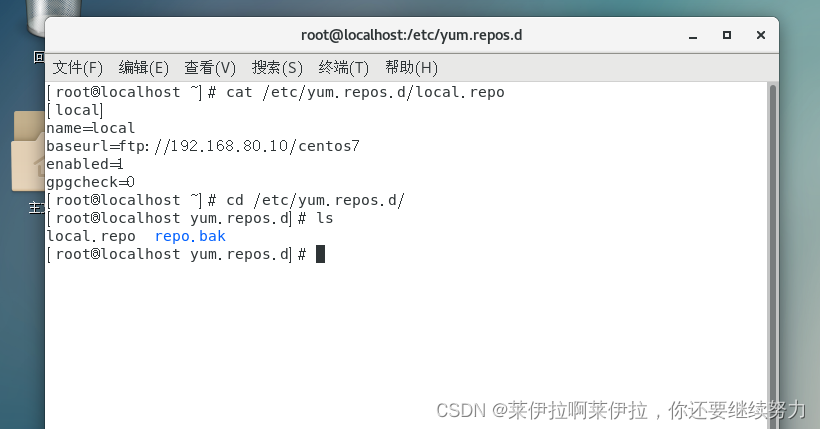
PXE高效批量网络装机
PXE 定义 PXE(预启动执行环境,在操作系统之前运行)是由Intel公司开发的网络引导技术,工作在client /server模式,允许客户机通过网络从远程服务器下载引导镜像,并加载安装文件或者整个操作系统。 具备以下三个优点 1 规模化: 同时…...

YOLOv5+双目实现三维跟踪(python)
YOLOv5双目实现三维跟踪(python) 1. 目标跟踪2. 测距模块2.1 测距原理2.2 添加测距 3. 细节修改(可忽略)4. 实验效果 相关链接 1. YOLOV5 双目测距(python) 2. YOLOV7 双目测距(python&#x…...

ESP8266使用SDK软硬件定时执行函数
1、软件定时 以下接口使用的定时器由软件实现,定时器的函数在任务中被执行。因为任务可能被中断,或者被其他高优先级的任务延迟,因此以下os_timer系列的接口并不能保证定时器精确执行。 注意: ①对于同一个 timer,os…...
ThreadPoolExecutor源码阅读流程图
1.创建线程池 public ThreadPoolExecutor(int corePoolSize,int maximumPoolSize,long keepAliveTime,TimeUnit unit,BlockingQueue<Runnable> workQueue) {this(corePoolSize, maximumPoolSize, keepAliveTime, unit, workQueue,Executors.defaultThreadFactory(), def…...

如何通过筛选高质量爬虫IP提升爬虫效率?
前言 对于做数据抓取的技术员来说,如何稳定高效的爬取数据ip库池起到决定性作用,对于爬虫ip池的维护,可以从以下几个方面入手: 目录 一、验证爬虫ip的可用性二、更新爬虫ip池三、维护爬虫ip的质量四、监控爬虫ip的使用情况 一、验…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
