阿里云国际版ACE与国内版ACE区别
1.国际版ACE与国内版ACE有哪些不同
2.国际版ACP/ACE约考流程
2.1 登录VUE官方网站约考
https://www.pearsonvue.com.cn/Clients/Alibaba-Cloud-Certification.aspx
2.2 如果之前有注册过账户,那就直接登录,如果还没有账户,那就创建账户
2.3 登录后,要约考,点 查看考试
2.4 下面以约考ACE为例,点了查看考试,选择ACE方向,会出现下面的界面
at a test center,指的是去考点考试,不方便
OnVUE指的是,在线上考试,我们选这个,注意:VUE在大陆区域不支持线上考试,没关系,我们可以安排
2.5 继续下一步,需要全部同意,才能下一步,全部勾选,点同意,到这个界面,这里要注意时区
2.6 你选择一个合适的时间点,确认,再次确认下考试科目/考试日期/考试时间没有选错,然后点付款
2.7 这里输入考试券,不要在官网直接购买,贵,加最底下微信,有考试券,能优惠点
2.8 会再和你确认下,个人信息/考试安排,确实无误,点提交订单
3.国际版ACE考试过程
因为要求提前半小时check in,请注意:
考试前45分钟就要就位
考试前将电脑重启
用个人的电脑,家庭网络环境。最好别用公司电脑,公司网络环境,怕有些安全策略,连不上考试服务器
准备好护照,驾照或者身份证
有条件,可以准备个梯子,万一连不上考试服务器,搭梯子
点check in后,会出现一个access code,记住这个access code,用笔写下来,怕中途出现什么状况,用这个access code重新进,可以省去很多重复步骤
3.1.还是登录VUE官方网站
https://home.pearsonvue.com/alibaba
考试前半小时,会在你预定的考试下面出现一个 CHECK IN 按钮,点check in,会有下面几个步骤
再次检测考试环境
需要你上传你的证件照片(护照,身份证或者驾照),以及考试位置的前后左右四个方位的照片,您可以选择用你的手机扫描页面所显示的二维码,在手机上上传;也可以用考试电脑拍摄并上传
会有个印度老师跟你对话或者文字聊天,说英语,大概要求你:
a)用考试电脑拍一下考试位置的照片,要求考试桌面上没有杂物,纸张,书籍以及耳机;
b)手机放到你够不着的地方
进入考试,前几分钟是测试,你就直接next下去就好,然后正式出来考题了
3.2.提交试卷后,立即可以看到你的成绩
可以在这个页面下看到你的成绩
https://wsr.pearsonvue.com/testtaker/registration/ViewScoreReports.htm?sortExamsColumn=examCompletedDateTime&sortExamsAscending=false&previousSortExamsColumn=&conversationId=445425
3.3.去阿里云国际站绑定VUE账号领证
相关文章:

阿里云国际版ACE与国内版ACE区别
1.国际版ACE与国内版ACE有哪些不同 2.国际版ACP/ACE约考流程 2.1 登录VUE官方网站约考 https://www.pearsonvue.com.cn/Clients/Alibaba-Cloud-Certification.aspx 2.2 如果之前有注册过账户,那就直接登录,如果还没有账户,那就创建账户 2.…...

Mysql8.0 gis支持
GIS数据类型 MySQL的GIS功能遵守OGC的OpenGIS Geometry Model,支持其定义的空间数据类型的一个子集,包括以下空间数据类型: GEOMETRY:不可实例化的数据类型,但是可以作为一个列的类型,存储任何一种其他类型的数据POIN…...

汇编---Nasm
文章目录 比较流行的汇编语言有3种:不同风格的汇编语言在语法格式上会有不同: 实战代码:Intrinsic函数手写汇编(8086汇编)调用C的API库函数调用约定实际代码 C调用汇编函数进行计算纯C实现如下:CASM实现:纯ASM实现:ASM打印命令行参…...
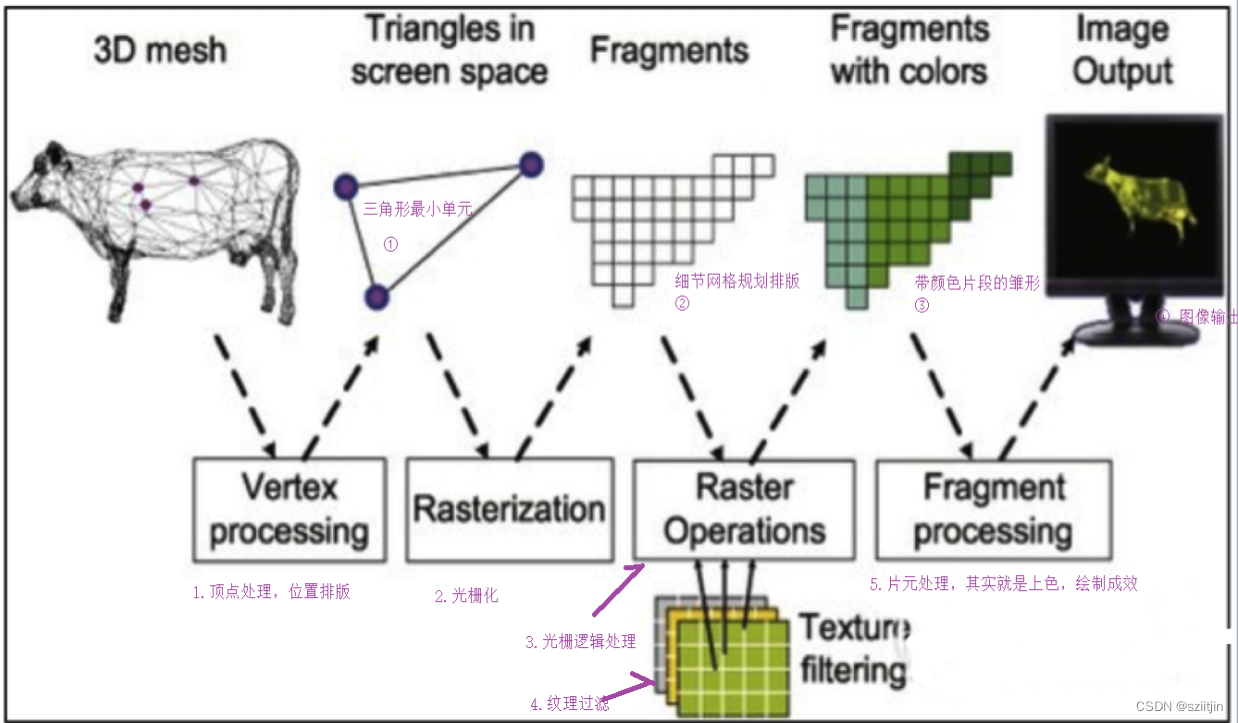
NDK OpenGL渲染画面效果
NDK系列之OpenGL渲染画面效果技术实战,本节主要是通过OpenGL Java库(谷歌对OpenGL C库做了JIN封装,核心实现还是在Native层),实现页面渲染,自定义渲染特效。 实现效果: 实现逻辑: 1…...

常见的深度学习框架
框架优点缺点TensorFlow- 由Google开发和维护,社区庞大,学习资源丰富- 具备优秀的性能表现,支持大规模分布式计算- 支持多种编程语言接口,易于使用- 提供了可视化工具TensorBoard,可用于调试和可视化模型- 底层架构复杂…...
【设计模式】七大设计原则--------单一职责原则
文章目录 1.案例1.1 原始案例1.2 改进一:类上遵循单一职责原则1.3 改进二:方法上遵循单一职责原则 2.小结 1.案例 1.1 原始案例 package com.sdnu.principle.singleresponsibility; //客户端 public class singleResponsibility {public static void m…...

MySQL-中间件mycat(一)
目录 🍁mycat基础概念 🍁Mycat安装部署 🍃初始环境 🍃测试环境 🍃下载安装 🍃修改配置文件 🍃启动mycat 🍃测试连接 🦐博客主页:大虾好吃吗的博客 ǹ…...
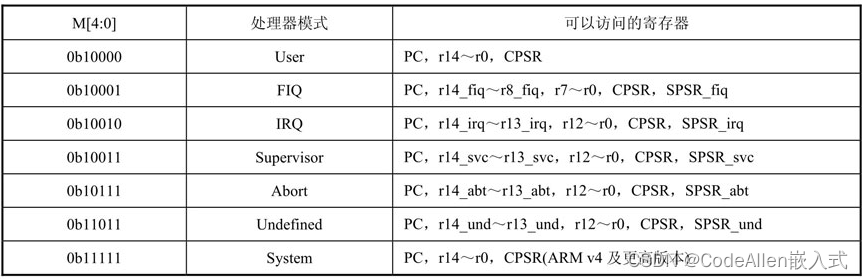
ARM寄存器组织
ARM有37个32位长的寄存器: 1个用做PC(Program Counter); 1个用做CPSR(Current Program Status Register); 5个用做SPSR(Saved Program Status Registers); 30个通用寄存器。 AR…...

记录一次webdav协议磁盘挂载经验总结
记录一次磁盘挂载经验总结 文章目录 记录一次磁盘挂载经验总结适配环境服务器协议适配方案脚本与详细说明 适配环境 windows 11windows 10windows 7 x86 and x64linuxuos统信国产化linux系统 服务器协议 webdav 适配方案 一、通用 winfsprclone 已验证通过,版…...

安装Django
1. 在物理环境安装Django Python官方的PyPi仓库为我们提供了一个统一的代码托管仓库,所有的第三方库,甚至你自己写的开源模块,都可以发布到这里,让全世界的人分享下载 pip是最有名的Python包管理工具 。提供了对Python包的查找、…...

【前端面经】JS-如何使用 JavaScript 来判断用户设备类型?
在 Web 开发中,有时需要针对不同的设备类型进行不同的处理。例如,对于移动设备,我们可能需要采用不同的布局或者交互方式,以提供更好的用户体验。因此,如何判断用户设备类型成为了一个重要的问题。 1. 使用 navigator…...
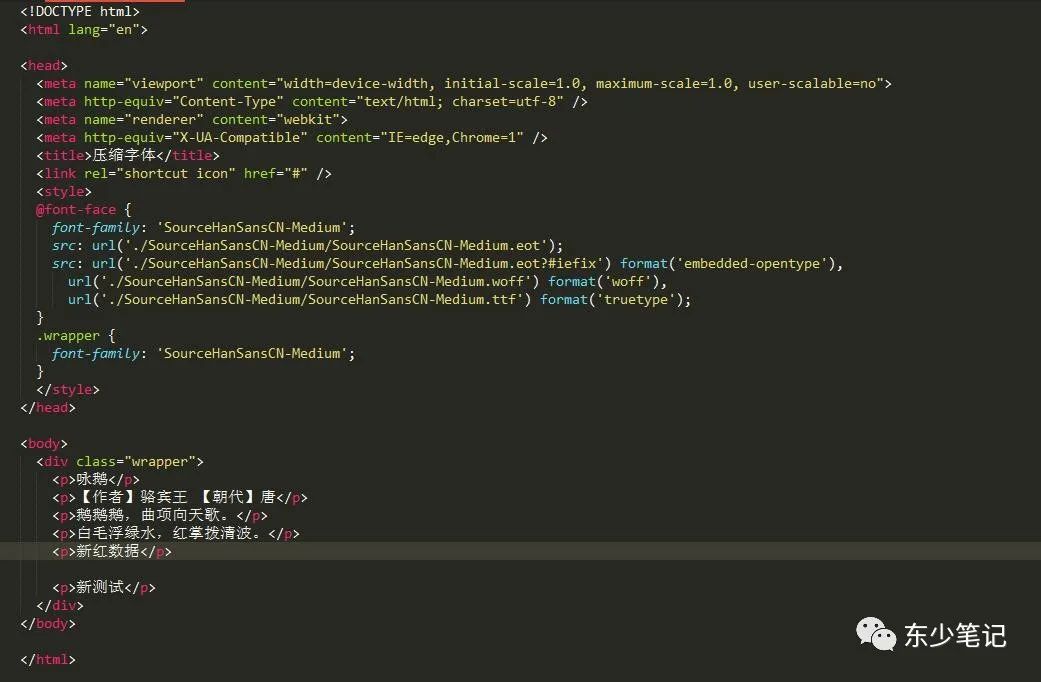
压缩HTML引用字体
内容简介 有些网站为了凸显某部分字体,而引入自定义字体,但由于自定义字体相对都比较大(几M),导致页面加载缓慢;所以本文介绍三种压缩字体的方法,可根据项目情况自行选择。 压缩方法 1、利用Fontmin程序&a…...
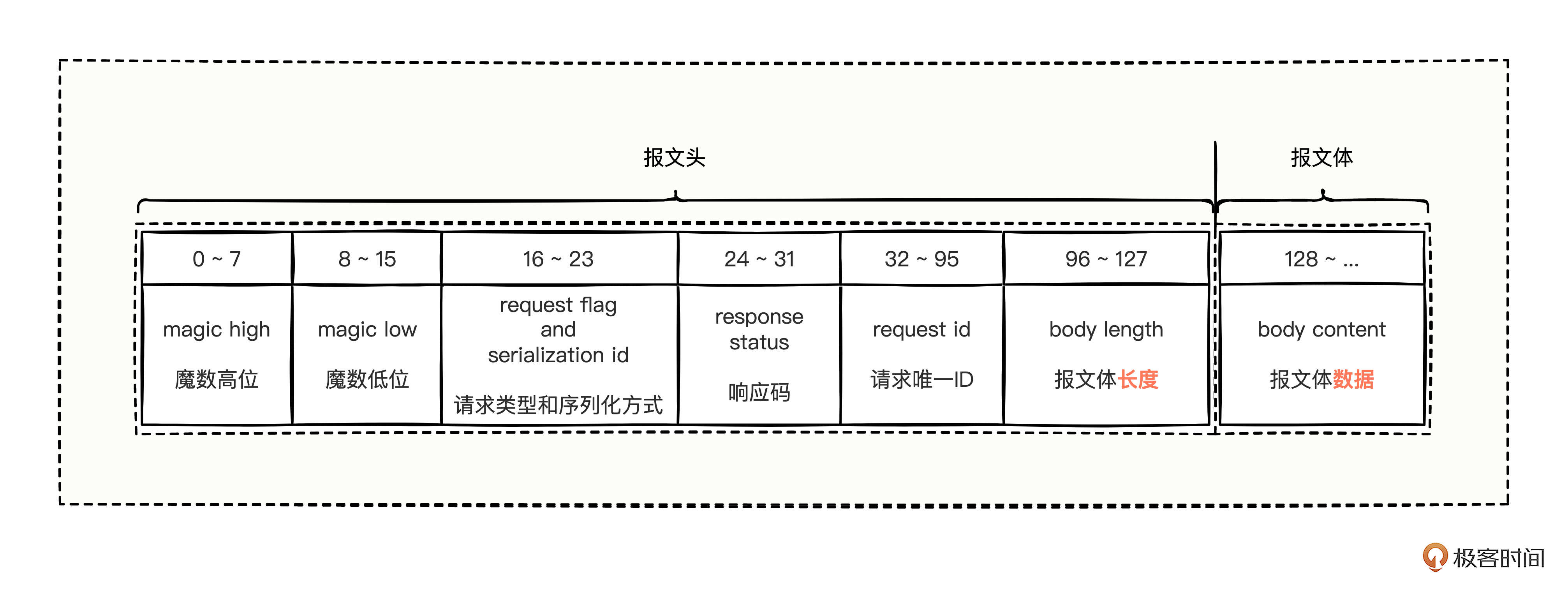
大厂高频面试:底层的源码逻辑知多少?
你好,我是何辉。今天我们来聊一聊Dubbo的大厂高频面试题。 大厂面试,一般重点考察对技术理解的深度,和中小厂的区别在于,不仅要你精于实战,还要你深懂原理,勤于思考并针对功能进行合理的设计。 网上一直流…...

【学习笔记】CF607E Cross Sum
最后一道数据结构,不能再多了。 而且需要一点计算几何的知识,有点难搞。 分为两个部分求解。 首先考虑找到距离 ≤ r \le r ≤r的交点数量。发现这等价于圆上两段圆弧相交,因此将圆上的点离散化后排序,用一个主席树来求就做完了…...

Python 一元线性回归模型预测实验完整版
一元线性回归预测模型 实验目的 通过一元线性回归预测模型,掌握预测模型的建立和应用方法,了解线性回归模型的基本原理 实验内容 一元线性回归预测模型 实验步骤和过程 (1)第一步:学习一元线性回归预测模型相关知识。 线性回归模型属于…...

GStreamer第一阶段的简单总结
这里写目录标题 前言个人的总结v4l2src插件的简单使用 前言 因为涉及很多细节的GStreamer官方论坛有详细解链接: GStreamer官网,这里不做说明,以下只是涉及到个人的理解和认知,方便后续的查阅。 个人的总结 1)了解pipeline的使用࿰…...

【网络进阶】服务器模型Reactor与Proactor
文章目录 1. Reactor模型2. Proactor模型3. 同步IO模拟Proactor模型 在高并发编程和网络连接的消息处理中,通常可分为两个阶段:等待消息就绪和消息处理。当使用默认的阻塞套接字时(例如每个线程专门处理一个连接),这两…...

使用div替代<frameset><frame>的问题以及解决办法
首先是原版三层框架的html: <html> <head> <title>THPWP</title> </head> <!-- 切记frameset不能写在body里面,以下代表首页由三层模块组成,其中第一层我是用来放菜单高度占比14%,中间的用作主…...

Verilog中的`define与`if的使用
一部分代码可能有时候用,有时候不用,为了避免全部编译占用资源,可以使用条件编译语句。 语法 // Style #1: Only single ifdef ifdef <FLAG>// Statements endif// Style #2: ifdef with else part ifdef <FLAG>// Statements …...

沃尔玛、亚马逊影响listing的转化率4大因素,测评补单自养号解析
1、listing的相关性:前期我们在找词,收集词的时候,我们通过插件来协助我们去筛选词。我们把流量高,中,低的关键词都一一收集,然后我们再进行对收集得来的关键词进行分析,再进行挑词,…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
