Linux安装helm
前言
运行环境:CentOS7.9
官方参考文档:官方文档
文章末尾附有一键安装脚本
下载安装包
github下载对应版本的安装包,下载地址
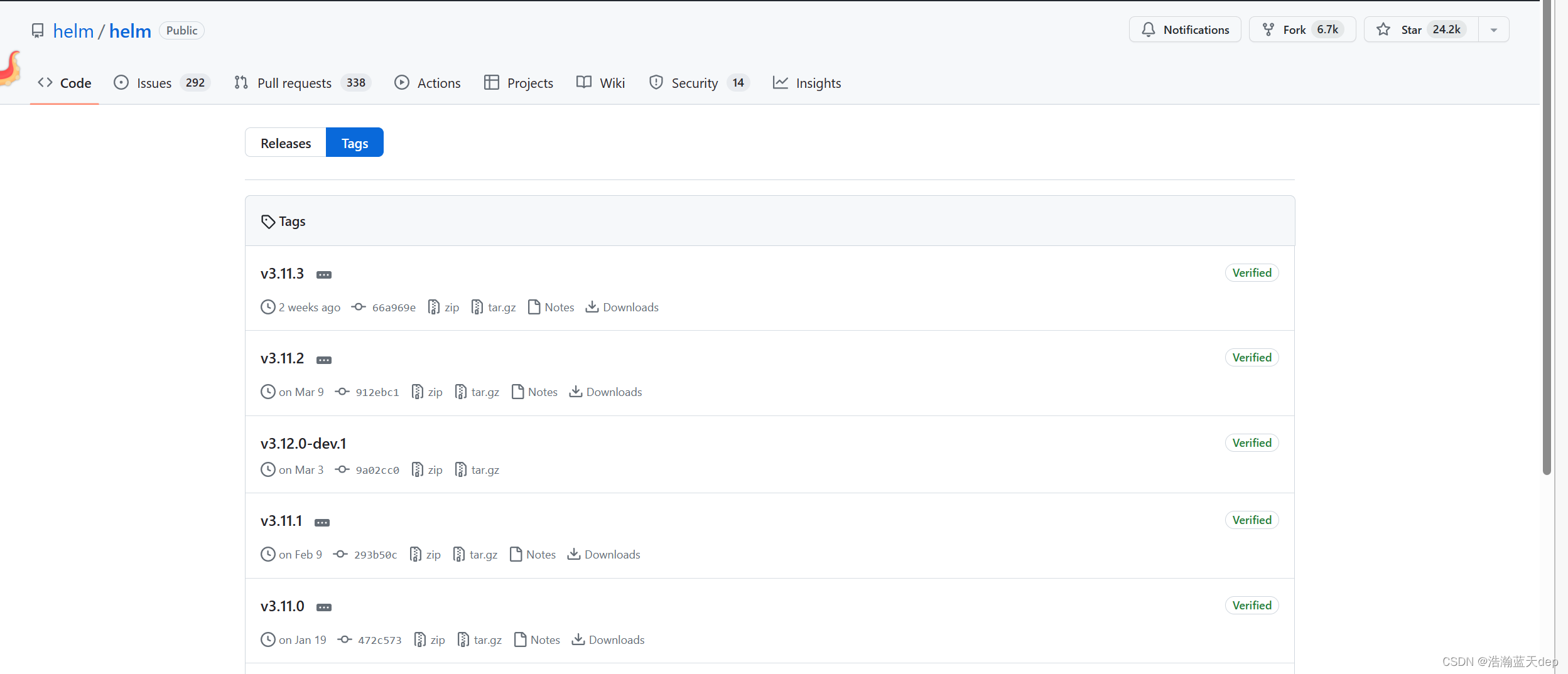
进入对应版本的下载页面,这里以v3.11.3为例
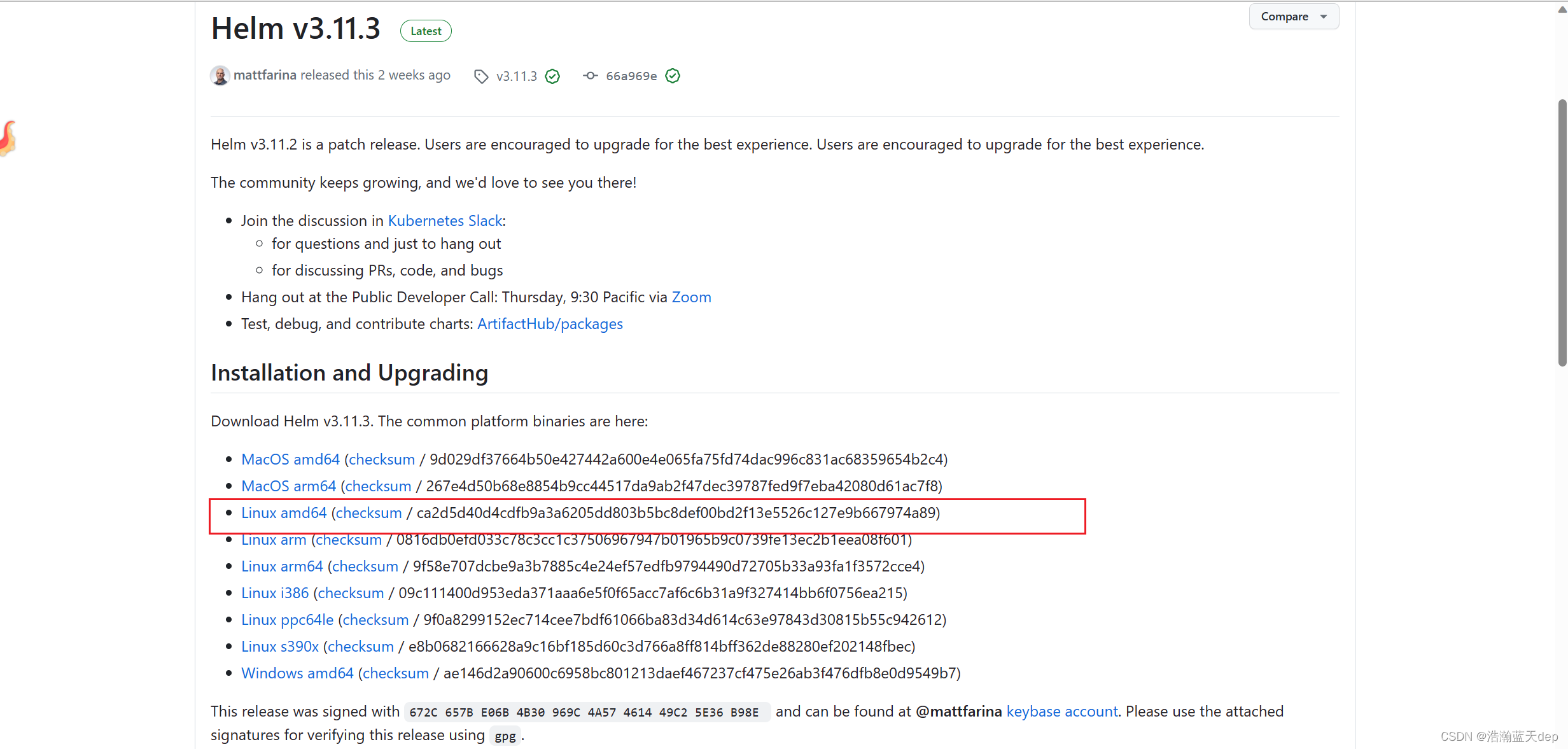
选择对应系统的安装包,这里以linux为例 ,复制下载地址

在linux系统中执行以下命令,下载安装包,下载路径替换为自己复制的路径即可
wget https://get.helm.sh/helm-v3.11.3-linux-amd64.tar.gz下载成功后会在当前路径下看到对应版本的文件

解压安装包
使用以下命令解压安装包,-C参数可以不写,如果不写的话默认解压到当前所在的目录
tar -zxvf helm-v3.11.3-linux-amd64.tar.gz -C ./server/
解压成功后会在对应的目录中看到一个linux-amd64的目录
目录中最主要的就是helm这个文件

安装配置
将helm文件移动到/usr/local/bin/下面或者配置当前文件所在路径的环境变量都可以,下面会把两种方法都说一下,以下方式二选一即可
第一种:配置环境变量
将helm所在的目录配置到环境变量中。编辑/etc/profileprofile文件或者在/etc/profile.d/下面新建一个专门用于配置环境变量的文件也行,博主喜欢自己新建个文件,方便统一管理所有安装的软件的环境变量
vim /etc/profile.d/my_env.sh 在文件末尾追加以下内容
# helm配置
HELM_HOME=/root/server/linux-amd64
export PATH=$HELM_HOME:$PATH保存文件退出后刷新境变量
source /etc/profile第二种:移动文件到/usr/local/bin
使用以下命令将helm文件移动下/usr/local/bin下面即可
mv linux-amd64/helm /usr/local/bin/验证是否成功
使用以下命令进行验证
helm version打印以下内容代表安装成功

一键安装脚本
参数说明
$1: 必填参数,安装包的下载路径
$2: 可选参数,文件安装的位置,如果不传默认在当前目录中
#!/bin/bashdownload_path=$1
install_path=`pwd`if [ -z $1 ];thenecho "请输入下载地址"return
fiif [ -n "$2" ];theninstall_path=$(cd $2 && pwd)
fiinstall_name=helm-linux-amd64.tar.gz# 下载安装包
wget -O $install_name $download_path# 解压
tar -zxvf $install_name -C $install_path# 安装
if [ -z $2 ];thenmv $install_path/linux-amd64/helm /usr/local/bin/helm# 删除解压的文件夹rm -rf $install_path/linux-amd64/
else# 添加环境变量echo -e "\n# helm配置" >> /etc/profile.d/my_env.shecho "HELM_HOME=$install_path/linux-amd64" >> /etc/profile.d/my_env.shecho "export PATH=\$HELM_HOME:\$PATH" >> /etc/profile.d/my_env.sh# 刷新环境变量source /etc/profile
fi# 校验是否安装成功
helm versionif [ $? != 0 ];thenecho "helm install failed"
fi# 移除下载的安装包
rm -f $install_name使用以下命令运行安装包
source <脚本名称> <下载地址> <安装路径>示例
source helm_install.sh https://get.helm.sh/helm-v3.11.3-linux-amd64.tar.gz结束
以上便是linux安装helm的全部过程,如有问题欢迎随时交流
相关文章:

Linux安装helm
前言 运行环境:CentOS7.9 官方参考文档:官方文档 文章末尾附有一键安装脚本 下载安装包 github下载对应版本的安装包,下载地址 进入对应版本的下载页面,这里以v3.11.3为例 选择对应系统的安装包,这里以linux为例 …...
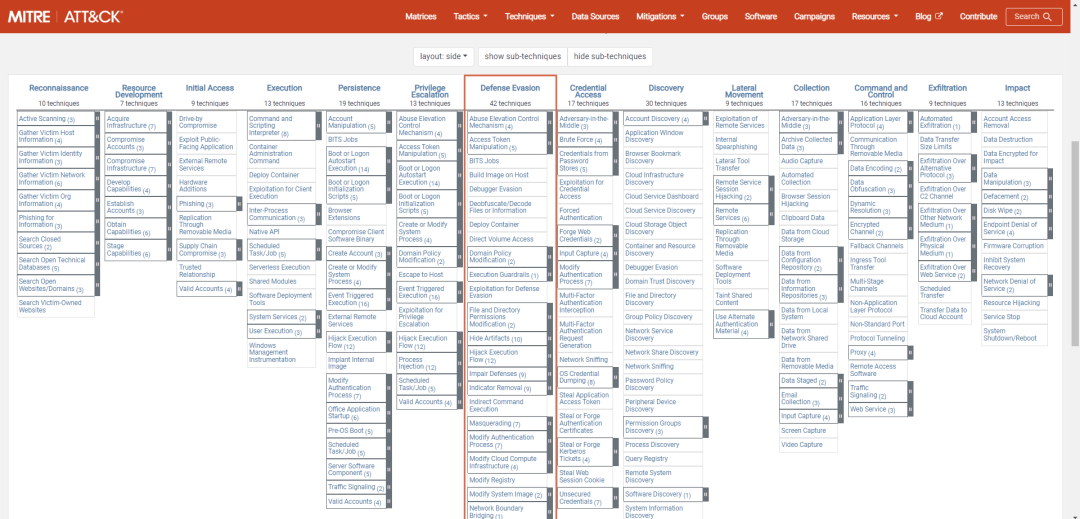
ATTCK v12版本战术介绍——防御规避(四)
一、引言 在前几期文章中我们介绍了ATT&CK中侦察、资源开发、初始访问、执行、持久化、提权战术理论知识及实战研究、部分防御规避战术,本期我们为大家介绍ATT&CK 14项战术中防御规避战术第19-24种子技术,后续会介绍防御规避其他子技术…...
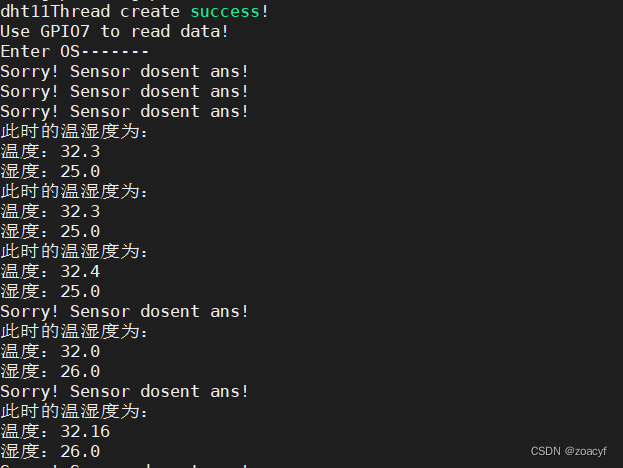
Orangepi Zero2 全志H616(DHT11温湿度检测)
最近在学习Linux应用和安卓开发过程中,打算把Linux实现的温湿度显示安卓app上,于是在此之前先基于Orangepi Zero2 全志H616下的wiringPi库对DHT11进行开发,本文主要记录开发过程的一些问题和细节,主要简单通过开启线程来接收温湿度…...
abbyy是什么软件
ABBYY,一款强大的OCR文字识别软件! 在日常的工作中,我们常常需要提取PDF或图片上的大段文字,如果字数少的话,我们可以直接手打,但如果出现大篇幅的文字,那就有点头疼了。今天,我就向…...

软件测试技术(四)白盒测试
白盒测试 白盒测试(White Box Testing)又称结构测试、透明盒测试、逻辑驱动测试或基于代码的测试。白盒测试只测试软件产品的内部结构和处理过程,而不测试软件产品的功能,用于纠正软件系统在描述、表示和规格上的错误,…...
:try-catch块)
Java基础语法(十二):try-catch块
目录 前言 一、try-catch是什么? 二、其他异常处理机制 总结 前言 Java 异常处理机制是 Java 程序设计中至关重要的一部分。它允许程序员像处理普通数据一样处理异常,并根据异常类型采取合适的措施。其中一个非常基本的异常处理机制是 try-catch 块…...
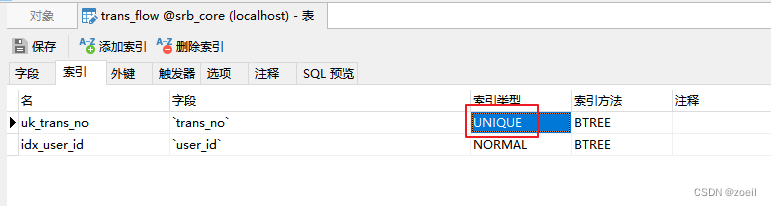
尚融宝25-投资列表展示以及实现充值功能
目录 一、展示投资列表 (一)需求 (二)后端 (三)前端 二、充值功能 (一)需求 1、需求描述 2、流程 (二)充值 1、后端 2、前端 (三&…...

QML基础模型(Basic Model)
最基本的分离数据与显示的方法是使用Repeater元素。它被用于实例化一组元素项,并且很容易与一个用于填充用户界面的定位器相结合。 最基本的实现举例,repeater元素用于实现子元素的标号。每个子元素都拥有一个可以访问的属性index,用于区分不…...

如果ChatGPT写作论文,保姆及教程以及问题答疑
上次发表“如何用ChatGPT完成论文”后,许多捧场看官评论讨论,也有不少同学实操成功,但更多人寻求帮助。所以今天再整理一篇,把大家的疑问进行说明。 1. ChatGPT写的论文能否被检查出? 有同学反映将一段ChatGPT…...

机器人中的数值优化(三)—— 无约束最优化方法基础、线搜索准则
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...
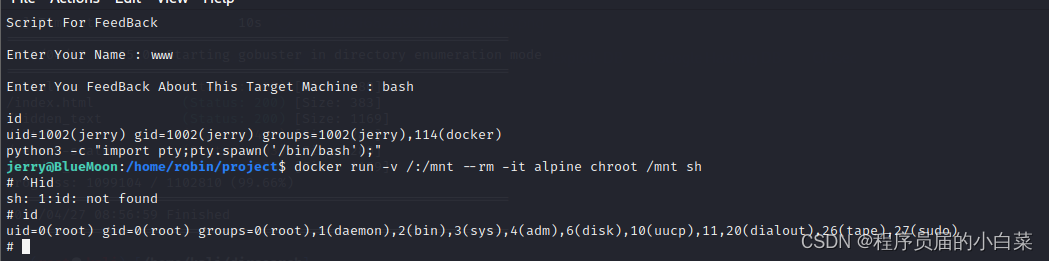
vulnhub靶场之bluemoon
1.信息收集 存活主机进行探测,发现主机192.168.239.176存活。 对主机192.168.239.176进行端口扫描,发现21、22、80端口 访问http://192.168.239.176,并查看源码未发现可利用的行为。 进行目录扫描发现可疑路径/hidden_text 浏览器访问h…...
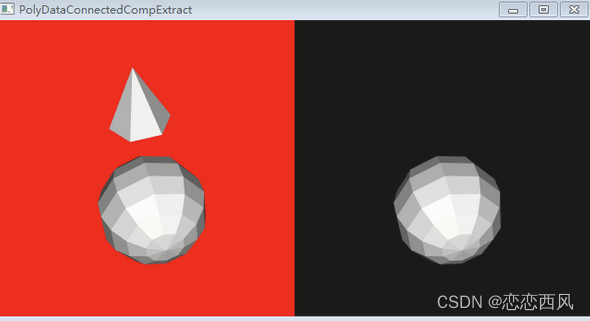
VTK 几何体连通区域分析 vtkPolyDataConnectivityFilter
前言: vtkPolyDataConnectivityFilter 使用过,但网上没有看到完事的教程;这里整理一下; 提取数据集中连通的多边形数据。 该类是一个滤波器,提取cell(区域) - 拥有公共点或者满足某个阈值 该类…...
scss、css样式中使用变量的方法;Vue动态改变css等样式文件中的变量
目录 一、问题 二、原因及解决方法 三、总结 一、问题 1.遇到一些样式 设置的值都是重复的不想重复写,想和js一样定义一个常量,然后直接引用这个常量。 2.想要在js中动态设置样式中的值,在 css、scss等样式表中直接使用。 二、原因及解…...

数据治理在学术上的发展史以及未来展望
数据治理是大数据领域中非常重要的一环,从早期的学术研究到如今的各大企业落地实践,经历了漫长的过程,数据治理的实践落地本身也是一场马拉松。 从百度学术通过精确关键词匹配,搜索中文期刊的“数据治理” 和外文期刊的“data gov…...
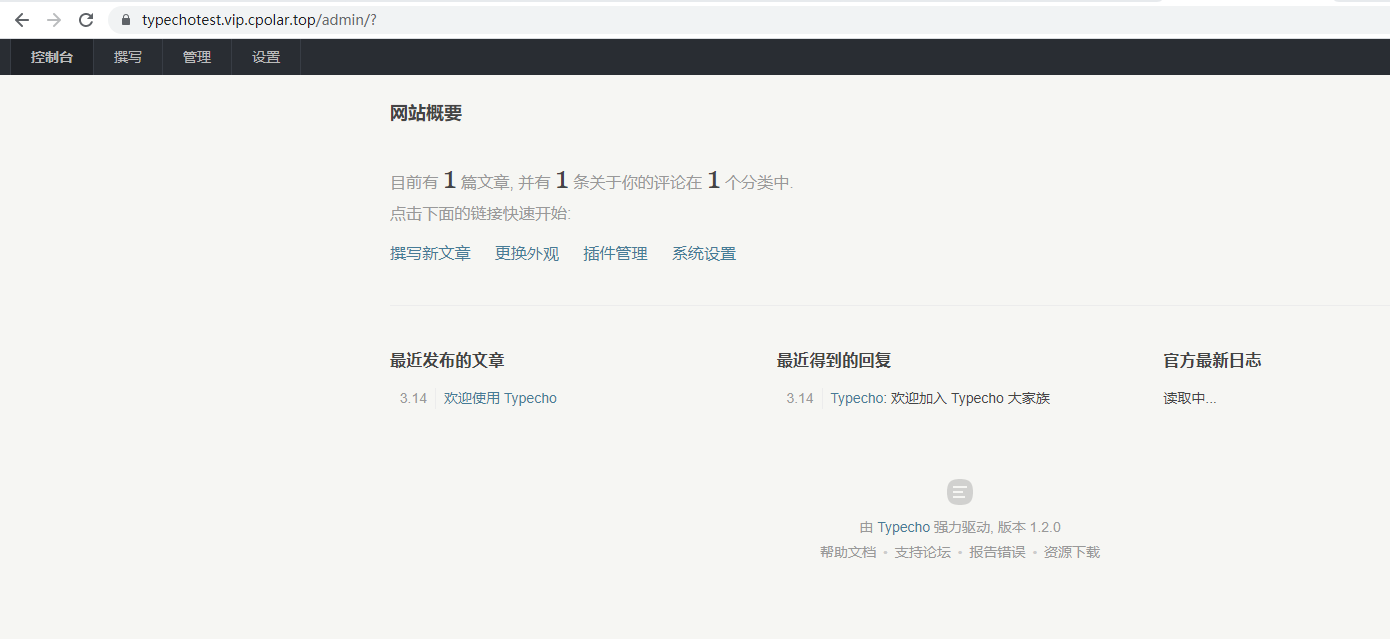
【搭建博客】宝塔面板部署Typecho博客,并发布上线访问
目录 前言 1.安装环境 2.下载Typecho 3.创建站点 4.访问Typecho 5.安装cpolar 6.远程访问Typecho 7.固定远程访问地址 8.配置typecho 前言 Typecho是由type和echo两个词合成的,来自于开发团队的头脑风暴。Typecho基于PHP5开发,支持多种数据库&…...
【Spring篇】IOC相关内容
🍓系列专栏:Spring系列专栏 🍉个人主页:个人主页 目录 一、bean基础配置 1.bean基础配置(id与class) 2.bean的name属性 3.bean作用范围scope配置 二、bean实例化 1.构造方法实例化 2.分析Spring的错误信息 3.静态工厂实例化 4.实例工厂 5.FactoryBean 三…...

Python超矩形
文章目录 距离函数矩形分割 Rectangle是 scipy.spatial中封装的类,其构造函数只需输入最小值和最大值的数组即可,并且可通过内置的 volume方法计算广义的体积。 from scipy.spatial import Rectanglerec Rectangle((0,0), (5,5)) print(rec.maxes) …...
【软考数据库】第五章 计算机网络
目录 5.1 网络功能和分类 5.2 OSI七层模型 5.3 TCP/IP协议 5.4 传输介质 5.5 通信方式和交换方式 5.6 IP地址 5.7 IPv6 5.8 网络规划和设计 5.9 其他考点补充 5.10 网络安全技术 5.11 网络安全协议 前言: 笔记来自《文老师软考数据库》教材精讲ÿ…...

深眸科技|深度学习、3D视觉融入机器视觉系统,实现生产数智化
随着“中国制造2025”战略加速落实,制造业生产线正在加紧向智能化、自动化和数字化转型之路迈进。而人工智能技术的兴起以及边缘算力持续提升的同时,机器视觉及其相关技术也在飞速发展,并不断渗透进工业领域,拓展应用场景的同时&a…...

DateFormat使用时需要注意:多线程下需要特殊处理
前言 工作或学习过程中难免会接触到时间(Date)相关的内容,比如String类型转为Date类型,或者Date类型转为String类型,jdk为我们提供了一套完善的日期格式化工具,DateFormat类,使用者可以使用该接…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
