每天一道算法练习题--Day15 第一章 --算法专题 --- -----------二叉树的遍历
概述
二叉树作为一个基础的数据结构,遍历算法作为一个基础的算法,两者结合当然是经典的组合了。很多题目都会有 ta 的身影,有直接问二叉树的遍历的,有间接问的。比如要你找到树中满足条件的节点,就是间接考察树的遍历,因为你要找到树中满足条件的点,就需要进行遍历。
你如果掌握了二叉树的遍历,那么也许其他复杂的树对于你来说也并不遥远了
二叉数的遍历主要有前中后遍历和层次遍历。 前中后属于 DFS,层次遍历则可以使用 BFS 或者 DFS 来实现。只不过使用 BFS 来实现层次遍历会容易些,因为层次遍历就是 BFS 的副产物啊,你可以将层次遍历看成没有提前终止的 BFS。
DFS 和 BFS 都有着自己的应用,比如 leetcode 301 号问题和 609 号问题。
DFS 都可以使用栈来简化操作,并且其实树本身是一种递归的数据结构,因此递归和栈对于 DFS 来说是两个关键点。
DFS 图解:
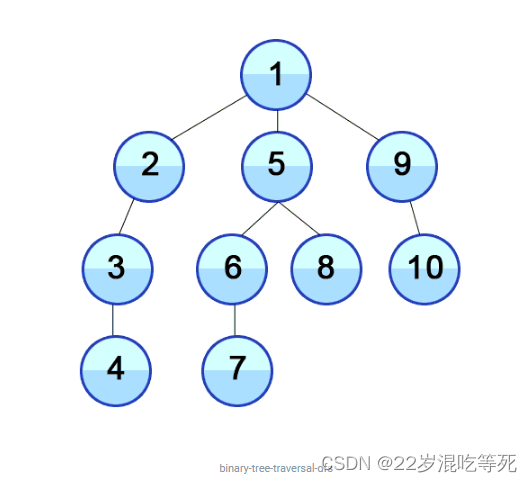
BFS 的关键点在于如何记录每一层次是否遍历完成, 我们可以用一个标识位来表式当前层的结束。
对于前中后序遍历来说。首先不管是前中还是后序遍历,变的只是根节点的位置, 左右节点的顺序永远是先左后右。 比如前序遍历就是根在前面,即根左右。中序就是根在中间,即左根右。后序就是根在后面,即左右根。
下面我们依次讲解:
前序遍历
相关问题144.binary-tree-preorder-traversal
前序遍历的顺序是根-左-右
思路是:
- 先将根结点入栈
- 出栈一个元素,将右节点和左节点依次入栈
- 重复 2 的步骤
总结: 典型的递归数据结构,典型的用栈来简化操作的算法。
其实从宏观上表现为:自顶向下依次访问左侧链,然后自底向上依次访问右侧链,如果从这个角度出发去写的话,算法就不一样了。从上向下我们可以直接递归访问即可,从下向上我们只需要借助栈也可以轻易做到。
整个过程大概是这样:
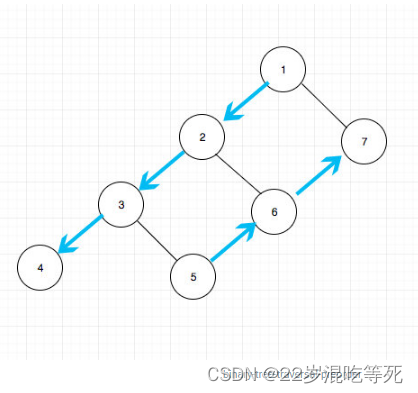
这种思路有一个好处就是可以统一三种遍历的思路. 这个很重要,如果不了解的朋友,希望能够记住这一点。
中序遍历
相关问题94.binary-tree-inorder-traversal
中序遍历的顺序是 左-根-右,根节点不是先输出,这就有一点点复杂了。
- 根节点入栈
- 判断有没有左节点,如果有,则入栈,直到叶子节点
此时栈中保存的就是所有的左节点和根节点。
- 出栈,判断有没有右节点,有则入栈,继续执行 2
值得注意的是,中序遍历一个二叉查找树(BST)的结果是一个有序数组,利用这个性质有些题目可以得到简化, 比如230.kth-smallest-element-in-a-bst, 以及98.validate-binary-search-tree
后序遍历
相关问题145.binary-tree-postorder-traversal
后序遍历的顺序是 左-右-根
这个就有点难度了,要不也不会是 leetcode 困难的 难度啊。
其实这个也是属于根节点先不输出,并且根节点是最后输出。 这里可以采用一种讨巧的做法, 就是记录当前节点状态,如果:
- 当前节点是叶子节点或者
- 当前节点的左右子树都已经遍历过了,那么就可以出栈了。
对于 1. 当前节点是叶子节点或者当前节点的左右子树都已经遍历过了,那么就可以出栈了。
对于 2. 当前节点的左右子树都已经遍历过了, 只需要用一个变量记录即可。最坏的情况,我们记录每一个节点的访问状况就好了,空间复杂度 O(n) 但是仔细想一下,我们使用了栈的结构,从叶子节点开始输出,我们记录一个当前出栈的元素就好了,空间复杂度 O(1), 具体请查看上方链接。
层次遍历
层次遍历的关键点在于如何记录每一层次是否遍历完成, 我们可以用一个标识位来表式当前层的结束。
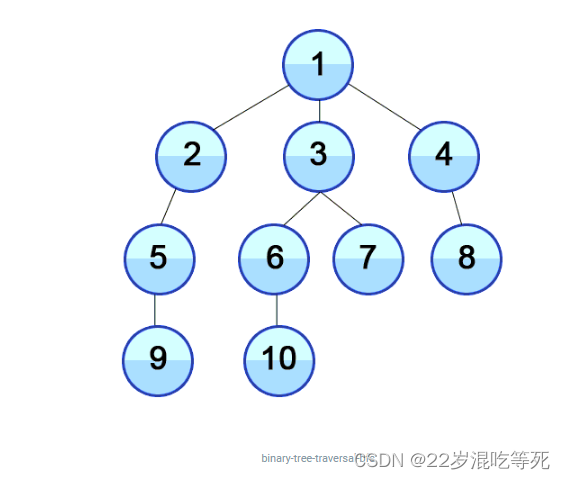
具体做法:
- 根节点入队列, 并入队列一个特殊的标识位,此处是 null
- 出队列
- 判断是不是 null, 如果是,则代表本层已经结束。我们再次判断是否当前队列为空,如果不为空继续入队一个 null,否则说明遍历已经完成,我们什么都不不用做
- 如果不为 null,说明这一层还没完,则将其左右子树依次入队列。
相关问题:

双色标记法
我们知道垃圾回收算法中,有一种算法叫三色标记法。 即:
- 用白色表示尚未访问
- 灰色表示尚未完全访问子节点
- 黑色表示子节点全部访问
那么我们可以模仿其思想,使用双色标记法来统一三种遍历。
其核心思想如下:
- 使用颜色标记节点的状态,新节点为白色,已访问的节点为灰色。
- 如果遇到的节点为白色,则将其标记为灰色,然后将其右子节点、自身、左子节点依次入栈。
- 如果遇到的节点为灰色,则将节点的值输出。
使用这种方法实现的中序遍历如下:
class Solution:def inorderTraversal(self, root: TreeNode) -> List[int]:WHITE, GRAY = 0, 1res = []stack = [(WHITE, root)]while stack:color, node = stack.pop()if node is None: continueif color == WHITE:stack.append((WHITE, node.right))stack.append((GRAY, node))stack.append((WHITE, node.left))else:res.append(node.val)return res
可以看出,实现上 WHITE 就表示的是递归中的第一次进入过程,Gray 则表示递归中的从叶子节点返回的过程。 因此这种迭代的写法更接近递归写法的本质。
如要实现前序、后序遍历,只需要调整左右子节点的入栈顺序即可。可以看出使用三色标记法, 其写法类似递归的形式,因此便于记忆和书写,缺点是使用了额外的内存空间。不过这个额外的空间是线性的,影响倒是不大。
虽然递归也是额外的线性时间,但是递归的栈开销还是比一个 0,1 变量开销大的。换句话说就是空间复杂度的常数项是不同的,这在一些情况下的差异还是蛮明显的。
划重点:双色迭代法是一种可以用迭代模拟递归的写法,其写法和递归非常相似,要比普通迭代简单地多。
Morris 遍历
我们可以使用一种叫做 Morris 遍历的方法,既不使用递归也不借助于栈。从而在 O ( 1 ) O(1) O(1) 空间完成这个过程。
如果你需要使用 O ( 1 ) O(1) O(1) 空间遍历一棵二叉树,那么就要使用 Morris 遍历。
这个算法考察相对少,作为了解即可。
def MorrisTraversal(root):curr = rootwhile curr:# If left child is null, print the# current node data. And, update# the current pointer to right child.if curr.left is None:print(curr.data, end= " ")curr = curr.rightelse:# Find the inorder predecessorprev = curr.leftwhile prev.right is not None and prev.right is not curr:prev = prev.right# If the right child of inorder# predecessor already points to# the current node, update the# current with it's right childif prev.right is curr:prev.right = Nonecurr = curr.right# else If right child doesn't point# to the current node, then print this# node's data and update the right child# pointer with the current node and update# the current with it's left childelse:print (curr.data, end=" ")prev.right = currcurr = curr.left
划重点:Morris 是一种可以在 O ( 1 ) O(1) O(1) 空间遍历二叉树的算法。
总结
本文详细讲解了二叉树的层次遍历和深度优先遍历。
对于深度优先遍历,我们又细分为前中后序三种遍历方式。
最后我们讲解了双色遍历和 Morris 遍历。这两种方式可以作为了解,不掌握也没关系。
另外,如果题目要求你实现迭代器(就是调用一次输出一个二叉树的值),那么前面讲的迭代的方式就非常适用了。比如这道题 Binary Search Tree Iterator
相关文章:

每天一道算法练习题--Day15 第一章 --算法专题 --- -----------二叉树的遍历
概述 二叉树作为一个基础的数据结构,遍历算法作为一个基础的算法,两者结合当然是经典的组合了。很多题目都会有 ta 的身影,有直接问二叉树的遍历的,有间接问的。比如要你找到树中满足条件的节点,就是间接考察树的遍历…...

golang - 函数的使用
核心化编程 为什么需要函数? 代码冗余问题不利于代码维护函数可以解决这个问题 函数 函数:为完成某一功能的程序指令(语句)的集合,称为函数 在 Go 中,函数分为:自定义函数(自己写…...

真题详解(极限编程)-软件设计(六十一)
真题详解(二分查找平均值)-软件设计(六十)https://blog.csdn.net/ke1ying/article/details/130417464 VLANtag属于 数据链路层实现。 数据链路层:网桥交换机。 网络层:路由器。 物理层:中继器。 Telent…...

计算机网络笔记:TCP粘包
默认情况下, TCP 连接会启⽤延迟传送算法 (Nagle 算法), 在数据发送之前缓存他们. 如果短时间有多个数据发送, 会缓冲到⼀起作⼀次发送 , 这样可以减少 IO 消耗提⾼性能。 如果是传输⽂件的话, 那么根本不⽤处理粘包的问题, 来⼀个包拼⼀个包就好了。但是如果是多条消息, 或者…...

Vue(标签属性:ref、配置项:props、混入mixin、插件、样式属性:scroped)
一、ref(打标识) 前面提及到了标签属性:keys 这里将了解ref:打标识 正常布置脚手架并创建入口文件main.js,引入组件 1. 可以给元素注册引用信息(获取真实DOM) 给一个按钮获取上方的dom的方法,方…...
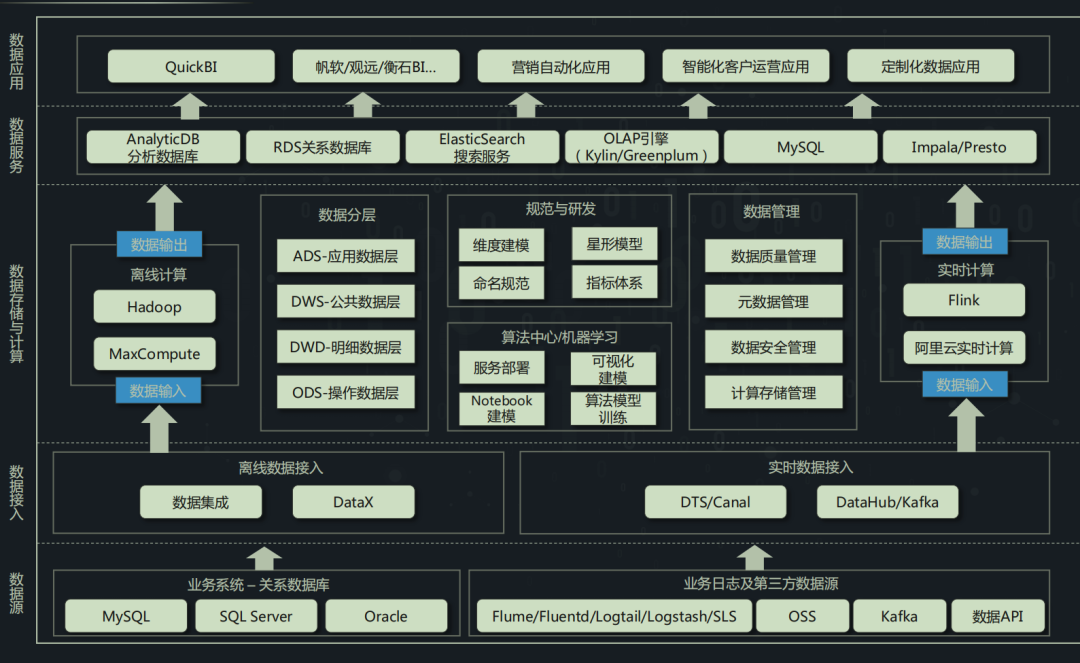
数仓建设规划核心问题!
小A进入一家网约车出现服务公司,负责公司数仓建设,试用期主要一项 OKR是制定数据仓库建设规划;因此小 A 本着从问题出发为原点,先对公司数仓现状进行一轮深入了解,理清存在问题,然后在以不忘初心原则提出解…...

容器镜像的导入导出
容器镜像的导入导出 第1关:导入导出容器 任务描述 本关任务是学习导入导出容器,要求学习者参照示例完成将busyboxContainer容器的文件系统保存为一个tar包,通过该tar包导入一个busybox:v1.0镜像。 相关知识 将 "容器的文件系统&…...

Java每日一练(20230502)
目录 1. 二叉搜索树的最近公共祖先 🌟🌟 2. 随机分组问题 🌟 3. K 个一组翻转链表 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练…...

JVM学习(九):堆
一、堆(Heap)的概述 一个JVM实例只存在一个堆内存,堆也是Java内存管理的核心区域。 Java堆区在JVM启动的时候即被创建,其空间大小也就确定了。是JVM管理的最大一块内存空间。同时,堆内存的大小是可以调节的。《Java虚拟…...
golang - switch
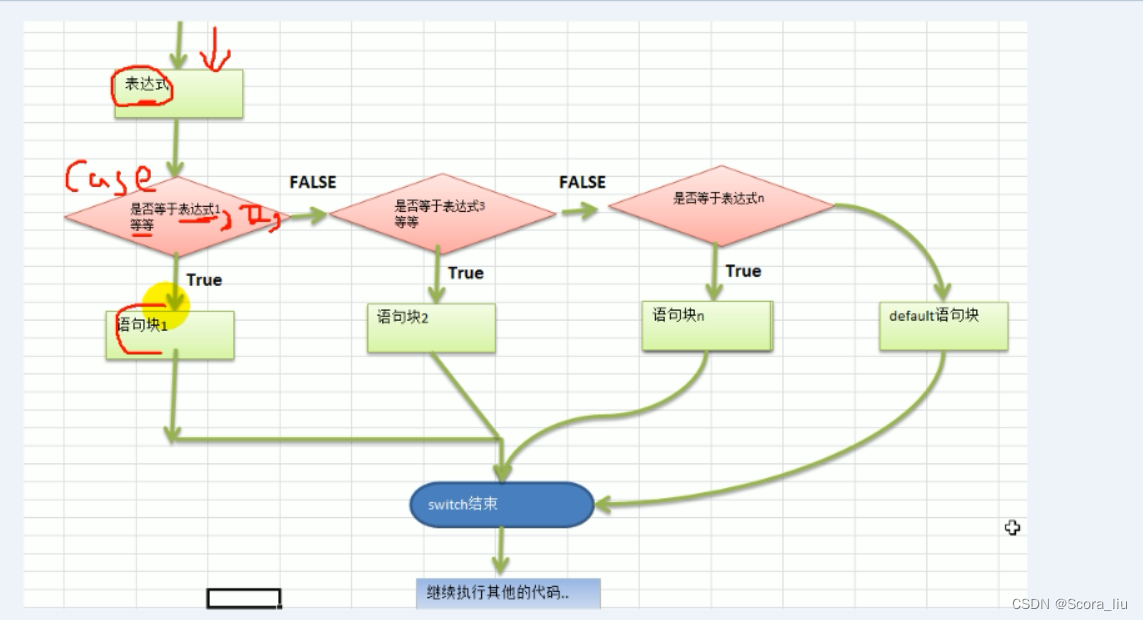
switch 的使用 switch 语句用于基于不同条件执行不同操作,,直每一个 case 分支都是唯一的,从上到下逐一测试到匹配为止匹配项后面也不需要再加 break switch 表达式 {case 表达式1, 表达式2, ... :语句块1case 表达式2, 表达式3, ... :语句块…...
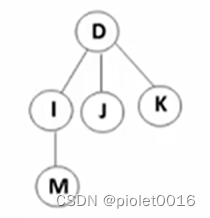
浙大数据结构与算法一些有意思的理论基础题
堆栈 有人给出了堆栈用数组实现的另一种方式,即直接在函数参数中传递数组和top变量(而不是两者组成的结构指针),其中Push操作函数设计如下。这个Push函数正确吗?为什么? #define MaxSize 100 ElementTyp…...

【热门框架】Mybatis-Plus怎样进行映射匹配兼容?Mybatis-Plus的ID有哪些生成策略
Mybatis-Plus提供了两种映射匹配兼容的方式:驼峰转下划线和全局配置。 驼峰转下划线 默认情况下,Mybatis-Plus会将Java类中的驼峰命名方式自动映射到数据库表中的下划线命名方式。例如,Java类中的userName属性会自动映射到表中的user_name字…...

Http1.0 、1.1、2.0、3.0的区别
巨人的肩膀 3.1 HTTP 常见面试题 | 小林coding HTTP1.0与HTTP1.1 HTTP1.1在HTTP1.0上的改进: 使用长连接的方式改善了HTTP1.0中短连接造成的性能开销支持管道网络传输,不必等到上一个的响应,就可以接着发送第二个请求,减少整体响…...

Python——基于YOLOV8的车牌识别(源码+教程)
目录 一、前言 二 、完成效果 三、 项目包 四、运行项目 (教程) 一、前言 YOLOv8LPRNet车牌定位与识别https://www.bilibili.com/video/BV1vk4y1E7MZ/ 最近做了有一个车牌识别的小需求,今天完成了,在此记录和分享 首先&#x…...

c# 数据保存为PDF(一) (spire pdf篇)
文章目录 前言了解 Spire使用Spire.PDF1 创建简单的PDF文档2 创建带有格式的PDF文档(使用Draw)头部信息页眉页脚测试数据完整的代码 3 创建带有格式的PDF文档(使用Gird)小结 先上一个效果图 前言 项目中需要将一些数据转存为PDF …...

Stable Diffusion使用方法
SD的本地安装教程有很多我就不重复了,这里主要是记录我在使用SD Webui的过程中遇到的问题,总结的一些提升出图效率,出好图概率的经验。 先搞几张看看效果 二次元妹妹 高达 ? Ok,以上只是一小部分成品 ,属…...
高性能:负载均衡
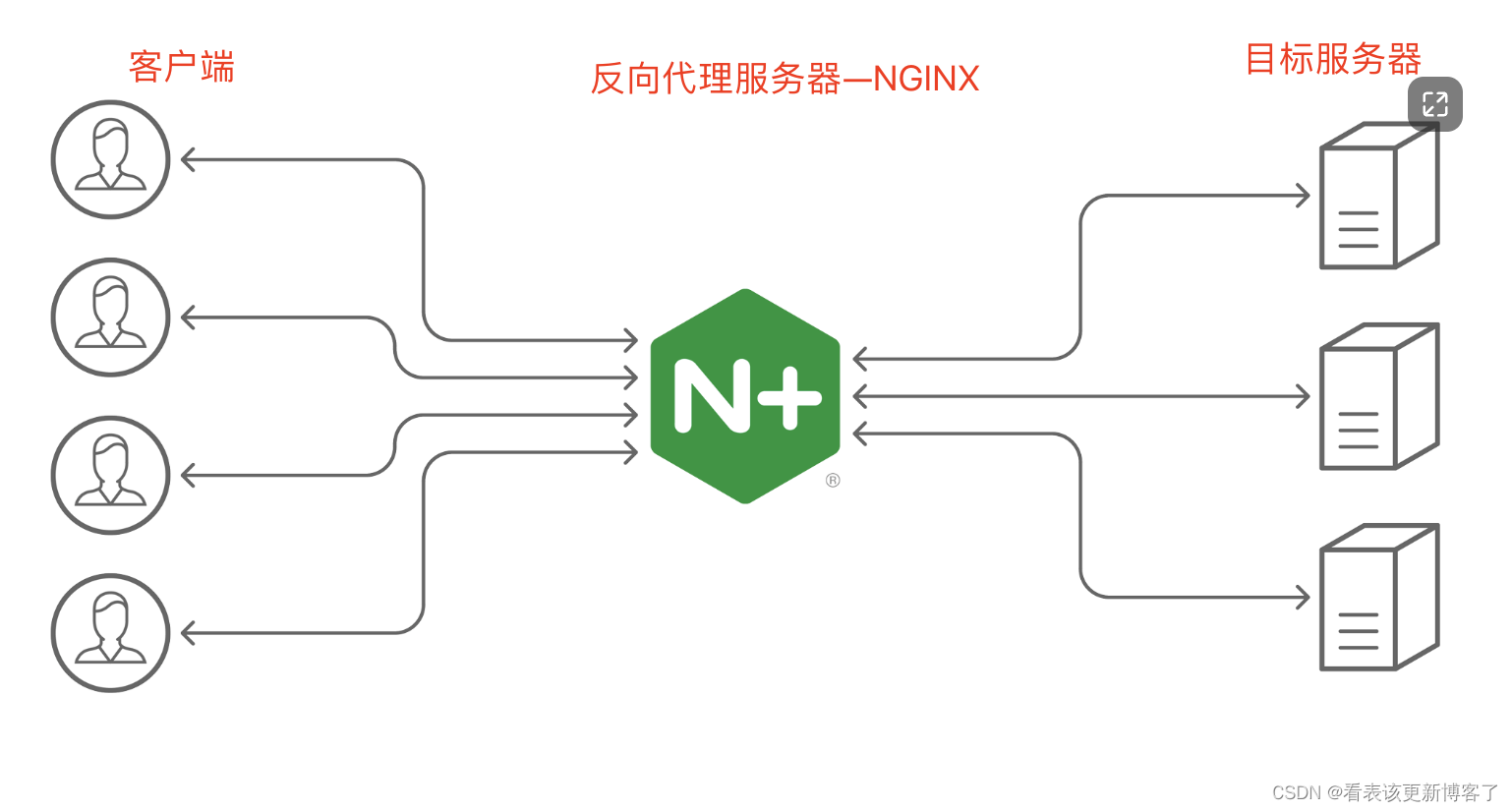
目录 什么是负载均衡 负载均衡分类 服务端负载均衡 服务端负载均衡——软硬件分类 服务端负载均衡——OSI模型分类 客户端负载均衡 负载均衡常见算法 七层负载均衡做法 DNS解析 反向代理 什么是负载均衡 将用户请求分摊(分流) 到不同的服务器上…...

Matplotlib 安装介绍
文章目录 安装步骤 Matplotlib 不止是一个数学绘图库,它也是可视化和分析工具中最流行之一。我们可用其制作简单的图表,如折线图和散点图。 安装步骤 先进入:python官网 跳转到界面: 录入并搜索 下载之前,看一下自…...

DNS:关于 DNS 基本概念的一些笔记整理
写在前面 分享一些 DNS 的笔记整理博文内容涉及: DNS 历史介绍DNS 解析顺序DNS 基本概念资源类型介绍DNS 安全 理解不足小伙伴帮忙指正 傍晚时分,你坐在屋檐下,看着天慢慢地黑下去,心里寂寞而凄凉,感到自己的生命被剥夺…...

机器人学一些知识
机器人动力学模型是用数学方法描述机器人运动和力学特性的模型。它包含机器人的几何结构、质量、惯性、摩擦等物理特性,以及机器人的控制系统和传感器等。机器人动力学模型可以用于机器人的运动规划、控制算法设计、仿真和优化等应用中。 机器人动力学模型通常采用…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
